苏教版高中数学选择性必修第一册第三章圆锥曲线与方程3.2.2双曲线的几何性质课件(共42张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第三章圆锥曲线与方程3.2.2双曲线的几何性质课件(共42张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 34.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 00:00:00 | ||
图片预览







文档简介
(共42张PPT)
苏教版2019高二数学(选修一)第三章 圆锥曲线与方程
3.2.2 双曲线的几何性质
学习目标
1.掌握双曲线的简单几何性质.(重点)
2.理解双曲线的渐近线及离心率的意义.(难点)
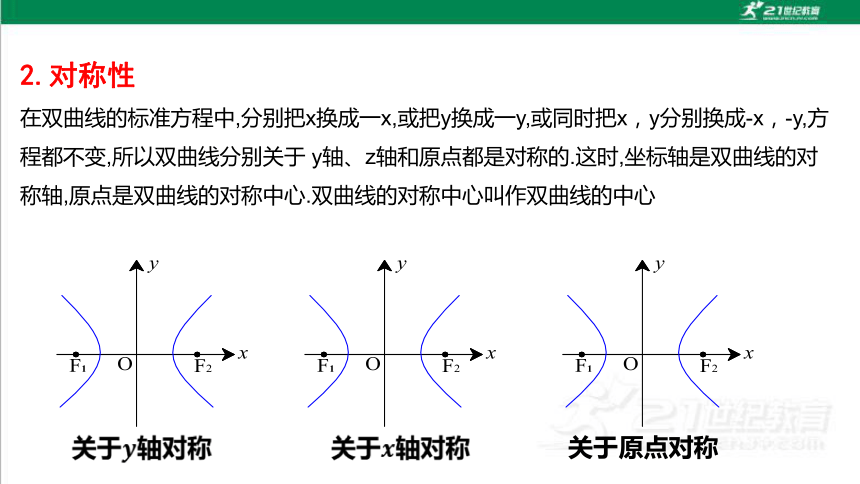
类比对椭圆几何性质的研究,你认为应该研究双曲线的哪些几何性质
如何研究这些性质
x
F1
F2
y
O
M(x,y)
F1
F2
O
x
y
A1
A2
B1
B2
新知探究
关于原点对称
2.对称性
在双曲线的标准方程中,分别把x换成一x,或把y换成一y,或同时把x,y分别换成-x,-y,方程都不变,所以双曲线分别关于 y轴、z轴和原点都是对称的.这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫作双曲线的中心
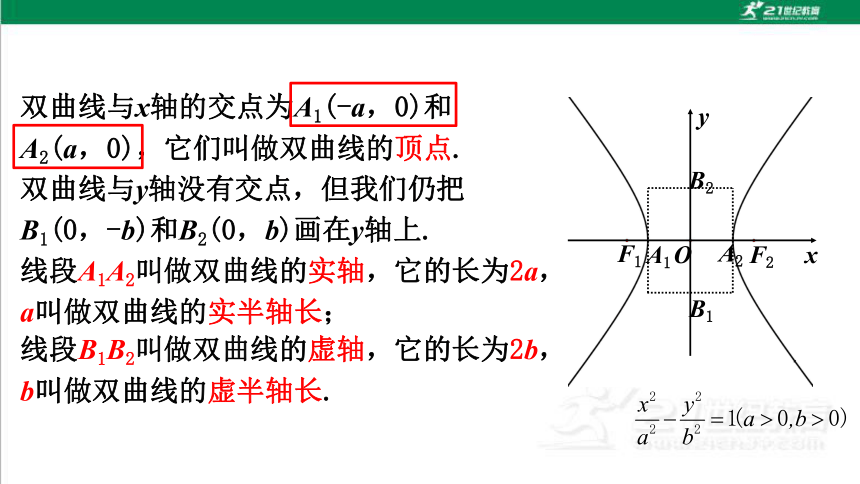
3.顶点
双曲线与x轴的交点为A1(-a,0)和A2(a,0),它们叫做双曲线的顶点.
双曲线与y轴没有交点,但我们仍把B1(0,-b)和B2(0,b)画在y轴上.
线段A1A2叫做双曲线的实轴,它的长为2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
x
O
A1
y
A2
B1
B2
F2
F1
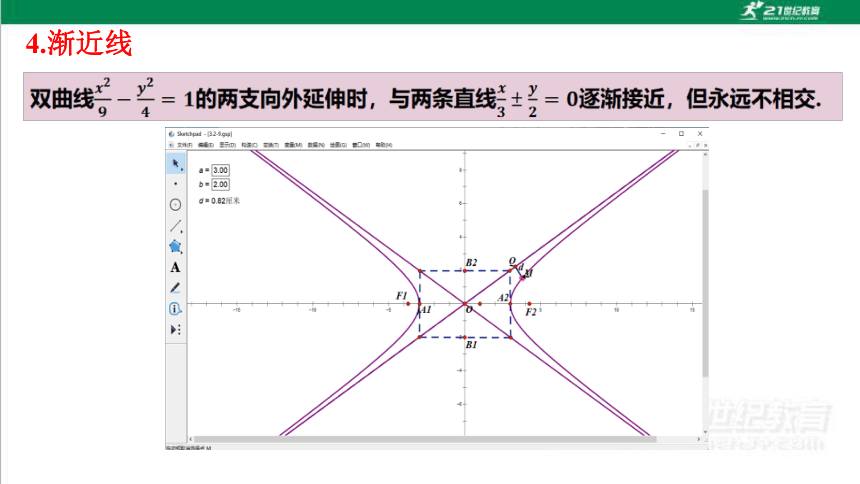
4.渐近线
双曲线的两支向外延伸时,与矩形的两条对角线逐渐接近,我们把这两条直线叫做双曲线的渐近线.
如图,直线x= a和直线y= b 围成了一个矩形,矩形的两条对角线的方程是什么?
x
O
A1
y
A2
B1
B2
F2
F1
在方程 中,如果a=b,那么双曲线的方程为x2-y2=a2,它的实轴和虚轴的长都等于2a.
这时,四条直线x =±a,y =±b围成正方形,渐近线方程为 y=±x ,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.实轴和虚轴等长的双曲线叫做等轴双曲线.
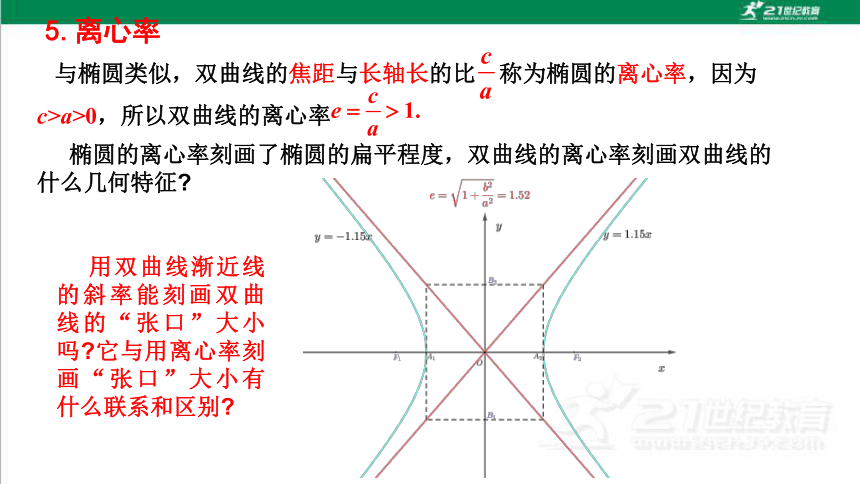
与椭圆类似,双曲线的焦距与长轴长的比 称为椭圆的离心率,因为c>a>0,所以双曲线的离心率
椭圆的离心率刻画了椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征
用双曲线渐近线的斜率能刻画双曲线的“张口”大小吗 它与用离心率刻画“张口”大小有什么联系和区别
5.离心率
课本例题
课本例题
课本练习
课本练习
A
故选:A.
课本练习
课本练习
课本练习
易错警示 求双曲线的离心率
错解分析:错误的根本原因是误以为焦点只能在x轴上,造成失解.实际上本题应该有两种情况.
防范措施:条件考虑要全面由渐近线不能确定焦点是在x轴上,还是在y轴上,因此需要分两种情况讨论.在求解圆锥曲线问题时,既要分析定量条件,又要分析定位条件,以免造成失解、错解.
题型一:由双曲线的标准方程研究其几何性质
典例剖析
归纳总结
题型二:利用几何性质求双曲线的标准方程
典例剖析
例2.求适合下列条件的椭圆的标准方程.
(2)两顶点间的距离是6,两焦点的连线被两顶点和中心四等分;
典例剖析
典例剖析
求双曲线标准方程的方法与技巧
1.根据双曲线的某些几何性质求双曲线方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.
2.巧设双曲线方程的六种方法与技巧:
(1)根据双曲线的某些几何性质求双曲线方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.
归纳总结
归纳总结
题型三:双曲线的离心率及其应用
典例剖析
归纳总结
【答案】A
随堂检测
【答案】 AD
6. (2023阳山南阳中学月考)求适合下列条件的双曲线的标准方程:
1. 根据双曲线的某些几何性质求双曲线方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.
(2) 以双曲线 有相同的渐近线的双曲线方程可设为
(1) 渐近线方程为 的双曲线方程可设为
2. 巧设双曲线方程的技巧
课堂小结
苏教版2019高二数学(选修一)第三章 圆锥曲线与方程
3.2.2 双曲线的几何性质
学习目标
1.掌握双曲线的简单几何性质.(重点)
2.理解双曲线的渐近线及离心率的意义.(难点)
类比对椭圆几何性质的研究,你认为应该研究双曲线的哪些几何性质
如何研究这些性质
x
F1
F2
y
O
M(x,y)
F1
F2
O
x
y
A1
A2
B1
B2
新知探究
关于原点对称
2.对称性
在双曲线的标准方程中,分别把x换成一x,或把y换成一y,或同时把x,y分别换成-x,-y,方程都不变,所以双曲线分别关于 y轴、z轴和原点都是对称的.这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫作双曲线的中心
3.顶点
双曲线与x轴的交点为A1(-a,0)和A2(a,0),它们叫做双曲线的顶点.
双曲线与y轴没有交点,但我们仍把B1(0,-b)和B2(0,b)画在y轴上.
线段A1A2叫做双曲线的实轴,它的长为2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
x
O
A1
y
A2
B1
B2
F2
F1
4.渐近线
双曲线的两支向外延伸时,与矩形的两条对角线逐渐接近,我们把这两条直线叫做双曲线的渐近线.
如图,直线x= a和直线y= b 围成了一个矩形,矩形的两条对角线的方程是什么?
x
O
A1
y
A2
B1
B2
F2
F1
在方程 中,如果a=b,那么双曲线的方程为x2-y2=a2,它的实轴和虚轴的长都等于2a.
这时,四条直线x =±a,y =±b围成正方形,渐近线方程为 y=±x ,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.实轴和虚轴等长的双曲线叫做等轴双曲线.
与椭圆类似,双曲线的焦距与长轴长的比 称为椭圆的离心率,因为c>a>0,所以双曲线的离心率
椭圆的离心率刻画了椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征
用双曲线渐近线的斜率能刻画双曲线的“张口”大小吗 它与用离心率刻画“张口”大小有什么联系和区别
5.离心率
课本例题
课本例题
课本练习
课本练习
A
故选:A.
课本练习
课本练习
课本练习
易错警示 求双曲线的离心率
错解分析:错误的根本原因是误以为焦点只能在x轴上,造成失解.实际上本题应该有两种情况.
防范措施:条件考虑要全面由渐近线不能确定焦点是在x轴上,还是在y轴上,因此需要分两种情况讨论.在求解圆锥曲线问题时,既要分析定量条件,又要分析定位条件,以免造成失解、错解.
题型一:由双曲线的标准方程研究其几何性质
典例剖析
归纳总结
题型二:利用几何性质求双曲线的标准方程
典例剖析
例2.求适合下列条件的椭圆的标准方程.
(2)两顶点间的距离是6,两焦点的连线被两顶点和中心四等分;
典例剖析
典例剖析
求双曲线标准方程的方法与技巧
1.根据双曲线的某些几何性质求双曲线方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.
2.巧设双曲线方程的六种方法与技巧:
(1)根据双曲线的某些几何性质求双曲线方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.
归纳总结
归纳总结
题型三:双曲线的离心率及其应用
典例剖析
归纳总结
【答案】A
随堂检测
【答案】 AD
6. (2023阳山南阳中学月考)求适合下列条件的双曲线的标准方程:
1. 根据双曲线的某些几何性质求双曲线方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.
(2) 以双曲线 有相同的渐近线的双曲线方程可设为
(1) 渐近线方程为 的双曲线方程可设为
2. 巧设双曲线方程的技巧
课堂小结
