2.2.2用样本的数字特征估计总体的数字特征
文档属性
| 名称 | 2.2.2用样本的数字特征估计总体的数字特征 |

|
|
| 格式 | zip | ||
| 文件大小 | 586.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-28 00:00:00 | ||
图片预览




文档简介
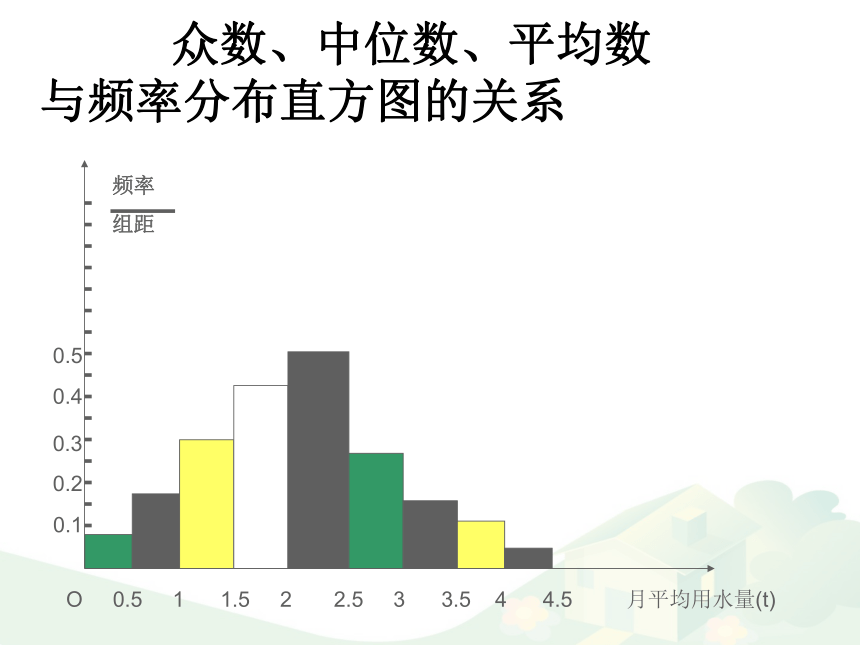
课件32张PPT。2.2.2 用样本的数字特征估计总体的数字特征复习: 众数、中位数、平均数的概念 中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数. 众数:在一组数据中,出现次数最多的数据叫做这组数据的众数. 众数、中位数、平均数与频率分布直方图的关系0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)1 众数:
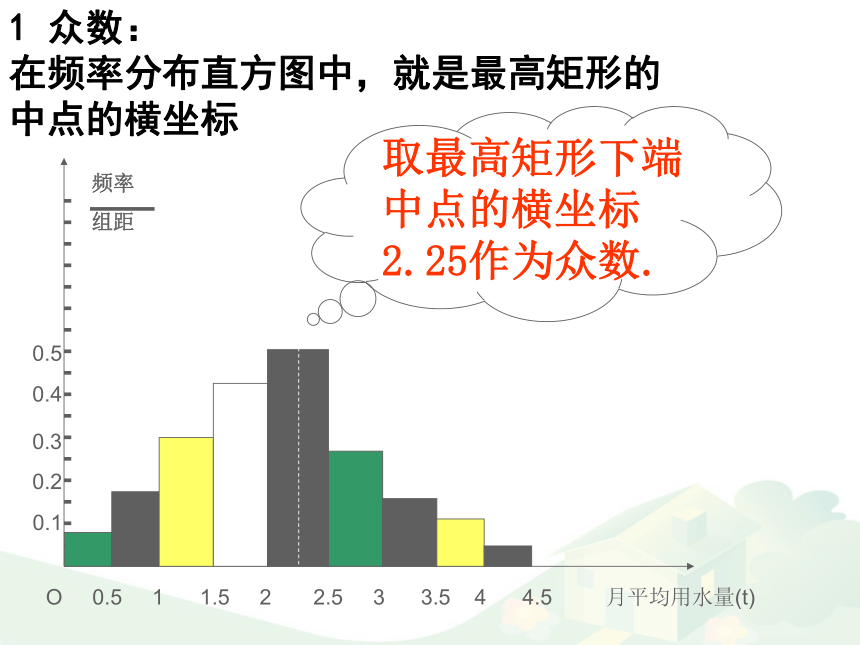
在频率分布直方图中,就是最高矩形的中点的横坐标
0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)1 众数:
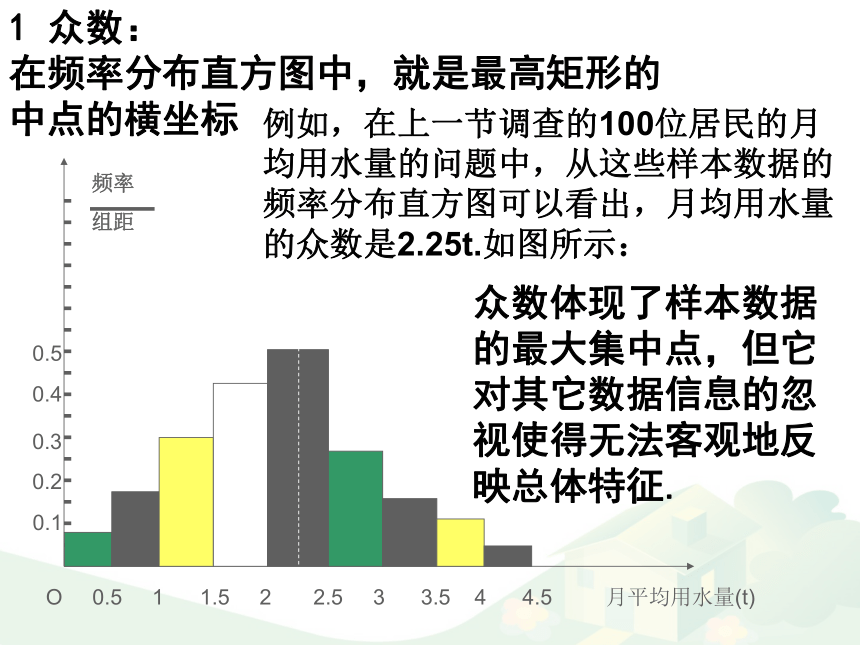
在频率分布直方图中,就是最高矩形的中点的横坐标
例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.如图所示:众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征.思考:在城市居民月均用水量样本数据的频率分布直方图中,从左至右各个小矩形的面积分别是0.04,0.08,0.15,0.22,0.25,0.14,0.06,0.04,0.02.由此估计总体的中位数是什么? 2 中位数
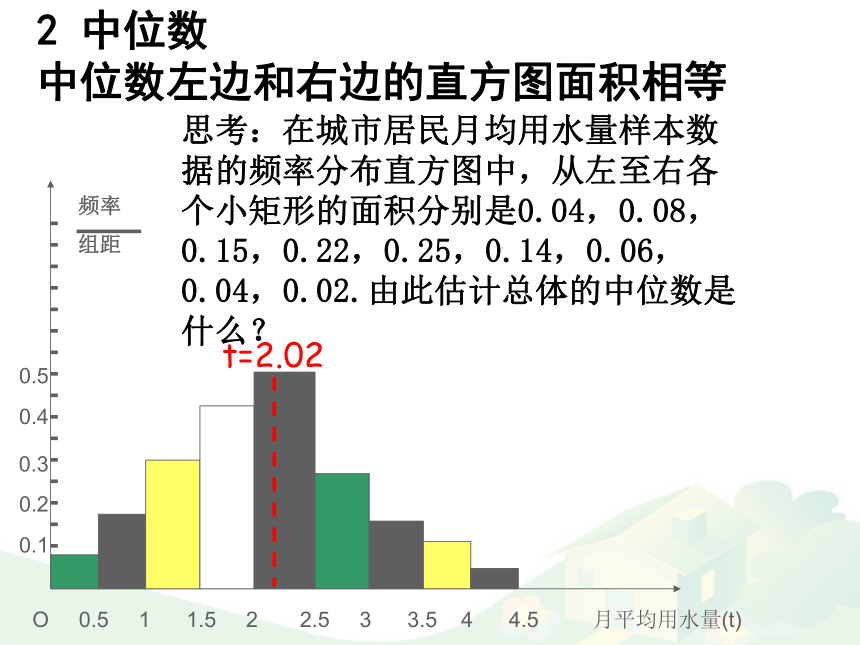
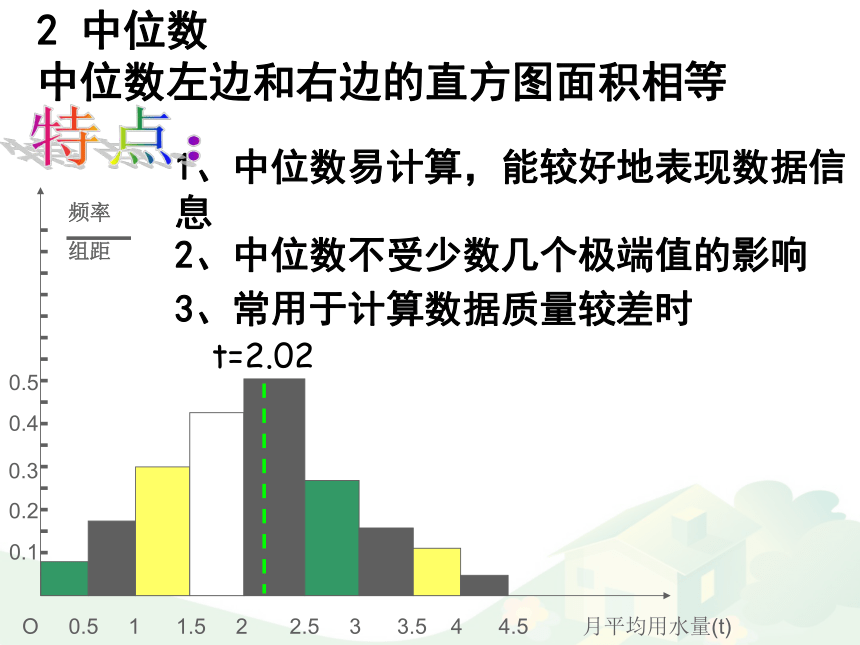
中位数左边和右边的直方图面积相等t=2.022 中位数
中位数左边和右边的直方图面积相等2.02这个中位数的估计值,与样本的中位数值2.0不一样,为什么?因为频率分布直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致.t=2.022 中位数
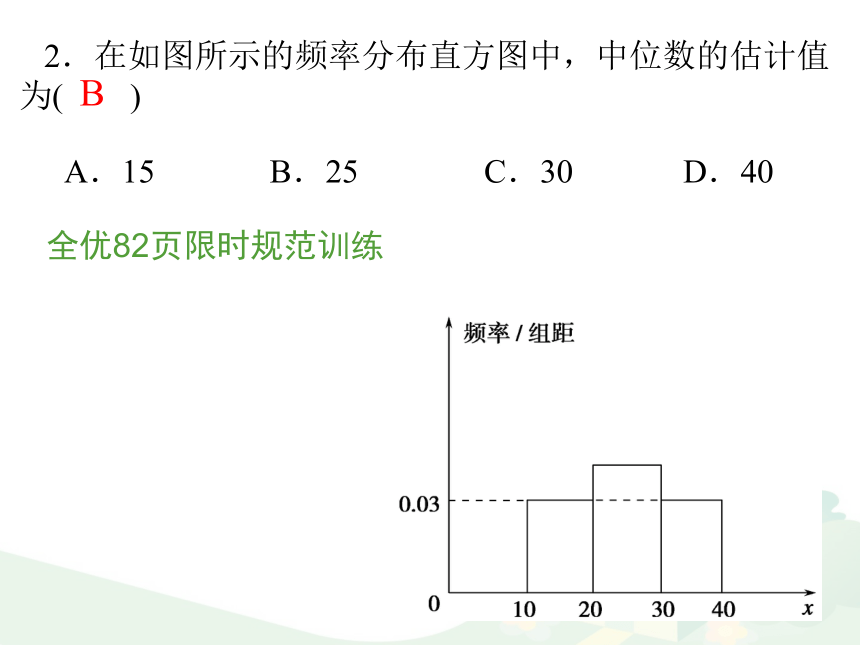
中位数左边和右边的直方图面积相等t=2.022、中位数不受少数几个极端值的影响1、中位数易计算,能较好地表现数据信息3、常用于计算数据质量较差时特点:2.在如图所示的频率分布直方图中,中位数的估计值为( )A.15 B.25 C.30 D.40B全优82页限时规范训练3 平均数
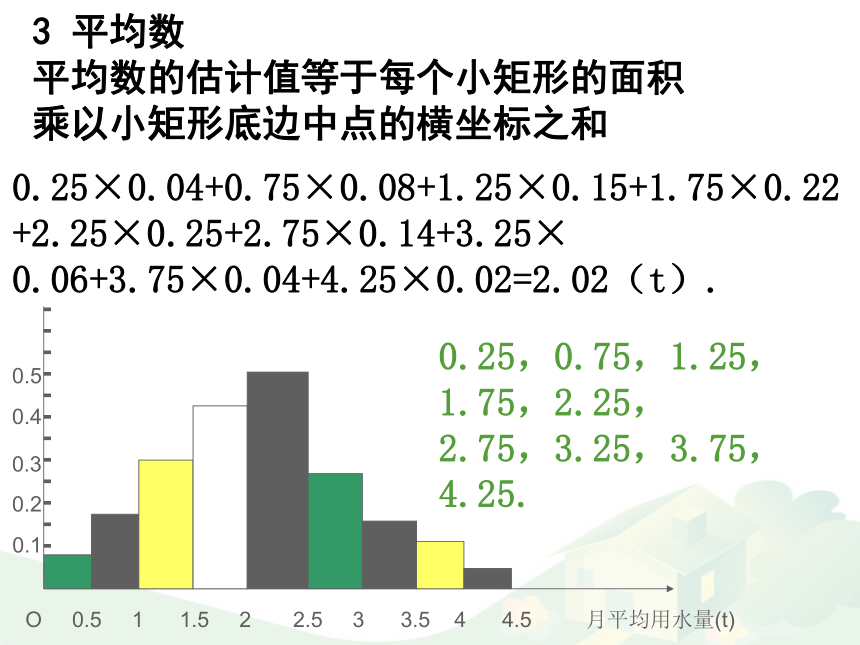
平均数的估计值等于每个小矩形的面积
乘以小矩形底边中点的横坐标之和0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25× 0.06+3.75×0.04+4.25×0.02=2.02(t). 0.25,0.75,1.25,1.75,2.25,
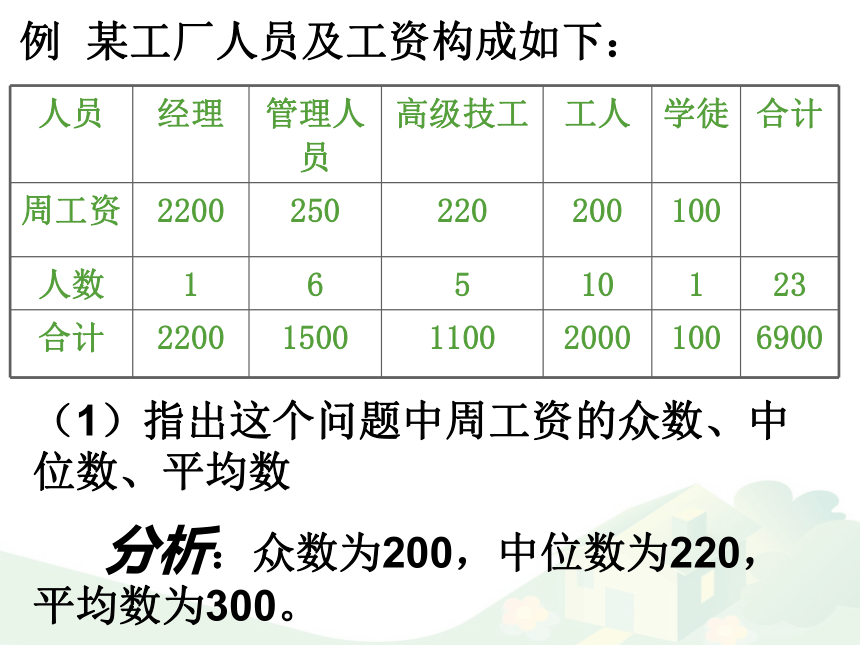
2.75,3.25,3.75,4.25. 是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点横坐标之和3、平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。1、平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变2、平均数可以反映出更多的关于样本数据全体的信息特点:平均数例 某工厂人员及工资构成如下:(1)指出这个问题中周工资的众数、中位数、平均数 分析:众数为200,中位数为220,平均数为300。因平均数为300,由表格中所列出的数据
可见,只有经理在平均数以上,其余的人
都在平均数以下,故用平均数不能客观真
实地反映该工厂的工资水平。(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么?答案:D全优43页基础夯实6.(2013年重庆)以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分)
已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )
A.2,5 B.5,5 C.5,8 D.8,8全优44页能力提升【解析】乙组数据平均数C∴y=8.甲组数据可排列为9,12,10+x,24,27,中位数为10+x=15,∴x=5.3.(2013年上海)某学校高一年级男生人数占该年级学生人数的40%,在一次考试中,男,女平均分数分别为75、80,则这次考试该年级学生平均分数为______.78【解析】设该年级有学生x人,则男生有40%x人,女生有60%x人,这次考试该年级学生平均分数为a,根据题意,得75×40%x+80×60%x=xa,解得a=78.故这次考试该年级学生平均分数为78.全优82页限时规范训练在一次射击比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,8,10,7,4;
乙运动员﹕9,5,7,8,7,6,8,6,7,7.
观察上述样本数据,你能判断哪个运动员发挥的更稳定些吗? 两个人射击的平均成绩是一样的。那么,是否两个人就没有水平差距呢?发现:反映样本数据的分散程度的大小,最常用的统计量是标准差,一般用s表示.样本数据的标准差的算法:1、算出样本数据的平均数。
2、算出每个样本数据与样本数据平均数的差
3、算出n个平方数的平均数,即为样本方差。
4、算出平均数的算术平方根,,即为样本标准差。
5、其计算公式为:标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小。
标准差的取值范围是什么?标准差为0的样本数据有什么特点?
当 时,意味着所有的样本数据都等于样本平均数。人们有时用标准差的平方(即方差)来代替标准差,作为测量样本数据分散程度的工具:方差
从数学的角度考虑,人们有时用标准差的平方(即方差)来代替标准差,作为测量样本数据分散程度的工具:
在刻画样本数据的分散程度上,方差和标准差是一样的,但在解决实际问题时,一般多采用标准差.〖例1〗:画出下列四组样本数据的直方图,说明他们的异同点。
(1)5,5,5,5,5,5,5,5,5
(2)4,4,4,5,5,5,6,6,6
(3)3,3,4,4,5,6,6,7,7
(4)2,2,2,2,5,8,8,8,8分析:先画出数据的直方图,根据样本数据算出样本数据的平均数,利用标准差的计算公式即可算出每一组数据的标准差。见课本76页例题图
四组数据的平均数都是5.0,标准差分别为:0.00,0.82,1.49,2.83。
他们有相同的平均数,但他们有不同的标准差,说明数据的分散程度是不一样的。4.从一堆苹果中任取5只,称得它们的质量如下(单位:克)125,124,121,123,127,则该样本标准差s=________(克)(用数字作答).2【解析】[(125-124)2+(124-124)2+(121-124)2+(123-124)2+(127-124)2]=4,s=2.全优82页限时规范训练5.随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差.【解析】(1)乙班的平均身高较高.(2)因为甲班的平均身高为所以甲班的样本方差(2×122+2×92+2×22+12+72+82+02)=57.2.全优82页限时规范训练8.(2014年新课标Ⅰ)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:(1)在下图中作出这些数据的频率分布直方图:全优44页能力提升【解析】(1)如图.8.(2014年新课标Ⅰ)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);【解析】(2)质量指标值的样本平均数为80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.质量指标值的样本方差为(-20)2×0.06+(-10)2×0.26+0×0.38+(10)2×0.22+(20)2×0.08=104.8.(2014年新课标Ⅰ)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:【解析】(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.由于该估计值小于0.8,故不能认为该企业生产的这种产品“质量指标值不低于95的产品至少要占全部产品80%”的规定.解析 设这40个数据为x1,x2,…,x40,
则S2=全优44页基础夯实2.为了让人们感受到丢弃塑料袋对环境造成的影响,某班环保小组的6名同学记录了自己家中一周内(一周按6天计算)丢弃的塑料袋的数量,结果如下(单位:个):33,25,28,26,25,31.如果该班有45名同学,那么根据提供的数据估计,本周全班同学的家庭总共丢弃塑料袋的数量约为( )
A.900个 B.1080个 C.1260个 D.1800个全优43页基础夯实1.期中考试以后,班长算出了全班40个人数学成绩的平均分为M,如果把M当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为N,那么M:N为( )
A.40∶41 B.1 C.41∶40 D.2解析:∵全班40个人数学成绩的平均分为M,把M当成一个同学的分数,则班中有41名同学总分为40M+M=41M,∴M:N=1全优82页限时规范训练
在频率分布直方图中,就是最高矩形的中点的横坐标
0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)1 众数:
在频率分布直方图中,就是最高矩形的中点的横坐标
例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.如图所示:众数体现了样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征.思考:在城市居民月均用水量样本数据的频率分布直方图中,从左至右各个小矩形的面积分别是0.04,0.08,0.15,0.22,0.25,0.14,0.06,0.04,0.02.由此估计总体的中位数是什么? 2 中位数
中位数左边和右边的直方图面积相等t=2.022 中位数
中位数左边和右边的直方图面积相等2.02这个中位数的估计值,与样本的中位数值2.0不一样,为什么?因为频率分布直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致.t=2.022 中位数
中位数左边和右边的直方图面积相等t=2.022、中位数不受少数几个极端值的影响1、中位数易计算,能较好地表现数据信息3、常用于计算数据质量较差时特点:2.在如图所示的频率分布直方图中,中位数的估计值为( )A.15 B.25 C.30 D.40B全优82页限时规范训练3 平均数
平均数的估计值等于每个小矩形的面积
乘以小矩形底边中点的横坐标之和0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25× 0.06+3.75×0.04+4.25×0.02=2.02(t). 0.25,0.75,1.25,1.75,2.25,
2.75,3.25,3.75,4.25. 是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点横坐标之和3、平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。1、平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变2、平均数可以反映出更多的关于样本数据全体的信息特点:平均数例 某工厂人员及工资构成如下:(1)指出这个问题中周工资的众数、中位数、平均数 分析:众数为200,中位数为220,平均数为300。因平均数为300,由表格中所列出的数据
可见,只有经理在平均数以上,其余的人
都在平均数以下,故用平均数不能客观真
实地反映该工厂的工资水平。(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么?答案:D全优43页基础夯实6.(2013年重庆)以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分)
已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )
A.2,5 B.5,5 C.5,8 D.8,8全优44页能力提升【解析】乙组数据平均数C∴y=8.甲组数据可排列为9,12,10+x,24,27,中位数为10+x=15,∴x=5.3.(2013年上海)某学校高一年级男生人数占该年级学生人数的40%,在一次考试中,男,女平均分数分别为75、80,则这次考试该年级学生平均分数为______.78【解析】设该年级有学生x人,则男生有40%x人,女生有60%x人,这次考试该年级学生平均分数为a,根据题意,得75×40%x+80×60%x=xa,解得a=78.故这次考试该年级学生平均分数为78.全优82页限时规范训练在一次射击比赛中,甲、乙两名运动员各射击10次,命中环数如下﹕
甲运动员﹕7,8,6,8,6,5,8,10,7,4;
乙运动员﹕9,5,7,8,7,6,8,6,7,7.
观察上述样本数据,你能判断哪个运动员发挥的更稳定些吗? 两个人射击的平均成绩是一样的。那么,是否两个人就没有水平差距呢?发现:反映样本数据的分散程度的大小,最常用的统计量是标准差,一般用s表示.样本数据的标准差的算法:1、算出样本数据的平均数。
2、算出每个样本数据与样本数据平均数的差
3、算出n个平方数的平均数,即为样本方差。
4、算出平均数的算术平方根,,即为样本标准差。
5、其计算公式为:标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小。
标准差的取值范围是什么?标准差为0的样本数据有什么特点?
当 时,意味着所有的样本数据都等于样本平均数。人们有时用标准差的平方(即方差)来代替标准差,作为测量样本数据分散程度的工具:方差
从数学的角度考虑,人们有时用标准差的平方(即方差)来代替标准差,作为测量样本数据分散程度的工具:
在刻画样本数据的分散程度上,方差和标准差是一样的,但在解决实际问题时,一般多采用标准差.〖例1〗:画出下列四组样本数据的直方图,说明他们的异同点。
(1)5,5,5,5,5,5,5,5,5
(2)4,4,4,5,5,5,6,6,6
(3)3,3,4,4,5,6,6,7,7
(4)2,2,2,2,5,8,8,8,8分析:先画出数据的直方图,根据样本数据算出样本数据的平均数,利用标准差的计算公式即可算出每一组数据的标准差。见课本76页例题图
四组数据的平均数都是5.0,标准差分别为:0.00,0.82,1.49,2.83。
他们有相同的平均数,但他们有不同的标准差,说明数据的分散程度是不一样的。4.从一堆苹果中任取5只,称得它们的质量如下(单位:克)125,124,121,123,127,则该样本标准差s=________(克)(用数字作答).2【解析】[(125-124)2+(124-124)2+(121-124)2+(123-124)2+(127-124)2]=4,s=2.全优82页限时规范训练5.随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差.【解析】(1)乙班的平均身高较高.(2)因为甲班的平均身高为所以甲班的样本方差(2×122+2×92+2×22+12+72+82+02)=57.2.全优82页限时规范训练8.(2014年新课标Ⅰ)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:(1)在下图中作出这些数据的频率分布直方图:全优44页能力提升【解析】(1)如图.8.(2014年新课标Ⅰ)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);【解析】(2)质量指标值的样本平均数为80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.质量指标值的样本方差为(-20)2×0.06+(-10)2×0.26+0×0.38+(10)2×0.22+(20)2×0.08=104.8.(2014年新课标Ⅰ)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:【解析】(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.由于该估计值小于0.8,故不能认为该企业生产的这种产品“质量指标值不低于95的产品至少要占全部产品80%”的规定.解析 设这40个数据为x1,x2,…,x40,
则S2=全优44页基础夯实2.为了让人们感受到丢弃塑料袋对环境造成的影响,某班环保小组的6名同学记录了自己家中一周内(一周按6天计算)丢弃的塑料袋的数量,结果如下(单位:个):33,25,28,26,25,31.如果该班有45名同学,那么根据提供的数据估计,本周全班同学的家庭总共丢弃塑料袋的数量约为( )
A.900个 B.1080个 C.1260个 D.1800个全优43页基础夯实1.期中考试以后,班长算出了全班40个人数学成绩的平均分为M,如果把M当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为N,那么M:N为( )
A.40∶41 B.1 C.41∶40 D.2解析:∵全班40个人数学成绩的平均分为M,把M当成一个同学的分数,则班中有41名同学总分为40M+M=41M,∴M:N=1全优82页限时规范训练
