8.3.1完全平方公式课件(30张PPT)初中数学沪科版(2024)七年级下册
文档属性
| 名称 | 8.3.1完全平方公式课件(30张PPT)初中数学沪科版(2024)七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 347.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 08:51:44 | ||
图片预览











文档简介
(共30张PPT)
8.3.1 完全平方公式
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式的乘法法则:
知识回顾
知识回顾
单项式与多项式的乘法法则:
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
n(a+b+c)
=na+nb+nc
多项式与多项式的乘法法则:
再把所得的积相加.
多项式与多项式相乘,
与另一个多项式的每一项相乘,
先用一个多项式的每一项
(a+b)(m+n) =
2
an
bm
bn
1
3
4
am
1
2
3
4
+
+
+
知识回顾
问题 1 有一个边长为 a 的正方形广场,现要扩建该广场,要求将其边长增加 b,试问扩建后这个正方形广场的面积有多大?
b
a
a
b
方法一:扩大后正方形广场的边长是 ,所以它的面积是 .
(a+b)2
方法二:先算 4 块小图形形的面积,再求总面积,扩大后正方形广场的面积是 .
因此,有
(a+b)2 = a2+2ab+b2
a+b
(a+b)2
a2
ab
b2
ab
a2+2ab+b2
(a+b)2=a2+2ab+b2
你能用多项式与多项式的乘法法则来说明它成立吗
(a+b)2 =
(a+b)
(a+b)
=a2+ab
+ab+b2
=a2+2ab+b2
创设情境
这两个数乘积的 2 倍.
式子的左边为两个数的和的平方;
(a+b)2=a2+2ab+b2
思考:(1)式子的左边具有什么特征?
(2)运算的结果有什么特征呢?
结果为
创设情境
这两个数的平方和
加
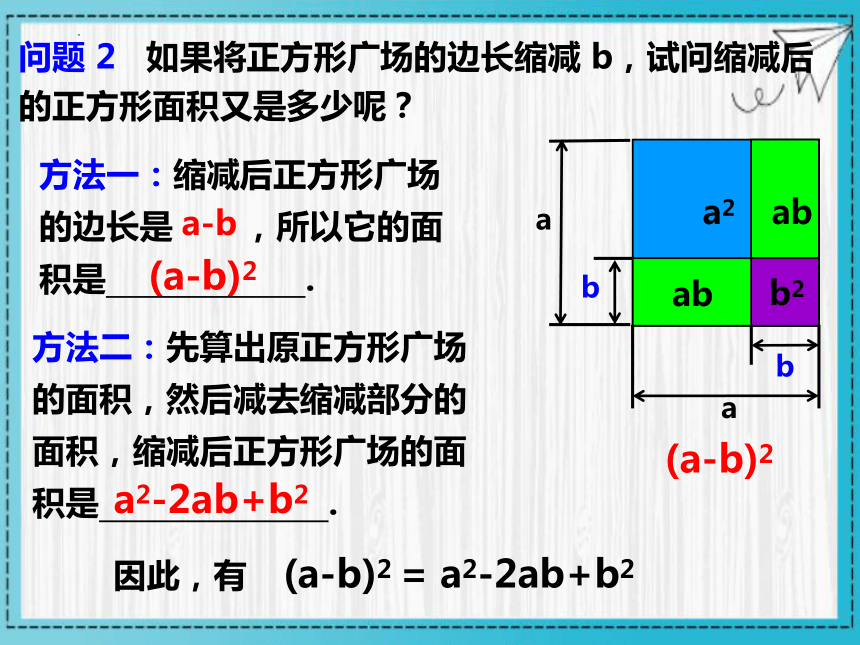
问题 2 如果将正方形广场的边长缩减 b,试问缩减后的正方形面积又是多少呢?
方法一:缩减后正方形广场的边长是 ,所以它的面积是 .
(a-b)2
方法二:先算出原正方形广场的面积,然后减去缩减部分的面积,缩减后正方形广场的面积是 .
a2-2ab+b2
因此,有
(a-b)2 = a2-2ab+b2
b
a
a
b
a-b
(a-b)2
a2
ab
b2
ab
(a-b)2=a2-2ab+b2
你能用多项式与多项式的乘法法则来说明它成立吗
创设情境
(a-b)2 =
(a-b)
(a-b)
=a2-ab
-ab+b2
=a2-2ab+b2
(a-b)2=a2-2ab+b2
思考:(1)式子的左边具有什么特征?
式子的左边为两个数的差的平方;
(2)运算的结果有什么特征呢?
创设情境
这两个数乘积的 2 倍.
结果为
这两个数的平方和
减
归纳总结
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
①
②
同学们,你能用语言叙述这两个等式吗?
两个数的和(或差)的平方,
这两个数乘积的 2 倍.
等于
这两个数的平方和
加
(或减)
上面两个等式,作为公式可以直接应用于运算,称为完全平方公式
口诀:
首平方,尾平方,乘积的 2 倍放中央,符号看前方.
问题 3 观察下面两个完全平方公式,比一比, 回答下列问题:
1、说一说积的次数和项数.
2、两个完全平方公式的积有相同的项吗 与a, b有什么关系?
3、两个完全平方公式的积中不同的是哪一项 与 a,b 有什么关系?它的符号与什么有关?
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
①
②
积为二次三项式
积中相同的两项为两数的平方和
不同的一项是两数积的 2 倍,
且与两数中间的符号相同.
拓展提高
公式中的字母 a,b 可以表示具体的数,也可以表示单项式或多项式.
例 1 利用乘法公式计算:
(1) (2x+y)2
运用公式计算,要先识别 a,b 在具体式子中分别表示什么.
解:(2x+y)2=
( )2=
a2 + 2 ab + b2
(2x)2
2 2x y
+
y2
+
= 4x2+4xy+y2
a
+
b
(2) (3a-2b)2
解:(3a-2b)2=
( )2=
a2 - 2 ab + b2
(3a)2
2 3a 2b
-
(2b)2
+
= 9a2-12ab+4b2
方法一:
a
-
b
例 2 利用乘法公式计算:
(2) (3a-2b)2
解:原式=
[3a+(-2b)]2
2 3a (-2b)
(-2b)2
+
= 9a2
-12ab
+4b2
方法二:
=(3a)2
+
例 2 利用乘法公式计算:
巩固练习
1、利用乘法公式计算:
(1) (3x+1)2
解:(3x+1)2=
( )2=
a2 + 2 ab + b2
(3x)2
2 3x 1
+
12
+
= 9x2+6x+1
a
+
b
(2)
解: =
( )2=
a2 - 2 ab + b2
a
-
b
y2
-
2 y
1
2
+
=
y2-y+
1
4
利用完全平方公式进行整式运算的基本步骤:
归纳总结
① 确定公式中的 a,b
② 确定和差关系
③ 选择公式
④ 计算结果
巩固练习
2、利用乘法公式计算:
(1) (-2x+3y)2
方法一:
解:原式=
2 (-2x) 3y
(3y)2
+
= 4x2
-12xy
+9y2
(-2x)2
+
巩固练习
方法二:
(1) (-2x+3y)2
解:原式=
(3y-2x)2
2 3y 2x
(2x)2
+
=9y2
-12xy
+4x2
= (3y)2
-
2、利用乘法公式计算:
巩固练习
(2) (-3m-4n)2
方法一:
解:原式=
2 3m 4n
(4n)2
+
=(3m)2
+
[-(3m+4n)]2
= (3m+4n)2
= 9m2
+24mn
+16n2
2、利用乘法公式计算:
巩固练习
(2) (-3m-4n)2
方法二:
解:原式=
2 (-3m) (-4n)
(-4n)2
+
=(-3m)2
+
[(-3m)+(-4n)]2
=9m2
+24mn
+16n2
2、利用乘法公式计算:
巩固练习
(2) (-3m-4n)2
方法三:
解:原式=
2 (-3m) 4n
(4n)2
+
=(-3m)2
-
[(-3m)-4n]2
=9m2
+24mn
+16n2
2、利用乘法公式计算:
巩固练习
(3) (x2-2y2)2
解:原式=
2 x2 2y2
(2y2)2
+
(x2)2
-
=x4
- 4x2y2
+4y4
2、利用乘法公式计算:
巩固练习
2、利用完全平方公式简便计算:
(4) 5022
(5) 4992
一个数的平方,可以考虑变形为“两数和(差)的平方”的形式.
拓展提高
巩固练习
3、下列各式中能用完全平方公式计算的是( )
A.(2a-3b)(-2a-3b) B.(2a-3b)(2a+3b)
C.(2a-3b)(-2a+3b) D.(2a-3b)(2b-3a)
C
巩固练习
4、计算:
(1) ( )2=4x2-12xy+9y2
(2) (x )2=x2-x+
1
4
2x-3y
-
1
2
提高练习
5、计算:
(1) (a+b+c)2
解:原式=
2 (a+b) c
c2
+
=a2+2ab+b2+2ac+2bc+c2
=(a+b)2
+
[(a+b)+c]2
=a2+b2+c2+2ab+2ac+2bc
拓展提高
公式中的字母 a,b 可以表示具体的数,也可以表示单项式或多项式.
巩固练习
6、计算:
(1) (a+2b)2-(a-2b)2
(2) (2x-1)(x+2)-(x-2)2-(x+2)2
(2) (2x-1)(x+2)-(x-2)2-(x+2)2
本节课你有什么收获?
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
①
②
完全平方公式
口诀:
首平方,尾平方,乘积的 2 倍放中央,符号看前方.
完全平方公式用语言叙述是:
两个数的和(或差)的平方,
这两个数乘积的 2 倍.
等于
这两个数的平方和
加
(或减)
8.3.1 完全平方公式
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式的乘法法则:
知识回顾
知识回顾
单项式与多项式的乘法法则:
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
n(a+b+c)
=na+nb+nc
多项式与多项式的乘法法则:
再把所得的积相加.
多项式与多项式相乘,
与另一个多项式的每一项相乘,
先用一个多项式的每一项
(a+b)(m+n) =
2
an
bm
bn
1
3
4
am
1
2
3
4
+
+
+
知识回顾
问题 1 有一个边长为 a 的正方形广场,现要扩建该广场,要求将其边长增加 b,试问扩建后这个正方形广场的面积有多大?
b
a
a
b
方法一:扩大后正方形广场的边长是 ,所以它的面积是 .
(a+b)2
方法二:先算 4 块小图形形的面积,再求总面积,扩大后正方形广场的面积是 .
因此,有
(a+b)2 = a2+2ab+b2
a+b
(a+b)2
a2
ab
b2
ab
a2+2ab+b2
(a+b)2=a2+2ab+b2
你能用多项式与多项式的乘法法则来说明它成立吗
(a+b)2 =
(a+b)
(a+b)
=a2+ab
+ab+b2
=a2+2ab+b2
创设情境
这两个数乘积的 2 倍.
式子的左边为两个数的和的平方;
(a+b)2=a2+2ab+b2
思考:(1)式子的左边具有什么特征?
(2)运算的结果有什么特征呢?
结果为
创设情境
这两个数的平方和
加
问题 2 如果将正方形广场的边长缩减 b,试问缩减后的正方形面积又是多少呢?
方法一:缩减后正方形广场的边长是 ,所以它的面积是 .
(a-b)2
方法二:先算出原正方形广场的面积,然后减去缩减部分的面积,缩减后正方形广场的面积是 .
a2-2ab+b2
因此,有
(a-b)2 = a2-2ab+b2
b
a
a
b
a-b
(a-b)2
a2
ab
b2
ab
(a-b)2=a2-2ab+b2
你能用多项式与多项式的乘法法则来说明它成立吗
创设情境
(a-b)2 =
(a-b)
(a-b)
=a2-ab
-ab+b2
=a2-2ab+b2
(a-b)2=a2-2ab+b2
思考:(1)式子的左边具有什么特征?
式子的左边为两个数的差的平方;
(2)运算的结果有什么特征呢?
创设情境
这两个数乘积的 2 倍.
结果为
这两个数的平方和
减
归纳总结
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
①
②
同学们,你能用语言叙述这两个等式吗?
两个数的和(或差)的平方,
这两个数乘积的 2 倍.
等于
这两个数的平方和
加
(或减)
上面两个等式,作为公式可以直接应用于运算,称为完全平方公式
口诀:
首平方,尾平方,乘积的 2 倍放中央,符号看前方.
问题 3 观察下面两个完全平方公式,比一比, 回答下列问题:
1、说一说积的次数和项数.
2、两个完全平方公式的积有相同的项吗 与a, b有什么关系?
3、两个完全平方公式的积中不同的是哪一项 与 a,b 有什么关系?它的符号与什么有关?
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
①
②
积为二次三项式
积中相同的两项为两数的平方和
不同的一项是两数积的 2 倍,
且与两数中间的符号相同.
拓展提高
公式中的字母 a,b 可以表示具体的数,也可以表示单项式或多项式.
例 1 利用乘法公式计算:
(1) (2x+y)2
运用公式计算,要先识别 a,b 在具体式子中分别表示什么.
解:(2x+y)2=
( )2=
a2 + 2 ab + b2
(2x)2
2 2x y
+
y2
+
= 4x2+4xy+y2
a
+
b
(2) (3a-2b)2
解:(3a-2b)2=
( )2=
a2 - 2 ab + b2
(3a)2
2 3a 2b
-
(2b)2
+
= 9a2-12ab+4b2
方法一:
a
-
b
例 2 利用乘法公式计算:
(2) (3a-2b)2
解:原式=
[3a+(-2b)]2
2 3a (-2b)
(-2b)2
+
= 9a2
-12ab
+4b2
方法二:
=(3a)2
+
例 2 利用乘法公式计算:
巩固练习
1、利用乘法公式计算:
(1) (3x+1)2
解:(3x+1)2=
( )2=
a2 + 2 ab + b2
(3x)2
2 3x 1
+
12
+
= 9x2+6x+1
a
+
b
(2)
解: =
( )2=
a2 - 2 ab + b2
a
-
b
y2
-
2 y
1
2
+
=
y2-y+
1
4
利用完全平方公式进行整式运算的基本步骤:
归纳总结
① 确定公式中的 a,b
② 确定和差关系
③ 选择公式
④ 计算结果
巩固练习
2、利用乘法公式计算:
(1) (-2x+3y)2
方法一:
解:原式=
2 (-2x) 3y
(3y)2
+
= 4x2
-12xy
+9y2
(-2x)2
+
巩固练习
方法二:
(1) (-2x+3y)2
解:原式=
(3y-2x)2
2 3y 2x
(2x)2
+
=9y2
-12xy
+4x2
= (3y)2
-
2、利用乘法公式计算:
巩固练习
(2) (-3m-4n)2
方法一:
解:原式=
2 3m 4n
(4n)2
+
=(3m)2
+
[-(3m+4n)]2
= (3m+4n)2
= 9m2
+24mn
+16n2
2、利用乘法公式计算:
巩固练习
(2) (-3m-4n)2
方法二:
解:原式=
2 (-3m) (-4n)
(-4n)2
+
=(-3m)2
+
[(-3m)+(-4n)]2
=9m2
+24mn
+16n2
2、利用乘法公式计算:
巩固练习
(2) (-3m-4n)2
方法三:
解:原式=
2 (-3m) 4n
(4n)2
+
=(-3m)2
-
[(-3m)-4n]2
=9m2
+24mn
+16n2
2、利用乘法公式计算:
巩固练习
(3) (x2-2y2)2
解:原式=
2 x2 2y2
(2y2)2
+
(x2)2
-
=x4
- 4x2y2
+4y4
2、利用乘法公式计算:
巩固练习
2、利用完全平方公式简便计算:
(4) 5022
(5) 4992
一个数的平方,可以考虑变形为“两数和(差)的平方”的形式.
拓展提高
巩固练习
3、下列各式中能用完全平方公式计算的是( )
A.(2a-3b)(-2a-3b) B.(2a-3b)(2a+3b)
C.(2a-3b)(-2a+3b) D.(2a-3b)(2b-3a)
C
巩固练习
4、计算:
(1) ( )2=4x2-12xy+9y2
(2) (x )2=x2-x+
1
4
2x-3y
-
1
2
提高练习
5、计算:
(1) (a+b+c)2
解:原式=
2 (a+b) c
c2
+
=a2+2ab+b2+2ac+2bc+c2
=(a+b)2
+
[(a+b)+c]2
=a2+b2+c2+2ab+2ac+2bc
拓展提高
公式中的字母 a,b 可以表示具体的数,也可以表示单项式或多项式.
巩固练习
6、计算:
(1) (a+2b)2-(a-2b)2
(2) (2x-1)(x+2)-(x-2)2-(x+2)2
(2) (2x-1)(x+2)-(x-2)2-(x+2)2
本节课你有什么收获?
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
①
②
完全平方公式
口诀:
首平方,尾平方,乘积的 2 倍放中央,符号看前方.
完全平方公式用语言叙述是:
两个数的和(或差)的平方,
这两个数乘积的 2 倍.
等于
这两个数的平方和
加
(或减)
