期中素能测评 同步练(含答案) 2025-2026学年数学苏科版八年级上册
文档属性
| 名称 | 期中素能测评 同步练(含答案) 2025-2026学年数学苏科版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 378.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览

文档简介
期中素能测评满分:130分
时间:120分钟
一、 选择题(每小题3分,共24分)
1. 下列长度的三根小木棒能摆成三角形的是 ( )
A. 3cm,4cm,8cm B. 6cm,7cm,13cm
C. 5cm,5cm,11cm D. 14cm,13cm,20cm
2. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是 ( )
A. SSS B. SAS
C. AAS D. HL
3. 在△ABC和△A'B'C'中,∠B=∠B'=30°,AB=A'B'=6,AC=A'C'=4.若∠C=n°,则∠C'的度数为( )
A. 30° B. n°
C. n°或180°-n° D. 30°或150°
4. 若的值与|2b+1|的值互为相反数,则a+2b的算术平方根为 ( )
A. ±2 B. 2
C. ± D.
5. 如图,∠ACB=90°,E,F为AB上的点,AE=AC,BC=BF,则∠ECF的度数为 ( )
A. 44° B. 45°
C. 46° D. 无法确定
6. 如图,△ABC是等边三角形,P为BC上一点,在AC上取一点D,使AD=AP,且∠APD=70°,则∠PAB的度数是 ( )
A. 10° B. 15° C. 20° D. 25°
7. 满足m>|-1|的整数m的值可能是 ( )
A. 3 B. 2 C. 1 D. 0
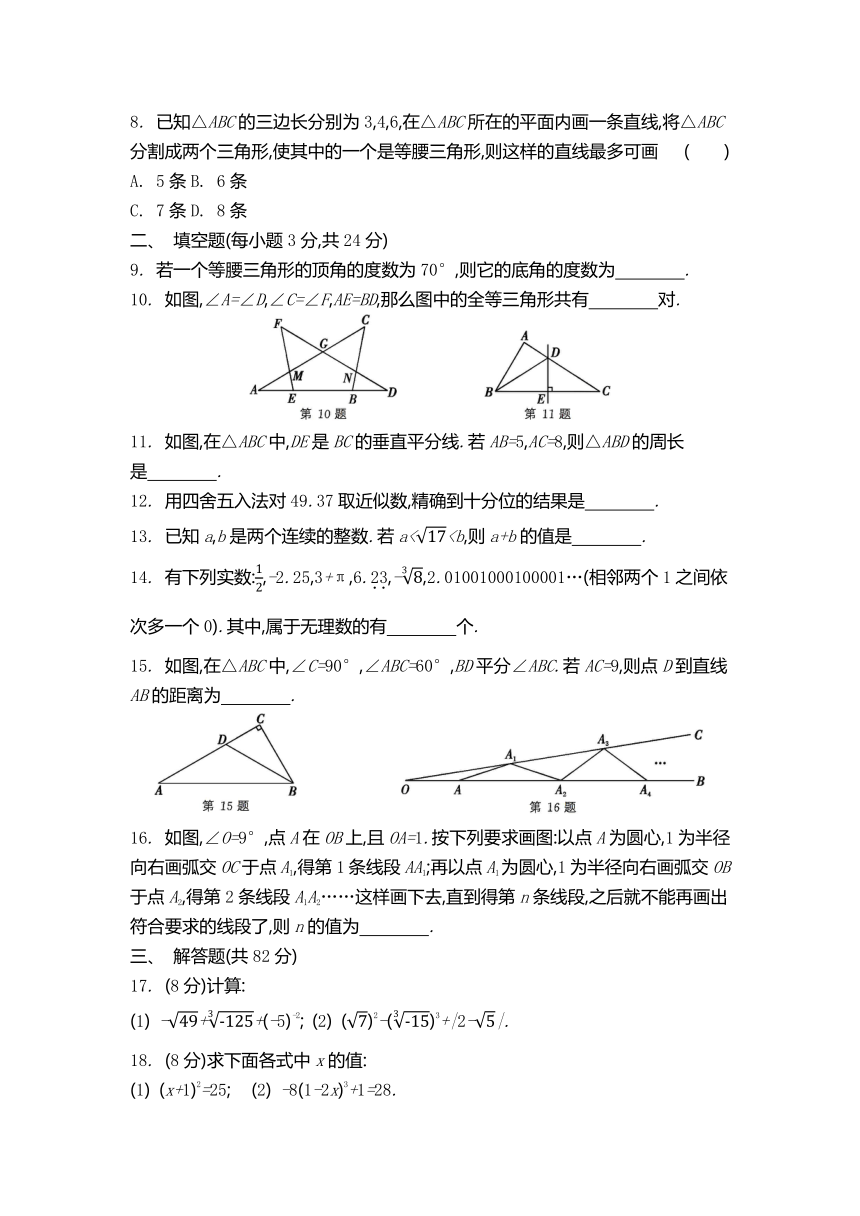
8. 已知△ABC的三边长分别为3,4,6,在△ABC所在的平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 ( )
A. 5条 B. 6条
C. 7条 D. 8条
二、 填空题(每小题3分,共24分)
9. 若一个等腰三角形的顶角的度数为70°,则它的底角的度数为 .
10. 如图,∠A=∠D,∠C=∠F,AE=BD,那么图中的全等三角形共有 对.
11. 如图,在△ABC中,DE是BC的垂直平分线.若AB=5,AC=8,则△ABD的周长是 .
12. 用四舍五入法对49.37取近似数,精确到十分位的结果是 .
13. 已知a,b是两个连续的整数.若a<14. 有下列实数:,-2.25,3+π,6.23,-,2.01001000100001…(相邻两个1之间依次多一个0).其中,属于无理数的有 个.
15. 如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC.若AC=9,则点D到直线AB的距离为 .
16. 如图,∠O=9°,点A在OB上,且OA=1.按下列要求画图:以点A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以点A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2……这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值为 .
三、 解答题(共82分)
17. (8分)计算:
(1) -++(-5)-2; (2) ()2-()3+|2-|.
18. (8分)求下面各式中x的值:
(1) (x+1)2=25; (2) -8(1-2x)3+1=28.
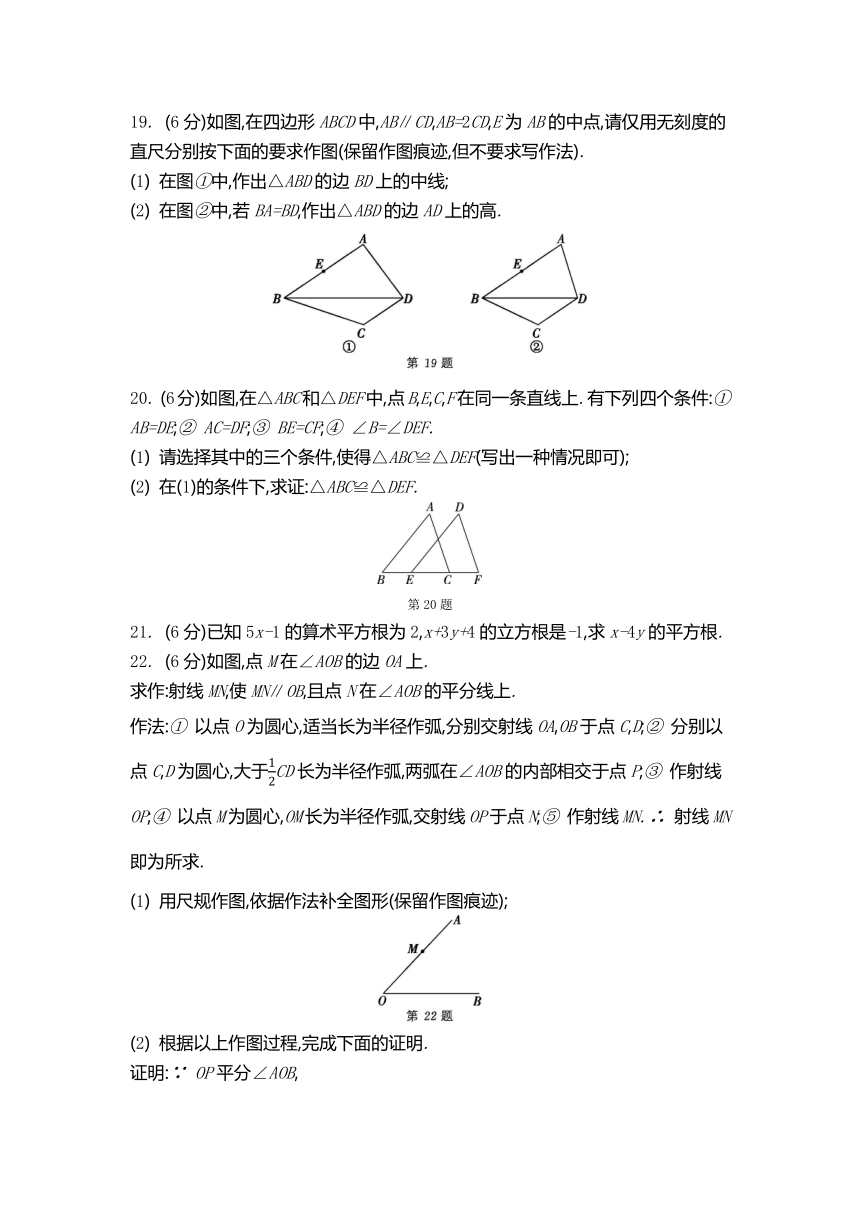
19. (6分)如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度的直尺分别按下面的要求作图(保留作图痕迹,但不要求写作法).
(1) 在图①中,作出△ABD的边BD上的中线;
(2) 在图②中,若BA=BD,作出△ABD的边AD上的高.
20. (6分)如图,在△ABC和△DEF中,点B,E,C,F在同一条直线上.有下列四个条件:① AB=DE;② AC=DF;③ BE=CF;④ ∠B=∠DEF.
(1) 请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可);
(2) 在(1)的条件下,求证:△ABC≌△DEF.
第20题
21. (6分)已知5x-1的算术平方根为2,x+3y+4的立方根是-1,求x-4y的平方根.
22. (6分)如图,点M在∠AOB的边OA上.
求作:射线MN,使MN∥OB,且点N在∠AOB的平分线上.
作法:① 以点O为圆心,适当长为半径作弧,分别交射线OA,OB于点C,D;② 分别以点C,D为圆心,大于CD长为半径作弧,两弧在∠AOB的内部相交于点P;③ 作射线OP;④ 以点M为圆心,OM长为半径作弧,交射线OP于点N;⑤ 作射线MN.∴ 射线MN即为所求.
(1) 用尺规作图,依据作法补全图形(保留作图痕迹);
(2) 根据以上作图过程,完成下面的证明.
证明:∵ OP平分∠AOB,
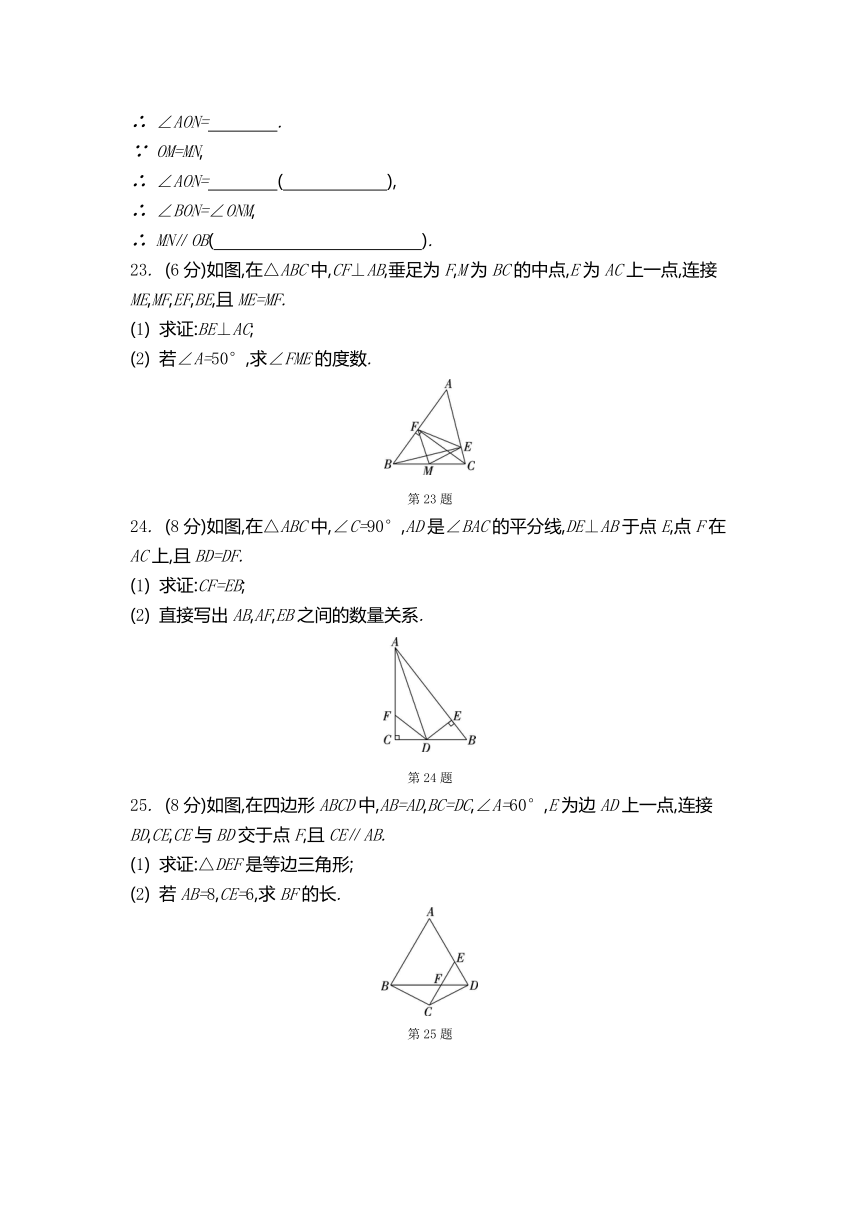
∴ ∠AON= .
∵ OM=MN,
∴ ∠AON= ( ),
∴ ∠BON=∠ONM,
∴ MN∥OB( ).
23. (6分)如图,在△ABC中,CF⊥AB,垂足为F,M为BC的中点,E为AC上一点,连接ME,MF,EF,BE,且ME=MF.
(1) 求证:BE⊥AC;
(2) 若∠A=50°,求∠FME的度数.
第23题
24. (8分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,且BD=DF.
(1) 求证:CF=EB;
(2) 直接写出AB,AF,EB之间的数量关系.
第24题
25. (8分)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,E为边AD上一点,连接BD,CE,CE与BD交于点F,且CE∥AB.
(1) 求证:△DEF是等边三角形;
(2) 若AB=8,CE=6,求BF的长.
第25题
26. (10分)如图①,把两个边长为1的小正方形沿对角线剪开,将所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.
(1) 图②中A,B两点表示的数分别为 , .
(2) 请你参照上面的方法:
① 把图③中5×1的长方形进行裁剪,并拼成一个大正方形.在图③中画出裁剪线,并在图④的正方形网格中画出拼成的大正方形,该大正方形的边长a= (注:小正方形的边长都为1,拼接不重叠也无空隙).
② 在①的基础上,参照图②的画法,请在图⑤的数轴上分别用点M,N表示数a以及a-3.
27. (10分)如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D,E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,同时,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D,E分别作DM⊥PQ,EN⊥PQ,垂足分别为M,N,若AC=6cm,BC=8cm,设运动时间为ts.
(1) 分别求出在此运动过程中,点D与点E的运动时长;
(2) 当以D,M,C为顶点的三角形与以E,N,C为顶点的三角形全等时,求满足条件的t的值.
第27题
期中素能测评
一、 1. D 2. B 3. C 4. D 5. B 6. C 7. A
8. C 解析:如图,先用直尺与圆规画出三边长分别为3,4,6的△ABC,再利用直尺与圆规画出满足题意的点D1~D7,构成7个等腰三角形,即满足题意的直线最多可画7条.具体如下:以AC为底时,AD1=CD1;以AC为腰时,AC=AD2,CA=CD3,CA=CD4;以AB为底时,AD5=BD5;以BC为底时,CD6=BD6;以BC为腰时,BC=BD7.
二、 9. 55° 10. 3 11. 13 12. 49.4 13. 9 14. 2
15. 3 16. 9
三、 17. (1) 原式=-7+(-5)+=-12+=-11 (2) 原式=7-(-15)+(-2+)=20+
18. (1) 根据平方根的定义,得x+1=±,x+1=±5,即x+1=5或x+1=-5,∴ x=4或-6 (2) 原等式可化为(1-2x)3=-,根据立方根的定义,得1-2x=,1-2x=-,∴ x=
19. (1) 如图①,AF即为所求 解析:证△BEF≌△DCF,得BF=DF.
(2) 如图②,BH即为所求 解析:连接CE,交BD于点F,连接AF,DE,得△ABD的中线的交点G,过点G作△ABD的中线BH.结合“三线合一”,知BH即为△ABD的边AD上的高.
20. (1) ①②③(答案不唯一) (2) ∵ BE=CF,∴ BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中,∴ △ABC≌△DEF(SSS)
21. ∵ 5x-1的算术平方根为2,x+3y+4的立方根是-1,∴ 解得∴ x-4y的平方根为±=±=±=±3
22. (1) 如图所示 (2) ∠BON ∠ONM 等边对等角
内错角相等,两直线平行
23. (1) ∵ CF⊥AB,M为BC的中点,∴ MF=BM=CM=BC.∵ ME=MF,∴ ME=BM=CM,∴ ∠MBE=∠MEB,∠MEC=∠MCE.∵ △BCE的内角和为180°,∴ ∠MEB+∠MEC=×180°=90°,∴ ∠BEC=90°,∴ BE⊥AC (2) ∵ ∠A=50°,∴ ∠ABC+∠ACB=180°-50°=130°.由(1),得MF=BM,ME=CM,∴ ∠MBF=∠MFB,∠MEC=∠MCE,∴ ∠BMF+∠CME=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(∠ABC+∠ACB)=360°-2×130°=100°,∴ ∠FME=180°-(∠BMF+∠CME)=80°
24. (1) ∵ ∠C=90°,∴ DC⊥AC.∵ AD是∠BAC的平分线,DE⊥AB,∴ DC=DE,∠C=∠DEB=90°.在Rt△DCF和Rt△DEB中,∴ Rt△DCF≌Rt△DEB(HL),∴ CF=EB (2) AB=AF+2EB
25. (1) ∵ AB=AD,∠A=60°,∴ △ABD为等边三角形,∴ AB=BD=AD,∠ABD=∠ADB=60°.∵ CE∥AB,∴ ∠EFD=∠ABD=60°,∴ ∠EFD=∠ADB=60°,∴ EF=ED,∴ △DEF是等边三角形 (2) 如图,连接AC交BD于点G.∵ AB=AD,BC=DC,∴ AC垂直平分BD,∴ ∠BAG=∠DAG=∠BAD=30°.∵ CE∥AB,∴ ∠ACE=∠BAG=30°,∴ ∠DAG=∠ACE,∴ AE=CE=6,∴ ED=AD-AE=AB-AE=8-6=2.∵ △EFD是等边三角形,∴ FD=ED=2,∴ BF=BD-FD=8-2=6
26. (1) - (2) ① 如图①所示 ② 如图②所示
27. (1) 点D的运动时长为(6+8)÷1=14(s),点E的运动时长为(6+8)÷3=(s) (2) ∵ EN⊥PQ,∴ ∠CEN+∠ECN=90°.∵ ∠ACB=∠DCM+∠ECN=90°,∴ ∠DCM=∠CEN.∵ DM⊥PQ,∴ ∠CMD=∠ENC=90°,∴ 当CD=CE时,以D,M,C为顶点的三角形与以E,N,C为顶点的三角形全等.① 当0≤t<时,点D在AC上,点E在BC上,此时CD=(6-t)cm,EC=(8-3t)cm.根据题意,得6-t=8-3t,解得t=1;② 当
时间:120分钟
一、 选择题(每小题3分,共24分)
1. 下列长度的三根小木棒能摆成三角形的是 ( )
A. 3cm,4cm,8cm B. 6cm,7cm,13cm
C. 5cm,5cm,11cm D. 14cm,13cm,20cm
2. 如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是 ( )
A. SSS B. SAS
C. AAS D. HL
3. 在△ABC和△A'B'C'中,∠B=∠B'=30°,AB=A'B'=6,AC=A'C'=4.若∠C=n°,则∠C'的度数为( )
A. 30° B. n°
C. n°或180°-n° D. 30°或150°
4. 若的值与|2b+1|的值互为相反数,则a+2b的算术平方根为 ( )
A. ±2 B. 2
C. ± D.
5. 如图,∠ACB=90°,E,F为AB上的点,AE=AC,BC=BF,则∠ECF的度数为 ( )
A. 44° B. 45°
C. 46° D. 无法确定
6. 如图,△ABC是等边三角形,P为BC上一点,在AC上取一点D,使AD=AP,且∠APD=70°,则∠PAB的度数是 ( )
A. 10° B. 15° C. 20° D. 25°
7. 满足m>|-1|的整数m的值可能是 ( )
A. 3 B. 2 C. 1 D. 0
8. 已知△ABC的三边长分别为3,4,6,在△ABC所在的平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 ( )
A. 5条 B. 6条
C. 7条 D. 8条
二、 填空题(每小题3分,共24分)
9. 若一个等腰三角形的顶角的度数为70°,则它的底角的度数为 .
10. 如图,∠A=∠D,∠C=∠F,AE=BD,那么图中的全等三角形共有 对.
11. 如图,在△ABC中,DE是BC的垂直平分线.若AB=5,AC=8,则△ABD的周长是 .
12. 用四舍五入法对49.37取近似数,精确到十分位的结果是 .
13. 已知a,b是两个连续的整数.若a<
15. 如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC.若AC=9,则点D到直线AB的距离为 .
16. 如图,∠O=9°,点A在OB上,且OA=1.按下列要求画图:以点A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以点A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2……这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值为 .
三、 解答题(共82分)
17. (8分)计算:
(1) -++(-5)-2; (2) ()2-()3+|2-|.
18. (8分)求下面各式中x的值:
(1) (x+1)2=25; (2) -8(1-2x)3+1=28.
19. (6分)如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度的直尺分别按下面的要求作图(保留作图痕迹,但不要求写作法).
(1) 在图①中,作出△ABD的边BD上的中线;
(2) 在图②中,若BA=BD,作出△ABD的边AD上的高.
20. (6分)如图,在△ABC和△DEF中,点B,E,C,F在同一条直线上.有下列四个条件:① AB=DE;② AC=DF;③ BE=CF;④ ∠B=∠DEF.
(1) 请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可);
(2) 在(1)的条件下,求证:△ABC≌△DEF.
第20题
21. (6分)已知5x-1的算术平方根为2,x+3y+4的立方根是-1,求x-4y的平方根.
22. (6分)如图,点M在∠AOB的边OA上.
求作:射线MN,使MN∥OB,且点N在∠AOB的平分线上.
作法:① 以点O为圆心,适当长为半径作弧,分别交射线OA,OB于点C,D;② 分别以点C,D为圆心,大于CD长为半径作弧,两弧在∠AOB的内部相交于点P;③ 作射线OP;④ 以点M为圆心,OM长为半径作弧,交射线OP于点N;⑤ 作射线MN.∴ 射线MN即为所求.
(1) 用尺规作图,依据作法补全图形(保留作图痕迹);
(2) 根据以上作图过程,完成下面的证明.
证明:∵ OP平分∠AOB,
∴ ∠AON= .
∵ OM=MN,
∴ ∠AON= ( ),
∴ ∠BON=∠ONM,
∴ MN∥OB( ).
23. (6分)如图,在△ABC中,CF⊥AB,垂足为F,M为BC的中点,E为AC上一点,连接ME,MF,EF,BE,且ME=MF.
(1) 求证:BE⊥AC;
(2) 若∠A=50°,求∠FME的度数.
第23题
24. (8分)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,且BD=DF.
(1) 求证:CF=EB;
(2) 直接写出AB,AF,EB之间的数量关系.
第24题
25. (8分)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,E为边AD上一点,连接BD,CE,CE与BD交于点F,且CE∥AB.
(1) 求证:△DEF是等边三角形;
(2) 若AB=8,CE=6,求BF的长.
第25题
26. (10分)如图①,把两个边长为1的小正方形沿对角线剪开,将所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.
(1) 图②中A,B两点表示的数分别为 , .
(2) 请你参照上面的方法:
① 把图③中5×1的长方形进行裁剪,并拼成一个大正方形.在图③中画出裁剪线,并在图④的正方形网格中画出拼成的大正方形,该大正方形的边长a= (注:小正方形的边长都为1,拼接不重叠也无空隙).
② 在①的基础上,参照图②的画法,请在图⑤的数轴上分别用点M,N表示数a以及a-3.
27. (10分)如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D,E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,同时,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D,E分别作DM⊥PQ,EN⊥PQ,垂足分别为M,N,若AC=6cm,BC=8cm,设运动时间为ts.
(1) 分别求出在此运动过程中,点D与点E的运动时长;
(2) 当以D,M,C为顶点的三角形与以E,N,C为顶点的三角形全等时,求满足条件的t的值.
第27题
期中素能测评
一、 1. D 2. B 3. C 4. D 5. B 6. C 7. A
8. C 解析:如图,先用直尺与圆规画出三边长分别为3,4,6的△ABC,再利用直尺与圆规画出满足题意的点D1~D7,构成7个等腰三角形,即满足题意的直线最多可画7条.具体如下:以AC为底时,AD1=CD1;以AC为腰时,AC=AD2,CA=CD3,CA=CD4;以AB为底时,AD5=BD5;以BC为底时,CD6=BD6;以BC为腰时,BC=BD7.
二、 9. 55° 10. 3 11. 13 12. 49.4 13. 9 14. 2
15. 3 16. 9
三、 17. (1) 原式=-7+(-5)+=-12+=-11 (2) 原式=7-(-15)+(-2+)=20+
18. (1) 根据平方根的定义,得x+1=±,x+1=±5,即x+1=5或x+1=-5,∴ x=4或-6 (2) 原等式可化为(1-2x)3=-,根据立方根的定义,得1-2x=,1-2x=-,∴ x=
19. (1) 如图①,AF即为所求 解析:证△BEF≌△DCF,得BF=DF.
(2) 如图②,BH即为所求 解析:连接CE,交BD于点F,连接AF,DE,得△ABD的中线的交点G,过点G作△ABD的中线BH.结合“三线合一”,知BH即为△ABD的边AD上的高.
20. (1) ①②③(答案不唯一) (2) ∵ BE=CF,∴ BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中,∴ △ABC≌△DEF(SSS)
21. ∵ 5x-1的算术平方根为2,x+3y+4的立方根是-1,∴ 解得∴ x-4y的平方根为±=±=±=±3
22. (1) 如图所示 (2) ∠BON ∠ONM 等边对等角
内错角相等,两直线平行
23. (1) ∵ CF⊥AB,M为BC的中点,∴ MF=BM=CM=BC.∵ ME=MF,∴ ME=BM=CM,∴ ∠MBE=∠MEB,∠MEC=∠MCE.∵ △BCE的内角和为180°,∴ ∠MEB+∠MEC=×180°=90°,∴ ∠BEC=90°,∴ BE⊥AC (2) ∵ ∠A=50°,∴ ∠ABC+∠ACB=180°-50°=130°.由(1),得MF=BM,ME=CM,∴ ∠MBF=∠MFB,∠MEC=∠MCE,∴ ∠BMF+∠CME=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(∠ABC+∠ACB)=360°-2×130°=100°,∴ ∠FME=180°-(∠BMF+∠CME)=80°
24. (1) ∵ ∠C=90°,∴ DC⊥AC.∵ AD是∠BAC的平分线,DE⊥AB,∴ DC=DE,∠C=∠DEB=90°.在Rt△DCF和Rt△DEB中,∴ Rt△DCF≌Rt△DEB(HL),∴ CF=EB (2) AB=AF+2EB
25. (1) ∵ AB=AD,∠A=60°,∴ △ABD为等边三角形,∴ AB=BD=AD,∠ABD=∠ADB=60°.∵ CE∥AB,∴ ∠EFD=∠ABD=60°,∴ ∠EFD=∠ADB=60°,∴ EF=ED,∴ △DEF是等边三角形 (2) 如图,连接AC交BD于点G.∵ AB=AD,BC=DC,∴ AC垂直平分BD,∴ ∠BAG=∠DAG=∠BAD=30°.∵ CE∥AB,∴ ∠ACE=∠BAG=30°,∴ ∠DAG=∠ACE,∴ AE=CE=6,∴ ED=AD-AE=AB-AE=8-6=2.∵ △EFD是等边三角形,∴ FD=ED=2,∴ BF=BD-FD=8-2=6
26. (1) - (2) ① 如图①所示 ② 如图②所示
27. (1) 点D的运动时长为(6+8)÷1=14(s),点E的运动时长为(6+8)÷3=(s) (2) ∵ EN⊥PQ,∴ ∠CEN+∠ECN=90°.∵ ∠ACB=∠DCM+∠ECN=90°,∴ ∠DCM=∠CEN.∵ DM⊥PQ,∴ ∠CMD=∠ENC=90°,∴ 当CD=CE时,以D,M,C为顶点的三角形与以E,N,C为顶点的三角形全等.① 当0≤t<时,点D在AC上,点E在BC上,此时CD=(6-t)cm,EC=(8-3t)cm.根据题意,得6-t=8-3t,解得t=1;② 当
同课章节目录
