第4章 平面直角坐标系 整合提升 同步练 (含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 第4章 平面直角坐标系 整合提升 同步练 (含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 198.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 21:56:52 | ||
图片预览


文档简介
第4章 平面直角坐标系
整合提升
考点一 平面直角坐标系
1. (2024·广元)如果单项式-x2my3与单项式2x4y2-n的和仍是一个单项式,那么在平面直角坐标系中点(m,n)在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. (新情境·现实生活)如图,这是一个利用平面直角坐标系画出的某学校的示意图.若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,且综合楼和食堂的坐标分别是(4,1)和(5,4),则教学楼的坐标是 ( )
A. (1,1) B. (1,2) C. (2,1) D. (2,2)
3. 点Q(-3,-1)到x轴的距离为 ,到原点O的距离为 .
4. (2023·日照)若点M(m+3,m-1)在第四象限,则m的取值范围是 .
5. 如图,在长方形ABCD中,点A,B,C的坐标分别为(-3,2),(3,2),(3,-1),则点D的坐标为 .
6. (2024·临夏)如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(4,1),点C的坐标为(3,4),点D在第一象限(不与点C重合),且△ABD与△ABC全等,点D的坐标是 .
7. 勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标(如图,单位:km).笔直铁路经过A,B两地.
(1) A,B两地间的距离为 km;
(2) 计划修一条从C地到铁路AB的最短公路l,并在l上建一个维修站D,使维修站D到A,C两地的距离相等,求C,D两地间的距离.
第7题
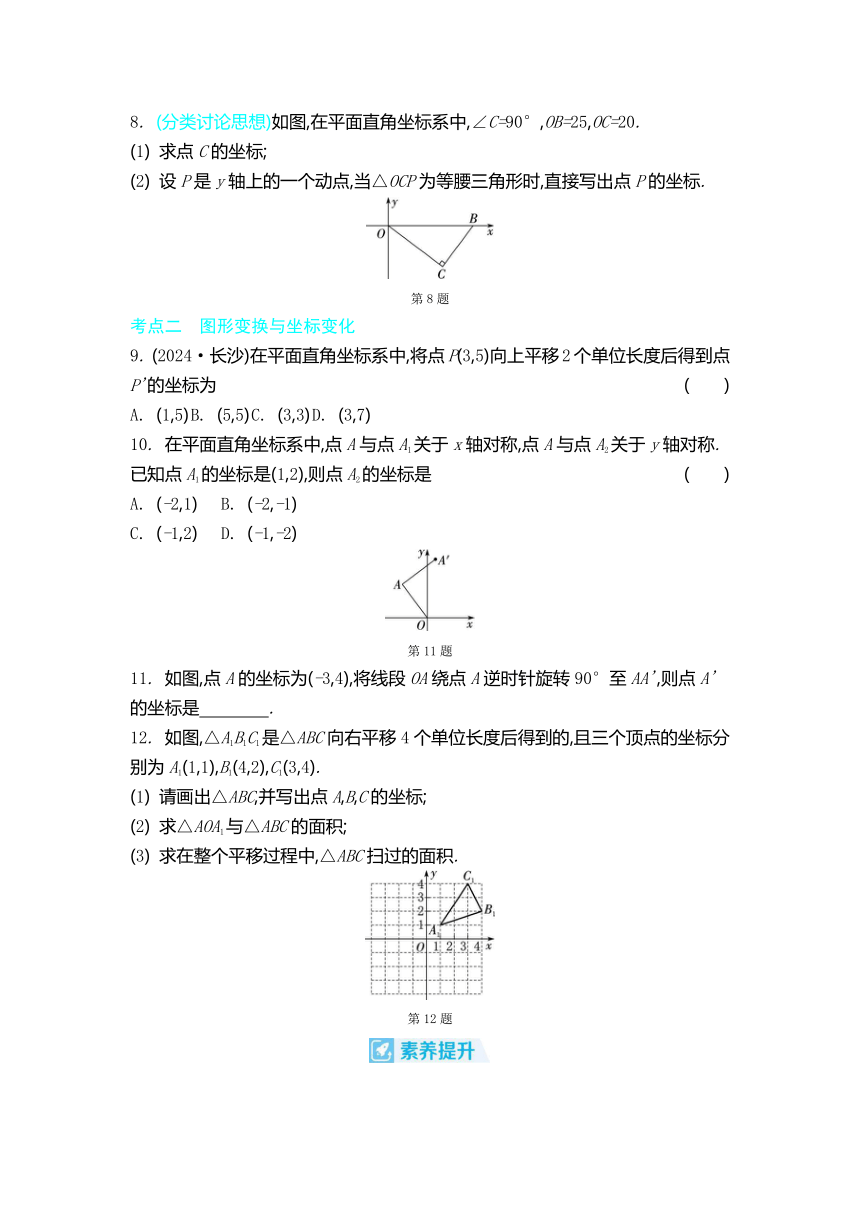
8. (分类讨论思想)如图,在平面直角坐标系中,∠C=90°,OB=25,OC=20.
(1) 求点C的坐标;
(2) 设P是y轴上的一个动点,当△OCP为等腰三角形时,直接写出点P的坐标.
第8题
考点二 图形变换与坐标变化
9. (2024·长沙)在平面直角坐标系中,将点P(3,5)向上平移2个单位长度后得到点P'的坐标为 ( )
A. (1,5) B. (5,5) C. (3,3) D. (3,7)
10. 在平面直角坐标系中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1的坐标是(1,2),则点A2的坐标是 ( )
A. (-2,1) B. (-2,-1)
C. (-1,2) D. (-1,-2)
第11题
11. 如图,点A的坐标为(-3,4),将线段OA绕点A逆时针旋转90°至AA',则点A'的坐标是 .
12. 如图,△A1B1C1是△ABC向右平移4个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1) 请画出△ABC,并写出点A,B,C的坐标;
(2) 求△AOA1与△ABC的面积;
(3) 求在整个平移过程中,△ABC扫过的面积.
第12题
13. 在平面直角坐标系中,已知点A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是 ( )
A. 5 B. 6 C. 7 D. 8
第14题
14. (2023·金华)如图,两个灯笼的位置A,B的坐标分别是(-3,3),(1,2),将点B先向右平移2个单位长度,再向上平移1个单位长度得到点B',则关于点A,B'的位置描述正确的是 ( )
A. 关于x轴对称 B. 关于y轴对称
C. 关于原点对称 D. 关于点B对称
15. (新考法·阅读理解)在平面直角坐标系中,对于平面内任意一点(a,b),规定下列三种变换:① △(a,b)=(-a,b);② ○(a,b)=(-a,-b);③ Ω(a,b)=(a,-b).例如:△[○(1,2)]=(1,-2),则○[Ω(3,4)]= .
16. (新考法·新定义题)(2024·威海改编)在平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b) (c,d)=(a+c,b+d),则称Q(a+c,b+d)为点M,N的“和点”.若以原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”.现有点A(2,5),B(-1,3),如果以O,A,B,C四点为顶点的四边形是“和点四边形”,那么点C的坐标是 .
17. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1) 作出△ABC关于原点O对称的△A1B1C1;
(2) 作出点A关于x轴的对称点A',若把点A'向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界),则a的取值范围是 .
18. 如图,在平面直角坐标系中,点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1第18题
第4章 平面直角坐标系 整合提升
1. D 2. D 3. 1 4. -36. (1,4)
7. (1) 20 (2) 如图,过点C作CE⊥AB于点E,连接AC,作AC的垂直平分线,交CE于点D,连接AD.由图,易知CE=1-(-17)=18(km).设CD=xkm,则ED=(18-x)km.在Rt△EDA中,ED=(18-x)km,AD=CD=xkm,AE=12km,∴ x2=(18-x)2+122,解得x=13,∴ C,D两地间的距离为13km
8. (1) 如图,过点C作CH⊥OB,垂足为H.∵ 在Rt△OCB中,∠OCB=90°,OB=25,OC=20,∴ BC2+OC2=OB2,即BC2+202=252,∴ BC=15.根据△OCB的面积公式,得OB·CH=OC·BC,∴ CH===12.∵ 在Rt△OHC中,∠OHC=90°,∴ OH2+CH2=OC2,即OH2+122=202,∴ OH=16,∴ 点C的坐标为(16,-12) (2) 当OC为△OCP的腰时,点P的坐标为(0,20)或(0,-20)或(0,-24);当OC为△OCP的底时,点P的坐标为
9. D 10. D
11. (1,7) 解析:过点A作y轴的平行线EF,交x轴于点N,再过点A'作EF的垂线,垂足为M.先证△A'MA≌△ANO(AAS),则A'M=AN,MA=NO.∵ 点A的坐标为(-3,4),∴ A'M=AN=4,MA=NO=3,∴ 4-3=1,4+3=7,∴ 点A'的坐标为(1,7).
12. (1) 如图,△ABC即为所求 A(-3,1),B(0,2),C(-1,4) (2) 如图,连接AO,A1O,AA1.△AOA1的面积为×4×1=2,△ABC的面积为3×3-×2×3-×1×2-×1×3= (3) 如图,连接CC1.由平移的性质,可知S△ABC=,∴ △ABC扫过的面积为+=+S△ABC=4×3+=
13. A 14. B
15. (-3,4) 解析:∵ Ω(a,b)=(a,-b),∴ Ω(3,4)=(3,-4).∵ ○(a,b)=(-a,-b),∴ ○(3,-4)=(-3,4),∴ ○[Ω(3,4)]=(-3,4).
16. (1,8)或(-3,-2)或(3,2)
17. (1) 如图,△A1B1C1即为所求 解析:描出A1(2,2),B1(4,1),C1(4,4)三点,再依次连接即可.
(2) 如图,点A'即为所求 418. 设n-m=t.∵ A(1,m+1),B(a,m+1),1
整合提升
考点一 平面直角坐标系
1. (2024·广元)如果单项式-x2my3与单项式2x4y2-n的和仍是一个单项式,那么在平面直角坐标系中点(m,n)在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. (新情境·现实生活)如图,这是一个利用平面直角坐标系画出的某学校的示意图.若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,且综合楼和食堂的坐标分别是(4,1)和(5,4),则教学楼的坐标是 ( )
A. (1,1) B. (1,2) C. (2,1) D. (2,2)
3. 点Q(-3,-1)到x轴的距离为 ,到原点O的距离为 .
4. (2023·日照)若点M(m+3,m-1)在第四象限,则m的取值范围是 .
5. 如图,在长方形ABCD中,点A,B,C的坐标分别为(-3,2),(3,2),(3,-1),则点D的坐标为 .
6. (2024·临夏)如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(4,1),点C的坐标为(3,4),点D在第一象限(不与点C重合),且△ABD与△ABC全等,点D的坐标是 .
7. 勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标(如图,单位:km).笔直铁路经过A,B两地.
(1) A,B两地间的距离为 km;
(2) 计划修一条从C地到铁路AB的最短公路l,并在l上建一个维修站D,使维修站D到A,C两地的距离相等,求C,D两地间的距离.
第7题
8. (分类讨论思想)如图,在平面直角坐标系中,∠C=90°,OB=25,OC=20.
(1) 求点C的坐标;
(2) 设P是y轴上的一个动点,当△OCP为等腰三角形时,直接写出点P的坐标.
第8题
考点二 图形变换与坐标变化
9. (2024·长沙)在平面直角坐标系中,将点P(3,5)向上平移2个单位长度后得到点P'的坐标为 ( )
A. (1,5) B. (5,5) C. (3,3) D. (3,7)
10. 在平面直角坐标系中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1的坐标是(1,2),则点A2的坐标是 ( )
A. (-2,1) B. (-2,-1)
C. (-1,2) D. (-1,-2)
第11题
11. 如图,点A的坐标为(-3,4),将线段OA绕点A逆时针旋转90°至AA',则点A'的坐标是 .
12. 如图,△A1B1C1是△ABC向右平移4个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1) 请画出△ABC,并写出点A,B,C的坐标;
(2) 求△AOA1与△ABC的面积;
(3) 求在整个平移过程中,△ABC扫过的面积.
第12题
13. 在平面直角坐标系中,已知点A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是 ( )
A. 5 B. 6 C. 7 D. 8
第14题
14. (2023·金华)如图,两个灯笼的位置A,B的坐标分别是(-3,3),(1,2),将点B先向右平移2个单位长度,再向上平移1个单位长度得到点B',则关于点A,B'的位置描述正确的是 ( )
A. 关于x轴对称 B. 关于y轴对称
C. 关于原点对称 D. 关于点B对称
15. (新考法·阅读理解)在平面直角坐标系中,对于平面内任意一点(a,b),规定下列三种变换:① △(a,b)=(-a,b);② ○(a,b)=(-a,-b);③ Ω(a,b)=(a,-b).例如:△[○(1,2)]=(1,-2),则○[Ω(3,4)]= .
16. (新考法·新定义题)(2024·威海改编)在平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b) (c,d)=(a+c,b+d),则称Q(a+c,b+d)为点M,N的“和点”.若以原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”.现有点A(2,5),B(-1,3),如果以O,A,B,C四点为顶点的四边形是“和点四边形”,那么点C的坐标是 .
17. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1) 作出△ABC关于原点O对称的△A1B1C1;
(2) 作出点A关于x轴的对称点A',若把点A'向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界),则a的取值范围是 .
18. 如图,在平面直角坐标系中,点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1
第4章 平面直角坐标系 整合提升
1. D 2. D 3. 1 4. -3
7. (1) 20 (2) 如图,过点C作CE⊥AB于点E,连接AC,作AC的垂直平分线,交CE于点D,连接AD.由图,易知CE=1-(-17)=18(km).设CD=xkm,则ED=(18-x)km.在Rt△EDA中,ED=(18-x)km,AD=CD=xkm,AE=12km,∴ x2=(18-x)2+122,解得x=13,∴ C,D两地间的距离为13km
8. (1) 如图,过点C作CH⊥OB,垂足为H.∵ 在Rt△OCB中,∠OCB=90°,OB=25,OC=20,∴ BC2+OC2=OB2,即BC2+202=252,∴ BC=15.根据△OCB的面积公式,得OB·CH=OC·BC,∴ CH===12.∵ 在Rt△OHC中,∠OHC=90°,∴ OH2+CH2=OC2,即OH2+122=202,∴ OH=16,∴ 点C的坐标为(16,-12) (2) 当OC为△OCP的腰时,点P的坐标为(0,20)或(0,-20)或(0,-24);当OC为△OCP的底时,点P的坐标为
9. D 10. D
11. (1,7) 解析:过点A作y轴的平行线EF,交x轴于点N,再过点A'作EF的垂线,垂足为M.先证△A'MA≌△ANO(AAS),则A'M=AN,MA=NO.∵ 点A的坐标为(-3,4),∴ A'M=AN=4,MA=NO=3,∴ 4-3=1,4+3=7,∴ 点A'的坐标为(1,7).
12. (1) 如图,△ABC即为所求 A(-3,1),B(0,2),C(-1,4) (2) 如图,连接AO,A1O,AA1.△AOA1的面积为×4×1=2,△ABC的面积为3×3-×2×3-×1×2-×1×3= (3) 如图,连接CC1.由平移的性质,可知S△ABC=,∴ △ABC扫过的面积为+=+S△ABC=4×3+=
13. A 14. B
15. (-3,4) 解析:∵ Ω(a,b)=(a,-b),∴ Ω(3,4)=(3,-4).∵ ○(a,b)=(-a,-b),∴ ○(3,-4)=(-3,4),∴ ○[Ω(3,4)]=(-3,4).
16. (1,8)或(-3,-2)或(3,2)
17. (1) 如图,△A1B1C1即为所求 解析:描出A1(2,2),B1(4,1),C1(4,4)三点,再依次连接即可.
(2) 如图,点A'即为所求 4
同课章节目录
