阶段训练(1.2~1.3) 同步练 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 阶段训练(1.2~1.3) 同步练 2025-2026学年数学苏科版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 89.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览

文档简介
阶段训练(1.2~1.3)
一、 选择题
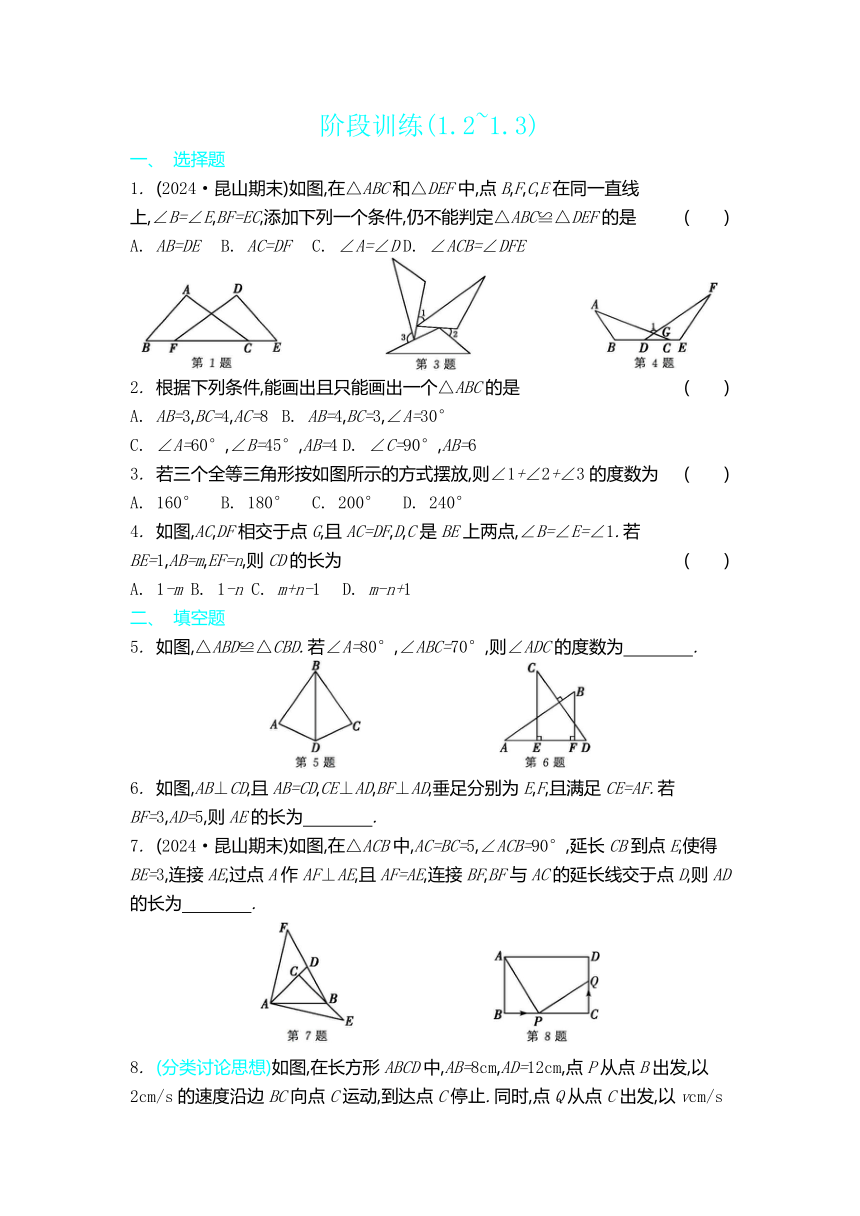
1. (2024·昆山期末)如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,∠B=∠E,BF=EC,添加下列一个条件,仍不能判定△ABC≌△DEF的是 ( )
A. AB=DE B. AC=DF C. ∠A=∠D D. ∠ACB=∠DFE
2. 根据下列条件,能画出且只能画出一个△ABC的是 ( )
A. AB=3,BC=4,AC=8 B. AB=4,BC=3,∠A=30°
C. ∠A=60°,∠B=45°,AB=4 D. ∠C=90°,AB=6
3. 若三个全等三角形按如图所示的方式摆放,则∠1+∠2+∠3的度数为 ( )
A. 160° B. 180° C. 200° D. 240°
4. 如图,AC,DF相交于点G,且AC=DF,D,C是BE上两点,∠B=∠E=∠1.若BE=1,AB=m,EF=n,则CD的长为 ( )
A. 1-m B. 1-n C. m+n-1 D. m-n+1
二、 填空题
5. 如图,△ABD≌△CBD.若∠A=80°,∠ABC=70°,则∠ADC的度数为 .
6. 如图,AB⊥CD,且AB=CD,CE⊥AD,BF⊥AD,垂足分别为E,F,且满足CE=AF.若BF=3,AD=5,则AE的长为 .
7. (2024·昆山期末)如图,在△ACB中,AC=BC=5,∠ACB=90°,延长CB到点E,使得BE=3,连接AE,过点A作AF⊥AE,且AF=AE,连接BF,BF与AC的延长线交于点D,则AD的长为 .
8. (分类讨论思想)如图,在长方形ABCD中,AB=8cm,AD=12cm,点P从点B出发,以2cm/s的速度沿边BC向点C运动,到达点C停止.同时,点Q从点C出发,以vcm/s的速度沿边CD向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v= 时,△ABP与△PCQ全等.
三、 解答题
9. 如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:
(1) AE∥BF;
(2) DE=CF.
第9题
10. (教材P25例7变式)如图,在四边形ABCD中,点E在AC上,AC既平分∠DAB,又平分∠DCB.求证:DE=BE.
第10题
11. 如图,在四边形ABCD中,AB=AC,∠D=90°,BE⊥AC,垂足为F,且交CD于点E,连接EA,EA平分∠DEF.
(1) 求证:AF=AD;
(2) 若BF=7,DE=3,求CE的长.
第11题
阶段训练(1.2~1.3)
一、 1. B 2. C
3. B 解析:如图,由全等三角形的性质,得∠5=∠10,∠6=∠11.∵ ∠4+∠10+∠11=180°,∴ ∠4+∠5+∠6=180°.∵ (∠1+∠4+∠7)+(∠3+∠5+∠8)+ (∠2+∠6+∠9)=3×180°,∠7+∠8+∠9=180°,∴ ∠1+∠2+∠3=180°.
4. C
二、 5. 130° 6. 2
7. 解析:过点F作FG⊥CD,交CD的延长线于点G.证△AFG≌△EAC,得FG=AC,AG=EC.∵ AC=BC=5,BE=3,∴ AG=EC=8,FG=BC,∴ CG=3.证△FDG≌△BDC,得GD=CD=,∴ AD=AC+CD=.
8. 2或
三、 9. (1) ∵ AD=BC,∴ AD+CD=BC+CD,即AC=BD.在△ACE和△BDF中, ∴ △ACE≌△BDF(SSS),∴ ∠A=∠B,∴ AE∥BF (2) 由(1),知∠A=∠B.在△ADE和△BCF中,∴ △ADE≌△BCF(SAS),∴ DE=CF
10. ∵ AC既平分∠DAB,又平分∠DCB,∴ ∠DAC=∠BAC,∠DCA=∠BCA. 在△ACD和△ACB中, ∴ △ACD≌△ACB(ASA),∴ AD=AB. 在△AED和△AEB中, ∴ △AED≌△AEB(SAS),∴ DE=BE
11. (1) ∵ ∠D=90°,BE⊥AC,∴ ∠AFE=∠D=90°.∵ EA平分∠DEF,∴ ∠FEA=∠DEA.在△FAE和△DAE中,∴ △FAE≌△DAE(AAS),∴ AF=AD (2) ∵ ∠D=90°,BE⊥AC,∴ ∠AFB=∠D=90°,∴ △ABF和△ACD均为直角三角形,∴ 在Rt△ABF和Rt△ACD中, ∴ Rt△ABF≌Rt△ACD(HL),∴ BF=CD=7.∵ DE=3,∴ CE=CD-DE=7-3=4
一、 选择题
1. (2024·昆山期末)如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,∠B=∠E,BF=EC,添加下列一个条件,仍不能判定△ABC≌△DEF的是 ( )
A. AB=DE B. AC=DF C. ∠A=∠D D. ∠ACB=∠DFE
2. 根据下列条件,能画出且只能画出一个△ABC的是 ( )
A. AB=3,BC=4,AC=8 B. AB=4,BC=3,∠A=30°
C. ∠A=60°,∠B=45°,AB=4 D. ∠C=90°,AB=6
3. 若三个全等三角形按如图所示的方式摆放,则∠1+∠2+∠3的度数为 ( )
A. 160° B. 180° C. 200° D. 240°
4. 如图,AC,DF相交于点G,且AC=DF,D,C是BE上两点,∠B=∠E=∠1.若BE=1,AB=m,EF=n,则CD的长为 ( )
A. 1-m B. 1-n C. m+n-1 D. m-n+1
二、 填空题
5. 如图,△ABD≌△CBD.若∠A=80°,∠ABC=70°,则∠ADC的度数为 .
6. 如图,AB⊥CD,且AB=CD,CE⊥AD,BF⊥AD,垂足分别为E,F,且满足CE=AF.若BF=3,AD=5,则AE的长为 .
7. (2024·昆山期末)如图,在△ACB中,AC=BC=5,∠ACB=90°,延长CB到点E,使得BE=3,连接AE,过点A作AF⊥AE,且AF=AE,连接BF,BF与AC的延长线交于点D,则AD的长为 .
8. (分类讨论思想)如图,在长方形ABCD中,AB=8cm,AD=12cm,点P从点B出发,以2cm/s的速度沿边BC向点C运动,到达点C停止.同时,点Q从点C出发,以vcm/s的速度沿边CD向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v= 时,△ABP与△PCQ全等.
三、 解答题
9. 如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:
(1) AE∥BF;
(2) DE=CF.
第9题
10. (教材P25例7变式)如图,在四边形ABCD中,点E在AC上,AC既平分∠DAB,又平分∠DCB.求证:DE=BE.
第10题
11. 如图,在四边形ABCD中,AB=AC,∠D=90°,BE⊥AC,垂足为F,且交CD于点E,连接EA,EA平分∠DEF.
(1) 求证:AF=AD;
(2) 若BF=7,DE=3,求CE的长.
第11题
阶段训练(1.2~1.3)
一、 1. B 2. C
3. B 解析:如图,由全等三角形的性质,得∠5=∠10,∠6=∠11.∵ ∠4+∠10+∠11=180°,∴ ∠4+∠5+∠6=180°.∵ (∠1+∠4+∠7)+(∠3+∠5+∠8)+ (∠2+∠6+∠9)=3×180°,∠7+∠8+∠9=180°,∴ ∠1+∠2+∠3=180°.
4. C
二、 5. 130° 6. 2
7. 解析:过点F作FG⊥CD,交CD的延长线于点G.证△AFG≌△EAC,得FG=AC,AG=EC.∵ AC=BC=5,BE=3,∴ AG=EC=8,FG=BC,∴ CG=3.证△FDG≌△BDC,得GD=CD=,∴ AD=AC+CD=.
8. 2或
三、 9. (1) ∵ AD=BC,∴ AD+CD=BC+CD,即AC=BD.在△ACE和△BDF中, ∴ △ACE≌△BDF(SSS),∴ ∠A=∠B,∴ AE∥BF (2) 由(1),知∠A=∠B.在△ADE和△BCF中,∴ △ADE≌△BCF(SAS),∴ DE=CF
10. ∵ AC既平分∠DAB,又平分∠DCB,∴ ∠DAC=∠BAC,∠DCA=∠BCA. 在△ACD和△ACB中, ∴ △ACD≌△ACB(ASA),∴ AD=AB. 在△AED和△AEB中, ∴ △AED≌△AEB(SAS),∴ DE=BE
11. (1) ∵ ∠D=90°,BE⊥AC,∴ ∠AFE=∠D=90°.∵ EA平分∠DEF,∴ ∠FEA=∠DEA.在△FAE和△DAE中,∴ △FAE≌△DAE(AAS),∴ AF=AD (2) ∵ ∠D=90°,BE⊥AC,∴ ∠AFB=∠D=90°,∴ △ABF和△ACD均为直角三角形,∴ 在Rt△ABF和Rt△ACD中, ∴ Rt△ABF≌Rt△ACD(HL),∴ BF=CD=7.∵ DE=3,∴ CE=CD-DE=7-3=4
同课章节目录
