阶段训练(1.4) 同步练 (含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 阶段训练(1.4) 同步练 (含答案) 2025-2026学年数学苏科版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 243.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览

文档简介
阶段训练(1.4)
一、 选择题
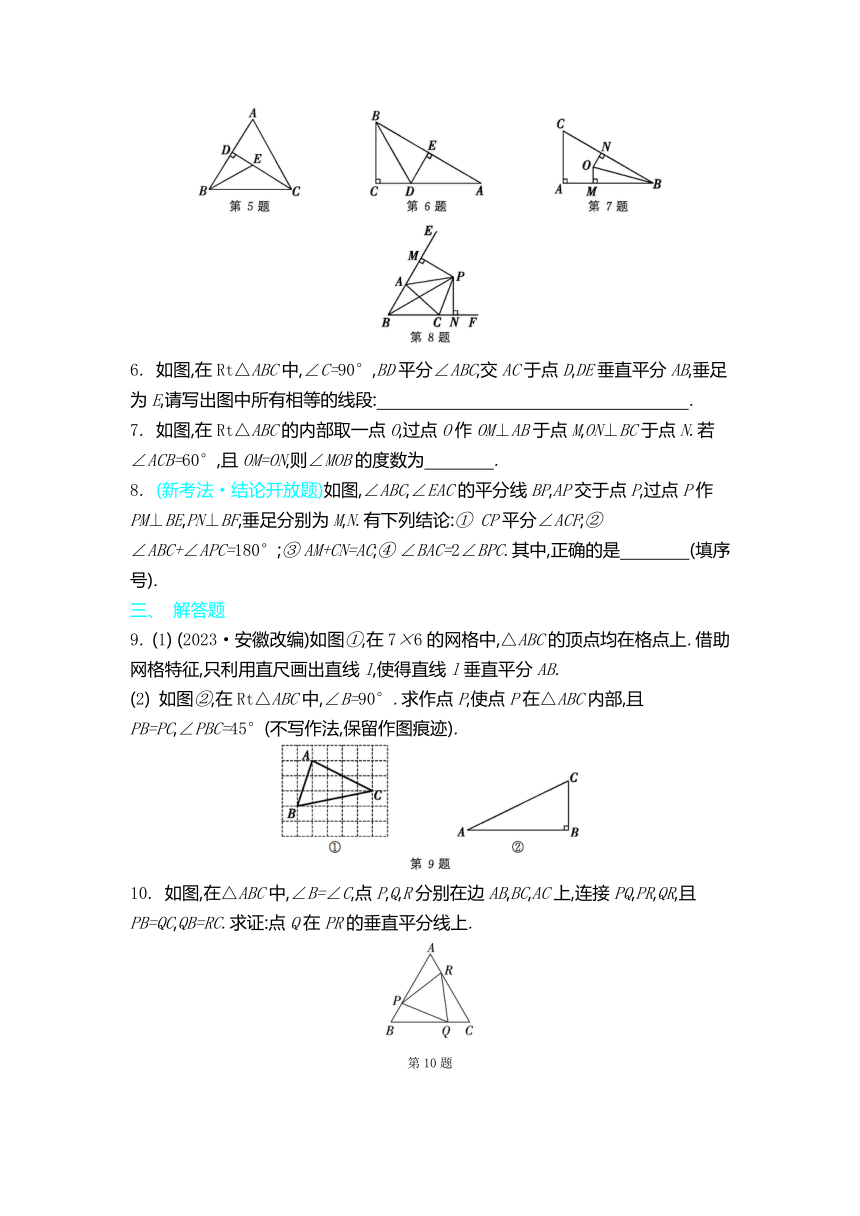
1. (2024·苏州工业园区期中)如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在 ( )
A. AC,BC两边上的高的交点处 B. AC,BC两边上的中线的交点处
C. AC,BC两边的垂直平分线的交点处 D. ∠A,∠B两角的平分线的交点处
2. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF,交AD于点O.有下列三个结论:① OA=OD;② AD⊥EF;③ AE+DF=AF+DE.其中,一定正确的是 ( )
A. ①② B. ①③
C. ②③ D. ①②③
3. 如图,在△ABC中,∠BAC和∠ACB的平分线交于点O,连接OB.若AB=6,BC=9,△ABO的面积为6,则△BCO的面积为 ( )
A. 9 B. 18 C. 13.5 D. 54
4. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB的度数为 ( )
A. 30° B. 35° C. 45° D. 60°
二、 填空题
5. 如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=7,DE=2,则△BCE的面积为 .
6. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,DE垂直平分AB,垂足为E,请写出图中所有相等的线段: .
7. 如图,在Rt△ABC的内部取一点O,过点O作OM⊥AB于点M,ON⊥BC于点N.若∠ACB=60°,且OM=ON,则∠MOB的度数为 .
8. (新考法·结论开放题)如图,∠ABC,∠EAC的平分线BP,AP交于点P,过点P作PM⊥BE,PN⊥BF,垂足分别为M,N.有下列结论:① CP平分∠ACF;② ∠ABC+∠APC=180°;③ AM+CN=AC;④ ∠BAC=2∠BPC.其中,正确的是 (填序号).
三、 解答题
9. (1) (2023·安徽改编)如图①,在7×6的网格中,△ABC的顶点均在格点上.借助网格特征,只利用直尺画出直线l,使得直线l垂直平分AB.
(2) 如图②,在Rt△ABC中,∠B=90°.求作点P,使点P在△ABC内部,且PB=PC,∠PBC=45°(不写作法,保留作图痕迹).
10. 如图,在△ABC中,∠B=∠C,点P,Q,R分别在边AB,BC,AC上,连接PQ,PR,QR,且PB=QC,QB=RC.求证:点Q在PR的垂直平分线上.
第10题
11. 如图,D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF,EF与AB的延长线交于点F,EF∥BC.设点O在AD上,且AO=CO.求证:O是△ABC三边的垂直平分线的交点.
第11题
12. (教材P41习题第9题变式)如图,过△ABC的边AC的垂直平分线MN上的点M,作△ABC的另外两边AB,BC所在直线的垂线,垂足分别为D,E,AD=CE,作射线BM.求证:BM平分∠ABC.
第12题
阶段训练(1.4)
一、 1. C 2. C 3. A
4. B 解析:过点M作MN⊥AD于点N.∵ ∠B=∠C=90°,∴ ∠B+∠C=180°,∴ DC∥AB,∴ ∠ADC+∠DAB=180°.∵ ∠ADC=110°,∴ ∠DAB=70°.∵ DM平分∠ADC,∠C=90°,MN⊥AD,∴ MC=MN.又∵ M是BC的中点,∴ MC=MB,∴ MN=MB.又∵ MN⊥AD,∠B=90°,∴ AM平分∠DAB,∴ ∠MAB=∠DAB=35°.
二、 5. 7 6. BC=BE=EA,CD=ED,BD=AD 7. 75°
8. ①③④
三、 9. (1) 如图①,直线l即为所求 (2) 如图②,点P即为所求
10. 在△BPQ和△CQR中,∴ △BPQ≌△CQR(SAS),∴ QP=RQ,∴ 点Q在PR的垂直平分线上
11. 如图,连接BO.∵ AE⊥EF,∴ ∠E=90°.∵ EF∥BC,∴ ∠ADB=∠E=90°,∴ AD⊥BC.∵ D是BC的中点,∴ AD是BC的垂直平分线,即点O在BC的垂直平分线上,∴ BO=CO.∵ AO=CO,∴ 点O在AC的垂直平分线上,BO=AO,∴ 点O在AB的垂直平分线上,∴ O是△ABC三边的垂直平分线的交点
12. 连接MA,MC.∵ 点M在AC的垂直平分线上,∴ MA=MC.∵ MD⊥AD,ME⊥BC,∴ ∠ADM=∠CEM=90°.在Rt△MAD和Rt△MCE中,∴ Rt△MAD≌Rt△MCE(HL),∴ MD=ME.又∵ MD⊥BA,ME⊥BC,∴ 点M在∠ABC的平分线上,即BM平分∠ABC
一、 选择题
1. (2024·苏州工业园区期中)如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在 ( )
A. AC,BC两边上的高的交点处 B. AC,BC两边上的中线的交点处
C. AC,BC两边的垂直平分线的交点处 D. ∠A,∠B两角的平分线的交点处
2. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF,交AD于点O.有下列三个结论:① OA=OD;② AD⊥EF;③ AE+DF=AF+DE.其中,一定正确的是 ( )
A. ①② B. ①③
C. ②③ D. ①②③
3. 如图,在△ABC中,∠BAC和∠ACB的平分线交于点O,连接OB.若AB=6,BC=9,△ABO的面积为6,则△BCO的面积为 ( )
A. 9 B. 18 C. 13.5 D. 54
4. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB的度数为 ( )
A. 30° B. 35° C. 45° D. 60°
二、 填空题
5. 如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=7,DE=2,则△BCE的面积为 .
6. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,DE垂直平分AB,垂足为E,请写出图中所有相等的线段: .
7. 如图,在Rt△ABC的内部取一点O,过点O作OM⊥AB于点M,ON⊥BC于点N.若∠ACB=60°,且OM=ON,则∠MOB的度数为 .
8. (新考法·结论开放题)如图,∠ABC,∠EAC的平分线BP,AP交于点P,过点P作PM⊥BE,PN⊥BF,垂足分别为M,N.有下列结论:① CP平分∠ACF;② ∠ABC+∠APC=180°;③ AM+CN=AC;④ ∠BAC=2∠BPC.其中,正确的是 (填序号).
三、 解答题
9. (1) (2023·安徽改编)如图①,在7×6的网格中,△ABC的顶点均在格点上.借助网格特征,只利用直尺画出直线l,使得直线l垂直平分AB.
(2) 如图②,在Rt△ABC中,∠B=90°.求作点P,使点P在△ABC内部,且PB=PC,∠PBC=45°(不写作法,保留作图痕迹).
10. 如图,在△ABC中,∠B=∠C,点P,Q,R分别在边AB,BC,AC上,连接PQ,PR,QR,且PB=QC,QB=RC.求证:点Q在PR的垂直平分线上.
第10题
11. 如图,D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF,EF与AB的延长线交于点F,EF∥BC.设点O在AD上,且AO=CO.求证:O是△ABC三边的垂直平分线的交点.
第11题
12. (教材P41习题第9题变式)如图,过△ABC的边AC的垂直平分线MN上的点M,作△ABC的另外两边AB,BC所在直线的垂线,垂足分别为D,E,AD=CE,作射线BM.求证:BM平分∠ABC.
第12题
阶段训练(1.4)
一、 1. C 2. C 3. A
4. B 解析:过点M作MN⊥AD于点N.∵ ∠B=∠C=90°,∴ ∠B+∠C=180°,∴ DC∥AB,∴ ∠ADC+∠DAB=180°.∵ ∠ADC=110°,∴ ∠DAB=70°.∵ DM平分∠ADC,∠C=90°,MN⊥AD,∴ MC=MN.又∵ M是BC的中点,∴ MC=MB,∴ MN=MB.又∵ MN⊥AD,∠B=90°,∴ AM平分∠DAB,∴ ∠MAB=∠DAB=35°.
二、 5. 7 6. BC=BE=EA,CD=ED,BD=AD 7. 75°
8. ①③④
三、 9. (1) 如图①,直线l即为所求 (2) 如图②,点P即为所求
10. 在△BPQ和△CQR中,∴ △BPQ≌△CQR(SAS),∴ QP=RQ,∴ 点Q在PR的垂直平分线上
11. 如图,连接BO.∵ AE⊥EF,∴ ∠E=90°.∵ EF∥BC,∴ ∠ADB=∠E=90°,∴ AD⊥BC.∵ D是BC的中点,∴ AD是BC的垂直平分线,即点O在BC的垂直平分线上,∴ BO=CO.∵ AO=CO,∴ 点O在AC的垂直平分线上,BO=AO,∴ 点O在AB的垂直平分线上,∴ O是△ABC三边的垂直平分线的交点
12. 连接MA,MC.∵ 点M在AC的垂直平分线上,∴ MA=MC.∵ MD⊥AD,ME⊥BC,∴ ∠ADM=∠CEM=90°.在Rt△MAD和Rt△MCE中,∴ Rt△MAD≌Rt△MCE(HL),∴ MD=ME.又∵ MD⊥BA,ME⊥BC,∴ 点M在∠ABC的平分线上,即BM平分∠ABC
同课章节目录
