期末复习专题 专题(一) 三 角 形 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 期末复习专题 专题(一) 三 角 形 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 139.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 22:09:22 | ||
图片预览


文档简介
期末复习专题
专题(一) 三 角 形
1. 在△ABC中,若AB=2,AC=4,且BC的长为整数,则△ABC的周长可能是 ( )
A. 8 B. 11 C. 12 D. 15
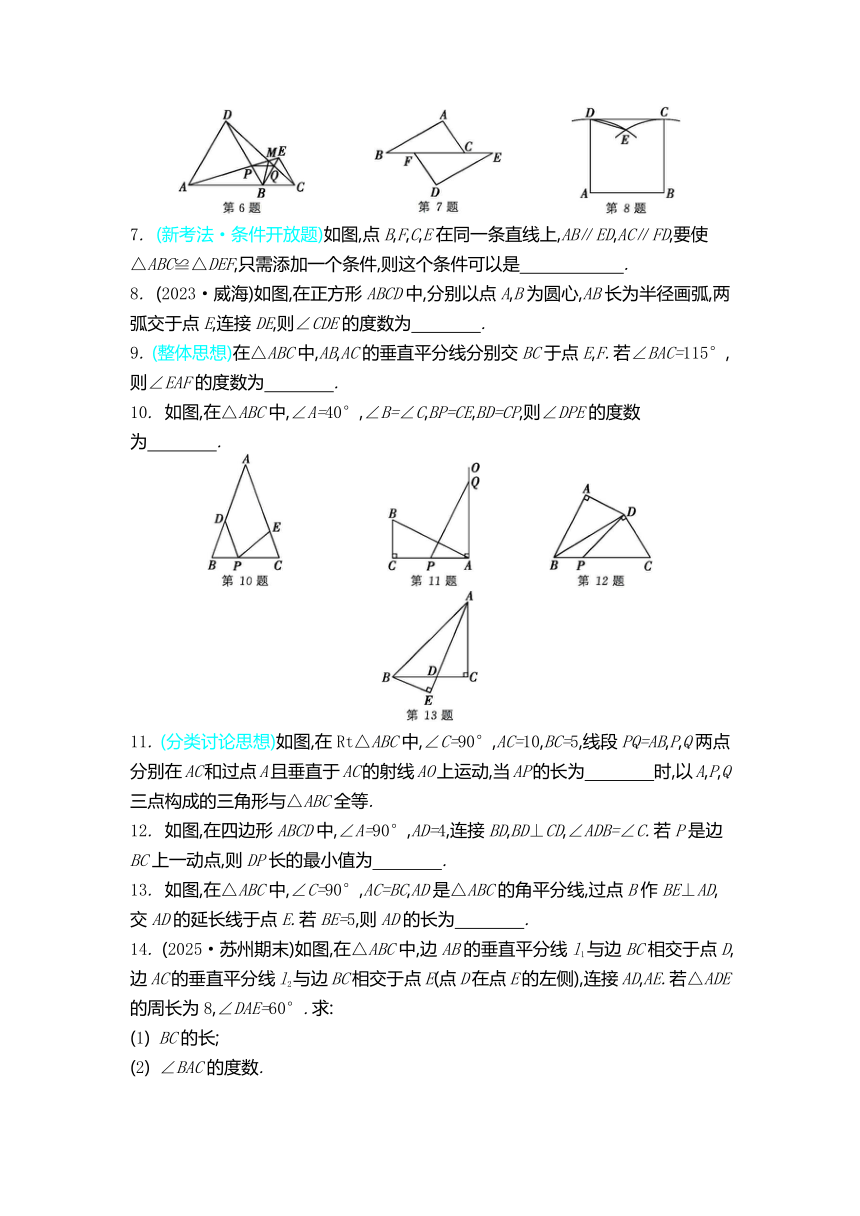
2. 如图,点D,E分别在△ABC的边上,连接AD,CE,DE,且AD,CE交于点F.若∠ACE=∠ACB,BC=2BD,则下列说法错误的是 ( )
A. AD是△ABC的中线 B. S△BDE=S△CDE
C. CE是△ADC的角平分线 D. ∠ACB=2∠DCF
3. 如图,△ABC≌△DEF.若∠A=40°,∠CED=35°,则∠FEC的度数为 ( )
A. 25° B. 30° C. 35° D. 40°
4. (教材P43例1变式)如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的度数为 ( )
A. 40° B. 36° C. 30° D. 25°
5. 如图,在锐角三角形ABC中,AB=AC,AD是△ABC的角平分线,E是AD上一点,连接EB,EC.若∠EBC=45°,BC=6,则△EBC的面积为 ( )
A. 12 B. 9 C. 6 D. 以上都不对
6. (教材P50习题第6题变式)如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM.有下列结论:① △ABE≌△DBC;② ∠DMA=60°;③ △BPQ为等边三角形;④ MB平分∠AMC.其中,正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
7. (新考法·条件开放题)如图,点B,F,C,E在同一条直线上,AB∥ED,AC∥FD,要使△ABC≌△DEF,只需添加一个条件,则这个条件可以是 .
8. (2023·威海)如图,在正方形ABCD中,分别以点A,B为圆心,AB长为半径画弧,两弧交于点E,连接DE,则∠CDE的度数为 .
9. (整体思想)在△ABC中,AB,AC的垂直平分线分别交BC于点E,F.若∠BAC=115°,则∠EAF的度数为 .
10. 如图,在△ABC中,∠A=40°,∠B=∠C,BP=CE,BD=CP,则∠DPE的度数为 .
11. (分类讨论思想)如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP的长为 时,以A,P,Q三点构成的三角形与△ABC全等.
12. 如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是边BC上一动点,则DP长的最小值为 .
13. 如图,在△ABC中,∠C=90°,AC=BC,AD是△ABC的角平分线,过点B作BE⊥AD,交AD的延长线于点E.若BE=5,则AD的长为 .
14. (2025·苏州期末)如图,在△ABC中,边AB的垂直平分线l1与边BC相交于点D,边AC的垂直平分线l2与边BC相交于点E(点D在点E的左侧),连接AD,AE.若△ADE的周长为8,∠DAE=60°.求:
(1) BC的长;
(2) ∠BAC的度数.
第14题
15. (2024·宜宾改编)如图,E,F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1) 求证:CE=BF.
(2) 求∠BPC的度数.
(3) 过点B作BH⊥CE,垂足为H.若PF=1,PH=4,则CE的长为 .
第15题
16. (2024·苏州工业园区期中)如图,在△ABC中,M,N分别是BC与EF的中点,连接MN,CF⊥AB,BE⊥AC.
(1) 求证:MN⊥EF;
(2) 已知BC=8,当∠A=60°时,EF的长为 .
第16题
17. (2024·相城区期中改编)如图,O是等边三角形ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,已知∠AOB=110°,设∠BOC=α.
(1) 求证:△DOC是等边三角形;
(2) 当α=150°时,试判断△AOD的形状,并说明理由;
(3) 当α的度数为 时,△DOA是等腰三角形.
第17题
18. (2024·苏州工业园区期末)如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
(1) 若△ABC的面积为20,AB+CD=14,则AB-CD的值为 .
(2) 点E在边BC上,AE与CD相交于点F,且∠CEF=∠CFE.请你利用无刻度的直尺和圆规作出点E(不写作法,保留作图痕迹).
(3) 在(2)的条件下,延长AC至点G,连接GE,使GE=BE.若S△ABE=5S△CGE,求证:4BE=5CE.
第18题
期末复习专题
专题(一) 三 角 形
1. B 2. C 3. B 4. B 5. B 6. D 7. 答案不唯一,如AB=DE 8. 15° 9. 50° 10. 70° 11. 5或10 12. 4
13. 10 解析:如图,延长BE,AC交于点F.∵ AD是△ABC的角平分线,∴ ∠BAE=∠FAE.∵ BE⊥AD,∴ ∠AEB=∠AEF=90°.在△ABE和△AFE中,∴ △ABE≌△AFE(ASA),∴ BE=FE=5.∵ ∠AEF=90°,∴ ∠CAD+∠F=90°.∵ ∠ACD=90°,∴ ∠CBF+∠F=90°,∴ ∠CAD=∠CBF.在△ACD和△BCF中,∴ △ACD≌△BCF(ASA),∴ AD=BF=BE+FE=10.
14. (1) ∵ l1是边 AB的垂直平分线,∴ BD=AD.∵ l2是边 AC的垂直平分线,∴ AE=CE.∵ C△ADE=AD+AE+DE=8,∴ BC=BD+DE+CE=AD+DE+AE=8 (2) ∵ 在△ADE中,∠DAE=60°,∴ ∠ADE+∠AED=180°-60°=120°.由(1),得BD=AD,AE=CE,∴ ∠BAD=∠B,∠EAC=∠C.∵ ∠ADE=∠BAD+∠B,∠AED=∠EAC+∠C,∴ ∠BAD+∠EAC=(∠ADE+∠AED)=60°,∴ ∠BAC=∠BAD+∠EAC+∠DAE=60°+60°=120°
15. (1) ∵ △ABC是等边三角形,∴ BC=AB,∠A=∠EBC=60°.在△BCE和△ABF中, ∴ △BCE≌△ABF(SAS),∴ CE=BF (2) ∵ △BCE≌△ABF,∴ ∠BCE=∠ABF,∴ ∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,∴ 在△PBC中,∠BPC=180°-(∠PBC+∠PCB)=120° (3) 9
16. (1) 连接FM,EM.∵ CF⊥AB,BE⊥AC,∴ ∠CEB=∠CFB=90°.∵ M是BC的中点,∴ BM=FM=BC,CM=EM=BC,∴ FM=EM.∵ N是EF的中点,∴ MN⊥EF
(2) 4 解析:∵ △ABC的内角和为180°,∠A=60°,∴ ∠ABC+∠ACB=180°-∠A=120°.∵ BM=FM=BC=4,CM=EM=BC=4,∴ ∠ABC=∠BFM,∠ACB=∠CEM,∴ ∠BMF+∠CME=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(∠ABC+∠ACB)=360°-2×120°=120°,∴ ∠FME=180°-(∠BMF+∠CME)=60°.∵ FM=EM=4,∴ △EMF为等边三角形,∴ EF=EM=4.
17. (1) ∵ △ADC由△BOC绕点C按顺时针方向旋转60°得到,∴ ∠OCD=60°,CO=CD,∴ △OCD是等边三角形 (2) △AOD为直角三角形 理由:∵ △COD是等边三角形,∴ ∠ODC=60°.∵ △ADC由△BOC绕点C按顺时针方向旋转60°得到,∴ ∠ADC=∠BOC=α=150°,∴ ∠ADO=∠ADC-∠ODC=150°-60°=90°,∴ △AOD是直角三角形.
(3) 110°或125°或140° 解析:∵ △COD是等边三角形,∴ ∠DOC=∠ODC=60°,∴ ∠AOD=360°-110°-α-60°=190°-α.∵ △ADC由△BOC绕点C按顺时针方向旋转60°得到,∴ ∠ADC=∠BOC=α,∴ ∠ADO=∠ADC-∠ODC=α-60°.∵ △ADO的内角和为180°,∴ ∠OAD=180°-∠AOD-∠ADO=50°.① 当∠ADO=∠OAD,即α-60°=50°,α=110°时, OA=OD;② 当∠AOD=∠ADO,即190°-α=α-60°,α=125°时, OA=AD;③ 当∠AOD=∠OAD,即190°-α=50°,α=140°时,OD=AD.综上所述,当α的度数为110°或125°或140°时,△AOD是等腰三角形.
18. (1) 6 解析:∵ S△ABC=AB·CD=20,∴ AB·CD=40.∵ AB+CD=14,∴ AB-CD===6.
(2) 如图所示 解析:作∠CAB的平分线交BC,CD于点E,F.
(3) 如图,过点E作EH⊥AB于点H.由(2),得AE平分∠CAB,∴ ∠CAE=∠HAE.在△AEC和△AEH中, ∴ △AEC≌△AEH(AAS),∴ EC=EH,AC=AH.在Rt△ECG和Rt△EHB中,∴ Rt△ECG≌Rt△EHB(HL),∴ S△ECG=S△EHB.∵ S△ABE=5S△CGE,∴ S△ABE=5S△EHB,∴ AB=5BH,∴ AC=AH=4HB,∴ AC∶AB=4∶5.∵ ====,∴ 4BE=5CE
专题(一) 三 角 形
1. 在△ABC中,若AB=2,AC=4,且BC的长为整数,则△ABC的周长可能是 ( )
A. 8 B. 11 C. 12 D. 15
2. 如图,点D,E分别在△ABC的边上,连接AD,CE,DE,且AD,CE交于点F.若∠ACE=∠ACB,BC=2BD,则下列说法错误的是 ( )
A. AD是△ABC的中线 B. S△BDE=S△CDE
C. CE是△ADC的角平分线 D. ∠ACB=2∠DCF
3. 如图,△ABC≌△DEF.若∠A=40°,∠CED=35°,则∠FEC的度数为 ( )
A. 25° B. 30° C. 35° D. 40°
4. (教材P43例1变式)如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的度数为 ( )
A. 40° B. 36° C. 30° D. 25°
5. 如图,在锐角三角形ABC中,AB=AC,AD是△ABC的角平分线,E是AD上一点,连接EB,EC.若∠EBC=45°,BC=6,则△EBC的面积为 ( )
A. 12 B. 9 C. 6 D. 以上都不对
6. (教材P50习题第6题变式)如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM.有下列结论:① △ABE≌△DBC;② ∠DMA=60°;③ △BPQ为等边三角形;④ MB平分∠AMC.其中,正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
7. (新考法·条件开放题)如图,点B,F,C,E在同一条直线上,AB∥ED,AC∥FD,要使△ABC≌△DEF,只需添加一个条件,则这个条件可以是 .
8. (2023·威海)如图,在正方形ABCD中,分别以点A,B为圆心,AB长为半径画弧,两弧交于点E,连接DE,则∠CDE的度数为 .
9. (整体思想)在△ABC中,AB,AC的垂直平分线分别交BC于点E,F.若∠BAC=115°,则∠EAF的度数为 .
10. 如图,在△ABC中,∠A=40°,∠B=∠C,BP=CE,BD=CP,则∠DPE的度数为 .
11. (分类讨论思想)如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP的长为 时,以A,P,Q三点构成的三角形与△ABC全等.
12. 如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是边BC上一动点,则DP长的最小值为 .
13. 如图,在△ABC中,∠C=90°,AC=BC,AD是△ABC的角平分线,过点B作BE⊥AD,交AD的延长线于点E.若BE=5,则AD的长为 .
14. (2025·苏州期末)如图,在△ABC中,边AB的垂直平分线l1与边BC相交于点D,边AC的垂直平分线l2与边BC相交于点E(点D在点E的左侧),连接AD,AE.若△ADE的周长为8,∠DAE=60°.求:
(1) BC的长;
(2) ∠BAC的度数.
第14题
15. (2024·宜宾改编)如图,E,F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1) 求证:CE=BF.
(2) 求∠BPC的度数.
(3) 过点B作BH⊥CE,垂足为H.若PF=1,PH=4,则CE的长为 .
第15题
16. (2024·苏州工业园区期中)如图,在△ABC中,M,N分别是BC与EF的中点,连接MN,CF⊥AB,BE⊥AC.
(1) 求证:MN⊥EF;
(2) 已知BC=8,当∠A=60°时,EF的长为 .
第16题
17. (2024·相城区期中改编)如图,O是等边三角形ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,已知∠AOB=110°,设∠BOC=α.
(1) 求证:△DOC是等边三角形;
(2) 当α=150°时,试判断△AOD的形状,并说明理由;
(3) 当α的度数为 时,△DOA是等腰三角形.
第17题
18. (2024·苏州工业园区期末)如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
(1) 若△ABC的面积为20,AB+CD=14,则AB-CD的值为 .
(2) 点E在边BC上,AE与CD相交于点F,且∠CEF=∠CFE.请你利用无刻度的直尺和圆规作出点E(不写作法,保留作图痕迹).
(3) 在(2)的条件下,延长AC至点G,连接GE,使GE=BE.若S△ABE=5S△CGE,求证:4BE=5CE.
第18题
期末复习专题
专题(一) 三 角 形
1. B 2. C 3. B 4. B 5. B 6. D 7. 答案不唯一,如AB=DE 8. 15° 9. 50° 10. 70° 11. 5或10 12. 4
13. 10 解析:如图,延长BE,AC交于点F.∵ AD是△ABC的角平分线,∴ ∠BAE=∠FAE.∵ BE⊥AD,∴ ∠AEB=∠AEF=90°.在△ABE和△AFE中,∴ △ABE≌△AFE(ASA),∴ BE=FE=5.∵ ∠AEF=90°,∴ ∠CAD+∠F=90°.∵ ∠ACD=90°,∴ ∠CBF+∠F=90°,∴ ∠CAD=∠CBF.在△ACD和△BCF中,∴ △ACD≌△BCF(ASA),∴ AD=BF=BE+FE=10.
14. (1) ∵ l1是边 AB的垂直平分线,∴ BD=AD.∵ l2是边 AC的垂直平分线,∴ AE=CE.∵ C△ADE=AD+AE+DE=8,∴ BC=BD+DE+CE=AD+DE+AE=8 (2) ∵ 在△ADE中,∠DAE=60°,∴ ∠ADE+∠AED=180°-60°=120°.由(1),得BD=AD,AE=CE,∴ ∠BAD=∠B,∠EAC=∠C.∵ ∠ADE=∠BAD+∠B,∠AED=∠EAC+∠C,∴ ∠BAD+∠EAC=(∠ADE+∠AED)=60°,∴ ∠BAC=∠BAD+∠EAC+∠DAE=60°+60°=120°
15. (1) ∵ △ABC是等边三角形,∴ BC=AB,∠A=∠EBC=60°.在△BCE和△ABF中, ∴ △BCE≌△ABF(SAS),∴ CE=BF (2) ∵ △BCE≌△ABF,∴ ∠BCE=∠ABF,∴ ∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,∴ 在△PBC中,∠BPC=180°-(∠PBC+∠PCB)=120° (3) 9
16. (1) 连接FM,EM.∵ CF⊥AB,BE⊥AC,∴ ∠CEB=∠CFB=90°.∵ M是BC的中点,∴ BM=FM=BC,CM=EM=BC,∴ FM=EM.∵ N是EF的中点,∴ MN⊥EF
(2) 4 解析:∵ △ABC的内角和为180°,∠A=60°,∴ ∠ABC+∠ACB=180°-∠A=120°.∵ BM=FM=BC=4,CM=EM=BC=4,∴ ∠ABC=∠BFM,∠ACB=∠CEM,∴ ∠BMF+∠CME=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(∠ABC+∠ACB)=360°-2×120°=120°,∴ ∠FME=180°-(∠BMF+∠CME)=60°.∵ FM=EM=4,∴ △EMF为等边三角形,∴ EF=EM=4.
17. (1) ∵ △ADC由△BOC绕点C按顺时针方向旋转60°得到,∴ ∠OCD=60°,CO=CD,∴ △OCD是等边三角形 (2) △AOD为直角三角形 理由:∵ △COD是等边三角形,∴ ∠ODC=60°.∵ △ADC由△BOC绕点C按顺时针方向旋转60°得到,∴ ∠ADC=∠BOC=α=150°,∴ ∠ADO=∠ADC-∠ODC=150°-60°=90°,∴ △AOD是直角三角形.
(3) 110°或125°或140° 解析:∵ △COD是等边三角形,∴ ∠DOC=∠ODC=60°,∴ ∠AOD=360°-110°-α-60°=190°-α.∵ △ADC由△BOC绕点C按顺时针方向旋转60°得到,∴ ∠ADC=∠BOC=α,∴ ∠ADO=∠ADC-∠ODC=α-60°.∵ △ADO的内角和为180°,∴ ∠OAD=180°-∠AOD-∠ADO=50°.① 当∠ADO=∠OAD,即α-60°=50°,α=110°时, OA=OD;② 当∠AOD=∠ADO,即190°-α=α-60°,α=125°时, OA=AD;③ 当∠AOD=∠OAD,即190°-α=50°,α=140°时,OD=AD.综上所述,当α的度数为110°或125°或140°时,△AOD是等腰三角形.
18. (1) 6 解析:∵ S△ABC=AB·CD=20,∴ AB·CD=40.∵ AB+CD=14,∴ AB-CD===6.
(2) 如图所示 解析:作∠CAB的平分线交BC,CD于点E,F.
(3) 如图,过点E作EH⊥AB于点H.由(2),得AE平分∠CAB,∴ ∠CAE=∠HAE.在△AEC和△AEH中, ∴ △AEC≌△AEH(AAS),∴ EC=EH,AC=AH.在Rt△ECG和Rt△EHB中,∴ Rt△ECG≌Rt△EHB(HL),∴ S△ECG=S△EHB.∵ S△ABE=5S△CGE,∴ S△ABE=5S△EHB,∴ AB=5BH,∴ AC=AH=4HB,∴ AC∶AB=4∶5.∵ ====,∴ 4BE=5CE
同课章节目录
