期末复习专题 专题(三) 勾股定理 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 期末复习专题 专题(三) 勾股定理 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 137.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 22:12:07 | ||
图片预览

文档简介
期末复习专题 专题(三) 勾股定理
1.
下列各组数据中的三个数作为三角形的边长,能构成直角三角形的一组是 ( )
A. ,, B. 1,, C. 6,7,8 D. 2,3,4
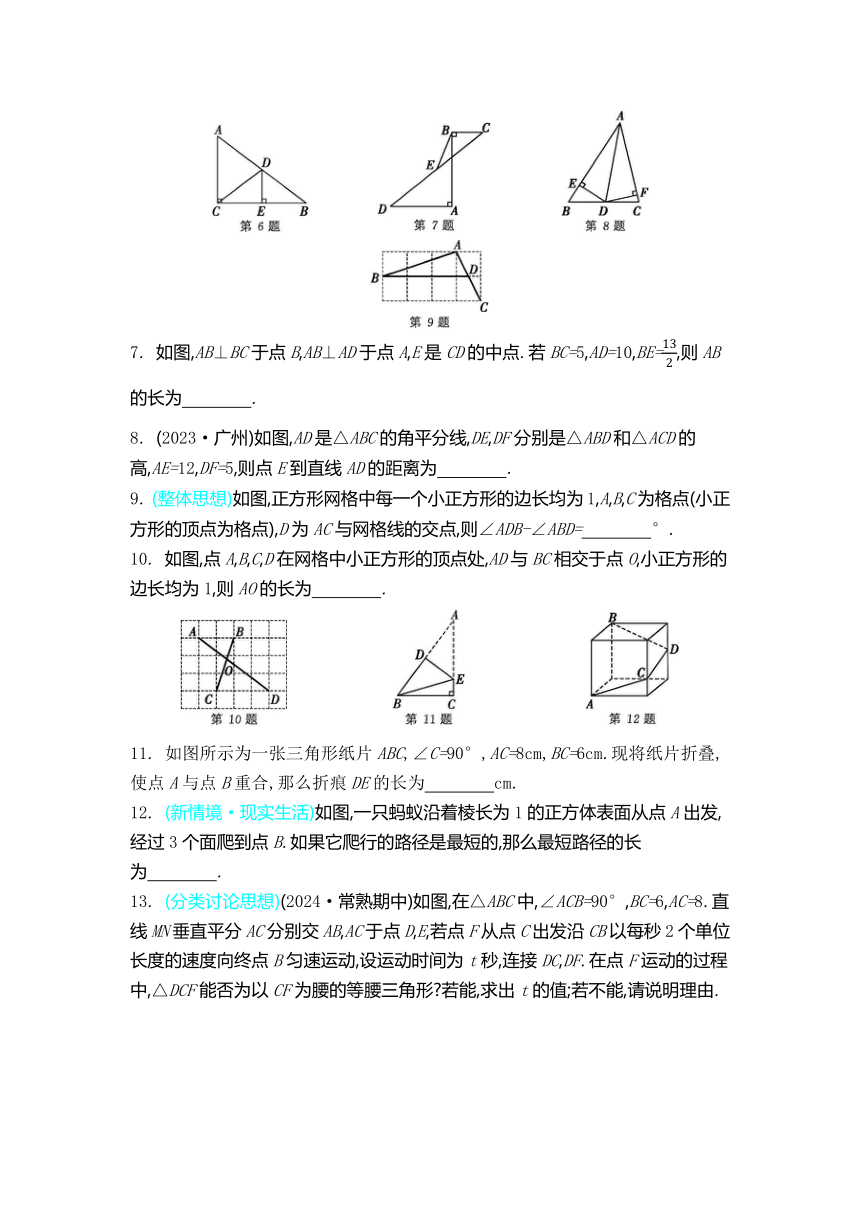
2. 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE∥AB,交AC于点E,DF⊥AB于点F,DE=5,DF=3,则下列结论错误的是 ( )
A. BF=1 B. DC=3 C. AE=5 D. AC=9
3. (分类讨论思想)在△ABC中,AB=15,AC=13,边BC上的高AD=12,则BC的长为 ( )
A. 5 B. 14 C. 4或14 D. 9或14
4. 如图,点E在△DBC的边DB上,点A在△DBC的内部,∠DAE=∠BAC=90°,AD=AE,AB=AC,连接CE.给出下列结论:① BD=CE;② ∠ABD+∠ECB=45°;③ BD⊥CE;④ BE2=2(AD2+AB2)-CD2.其中,所有正确的结论是 ( )
A. ①②③④ B. ②④ C. ①②③ D. ①③④
5. (新考法·探究题)有一道题目如下:如图,∠B=45°,BC=2,在射线BM上取一点A,设AC=d,若对于d的一个数值,只能作出唯一一个△ABC,求d的取值范围.对于其答案,甲:d≥2;乙:d=1.6;丙:d=.下列说法正确的是 ( )
A. 只有甲的答案正确 B. 甲、丙的答案合在一起才正确
C. 甲、乙的答案合在一起才正确 D. 三人的答案合在一起才正确
6. (2023·荆州改编)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过点D作DE⊥BC,垂足为E,连接CD.若CD=5,BC=8,则DE的长为 .
7. 如图,AB⊥BC于点B,AB⊥AD于点A,E是CD的中点.若BC=5,AD=10,BE=,则AB的长为 .
8. (2023·广州)如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,AE=12,DF=5,则点E到直线AD的距离为 .
9. (整体思想)如图,正方形网格中每一个小正方形的边长均为1,A,B,C为格点(小正方形的顶点为格点),D为AC与网格线的交点,则∠ADB-∠ABD= °.
10. 如图,点A,B,C,D在网格中小正方形的顶点处,AD与BC相交于点O,小正方形的边长均为1,则AO的长为 .
11. 如图所示为一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠,使点A与点B重合,那么折痕DE的长为 cm.
12. (新情境·现实生活)如图,一只蚂蚁沿着棱长为1的正方体表面从点A出发,经过3个面爬到点B.如果它爬行的路径是最短的,那么最短路径的长为 .
13. (分类讨论思想)(2024·常熟期中)如图,在△ABC中,∠ACB=90°,BC=6,AC=8.直线MN垂直平分AC分别交AB,AC于点D,E,若点F从点C出发沿CB以每秒2个单位长度的速度向终点B匀速运动,设运动时间为t秒,连接DC,DF.在点F运动的过程中,△DCF能否为以CF为腰的等腰三角形 若能,求出t的值;若不能,请说明理由.
第13题
14. 如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC的中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1) 线段BH与CA相等吗 若相等,请给予证明;若不相等,请说明理由.
(2) 求证:BG2-GE2=EA2.
第14题
专题(三) 勾股定理
1. B 2. A 3. C 4. A
5. B 解析:根据题意,得当AC⊥AB或AC≥BC时,能作出唯一的△ABC.当AC⊥AB时,易得d=;当AC≥BC时,d≥2.∴ 甲、丙的答案合在一起才正确.
6. 3 7. 12 8. 9. 45
10. 2 解析:如图,连接AE,ED.由勾股定理,易得AD=5.∵ DE=5,∴ AD=DE,∴ ∠DAE=∠DEA.由网格的特征,得AE∥BC,∴ ∠DAE=∠DOC,∠DEA=∠DCO,∴ ∠DOC=∠DCO,∴ DO=DC=3,∴ AO=AD-DO=5-3=2.
11. 12.
13. 能 由题意,得CF=2t.∵ ∠ACB=90°,BC=6,AC=8,∴ AB==10.∵ 直线MN垂直平分AC,∴ DA=DC,∴ ∠DCA=∠A.∵ ∠ACB=90°,∴ ∠A+∠B=90°,∠BCD+∠DCA=90°,∴ ∠B=∠BCD,∴ BD=DC,∴ BD=DC=AD=AB=5.① 当CF=CD时,由2t=5,得t=;② 当CF=DF=2t时,如图,过点D作DH⊥BC于点H,则易得△DHC≌△CED,∴ DH=CE=AC=4.∵ 在Rt△CDH中,CH==3,∴ FH=2t-3.∵ 在Rt△FDH中,DF2=FH2+DH2,∴ (2t)2=(2t-3)2+42,解得t=.综上所述,t的值为或
14. (1) 相等 ∵ CD⊥AB,BE⊥AC,∴ ∠BDC=∠CDA=∠BEA=90°,∴ ∠A+∠DCA=90°,∠A+∠ABE=90°,∴ ∠ABE=∠DCA.又∵ ∠ABC=45°,∴ 易得∠BCD=∠ABC=45°,∴ DC=DB.在△DBH和△DCA中,∴ △DBH≌△DCA,∴ BH=CA (2) 如图,连接CG.∵ F为BC的中点,DB=DC,∴ DF垂直平分BC,∴ BG=CG.∵ BE⊥AC,∴ ∠BEA=∠BEC=90°.在△ABE和△CBE中, ∴ △ABE≌△CBE,∴ EA=EC.∵ 在Rt△CGE中,由勾股定理,得CG2-GE2=EC2,∴ BG2-GE2=EA2
1.
下列各组数据中的三个数作为三角形的边长,能构成直角三角形的一组是 ( )
A. ,, B. 1,, C. 6,7,8 D. 2,3,4
2. 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE∥AB,交AC于点E,DF⊥AB于点F,DE=5,DF=3,则下列结论错误的是 ( )
A. BF=1 B. DC=3 C. AE=5 D. AC=9
3. (分类讨论思想)在△ABC中,AB=15,AC=13,边BC上的高AD=12,则BC的长为 ( )
A. 5 B. 14 C. 4或14 D. 9或14
4. 如图,点E在△DBC的边DB上,点A在△DBC的内部,∠DAE=∠BAC=90°,AD=AE,AB=AC,连接CE.给出下列结论:① BD=CE;② ∠ABD+∠ECB=45°;③ BD⊥CE;④ BE2=2(AD2+AB2)-CD2.其中,所有正确的结论是 ( )
A. ①②③④ B. ②④ C. ①②③ D. ①③④
5. (新考法·探究题)有一道题目如下:如图,∠B=45°,BC=2,在射线BM上取一点A,设AC=d,若对于d的一个数值,只能作出唯一一个△ABC,求d的取值范围.对于其答案,甲:d≥2;乙:d=1.6;丙:d=.下列说法正确的是 ( )
A. 只有甲的答案正确 B. 甲、丙的答案合在一起才正确
C. 甲、乙的答案合在一起才正确 D. 三人的答案合在一起才正确
6. (2023·荆州改编)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过点D作DE⊥BC,垂足为E,连接CD.若CD=5,BC=8,则DE的长为 .
7. 如图,AB⊥BC于点B,AB⊥AD于点A,E是CD的中点.若BC=5,AD=10,BE=,则AB的长为 .
8. (2023·广州)如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,AE=12,DF=5,则点E到直线AD的距离为 .
9. (整体思想)如图,正方形网格中每一个小正方形的边长均为1,A,B,C为格点(小正方形的顶点为格点),D为AC与网格线的交点,则∠ADB-∠ABD= °.
10. 如图,点A,B,C,D在网格中小正方形的顶点处,AD与BC相交于点O,小正方形的边长均为1,则AO的长为 .
11. 如图所示为一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠,使点A与点B重合,那么折痕DE的长为 cm.
12. (新情境·现实生活)如图,一只蚂蚁沿着棱长为1的正方体表面从点A出发,经过3个面爬到点B.如果它爬行的路径是最短的,那么最短路径的长为 .
13. (分类讨论思想)(2024·常熟期中)如图,在△ABC中,∠ACB=90°,BC=6,AC=8.直线MN垂直平分AC分别交AB,AC于点D,E,若点F从点C出发沿CB以每秒2个单位长度的速度向终点B匀速运动,设运动时间为t秒,连接DC,DF.在点F运动的过程中,△DCF能否为以CF为腰的等腰三角形 若能,求出t的值;若不能,请说明理由.
第13题
14. 如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC的中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1) 线段BH与CA相等吗 若相等,请给予证明;若不相等,请说明理由.
(2) 求证:BG2-GE2=EA2.
第14题
专题(三) 勾股定理
1. B 2. A 3. C 4. A
5. B 解析:根据题意,得当AC⊥AB或AC≥BC时,能作出唯一的△ABC.当AC⊥AB时,易得d=;当AC≥BC时,d≥2.∴ 甲、丙的答案合在一起才正确.
6. 3 7. 12 8. 9. 45
10. 2 解析:如图,连接AE,ED.由勾股定理,易得AD=5.∵ DE=5,∴ AD=DE,∴ ∠DAE=∠DEA.由网格的特征,得AE∥BC,∴ ∠DAE=∠DOC,∠DEA=∠DCO,∴ ∠DOC=∠DCO,∴ DO=DC=3,∴ AO=AD-DO=5-3=2.
11. 12.
13. 能 由题意,得CF=2t.∵ ∠ACB=90°,BC=6,AC=8,∴ AB==10.∵ 直线MN垂直平分AC,∴ DA=DC,∴ ∠DCA=∠A.∵ ∠ACB=90°,∴ ∠A+∠B=90°,∠BCD+∠DCA=90°,∴ ∠B=∠BCD,∴ BD=DC,∴ BD=DC=AD=AB=5.① 当CF=CD时,由2t=5,得t=;② 当CF=DF=2t时,如图,过点D作DH⊥BC于点H,则易得△DHC≌△CED,∴ DH=CE=AC=4.∵ 在Rt△CDH中,CH==3,∴ FH=2t-3.∵ 在Rt△FDH中,DF2=FH2+DH2,∴ (2t)2=(2t-3)2+42,解得t=.综上所述,t的值为或
14. (1) 相等 ∵ CD⊥AB,BE⊥AC,∴ ∠BDC=∠CDA=∠BEA=90°,∴ ∠A+∠DCA=90°,∠A+∠ABE=90°,∴ ∠ABE=∠DCA.又∵ ∠ABC=45°,∴ 易得∠BCD=∠ABC=45°,∴ DC=DB.在△DBH和△DCA中,∴ △DBH≌△DCA,∴ BH=CA (2) 如图,连接CG.∵ F为BC的中点,DB=DC,∴ DF垂直平分BC,∴ BG=CG.∵ BE⊥AC,∴ ∠BEA=∠BEC=90°.在△ABE和△CBE中, ∴ △ABE≌△CBE,∴ EA=EC.∵ 在Rt△CGE中,由勾股定理,得CG2-GE2=EC2,∴ BG2-GE2=EA2
同课章节目录
