5.1 变量与函数 同步练 (含2课时,含答案)2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 5.1 变量与函数 同步练 (含2课时,含答案)2025-2026学年数学苏科版(2024)八年级上册 | 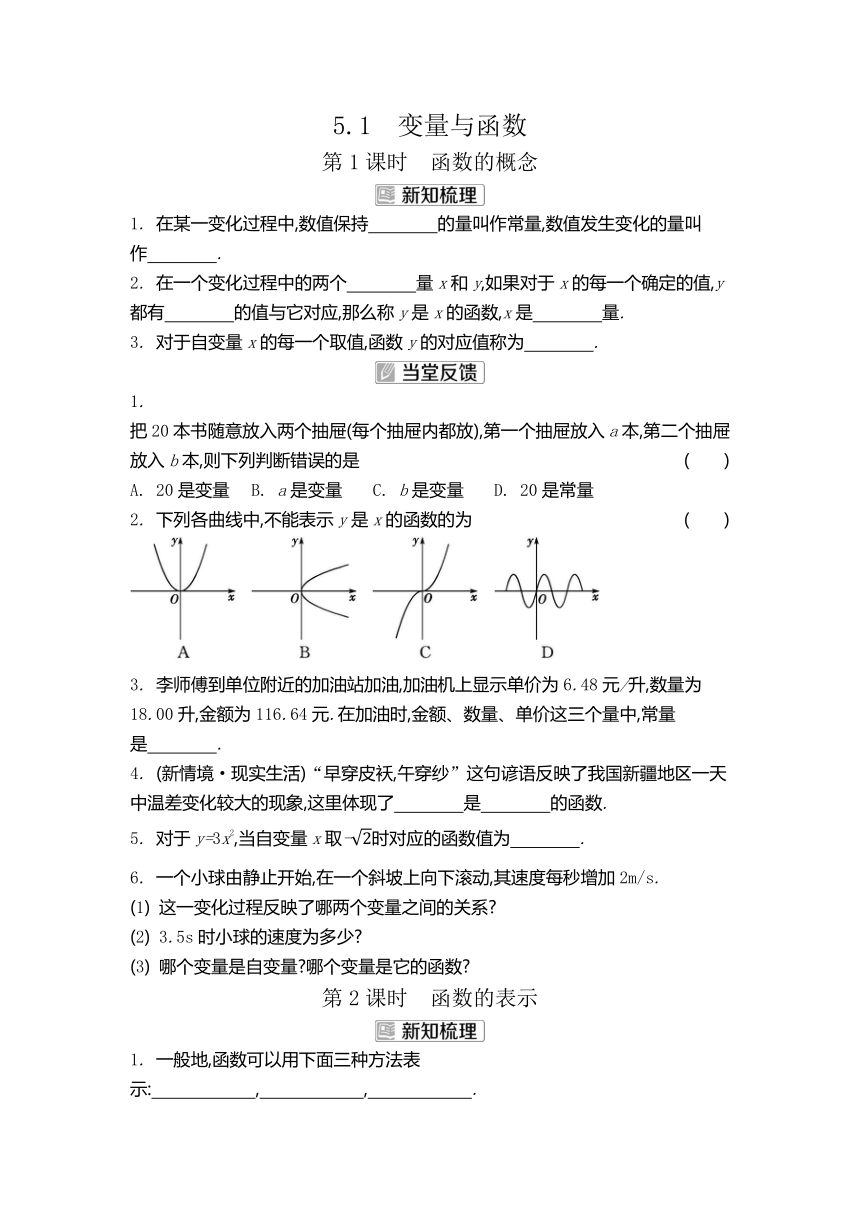 | |
| 格式 | docx | ||
| 文件大小 | 63.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 12:10:01 | ||
图片预览

文档简介
5.1 变量与函数
第1课时 函数的概念
1. 在某一变化过程中,数值保持 的量叫作常量,数值发生变化的量叫作 .
2. 在一个变化过程中的两个 量x和y,如果对于x的每一个确定的值,y都有 的值与它对应,那么称y是x的函数,x是 量.
3. 对于自变量x的每一个取值,函数y的对应值称为 .
1.
把20本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入a本,第二个抽屉放入b本,则下列判断错误的是 ( )
A. 20是变量 B. a是变量 C. b是变量 D. 20是常量
2. 下列各曲线中,不能表示y是x的函数的为 ( )
3. 李师傅到单位附近的加油站加油,加油机上显示单价为6.48元/升,数量为18.00升,金额为116.64元.在加油时,金额、数量、单价这三个量中,常量是 .
4. (新情境·现实生活)“早穿皮袄,午穿纱”这句谚语反映了我国新疆地区一天中温差变化较大的现象,这里体现了 是 的函数.
5. 对于y=3x2,当自变量x取-时对应的函数值为 .
6. 一个小球由静止开始,在一个斜坡上向下滚动,其速度每秒增加2m/s.
(1) 这一变化过程反映了哪两个变量之间的关系
(2) 3.5s时小球的速度为多少
(3) 哪个变量是自变量 哪个变量是它的函数
第2课时 函数的表示
1. 一般地,函数可以用下面三种方法表示: , , .
2. 用 和 组成的表示函数的表达式叫作函数表达式.在实际问题中,自变量的取值通常有一定的范围.
3. 把自变量的取值作为 坐标,对应的函数值作为 坐标,在平面直角坐标系中描出对应的点,这些点组成的图形叫作函数的图象.
1. (2024·海南)设直角三角形中一个锐角为x°(0
A. y=180+x B. y=180-x C. y=90+x D. y=90-x
2. 某城市市区有x万人,市区绿地面积为50万平方米,平均每人拥有绿地y平方米,则y与x之间的函数表达式为 .
3. 某商场销售一种饮料,在进价的基础上增加相同比例的利润组成售价y(元).设销量为x瓶,y与x之间的部分对应值如下表:
x/瓶 1 2 3 4 …
y/元 5+0.4 10+0.8 15+1.2 20+1.6 …
y与x之间的函数表达式为 ,x的取值范围是 .
4. (2023·自贡改编)如图①,小亮家、报亭、羽毛球馆在同一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮到家的距离y(km)与时间x(min)之间的关系如图②所示.
(1) 小亮从家到羽毛球馆用了 min,报亭到小亮家的距离是 m;
(2) 小亮打羽毛球的时间是 min;
(3) 小亮从羽毛球馆到报亭的平均速度为 m/min.
5.1 变量与函数
第1课时 函数的概念
1. 不变 变量 2. 变 唯一 自变 3. 函数值
1. A 2. B 3. 单价 4. 气温 时间 5. 6
6. (1) 速度和时间 (2) 7m/s (3) 时间是自变量 速度是时间的函数
第2课时 函数的表示
1. 用表达式表示 用表格表示 用图象表示 2. 自变量 常量 3. 横 纵
1. D 2. y=(x>0) 3. y=5.4x 正整数
4. (1) 7 400 (2) 30
(3) 75 解析:小亮从羽毛球馆到报亭的平均速度为(1.0-0.4)÷(45-37)=0.075(km/min)=75(m/min).
第1课时 函数的概念
1. 在某一变化过程中,数值保持 的量叫作常量,数值发生变化的量叫作 .
2. 在一个变化过程中的两个 量x和y,如果对于x的每一个确定的值,y都有 的值与它对应,那么称y是x的函数,x是 量.
3. 对于自变量x的每一个取值,函数y的对应值称为 .
1.
把20本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入a本,第二个抽屉放入b本,则下列判断错误的是 ( )
A. 20是变量 B. a是变量 C. b是变量 D. 20是常量
2. 下列各曲线中,不能表示y是x的函数的为 ( )
3. 李师傅到单位附近的加油站加油,加油机上显示单价为6.48元/升,数量为18.00升,金额为116.64元.在加油时,金额、数量、单价这三个量中,常量是 .
4. (新情境·现实生活)“早穿皮袄,午穿纱”这句谚语反映了我国新疆地区一天中温差变化较大的现象,这里体现了 是 的函数.
5. 对于y=3x2,当自变量x取-时对应的函数值为 .
6. 一个小球由静止开始,在一个斜坡上向下滚动,其速度每秒增加2m/s.
(1) 这一变化过程反映了哪两个变量之间的关系
(2) 3.5s时小球的速度为多少
(3) 哪个变量是自变量 哪个变量是它的函数
第2课时 函数的表示
1. 一般地,函数可以用下面三种方法表示: , , .
2. 用 和 组成的表示函数的表达式叫作函数表达式.在实际问题中,自变量的取值通常有一定的范围.
3. 把自变量的取值作为 坐标,对应的函数值作为 坐标,在平面直角坐标系中描出对应的点,这些点组成的图形叫作函数的图象.
1. (2024·海南)设直角三角形中一个锐角为x°(0
A. y=180+x B. y=180-x C. y=90+x D. y=90-x
2. 某城市市区有x万人,市区绿地面积为50万平方米,平均每人拥有绿地y平方米,则y与x之间的函数表达式为 .
3. 某商场销售一种饮料,在进价的基础上增加相同比例的利润组成售价y(元).设销量为x瓶,y与x之间的部分对应值如下表:
x/瓶 1 2 3 4 …
y/元 5+0.4 10+0.8 15+1.2 20+1.6 …
y与x之间的函数表达式为 ,x的取值范围是 .
4. (2023·自贡改编)如图①,小亮家、报亭、羽毛球馆在同一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮到家的距离y(km)与时间x(min)之间的关系如图②所示.
(1) 小亮从家到羽毛球馆用了 min,报亭到小亮家的距离是 m;
(2) 小亮打羽毛球的时间是 min;
(3) 小亮从羽毛球馆到报亭的平均速度为 m/min.
5.1 变量与函数
第1课时 函数的概念
1. 不变 变量 2. 变 唯一 自变 3. 函数值
1. A 2. B 3. 单价 4. 气温 时间 5. 6
6. (1) 速度和时间 (2) 7m/s (3) 时间是自变量 速度是时间的函数
第2课时 函数的表示
1. 用表达式表示 用表格表示 用图象表示 2. 自变量 常量 3. 横 纵
1. D 2. y=(x>0) 3. y=5.4x 正整数
4. (1) 7 400 (2) 30
(3) 75 解析:小亮从羽毛球馆到报亭的平均速度为(1.0-0.4)÷(45-37)=0.075(km/min)=75(m/min).
同课章节目录
