1.3 全等三角形的判定 同步练 (含6课时,含答案)2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 1.3 全等三角形的判定 同步练 (含6课时,含答案)2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 458.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 12:29:43 | ||
图片预览

文档简介
1.3 全等三角形的判定
第1课时 “边角边”
两边及其 分别相等的两个三角形全等(简写成“边角边”或“ ”).
1. (教材P17例2变式)如图,在△ABD和△ACE中,AB=AC,AD=AE.若要用“SAS”判定△ABD≌△ACE,则可补充的条件是 ( )
A. ∠B=∠C B. ∠D=∠E C. ∠BAD=∠CAE D. ∠B=∠E
2.
(2023·福建改编)如图,AB=AC,AD=AE,∠BAC=∠DAE,则下列结论错误的是 ( )
A. ∠BAD=∠CAE B. △ABD≌△ACE
C. AB=BC D. BD=CE
3. 如图,有下列条件:① BC=AD,∠ABC=∠BAD;② BC=AD,AC=BD;③ BC=AD,∠CAB=∠DBA;④ AC=BD,∠BAC=∠ABD.其中,能用“SAS”判定△ABC≌△BAD的是 (填序号).
4. 如图,点B,E,C,F在同一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF的长为 .
5. (2024·南通)如图,点D在△ABC的边AB上,DF经过边AC的中点E,且EF=DE.
求证:CF∥AB.
第5题
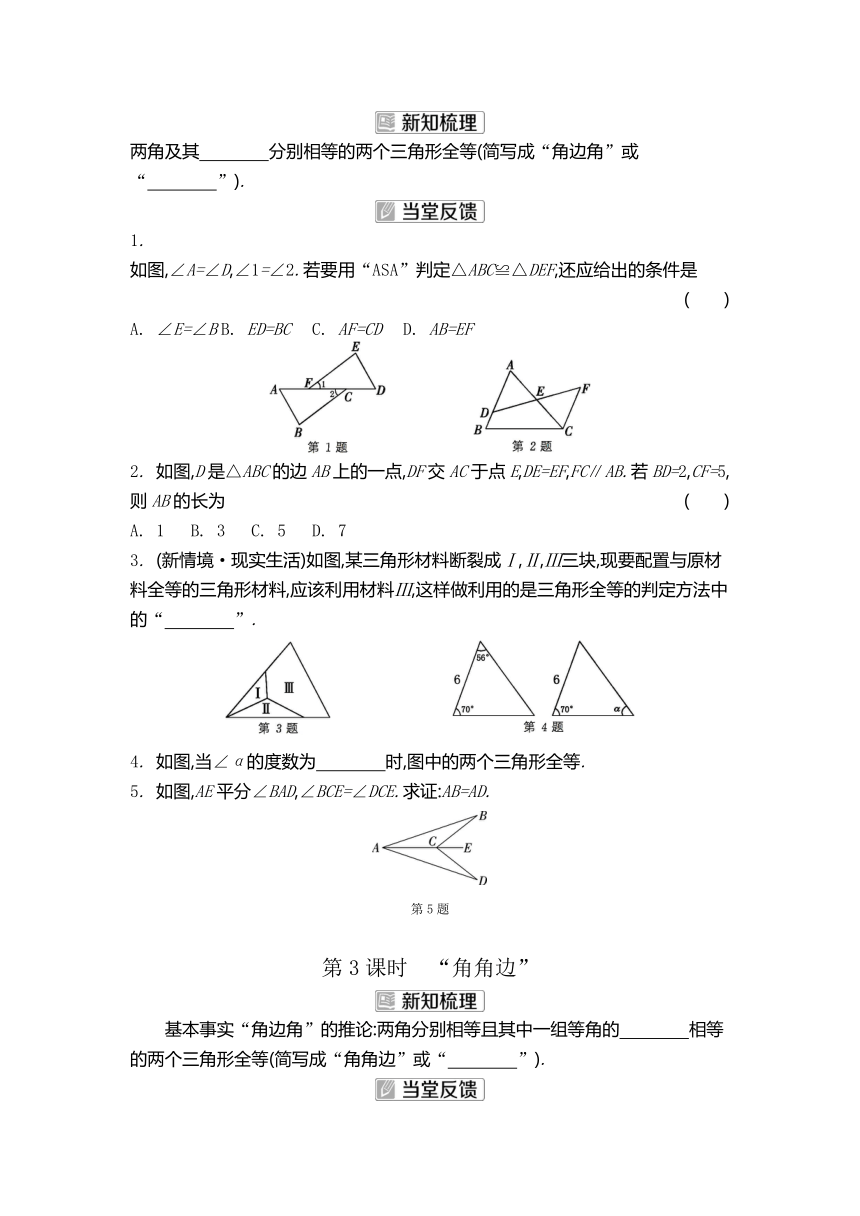
第2课时 “角边角”
两角及其 分别相等的两个三角形全等(简写成“角边角”或“ ”).
1.
如图,∠A=∠D,∠1=∠2.若要用“ASA”判定△ABC≌△DEF,还应给出的条件是 ( )
A. ∠E=∠B B. ED=BC C. AF=CD D. AB=EF
2. 如图,D是△ABC的边AB上的一点,DF交AC于点E,DE=EF,FC∥AB.若BD=2,CF=5,则AB的长为 ( )
A. 1 B. 3 C. 5 D. 7
3. (新情境·现实生活)如图,某三角形材料断裂成Ⅰ,Ⅱ,Ⅲ三块,现要配置与原材料全等的三角形材料,应该利用材料Ⅲ,这样做利用的是三角形全等的判定方法中的“ ”.
4. 如图,当∠α的度数为 时,图中的两个三角形全等.
5. 如图,AE平分∠BAD,∠BCE=∠DCE.求证:AB=AD.
第5题
第3课时 “角角边”
基本事实“角边角”的推论:两角分别相等且其中一组等角的 相等的两个三角形全等(简写成“角角边”或“ ”).
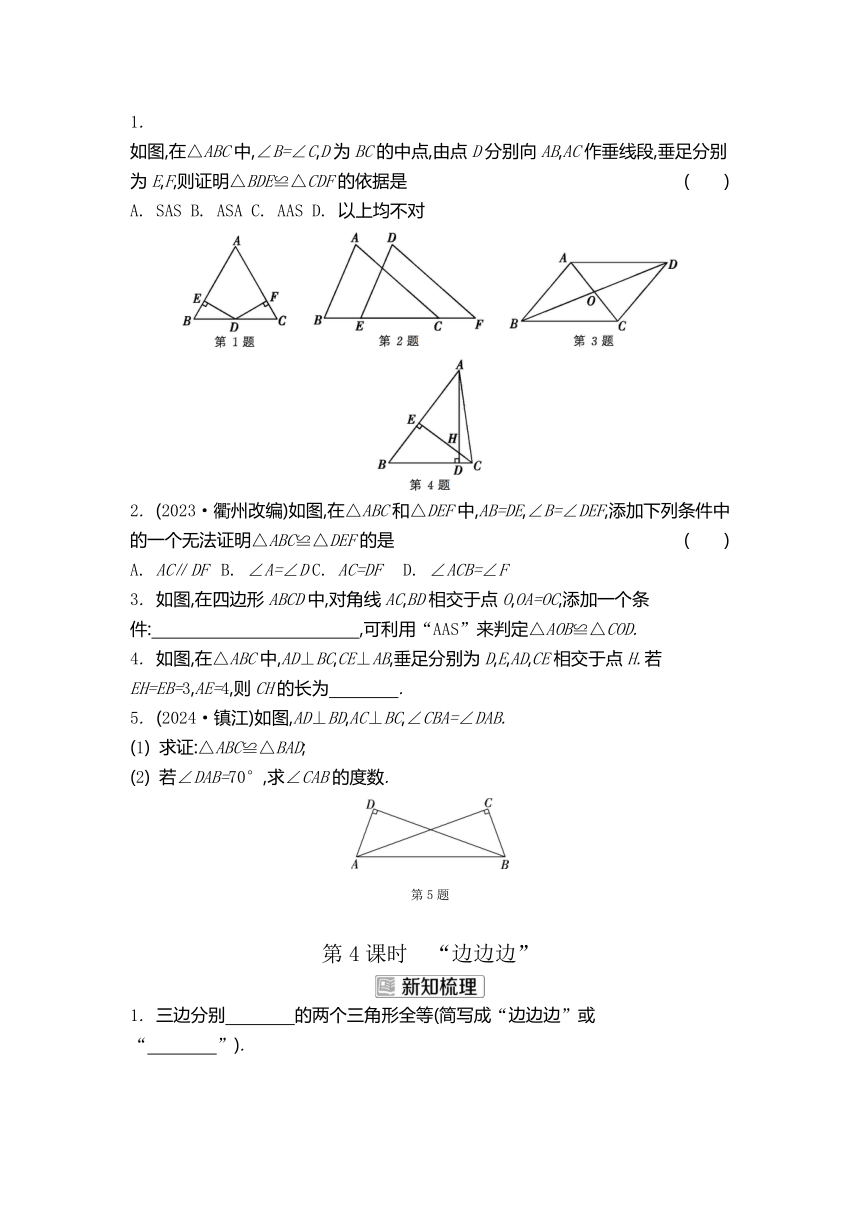
1.
如图,在△ABC中,∠B=∠C,D为BC的中点,由点D分别向AB,AC作垂线段,垂足分别为E,F,则证明△BDE≌△CDF的依据是 ( )
A. SAS B. ASA C. AAS D. 以上均不对
2. (2023·衢州改编)如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列条件中的一个无法证明△ABC≌△DEF的是 ( )
A. AC∥DF B. ∠A=∠D C. AC=DF D. ∠ACB=∠F
3. 如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,添加一个条件: ,可利用“AAS”来判定△AOB≌△COD.
4. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于点H.若EH=EB=3,AE=4,则CH的长为 .
5. (2024·镇江)如图,AD⊥BD,AC⊥BC,∠CBA=∠DAB.
(1) 求证:△ABC≌△BAD;
(2) 若∠DAB=70°,求∠CAB的度数.
第5题
第4课时 “边边边”
1. 三边分别 的两个三角形全等(简写成“边边边”或“ ”).
2. 如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定,三角形的这个性质叫作三角形的 性.
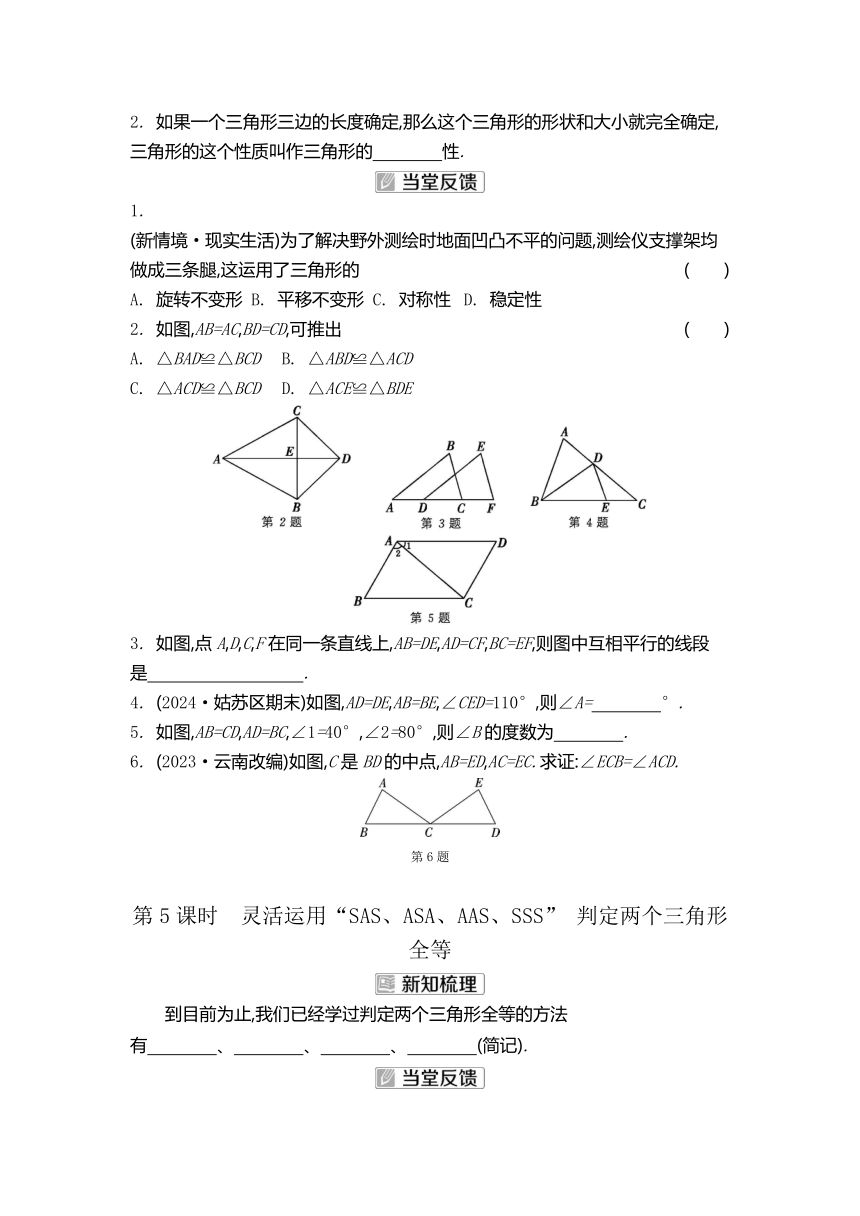
1.
(新情境·现实生活)为了解决野外测绘时地面凹凸不平的问题,测绘仪支撑架均做成三条腿,这运用了三角形的 ( )
A. 旋转不变形 B. 平移不变形 C. 对称性 D. 稳定性
2. 如图,AB=AC,BD=CD,可推出 ( )
A. △BAD≌△BCD B. △ABD≌△ACD
C. △ACD≌△BCD D. △ACE≌△BDE
3. 如图,点A,D,C,F在同一条直线上,AB=DE,AD=CF,BC=EF,则图中互相平行的线段是 .
4. (2024·姑苏区期末)如图,AD=DE,AB=BE,∠CED=110°,则∠A= °.
5. 如图,AB=CD,AD=BC,∠1=40°,∠2=80°,则∠B的度数为 .
6. (2023·云南改编)如图,C是BD的中点,AB=ED,AC=EC.求证:∠ECB=∠ACD.
第6题
第5课时 灵活运用“SAS、ASA、AAS、SSS” 判定两个三角形全等
到目前为止,我们已经学过判定两个三角形全等的方法有 、 、 、 (简记).
1.
如图,下列各组条件中,能用“SAS”或“ASA”或“AAS”判定△ABC≌△DEF的是 ( )
A. AB=DE,AC=DF,∠C=∠F B. AB=DE,∠A=∠D,BC=EF
C. AC=DF,∠A=∠D,BC=EF D. AC=DF,∠C=∠F,BC=EF
2. 如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB,则下列结论正确的是 ( )
A. ∠A=∠C B. ∠A=∠E
C. AC=DE D. B是AD的中点
3. (2024·牡丹江)如图,在△ABC中,D是AB上一点,CF∥AB,D,E,F三点共线,请添加一个条件: ,使得AE=CE(写出一种即可).
4. 如图,AD是△ABC的角平分线.若∠B=90°,BD=3,则点D到AC的距离是 .
5. 如图,AB=CB,要说明△ABE≌△CBD.
如果直接利用“ASA”,那么要补充的条件是 ;
如果直接利用“AAS”,那么要补充的条件是 ;
如果直接利用“SAS”,那么要补充的条件是 .
6. 如图,在△ABC中,AB=5,AC=3,AD是△ABC的中线,设AD的长为m.延长AD到点E,使DE=AD,连接BE.由“SAS”可证得△ACD≌△ ,因此 =AC=3.在△ABE中,根据三角形三边的不等关系,可得AE长度的取值范围是 ,从而得到△ABC的中线AD长度的取值范围是 ,即m的取值范围是 .
7. (教材P22例4变式)如图,△ABC≌△A'B'C',AD,A'D'分别是△ABC与△A'B'C'的角平分线.求证:AD=A'D'.
8. 如图,在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.
第8题
9. 如图,AC,BD相交于点O,且AB=CD,AC=DB.求证:
(1) ∠A=∠D;
(2) AO=DO.
第9题
第6课时 直角三角形全等的判定
1. 直角三角形是特殊的三角形,可以用符号“ ”表示.
2. 斜边和 分别相等的两个直角三角形全等(简写成“ ”).
1.
判定两个直角三角形全等的条件可以是 ( )
A. 一锐角对应相等 B. 两锐角对应相等
C. 一条边对应相等 D. 两条边对应相等
2. 如图,在四边形ABCD中,AC与BD相交于点O,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F,连接CE,AF,则图中与AO长度相等的线段是 ( )
A. AD B. DO C. CO D. BO
3. 如图,AB⊥CD,且AB=CD,CE⊥AD,BF⊥AD,垂足分别为E,F,且满足CE=AF.若AE=4,BF=6,则AD的长为 .
4. 如图,在△ABC中,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF的度数为 .
5. (2023·南通)如图,点D,E分别在AB,AC上,∠ADC=∠AEB=90°,BE,CD相交于点O,OB=OC,连接AO.求证:∠1=∠2.
第5题
1.3 全等三角形的判定
第1课时 “边角边”
夹角 SAS
1. C 2. C 3. ①④ 4. 6
5. ∵ E是AC的中点,∴ AE=CE.在△ADE和△CFE中,∴ △ADE≌△CFE(SAS),∴ ∠ADE=∠CFE,∴ CF∥AB
第2课时 “角边角”
夹边 ASA
1. C 2. D 3. 角边角(或ASA) 4. 54°
5. ∵ AE平分∠BAD,∴ ∠BAC=∠DAC.∵ ∠BCE+∠ACB=180°,∠DCE+∠ACD=180°,∠BCE=∠DCE,∴ ∠ACB=∠ACD.在△ACB和△ACD中,∴ △ACB≌△ACD(ASA),∴ AB=AD
第3课时 “角角边”
对边 AAS
1. C 2. C 3. 答案不唯一,如∠ABO=∠CDO 4. 1
5. (1) ∵ AC⊥BC,AD⊥BD,∴ ∠C=∠D=90°.在△ABC和△BAD中,∴ △ABC≌△BAD(AAS) (2) ∵ △ADB的内角和为180°,∠DAB=70°,∠D=90°,∴ ∠DBA=90°-70°=20°.∵ △ABC≌△BAD,∴ ∠CAB=∠DBA=20°
第4课时 “边边边”
1. 相等 SSS 2. 稳定
1. D 2. B 3. AB∥DE,BC∥EF 4. 70 5. 60°
6. ∵ C是BD的中点,∴ BC=DC.在△ABC和△EDC中,∴ △ABC≌△EDC(SSS),∴ ∠ACB=∠ECD,∴ ∠ACB+∠ACE=∠ECD+∠ACE,即∠ECB=∠ACD
第5课时 灵活运用“SAS、ASA、AAS、SSS”判定两个三角形全等
SAS ASA AAS SSS
1. D 2. B 3. 答案不唯一,如DE=EF 4. 3 5. ∠A=∠C ∠AEB=∠CDB BE=BD 6. EBD
EB 27. ∵ △ABC≌△A'B'C',∴ ∠B=∠B',AB=A'B',∠BAC=∠B'A'C'.∵ AD,A'D'分别是△ABC与△A'B'C'的角平分线,∴ ∠BAD=∠BAC,∠B'A'D'=∠B'A'C',∴ ∠BAD=∠B'A'D'.在△ABD和△A'B'D'中,∴ △ABD≌△A'B'D'(ASA),∴ AD=A'D'
8. 在△ABF和△ACE中,∴ △ABF≌△ACE(SAS),∴ ∠ABF=∠ACE.∵ AB=AC,AE=AF,∴ AB-AE=AC-AF,即BE=CF.在△BEP和△CFP中,∴ △BEP≌△CFP(AAS),∴ PB=PC 题图中其他相等的线段为PE和PF,BE和CF,BF和CE
9. (1) 如图,连接BC.在△ABC和△DCB中,∴ △ABC≌△DCB(SSS),∴ ∠A=∠D (2) 在△ABO和△DCO中,∴ △ABO≌△DCO(AAS),∴ AO=DO
第6课时 直角三角形全等的判定
1. Rt△ 2. 一条直角边 HL
1. D 2. C 3. 10 4. 55°
5. ∵ ∠ADC=∠AEB=90°,∴ ∠BDO=∠CEO=90°.在△DOB和△EOC中,∴ △DOB≌△EOC(AAS),∴ OD=OE.在Rt△ADO和Rt△AEO中,∴ Rt△ADO≌Rt△AEO(HL),∴ ∠1=∠2
第1课时 “边角边”
两边及其 分别相等的两个三角形全等(简写成“边角边”或“ ”).
1. (教材P17例2变式)如图,在△ABD和△ACE中,AB=AC,AD=AE.若要用“SAS”判定△ABD≌△ACE,则可补充的条件是 ( )
A. ∠B=∠C B. ∠D=∠E C. ∠BAD=∠CAE D. ∠B=∠E
2.
(2023·福建改编)如图,AB=AC,AD=AE,∠BAC=∠DAE,则下列结论错误的是 ( )
A. ∠BAD=∠CAE B. △ABD≌△ACE
C. AB=BC D. BD=CE
3. 如图,有下列条件:① BC=AD,∠ABC=∠BAD;② BC=AD,AC=BD;③ BC=AD,∠CAB=∠DBA;④ AC=BD,∠BAC=∠ABD.其中,能用“SAS”判定△ABC≌△BAD的是 (填序号).
4. 如图,点B,E,C,F在同一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF的长为 .
5. (2024·南通)如图,点D在△ABC的边AB上,DF经过边AC的中点E,且EF=DE.
求证:CF∥AB.
第5题
第2课时 “角边角”
两角及其 分别相等的两个三角形全等(简写成“角边角”或“ ”).
1.
如图,∠A=∠D,∠1=∠2.若要用“ASA”判定△ABC≌△DEF,还应给出的条件是 ( )
A. ∠E=∠B B. ED=BC C. AF=CD D. AB=EF
2. 如图,D是△ABC的边AB上的一点,DF交AC于点E,DE=EF,FC∥AB.若BD=2,CF=5,则AB的长为 ( )
A. 1 B. 3 C. 5 D. 7
3. (新情境·现实生活)如图,某三角形材料断裂成Ⅰ,Ⅱ,Ⅲ三块,现要配置与原材料全等的三角形材料,应该利用材料Ⅲ,这样做利用的是三角形全等的判定方法中的“ ”.
4. 如图,当∠α的度数为 时,图中的两个三角形全等.
5. 如图,AE平分∠BAD,∠BCE=∠DCE.求证:AB=AD.
第5题
第3课时 “角角边”
基本事实“角边角”的推论:两角分别相等且其中一组等角的 相等的两个三角形全等(简写成“角角边”或“ ”).
1.
如图,在△ABC中,∠B=∠C,D为BC的中点,由点D分别向AB,AC作垂线段,垂足分别为E,F,则证明△BDE≌△CDF的依据是 ( )
A. SAS B. ASA C. AAS D. 以上均不对
2. (2023·衢州改编)如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列条件中的一个无法证明△ABC≌△DEF的是 ( )
A. AC∥DF B. ∠A=∠D C. AC=DF D. ∠ACB=∠F
3. 如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,添加一个条件: ,可利用“AAS”来判定△AOB≌△COD.
4. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于点H.若EH=EB=3,AE=4,则CH的长为 .
5. (2024·镇江)如图,AD⊥BD,AC⊥BC,∠CBA=∠DAB.
(1) 求证:△ABC≌△BAD;
(2) 若∠DAB=70°,求∠CAB的度数.
第5题
第4课时 “边边边”
1. 三边分别 的两个三角形全等(简写成“边边边”或“ ”).
2. 如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定,三角形的这个性质叫作三角形的 性.
1.
(新情境·现实生活)为了解决野外测绘时地面凹凸不平的问题,测绘仪支撑架均做成三条腿,这运用了三角形的 ( )
A. 旋转不变形 B. 平移不变形 C. 对称性 D. 稳定性
2. 如图,AB=AC,BD=CD,可推出 ( )
A. △BAD≌△BCD B. △ABD≌△ACD
C. △ACD≌△BCD D. △ACE≌△BDE
3. 如图,点A,D,C,F在同一条直线上,AB=DE,AD=CF,BC=EF,则图中互相平行的线段是 .
4. (2024·姑苏区期末)如图,AD=DE,AB=BE,∠CED=110°,则∠A= °.
5. 如图,AB=CD,AD=BC,∠1=40°,∠2=80°,则∠B的度数为 .
6. (2023·云南改编)如图,C是BD的中点,AB=ED,AC=EC.求证:∠ECB=∠ACD.
第6题
第5课时 灵活运用“SAS、ASA、AAS、SSS” 判定两个三角形全等
到目前为止,我们已经学过判定两个三角形全等的方法有 、 、 、 (简记).
1.
如图,下列各组条件中,能用“SAS”或“ASA”或“AAS”判定△ABC≌△DEF的是 ( )
A. AB=DE,AC=DF,∠C=∠F B. AB=DE,∠A=∠D,BC=EF
C. AC=DF,∠A=∠D,BC=EF D. AC=DF,∠C=∠F,BC=EF
2. 如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB,则下列结论正确的是 ( )
A. ∠A=∠C B. ∠A=∠E
C. AC=DE D. B是AD的中点
3. (2024·牡丹江)如图,在△ABC中,D是AB上一点,CF∥AB,D,E,F三点共线,请添加一个条件: ,使得AE=CE(写出一种即可).
4. 如图,AD是△ABC的角平分线.若∠B=90°,BD=3,则点D到AC的距离是 .
5. 如图,AB=CB,要说明△ABE≌△CBD.
如果直接利用“ASA”,那么要补充的条件是 ;
如果直接利用“AAS”,那么要补充的条件是 ;
如果直接利用“SAS”,那么要补充的条件是 .
6. 如图,在△ABC中,AB=5,AC=3,AD是△ABC的中线,设AD的长为m.延长AD到点E,使DE=AD,连接BE.由“SAS”可证得△ACD≌△ ,因此 =AC=3.在△ABE中,根据三角形三边的不等关系,可得AE长度的取值范围是 ,从而得到△ABC的中线AD长度的取值范围是 ,即m的取值范围是 .
7. (教材P22例4变式)如图,△ABC≌△A'B'C',AD,A'D'分别是△ABC与△A'B'C'的角平分线.求证:AD=A'D'.
8. 如图,在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.
第8题
9. 如图,AC,BD相交于点O,且AB=CD,AC=DB.求证:
(1) ∠A=∠D;
(2) AO=DO.
第9题
第6课时 直角三角形全等的判定
1. 直角三角形是特殊的三角形,可以用符号“ ”表示.
2. 斜边和 分别相等的两个直角三角形全等(简写成“ ”).
1.
判定两个直角三角形全等的条件可以是 ( )
A. 一锐角对应相等 B. 两锐角对应相等
C. 一条边对应相等 D. 两条边对应相等
2. 如图,在四边形ABCD中,AC与BD相交于点O,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F,连接CE,AF,则图中与AO长度相等的线段是 ( )
A. AD B. DO C. CO D. BO
3. 如图,AB⊥CD,且AB=CD,CE⊥AD,BF⊥AD,垂足分别为E,F,且满足CE=AF.若AE=4,BF=6,则AD的长为 .
4. 如图,在△ABC中,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF的度数为 .
5. (2023·南通)如图,点D,E分别在AB,AC上,∠ADC=∠AEB=90°,BE,CD相交于点O,OB=OC,连接AO.求证:∠1=∠2.
第5题
1.3 全等三角形的判定
第1课时 “边角边”
夹角 SAS
1. C 2. C 3. ①④ 4. 6
5. ∵ E是AC的中点,∴ AE=CE.在△ADE和△CFE中,∴ △ADE≌△CFE(SAS),∴ ∠ADE=∠CFE,∴ CF∥AB
第2课时 “角边角”
夹边 ASA
1. C 2. D 3. 角边角(或ASA) 4. 54°
5. ∵ AE平分∠BAD,∴ ∠BAC=∠DAC.∵ ∠BCE+∠ACB=180°,∠DCE+∠ACD=180°,∠BCE=∠DCE,∴ ∠ACB=∠ACD.在△ACB和△ACD中,∴ △ACB≌△ACD(ASA),∴ AB=AD
第3课时 “角角边”
对边 AAS
1. C 2. C 3. 答案不唯一,如∠ABO=∠CDO 4. 1
5. (1) ∵ AC⊥BC,AD⊥BD,∴ ∠C=∠D=90°.在△ABC和△BAD中,∴ △ABC≌△BAD(AAS) (2) ∵ △ADB的内角和为180°,∠DAB=70°,∠D=90°,∴ ∠DBA=90°-70°=20°.∵ △ABC≌△BAD,∴ ∠CAB=∠DBA=20°
第4课时 “边边边”
1. 相等 SSS 2. 稳定
1. D 2. B 3. AB∥DE,BC∥EF 4. 70 5. 60°
6. ∵ C是BD的中点,∴ BC=DC.在△ABC和△EDC中,∴ △ABC≌△EDC(SSS),∴ ∠ACB=∠ECD,∴ ∠ACB+∠ACE=∠ECD+∠ACE,即∠ECB=∠ACD
第5课时 灵活运用“SAS、ASA、AAS、SSS”判定两个三角形全等
SAS ASA AAS SSS
1. D 2. B 3. 答案不唯一,如DE=EF 4. 3 5. ∠A=∠C ∠AEB=∠CDB BE=BD 6. EBD
EB 2
8. 在△ABF和△ACE中,∴ △ABF≌△ACE(SAS),∴ ∠ABF=∠ACE.∵ AB=AC,AE=AF,∴ AB-AE=AC-AF,即BE=CF.在△BEP和△CFP中,∴ △BEP≌△CFP(AAS),∴ PB=PC 题图中其他相等的线段为PE和PF,BE和CF,BF和CE
9. (1) 如图,连接BC.在△ABC和△DCB中,∴ △ABC≌△DCB(SSS),∴ ∠A=∠D (2) 在△ABO和△DCO中,∴ △ABO≌△DCO(AAS),∴ AO=DO
第6课时 直角三角形全等的判定
1. Rt△ 2. 一条直角边 HL
1. D 2. C 3. 10 4. 55°
5. ∵ ∠ADC=∠AEB=90°,∴ ∠BDO=∠CEO=90°.在△DOB和△EOC中,∴ △DOB≌△EOC(AAS),∴ OD=OE.在Rt△ADO和Rt△AEO中,∴ Rt△ADO≌Rt△AEO(HL),∴ ∠1=∠2
同课章节目录
