1.5 等腰三角形 同步练 (4课时,含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 1.5 等腰三角形 同步练 (4课时,含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 22:08:51 | ||
图片预览

文档简介
1.5 等腰三角形
第1课时 等腰三角形及其性质
1. 有两条 相等的三角形叫作等腰三角形,相等的 叫作腰.
2. 等腰三角形的性质定理1:等腰三角形的 相等(简称“等边对等角”).
3. 等腰三角形的性质定理2:等腰三角形 、 及 重合(简称“三线合一”).
1.
下列阐述正确的是 ( )
A. 等腰三角形中至少有两个内角相等 B. 等腰三角形只能有两边相等
C. 等腰三角形不是轴对称图形 D. 等腰三角形底边上的高是它的对称轴
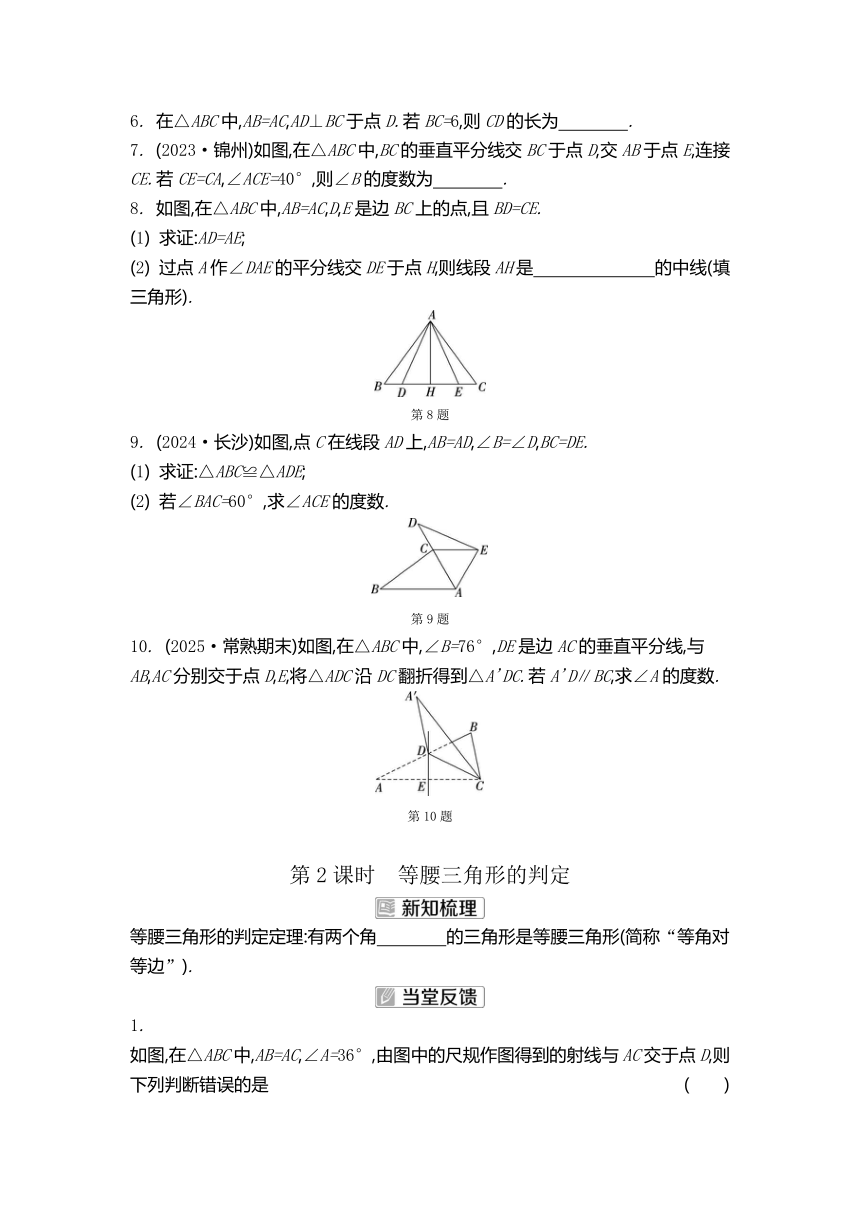
2. (2024·太仓期中)我国的桥梁建设在世界上处于领先地位,无论是桥梁数量、跨度还是技术创新,都取得了显著成就.如图为某斜拉索桥的示意图,该斜拉索桥的拉索和桥面构成等腰三角形,在△ABC中,AB=AC,若D是BC边上的一点,则下列条件不能说明AD⊥BC的是 ( )
A. BD=CD B. ∠ADB=∠ADC C. ∠BAD=∠CAD D. BC=2AD
3. 如图,∠AOB=40°,按下面的步骤作图:① 在边OA上取一点D,以点O为圆心,OD长为半径画弧,交OB于点C,连接CD;② 以点D为圆心,DO长为半径画弧,交OB于点E,连接DE,则∠CDE的度数为 ( )
A. 20° B. 30° C. 40° D. 50°
4. (2024·湖南)若等腰三角形的一个底角的度数为40°,则它的顶角的度数为 °.
5. (2024·兰州)如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB的度数为 .
6. 在△ABC中,AB=AC,AD⊥BC于点D.若BC=6,则CD的长为 .
7. (2023·锦州)如图,在△ABC中,BC的垂直平分线交BC于点D,交AB于点E,连接CE.若CE=CA,∠ACE=40°,则∠B的度数为 .
8. 如图,在△ABC中,AB=AC,D,E是边BC上的点,且BD=CE.
(1) 求证:AD=AE;
(2) 过点A作∠DAE的平分线交DE于点H,则线段AH是 的中线(填三角形).
第8题
9. (2024·长沙)如图,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
(1) 求证:△ABC≌△ADE;
(2) 若∠BAC=60°,求∠ACE的度数.
第9题
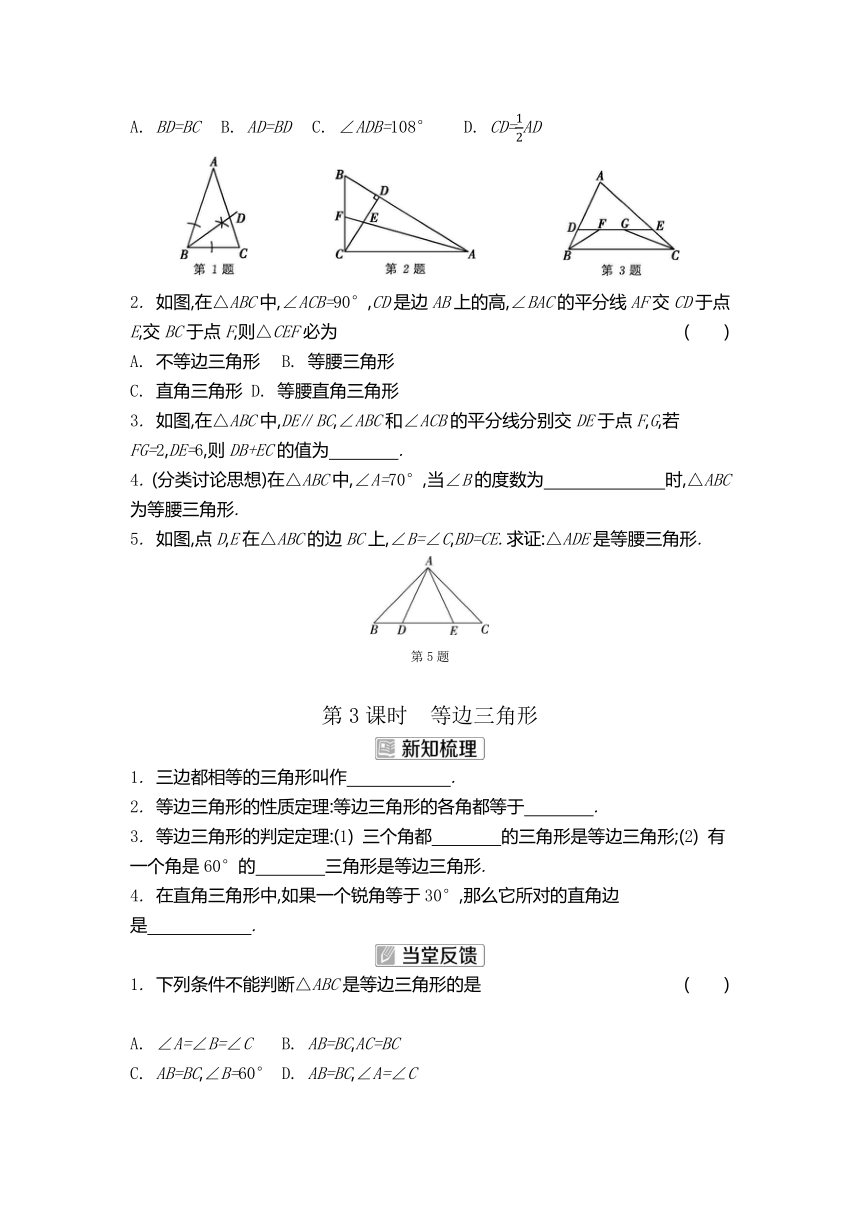
10. (2025·常熟期末)如图,在△ABC中,∠B=76°,DE是边AC的垂直平分线,与AB,AC分别交于点D,E,将△ADC沿DC翻折得到△A'DC.若A'D∥BC,求∠A的度数.
第10题
第2课时 等腰三角形的判定
等腰三角形的判定定理:有两个角 的三角形是等腰三角形(简称“等角对等边”).
1.
如图,在△ABC中,AB=AC,∠A=36°,由图中的尺规作图得到的射线与AC交于点D,则下列判断错误的是 ( )
A. BD=BC B. AD=BD C. ∠ADB=108° D. CD=AD
2. 如图,在△ABC中,∠ACB=90°,CD是边AB上的高,∠BAC的平分线AF交CD于点E,交BC于点F,则△CEF必为 ( )
A. 不等边三角形 B. 等腰三角形
C. 直角三角形 D. 等腰直角三角形
3. 如图,在△ABC中,DE∥BC,∠ABC和∠ACB的平分线分别交DE于点F,G,若FG=2,DE=6,则DB+EC的值为 .
4. (分类讨论思想)在△ABC中,∠A=70°,当∠B的度数为 时,△ABC为等腰三角形.
5. 如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE.求证:△ADE是等腰三角形.
第5题
第3课时 等边三角形
1. 三边都相等的三角形叫作 .
2. 等边三角形的性质定理:等边三角形的各角都等于 .
3. 等边三角形的判定定理:(1) 三个角都 的三角形是等边三角形;(2) 有一个角是60°的 三角形是等边三角形.
4. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边是 .
1. 下列条件不能判断△ABC是等边三角形的是 ( )
A. ∠A=∠B=∠C B. AB=BC,AC=BC
C. AB=BC,∠B=60° D. AB=BC,∠A=∠C
2. 在Rt△ABC中,∠A=90°,若∠C=2∠B,AC=5,则BC的长为 .
3. (2023·绵阳改编)如图,在等边三角形ABC中,BD是边AC上的中线,延长BC至点E,使CE=CD,则∠BDE的度数为 .
4. (2025·太仓期末)如图,l1∥l2,等边三角形ABC的顶点A在直线l1上,l2与△ABC的两边AC,BC相交.若∠1=138°,则∠2的度数为 .
5. 如图,在Rt△ABC中,∠ACB=90°,∠A=15°,AB的垂直平分线与AC交于点D,与AB交于点E,连接BD.若AD=12,则BC的长为 .
6. (2023·广西改编)如图,△ABC是边长为4的等边三角形,点D,E,F分别在边AB,BC,CA上运动,且满足AD=BE=CF.求证:△DEF为等边三角形.
第6题
第4课时 直角三角形的性质定理
直角三角形的性质定理:直角三角形斜边上的中线等于 的一半.
1. (2024·青海)如图,在Rt△ABC中,D是AC的中点,∠BDC=60°,AC=6,则BC的长是( )
A. 3 B. 6 C. 1.7 D. 5.2
2. (新情境·现实生活)如图,点A,B,C分别表示三个村庄,AB⊥BC.为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在 ( )
A. AB的中点处 B. BC的中点处
C. AC的中点处 D. ∠C的平分线与AB的交点处
3. 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.若∠B=50°,则∠ACD的度数为 .
4. 如图,在△ABC中,∠ABC=∠C,AD是角平分线,BE是中线.若DE=12,则AB的长为 .
5. 如图,在Rt△ACB中,∠ACB=90°,M为边AB的中点,点E在线段AM上,连接CM,CE,∠A=50°,∠ACE=30°.求证:CE=CM.
第5题
1.5 等腰三角形
第1课时 等腰三角形及其性质
1. 边 边 2. 两底角 3. 底边上的高线 中线 顶角平分线
1. A 2. D 3. B 4. 100 5. 115° 6. 3 7. 35°
8. (1) ∵ AB=AC,∴ ∠B=∠C.在△ABD和△ACE中,∴ △ABD≌△ACE(SAS),∴ AD=AE
(2) △ABC,△ADE
9. (1) 在△ABC和△ADE中,∴ △ABC≌△ADE(SAS) (2) ∵ △ABC≌△ADE,∴ AC=AE,∠BAC=∠DAE=60°,∴ ∠AEC=∠ACE.∵ △ACE的内角和为180°,∴ ∠ACE=(180°-∠DAE)=60°
10. ∵ ∠B=76°,A'D∥BC,∴ ∠A'DB=∠B=76°.设∠BDC=α,则∠A'DC=76°+α.∵ DC是折痕,∴ ∠ADC=∠A'DC=76°+α.∵ ∠ADC+∠BDC=180°,∴ 76°+α+α=180°,解得α=52°,∴ ∠BDC=52°.∵ DE是边AC的垂直平分线,∴ AD=CD,∴ ∠A=∠DCA.∵ ∠BDC=∠A+∠DCA,∴ ∠A=∠BDC=26°
第2课时 等腰三角形的判定
相等
1. D 2. B 3. 4 4. 55°或70°或40°
5. ∵ ∠B=∠C,∴ AB=AC.在△ABD和△ACE中,∴ △ABD≌△ACE,∴ AD=AE,∴ △ADE是等腰三角形
第3课时 等边三角形
1. 等边三角形 2. 60° 3. (1) 相等 (2) 等腰 4. 斜边的一半
1. D 2. 10 3. 120° 4. 102° 5. 6
6. ∵ △ABC是等边三角形,∴ ∠A=∠B=60°,AB=AC.∵ AD=CF,∴ AC-CF=AB-AD,即AF=BD.在△ADF和△BED中,∴ △ADF≌△BED(SAS),∴ DF=ED.同理,可得DF=FE,∴ DF=ED=FE,∴ △DEF为等边三角形
第4课时 直角三角形的性质定理
斜边
1. A 2. C 3. 40° 4. 24
5. ∵ ∠ACB=90°,M为边AB的中点,∴ MC=MB,∴ ∠MCB=∠B.∵ ∠A=50°,∴ ∠MCB=∠B=40°,∴ ∠EMC=∠MCB+∠B=80°.∵ ∠ACE=30°,∴ ∠MEC=∠A+∠ACE=80°,∴ ∠MEC=∠EMC,∴ CE=CM
第1课时 等腰三角形及其性质
1. 有两条 相等的三角形叫作等腰三角形,相等的 叫作腰.
2. 等腰三角形的性质定理1:等腰三角形的 相等(简称“等边对等角”).
3. 等腰三角形的性质定理2:等腰三角形 、 及 重合(简称“三线合一”).
1.
下列阐述正确的是 ( )
A. 等腰三角形中至少有两个内角相等 B. 等腰三角形只能有两边相等
C. 等腰三角形不是轴对称图形 D. 等腰三角形底边上的高是它的对称轴
2. (2024·太仓期中)我国的桥梁建设在世界上处于领先地位,无论是桥梁数量、跨度还是技术创新,都取得了显著成就.如图为某斜拉索桥的示意图,该斜拉索桥的拉索和桥面构成等腰三角形,在△ABC中,AB=AC,若D是BC边上的一点,则下列条件不能说明AD⊥BC的是 ( )
A. BD=CD B. ∠ADB=∠ADC C. ∠BAD=∠CAD D. BC=2AD
3. 如图,∠AOB=40°,按下面的步骤作图:① 在边OA上取一点D,以点O为圆心,OD长为半径画弧,交OB于点C,连接CD;② 以点D为圆心,DO长为半径画弧,交OB于点E,连接DE,则∠CDE的度数为 ( )
A. 20° B. 30° C. 40° D. 50°
4. (2024·湖南)若等腰三角形的一个底角的度数为40°,则它的顶角的度数为 °.
5. (2024·兰州)如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB的度数为 .
6. 在△ABC中,AB=AC,AD⊥BC于点D.若BC=6,则CD的长为 .
7. (2023·锦州)如图,在△ABC中,BC的垂直平分线交BC于点D,交AB于点E,连接CE.若CE=CA,∠ACE=40°,则∠B的度数为 .
8. 如图,在△ABC中,AB=AC,D,E是边BC上的点,且BD=CE.
(1) 求证:AD=AE;
(2) 过点A作∠DAE的平分线交DE于点H,则线段AH是 的中线(填三角形).
第8题
9. (2024·长沙)如图,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
(1) 求证:△ABC≌△ADE;
(2) 若∠BAC=60°,求∠ACE的度数.
第9题
10. (2025·常熟期末)如图,在△ABC中,∠B=76°,DE是边AC的垂直平分线,与AB,AC分别交于点D,E,将△ADC沿DC翻折得到△A'DC.若A'D∥BC,求∠A的度数.
第10题
第2课时 等腰三角形的判定
等腰三角形的判定定理:有两个角 的三角形是等腰三角形(简称“等角对等边”).
1.
如图,在△ABC中,AB=AC,∠A=36°,由图中的尺规作图得到的射线与AC交于点D,则下列判断错误的是 ( )
A. BD=BC B. AD=BD C. ∠ADB=108° D. CD=AD
2. 如图,在△ABC中,∠ACB=90°,CD是边AB上的高,∠BAC的平分线AF交CD于点E,交BC于点F,则△CEF必为 ( )
A. 不等边三角形 B. 等腰三角形
C. 直角三角形 D. 等腰直角三角形
3. 如图,在△ABC中,DE∥BC,∠ABC和∠ACB的平分线分别交DE于点F,G,若FG=2,DE=6,则DB+EC的值为 .
4. (分类讨论思想)在△ABC中,∠A=70°,当∠B的度数为 时,△ABC为等腰三角形.
5. 如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE.求证:△ADE是等腰三角形.
第5题
第3课时 等边三角形
1. 三边都相等的三角形叫作 .
2. 等边三角形的性质定理:等边三角形的各角都等于 .
3. 等边三角形的判定定理:(1) 三个角都 的三角形是等边三角形;(2) 有一个角是60°的 三角形是等边三角形.
4. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边是 .
1. 下列条件不能判断△ABC是等边三角形的是 ( )
A. ∠A=∠B=∠C B. AB=BC,AC=BC
C. AB=BC,∠B=60° D. AB=BC,∠A=∠C
2. 在Rt△ABC中,∠A=90°,若∠C=2∠B,AC=5,则BC的长为 .
3. (2023·绵阳改编)如图,在等边三角形ABC中,BD是边AC上的中线,延长BC至点E,使CE=CD,则∠BDE的度数为 .
4. (2025·太仓期末)如图,l1∥l2,等边三角形ABC的顶点A在直线l1上,l2与△ABC的两边AC,BC相交.若∠1=138°,则∠2的度数为 .
5. 如图,在Rt△ABC中,∠ACB=90°,∠A=15°,AB的垂直平分线与AC交于点D,与AB交于点E,连接BD.若AD=12,则BC的长为 .
6. (2023·广西改编)如图,△ABC是边长为4的等边三角形,点D,E,F分别在边AB,BC,CA上运动,且满足AD=BE=CF.求证:△DEF为等边三角形.
第6题
第4课时 直角三角形的性质定理
直角三角形的性质定理:直角三角形斜边上的中线等于 的一半.
1. (2024·青海)如图,在Rt△ABC中,D是AC的中点,∠BDC=60°,AC=6,则BC的长是( )
A. 3 B. 6 C. 1.7 D. 5.2
2. (新情境·现实生活)如图,点A,B,C分别表示三个村庄,AB⊥BC.为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在 ( )
A. AB的中点处 B. BC的中点处
C. AC的中点处 D. ∠C的平分线与AB的交点处
3. 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.若∠B=50°,则∠ACD的度数为 .
4. 如图,在△ABC中,∠ABC=∠C,AD是角平分线,BE是中线.若DE=12,则AB的长为 .
5. 如图,在Rt△ACB中,∠ACB=90°,M为边AB的中点,点E在线段AM上,连接CM,CE,∠A=50°,∠ACE=30°.求证:CE=CM.
第5题
1.5 等腰三角形
第1课时 等腰三角形及其性质
1. 边 边 2. 两底角 3. 底边上的高线 中线 顶角平分线
1. A 2. D 3. B 4. 100 5. 115° 6. 3 7. 35°
8. (1) ∵ AB=AC,∴ ∠B=∠C.在△ABD和△ACE中,∴ △ABD≌△ACE(SAS),∴ AD=AE
(2) △ABC,△ADE
9. (1) 在△ABC和△ADE中,∴ △ABC≌△ADE(SAS) (2) ∵ △ABC≌△ADE,∴ AC=AE,∠BAC=∠DAE=60°,∴ ∠AEC=∠ACE.∵ △ACE的内角和为180°,∴ ∠ACE=(180°-∠DAE)=60°
10. ∵ ∠B=76°,A'D∥BC,∴ ∠A'DB=∠B=76°.设∠BDC=α,则∠A'DC=76°+α.∵ DC是折痕,∴ ∠ADC=∠A'DC=76°+α.∵ ∠ADC+∠BDC=180°,∴ 76°+α+α=180°,解得α=52°,∴ ∠BDC=52°.∵ DE是边AC的垂直平分线,∴ AD=CD,∴ ∠A=∠DCA.∵ ∠BDC=∠A+∠DCA,∴ ∠A=∠BDC=26°
第2课时 等腰三角形的判定
相等
1. D 2. B 3. 4 4. 55°或70°或40°
5. ∵ ∠B=∠C,∴ AB=AC.在△ABD和△ACE中,∴ △ABD≌△ACE,∴ AD=AE,∴ △ADE是等腰三角形
第3课时 等边三角形
1. 等边三角形 2. 60° 3. (1) 相等 (2) 等腰 4. 斜边的一半
1. D 2. 10 3. 120° 4. 102° 5. 6
6. ∵ △ABC是等边三角形,∴ ∠A=∠B=60°,AB=AC.∵ AD=CF,∴ AC-CF=AB-AD,即AF=BD.在△ADF和△BED中,∴ △ADF≌△BED(SAS),∴ DF=ED.同理,可得DF=FE,∴ DF=ED=FE,∴ △DEF为等边三角形
第4课时 直角三角形的性质定理
斜边
1. A 2. C 3. 40° 4. 24
5. ∵ ∠ACB=90°,M为边AB的中点,∴ MC=MB,∴ ∠MCB=∠B.∵ ∠A=50°,∴ ∠MCB=∠B=40°,∴ ∠EMC=∠MCB+∠B=80°.∵ ∠ACE=30°,∴ ∠MEC=∠A+∠ACE=80°,∴ ∠MEC=∠EMC,∴ CE=CM
同课章节目录
