2024新人教版八年级上数学 14.3 角的平分线 第2课时 角的平分线的判定 课件(共32张PPT)
文档属性
| 名称 | 2024新人教版八年级上数学 14.3 角的平分线 第2课时 角的平分线的判定 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
人教版(2024)
八年级上册
14.3 角的平分线
第2课时 角的平分线的判定
第十四章 · 全等三角形
角的平分线的判定
知识目标
1.明确“角的内部到角两边距离相等的点一定在该角的平分线上”,能准确表述其几何意义及符号语言。
2.通过逆向思维关联已学的“性质定理”,对比两者的区别与联系,形成完整的知识闭环。
能力目标
1.经历从直观感知到严谨证明的过程,学会用全等三角形完成逻辑推导,培养步骤规范性。
2.体会原命题与逆命题的关系,强化数学意识,提升分析问题时双向思考的习惯。
素质目标
1.在猜想—验证—修正的过程中渗透实证精神,拒绝主观臆断;通过多角度证明培养批判性思维。
2.鼓励尝试非常规解法,突破定式思维局限,体验数学的统一美。
教学难点
教学重点
解析“距离”的定义,强调“内部”“两边”“相等”三个关键词
判断一个点是否在一个角的平分线上
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:角的平分线的性质
角平分线上的点到角两边的距离相等.
A
O
B
P
C
D
E
应用定理需具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
生活中常见的轴对称图形
剪纸 木雕
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
生活中常见的轴对称图形
古建筑飞檐
这些图案为何如此和谐美观?背后是否有数学规律?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
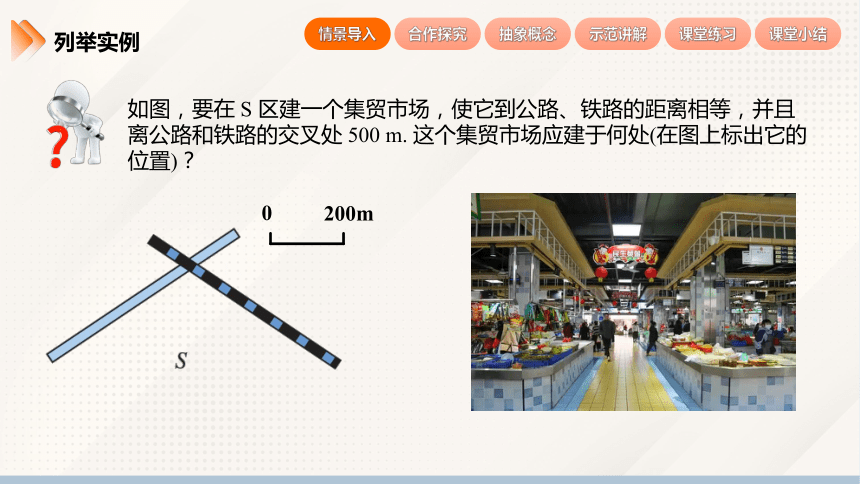
列举实例
如图,要在 S 区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路和铁路的交叉处 500 m. 这个集贸市场应建于何处(在图上标出它的位置)?
0
200m
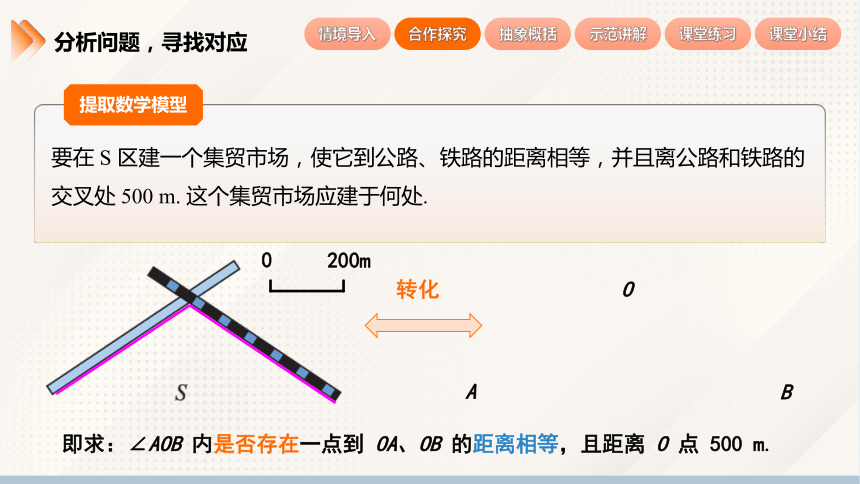
分析问题,寻找对应
要在 S 区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路和铁路的交叉处 500 m. 这个集贸市场应建于何处.
提取数学模型
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
即求:∠AOB 内是否存在一点到 OA、OB 的距离相等,且距离 O 点 500 m.
转化
A
O
B
0
200m
分析问题,寻找对应
交换“角的平分线上的点到角两边的距离相等” 这个性质的已知和结论,得到的命题还成立吗?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
角的内部到角的两边的距离相等的点在角的平分线上.
A
O
B
P
C
D
E
∵PD⊥OA,PE⊥OB, PD = PE,
∴点 P 在∠AOB的平分线上(OC 平分 ∠AOB).
你能证明这个结论是否成立吗?
分析问题,寻找对应
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE. 求证:点P在∠AOB的平分线上.
猜想证明
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
O
B
P
D
E
证明:
作射线OP,
∴点P在∠AOB的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知 ),
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
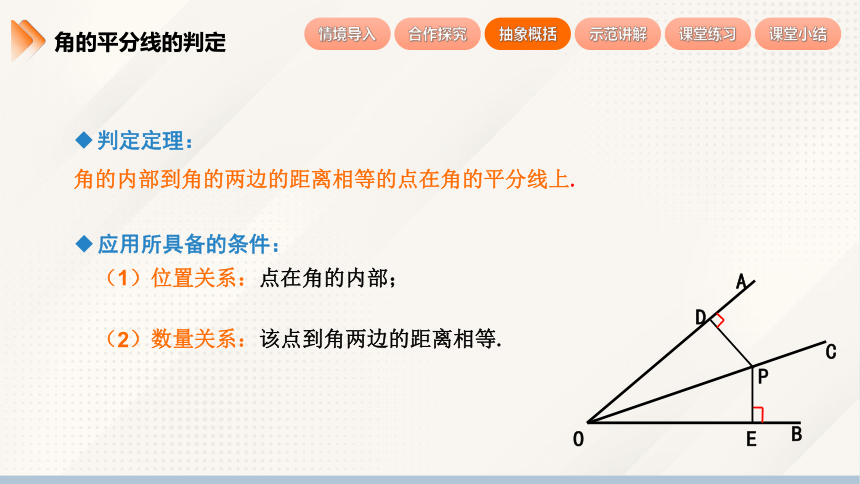
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
A
O
B
P
C
D
E
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
O
B
P
C
D
E
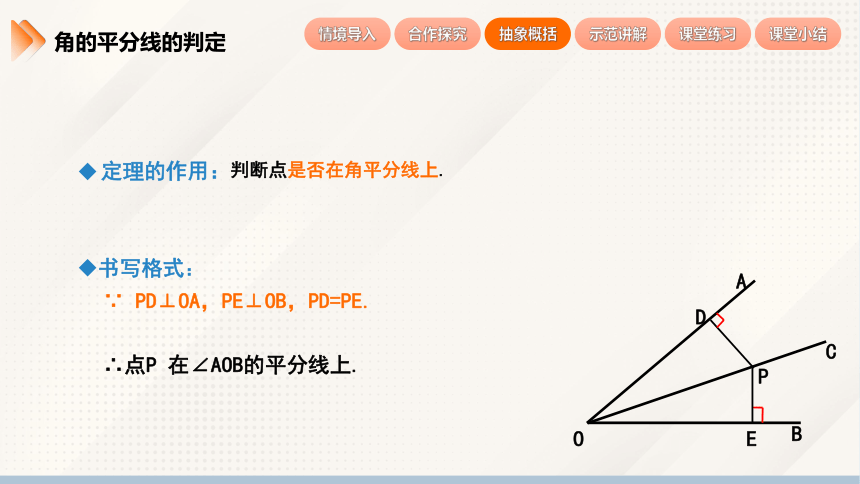
定理的作用:判断点是否在角平分线上.
书写格式:
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P 在∠AOB的平分线上.
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
数学思想:
角相等
角平分线的性质定理和它的逆定理,揭示了“角相等”和“线段相等”之间的一种特殊关系.
角平分线性质
角平分线性质定理的逆定理
线段相等
这为今后我们证明角相等,线段相等提供了一种解题思路.
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
数学思想:
角的平分线(顶点除外)可以看成到角两边距离相等的所有点的集合.
所有到角两边距离相等的点组成这个角的平分线
A
B
O
D1
E1
P1
D2
E2
P2
D3
E3
P3
D4
E4
P4
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
三角形的内角平分线
分别画出下列三角形三个内角的平分线,是否都相交于一点?
三角形的三条角平分线相交于一点.
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
三角形的内角平分线
分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
你能证明这个结论吗?
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
例1
A
B
C
P
N
M
D
E
F
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
这说明三角形的三条角平分线相交于一点,这一点到三角形三边的距离相等.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(1)求点O到△ABC三边的距离和.
例2
M
E
N
A
B
C
P
O
D
B
C
A
P
解:过点O作ON⊥BC , OE⊥AB,垂足分别为点N,点E .
∵两条角平分线相交于O
∴O到三边的距离相等
即 ON = OE = OM = 4
由题意得, ON + OE + OM =12.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(2)若△ABC的周长为32,求△ABC的面积.
例2
M
E
N
A
B
C
P
O
D
B
C
A
P
解:连接OC.
∵ON = OE = OM = 4,△ABC的周长为32
∴S△ABC=S△AOC+S△BOC+S△AOB
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
归纳总结
1.应用角平分线性质:
存在角平分线
涉及距离问题
2.联系角平分线性质:
距离
面积
周长
条件
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
E
∵点F在∠BCE的平分线上,FG⊥AE, FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
D
3.如图,已知∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
问:到三角形三边所在直线距离相等的点一共有几个?
解:4个
P1
P4
P2
P3
三角形三个内角的平分线的交点 P1;
三角形一个内角与另外两个角的外角的平分线的交点 P2,P3,P4.
4.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处 画出它的位置.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
5.如图,已知△ABC ,BF 是△ABC的外角∠CBD 的平分线,CG 是△ABC 的外角∠BCE 的平分线,BF,CG 相交于点 P. 求证:
(1)点 P 到三边 AB,BC,CA 所在直线的距离相等;
(2)点 P 在∠A 的平分线上.
C
A
B
D
E
F
G
P
J
I
H
证明:(1) 如图,过点 P 分别作 PJ,PI,PH 垂直于三边 AB,BC,AC 所在的直线,垂足分别为 J,I,H.
∵BF 是∠CBD 的平分线,点 P 在 BF 上,
∴PI = PJ.
同理,PH = PI,
∴PJ = PI = PH,
即点 P 到三边 AB,BC,CA 所在直线的距离相等.
(2)由(1)知 PH⊥AE,PJ⊥AD,且 PH = PJ,得点 P 在∠A 的平分线上.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
6.如图,AB⊥CD,CE⊥AD,垂足分别为 B,E,AB = CE,AB,CE 相交于点 F,连接 DF. 求证:FD 平分∠BFE.
C
A
B
D
E
F
证明:∵AB⊥CD,CE⊥AD,∴∠ABD =∠CED = 90°.
在△ABD 和△CED 中,
∠ADB =∠CDE,
∠ABD =∠CED,
AB = CE,
∴△ABD ≌△CED(AAS)
∴BD = ED.
又 AB⊥CD,CE⊥AD,
∴FD 平分∠BFE.
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(2021·青海·中考真题)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.8 C.15 D.无法确定
[答案]A
[详解]试题分析:如图,过点D作DE⊥BC于点E.
∵∠A=90°
∴AD⊥AB
∵BD平分∠ABC
∴AD=DE=3.
又∵BC=5, ∴S△BCD=BC·DE=x5x3=7.5.故选A.
E
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
理解角平分线的判定定理
通过逆向思维关联已学的“角的平分线性质定理”
判断点是否在角平分线上
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
角平分线
的判定定理
内容
角的内部到角两边距离相等的点在这个角的平分线上
作用
判断一个点是否在角的平分线上
结论
三角形的角平分线相交于内部一点
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.应用角平分线性质:
存在角平分线
涉及距离问题
2.联系角平分线性质:
距离
面积
周长
条件
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P52:习题14.3:2题.
B层:P52:习题14.3:8题.
下 课
人教版(2024)
八年级上册
14.3 角的平分线
第2课时 角的平分线的判定
第十四章 · 全等三角形
角的平分线的判定
知识目标
1.明确“角的内部到角两边距离相等的点一定在该角的平分线上”,能准确表述其几何意义及符号语言。
2.通过逆向思维关联已学的“性质定理”,对比两者的区别与联系,形成完整的知识闭环。
能力目标
1.经历从直观感知到严谨证明的过程,学会用全等三角形完成逻辑推导,培养步骤规范性。
2.体会原命题与逆命题的关系,强化数学意识,提升分析问题时双向思考的习惯。
素质目标
1.在猜想—验证—修正的过程中渗透实证精神,拒绝主观臆断;通过多角度证明培养批判性思维。
2.鼓励尝试非常规解法,突破定式思维局限,体验数学的统一美。
教学难点
教学重点
解析“距离”的定义,强调“内部”“两边”“相等”三个关键词
判断一个点是否在一个角的平分线上
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:角的平分线的性质
角平分线上的点到角两边的距离相等.
A
O
B
P
C
D
E
应用定理需具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
生活中常见的轴对称图形
剪纸 木雕
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
生活中常见的轴对称图形
古建筑飞檐
这些图案为何如此和谐美观?背后是否有数学规律?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例
如图,要在 S 区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路和铁路的交叉处 500 m. 这个集贸市场应建于何处(在图上标出它的位置)?
0
200m
分析问题,寻找对应
要在 S 区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路和铁路的交叉处 500 m. 这个集贸市场应建于何处.
提取数学模型
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
即求:∠AOB 内是否存在一点到 OA、OB 的距离相等,且距离 O 点 500 m.
转化
A
O
B
0
200m
分析问题,寻找对应
交换“角的平分线上的点到角两边的距离相等” 这个性质的已知和结论,得到的命题还成立吗?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
角的内部到角的两边的距离相等的点在角的平分线上.
A
O
B
P
C
D
E
∵PD⊥OA,PE⊥OB, PD = PE,
∴点 P 在∠AOB的平分线上(OC 平分 ∠AOB).
你能证明这个结论是否成立吗?
分析问题,寻找对应
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE. 求证:点P在∠AOB的平分线上.
猜想证明
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
O
B
P
D
E
证明:
作射线OP,
∴点P在∠AOB的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知 ),
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
A
O
B
P
C
D
E
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
O
B
P
C
D
E
定理的作用:判断点是否在角平分线上.
书写格式:
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P 在∠AOB的平分线上.
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
数学思想:
角相等
角平分线的性质定理和它的逆定理,揭示了“角相等”和“线段相等”之间的一种特殊关系.
角平分线性质
角平分线性质定理的逆定理
线段相等
这为今后我们证明角相等,线段相等提供了一种解题思路.
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
数学思想:
角的平分线(顶点除外)可以看成到角两边距离相等的所有点的集合.
所有到角两边距离相等的点组成这个角的平分线
A
B
O
D1
E1
P1
D2
E2
P2
D3
E3
P3
D4
E4
P4
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
三角形的内角平分线
分别画出下列三角形三个内角的平分线,是否都相交于一点?
三角形的三条角平分线相交于一点.
角的平分线的判定
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
三角形的内角平分线
分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
你能证明这个结论吗?
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
例1
A
B
C
P
N
M
D
E
F
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
这说明三角形的三条角平分线相交于一点,这一点到三角形三边的距离相等.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(1)求点O到△ABC三边的距离和.
例2
M
E
N
A
B
C
P
O
D
B
C
A
P
解:过点O作ON⊥BC , OE⊥AB,垂足分别为点N,点E .
∵两条角平分线相交于O
∴O到三边的距离相等
即 ON = OE = OM = 4
由题意得, ON + OE + OM =12.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,在直角△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP,BD交于点O,过点O作OM⊥AC,若OM=4.
(2)若△ABC的周长为32,求△ABC的面积.
例2
M
E
N
A
B
C
P
O
D
B
C
A
P
解:连接OC.
∵ON = OE = OM = 4,△ABC的周长为32
∴S△ABC=S△AOC+S△BOC+S△AOB
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
归纳总结
1.应用角平分线性质:
存在角平分线
涉及距离问题
2.联系角平分线性质:
距离
面积
周长
条件
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
E
∵点F在∠BCE的平分线上,FG⊥AE, FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
D
3.如图,已知∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
问:到三角形三边所在直线距离相等的点一共有几个?
解:4个
P1
P4
P2
P3
三角形三个内角的平分线的交点 P1;
三角形一个内角与另外两个角的外角的平分线的交点 P2,P3,P4.
4.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处 画出它的位置.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
5.如图,已知△ABC ,BF 是△ABC的外角∠CBD 的平分线,CG 是△ABC 的外角∠BCE 的平分线,BF,CG 相交于点 P. 求证:
(1)点 P 到三边 AB,BC,CA 所在直线的距离相等;
(2)点 P 在∠A 的平分线上.
C
A
B
D
E
F
G
P
J
I
H
证明:(1) 如图,过点 P 分别作 PJ,PI,PH 垂直于三边 AB,BC,AC 所在的直线,垂足分别为 J,I,H.
∵BF 是∠CBD 的平分线,点 P 在 BF 上,
∴PI = PJ.
同理,PH = PI,
∴PJ = PI = PH,
即点 P 到三边 AB,BC,CA 所在直线的距离相等.
(2)由(1)知 PH⊥AE,PJ⊥AD,且 PH = PJ,得点 P 在∠A 的平分线上.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
6.如图,AB⊥CD,CE⊥AD,垂足分别为 B,E,AB = CE,AB,CE 相交于点 F,连接 DF. 求证:FD 平分∠BFE.
C
A
B
D
E
F
证明:∵AB⊥CD,CE⊥AD,∴∠ABD =∠CED = 90°.
在△ABD 和△CED 中,
∠ADB =∠CDE,
∠ABD =∠CED,
AB = CE,
∴△ABD ≌△CED(AAS)
∴BD = ED.
又 AB⊥CD,CE⊥AD,
∴FD 平分∠BFE.
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(2021·青海·中考真题)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.8 C.15 D.无法确定
[答案]A
[详解]试题分析:如图,过点D作DE⊥BC于点E.
∵∠A=90°
∴AD⊥AB
∵BD平分∠ABC
∴AD=DE=3.
又∵BC=5, ∴S△BCD=BC·DE=x5x3=7.5.故选A.
E
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
理解角平分线的判定定理
通过逆向思维关联已学的“角的平分线性质定理”
判断点是否在角平分线上
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
角平分线
的判定定理
内容
角的内部到角两边距离相等的点在这个角的平分线上
作用
判断一个点是否在角的平分线上
结论
三角形的角平分线相交于内部一点
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.应用角平分线性质:
存在角平分线
涉及距离问题
2.联系角平分线性质:
距离
面积
周长
条件
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P52:习题14.3:2题.
B层:P52:习题14.3:8题.
下 课
同课章节目录
