2024-2025学年宁夏石嘴山三中高二(下)期中数学试卷(PDF版,含答案)
文档属性
| 名称 | 2024-2025学年宁夏石嘴山三中高二(下)期中数学试卷(PDF版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 97.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览



文档简介
2024-2025学年宁夏石嘴山三中高二(下)期中数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知命题p: n∈N,n2>2n,则命题p的否定是( )
A. n∈N,n2<2n B. n∈N,n2≤2n C. n∈N,n2≤2n D. n∈N,n2=2n
2.已知A={x|log2x≥-1},,则A∩B=( )
A. [1,2] B. (0,2] C. D.
3.探究学习小组收集了A早餐店2024年前六个月包子的售卖数据,得出每个月售卖包子的个数y(单位:万个)与月份x(x=1,2,3, ,6)的经验回归方程为,已知五月份的售卖量为2万个,则x=5时的残差为( )
A. -0.2 B. 0.2 C. -0.1 D. 0.1
4.函数f(x)=在(-∞,2)上的最小值是( )
A. 1 B. 2 C. 3 D. 0
5.蝗虫产卵量y与温度x的关系可用模型拟合,设z=lny,其变换后得到数据:
x 20 23 25 27 30
z 2 2.4 3 3 4.6
由上表可得经验回归方程,则c1=( )
A. e-2 B. e3 C. 2 D. 3
6.已知函数f(x+1)=x2+x,且函数f(x+1)的定义域为[-1,1],则( )
A. f(x)=x2+3x+1,x∈[-2,0] B. f(x)=x2+3x+1,x∈[0,2]
C. f(x)=x2-x,x∈[-2,0] D. f(x)=x2-x,x∈[0,2]
7.设a,b是关于x的一元二次方程x2-2mx+m+6=0的两个实根,则(a-1)2+(b-1)2的最小值是( )
A. B. 18 C. 8 D. -6
8.已知函数,若存在x2>x1>0,使得f(x2)=2f(x1),则x1 f(x2)的取值范围是( )
A. B.
C. (4,+∞) D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.下列命题为假命题的是( )
A. 若a>b,则ac2>bc2 B. 若a>b,则
C. 若a>b>0且c>0,则 D.
10.下列结论正确的是( )
A. 命题“若x=5,则x2-6x+5=0”为真命题
B. “x=5”是“x2-6x+5=0”的充分不必要条件
C. 已知命题p“若m>0,则方程x2+x-m=0有实数根”,则命题p的否定为真命题
D. 命题“若m2+n2=0,则m=0且n=0”为真命题
11.下列说法正确的是( )
A. 502019+1被7除后的余数为5
B. 两位男生和两位女生随机排成一列,则两位女生不相邻的概率是
C. 已知,则n=8
D. 从正方体的八个顶点中任取四个顶点,这四点能构成三棱锥的个数为58
三、填空题:本题共3小题,每小题5分,共15分。
12.若-1<a+b<1,2<a-b<3,t=3a+5b,则t的取值范围为______.
13.函数f(x)=ax2+ax+1,若对任意x∈R,f(x)>0恒成立,则实数a的取值范围是______.
14.现调查某地区某种野生动物的数量,将该地区分成面积相近的200个地块,从这些地块中简单随机抽样的方法抽取20个作为样本,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi、yi分别表示第i个样本的植物覆盖面积(单位:公顷)和这种野生动物的数量,构造向量,其中,,并计算得00,由选择性必修二教材中的知识,我们知道n对数据的相关系数,则上述数据(xi,yi)(i=1,2,…,20)的相关系数r= ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 1 2 3 4 5
工作年限x/年 3 5 6 7 9
(1)求年推销金额y关于工作年限x的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:回归直线的斜率和截距的最小二乘法估计公式分别为=,a=-b.
16.(本小题15分)
某校组织本校2000名学生进行针对性检测(检测分为初试和复试),并随机抽取了100名学生的初试成绩,绘制了频率分布直方图,如图所示.
(1)根据频率分布直方图,求样本平均数的估计值;(同一组数据用该区间的中点值作代表)
(2)若所有学生的初试成绩X近似服从正态分布N(μ,σ2),其中μ为样本平均数的估计值,σ≈14.初试成绩不低于90分的学生才能参加复试,试估计能参加复试的人数.(四舍五入精确到整数).
附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ≤X≤μ+σ)=0.6827,P(μ-2σ≤X≤μ+2σ)=0.9545,P(μ-3σ≤X≤μ+3σ)=0.9973.
17.(本小题15分)
某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按照题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(Ⅰ)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(Ⅱ)请分析比较甲、乙两人谁的面试通过的可能性大?
18.(本小题17分)
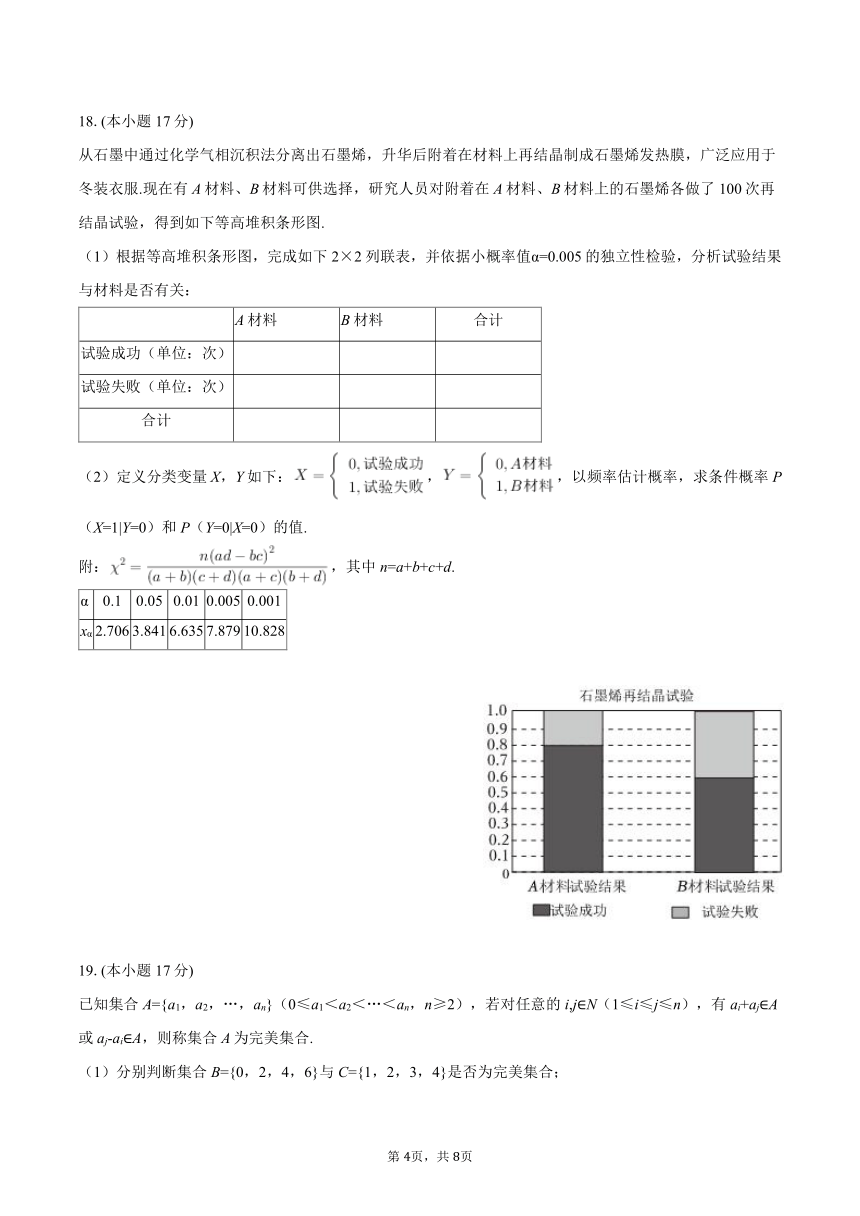
从石墨中通过化学气相沉积法分离出石墨烯,升华后附着在材料上再结晶制成石墨烯发热膜,广泛应用于冬装衣服.现在有A材料、B材料可供选择,研究人员对附着在A材料、B材料上的石墨烯各做了100次再结晶试验,得到如下等高堆积条形图.
(1)根据等高堆积条形图,完成如下2×2列联表,并依据小概率值α=0.005的独立性检验,分析试验结果与材料是否有关:
A材料 B材料 合计
试验成功(单位:次)
试验失败(单位:次)
合计
(2)定义分类变量X,Y如下:,,以频率估计概率,求条件概率P(X=1|Y=0)和P(Y=0|X=0)的值.
附:,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
19.(本小题17分)
已知集合A={a1,a2,…,an}(0≤a1<a2<…<an,n≥2),若对任意的i,j∈N(1≤i≤j≤n),有ai+aj∈A或aj-ai∈A,则称集合A为完美集合.
(1)分别判断集合B={0,2,4,6}与C={1,2,3,4}是否为完美集合;
(2)当n=3时,若a2=2,求完美集合A;
(3)若集合D={a1,a2,…,a2024}(0≤a1<a2<…<a2024)为完美集合,记,求证:S2024=1012(a1012+a1013).
1.【答案】C
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】D
9.【答案】AB
10.【答案】ABD
11.【答案】BCD
12.【答案】{t|-7<t<2}
13.【答案】[0,4)
14.【答案】
15.【答案】解:(1)设所求的线性回归方程为=x+,
=(3+5+6+7+9)=6,
=(2+3+3+4+5)=3.4,
∴==,
=0.4,
∴年销售金额y产于工作年限x的线性回归方程为=0.5x+0.4.
(2)当x=11时,=0.5x+0.4=0.5×11+0.4=5.9(万元),
∴可以估计第6名推销员的年推销金额为5.9万元.
16.【答案】62;
46.
17.【答案】解:(Ⅰ)设甲正确完成面试的题数为ξ,则ξ的取值分别为1,2,3.…(1分)
P(ξ=1)==;P(ξ=2)==;P(ξ=3)==; …(3分)
考生甲正确完成题数ξ的分布列为
ξ 1 2 3
P
Eξ=1×+2×+3×=2.…(4分)
设乙正确完成面试的题数为η,则η取值分别为0,1,2,3.…(5分)
P(η=0)=;P(η=1)==,P(η=2)==,P(η=3)==.…(7分)
考生乙正确完成题数η的分布列为:
η 0 1 2 3
P
Eη=0×+1×+2×+3×=2.…(8分)
(Ⅱ)因为Dξ==,…(10分)
Dη=npq=.…(12分)
所以Dξ<Dη.
综上所述,从做对题数的数学期望考查,两人水平相当;从做对题数的方差考查,甲较稳定;从至少完成2道题的概率考查,甲获得面试通过的可能性大.…(13分)
18.【答案】解:(1)由堆积等高条形图得2×2列联表为:
A材料 B材料 合计
试验成功(单位:次) 80 60 140
试验失败(单位:次) 20 40 60
合计 100 100 200
零假设:试验结果与材料无关,
==9.524>7,
依据小概率值α=0.005的独立检验,推断假设不成立,
即试验结果与材料有关,此推断犯错误的概率不超过0.005.
(2)依题意得:
n(Y=0)=100,n(X=1,Y=0)=20,
∴P(X=1|Y=0)===,
n(X=0)=140,n(Y=0,X=0)=80,
∴P(Y=0|X=0)===.
19.【答案】集合B={0,2,4,6}为完美集合,C={1,2,3,4}不是完美集合;
A={0,2,4};
证明:因为a2024+a2024=2a2024>a2024,故a2024+a2024 D,
所以a2024-a2024=0∈D,则a1=0.
因为ai<ai+1(i=1,2, ,2023),
所以a2024+a2023>a2024+a2022> >a2024+a2>a2024,
所以a2024+ai D(i=2,3, ,2023),
所以a2024-ai∈D(i=2,3, ,2023).
因为0<a2024-a2023<a2024-a2022< <a2024-a2<a2024,
所以a2024-a2023=a2,a2024-a2022=a3, ,a2024-a2=a2023,
又因为a2024-a2024=a1,a2024-a1=a2024,
全部相加得2024a2024-(a1+a2+ a2024)=a1+a2+ +a2024,即2S2024=2024a2024,
所以S2024=1012a2024,又a2024=a1012+a1013,所以S2024=1012(a1012+a1013).
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知命题p: n∈N,n2>2n,则命题p的否定是( )
A. n∈N,n2<2n B. n∈N,n2≤2n C. n∈N,n2≤2n D. n∈N,n2=2n
2.已知A={x|log2x≥-1},,则A∩B=( )
A. [1,2] B. (0,2] C. D.
3.探究学习小组收集了A早餐店2024年前六个月包子的售卖数据,得出每个月售卖包子的个数y(单位:万个)与月份x(x=1,2,3, ,6)的经验回归方程为,已知五月份的售卖量为2万个,则x=5时的残差为( )
A. -0.2 B. 0.2 C. -0.1 D. 0.1
4.函数f(x)=在(-∞,2)上的最小值是( )
A. 1 B. 2 C. 3 D. 0
5.蝗虫产卵量y与温度x的关系可用模型拟合,设z=lny,其变换后得到数据:
x 20 23 25 27 30
z 2 2.4 3 3 4.6
由上表可得经验回归方程,则c1=( )
A. e-2 B. e3 C. 2 D. 3
6.已知函数f(x+1)=x2+x,且函数f(x+1)的定义域为[-1,1],则( )
A. f(x)=x2+3x+1,x∈[-2,0] B. f(x)=x2+3x+1,x∈[0,2]
C. f(x)=x2-x,x∈[-2,0] D. f(x)=x2-x,x∈[0,2]
7.设a,b是关于x的一元二次方程x2-2mx+m+6=0的两个实根,则(a-1)2+(b-1)2的最小值是( )
A. B. 18 C. 8 D. -6
8.已知函数,若存在x2>x1>0,使得f(x2)=2f(x1),则x1 f(x2)的取值范围是( )
A. B.
C. (4,+∞) D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.下列命题为假命题的是( )
A. 若a>b,则ac2>bc2 B. 若a>b,则
C. 若a>b>0且c>0,则 D.
10.下列结论正确的是( )
A. 命题“若x=5,则x2-6x+5=0”为真命题
B. “x=5”是“x2-6x+5=0”的充分不必要条件
C. 已知命题p“若m>0,则方程x2+x-m=0有实数根”,则命题p的否定为真命题
D. 命题“若m2+n2=0,则m=0且n=0”为真命题
11.下列说法正确的是( )
A. 502019+1被7除后的余数为5
B. 两位男生和两位女生随机排成一列,则两位女生不相邻的概率是
C. 已知,则n=8
D. 从正方体的八个顶点中任取四个顶点,这四点能构成三棱锥的个数为58
三、填空题:本题共3小题,每小题5分,共15分。
12.若-1<a+b<1,2<a-b<3,t=3a+5b,则t的取值范围为______.
13.函数f(x)=ax2+ax+1,若对任意x∈R,f(x)>0恒成立,则实数a的取值范围是______.
14.现调查某地区某种野生动物的数量,将该地区分成面积相近的200个地块,从这些地块中简单随机抽样的方法抽取20个作为样本,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi、yi分别表示第i个样本的植物覆盖面积(单位:公顷)和这种野生动物的数量,构造向量,其中,,并计算得00,由选择性必修二教材中的知识,我们知道n对数据的相关系数,则上述数据(xi,yi)(i=1,2,…,20)的相关系数r= ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 1 2 3 4 5
工作年限x/年 3 5 6 7 9
(1)求年推销金额y关于工作年限x的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:回归直线的斜率和截距的最小二乘法估计公式分别为=,a=-b.
16.(本小题15分)
某校组织本校2000名学生进行针对性检测(检测分为初试和复试),并随机抽取了100名学生的初试成绩,绘制了频率分布直方图,如图所示.
(1)根据频率分布直方图,求样本平均数的估计值;(同一组数据用该区间的中点值作代表)
(2)若所有学生的初试成绩X近似服从正态分布N(μ,σ2),其中μ为样本平均数的估计值,σ≈14.初试成绩不低于90分的学生才能参加复试,试估计能参加复试的人数.(四舍五入精确到整数).
附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ≤X≤μ+σ)=0.6827,P(μ-2σ≤X≤μ+2σ)=0.9545,P(μ-3σ≤X≤μ+3σ)=0.9973.
17.(本小题15分)
某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按照题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(Ⅰ)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(Ⅱ)请分析比较甲、乙两人谁的面试通过的可能性大?
18.(本小题17分)
从石墨中通过化学气相沉积法分离出石墨烯,升华后附着在材料上再结晶制成石墨烯发热膜,广泛应用于冬装衣服.现在有A材料、B材料可供选择,研究人员对附着在A材料、B材料上的石墨烯各做了100次再结晶试验,得到如下等高堆积条形图.
(1)根据等高堆积条形图,完成如下2×2列联表,并依据小概率值α=0.005的独立性检验,分析试验结果与材料是否有关:
A材料 B材料 合计
试验成功(单位:次)
试验失败(单位:次)
合计
(2)定义分类变量X,Y如下:,,以频率估计概率,求条件概率P(X=1|Y=0)和P(Y=0|X=0)的值.
附:,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
19.(本小题17分)
已知集合A={a1,a2,…,an}(0≤a1<a2<…<an,n≥2),若对任意的i,j∈N(1≤i≤j≤n),有ai+aj∈A或aj-ai∈A,则称集合A为完美集合.
(1)分别判断集合B={0,2,4,6}与C={1,2,3,4}是否为完美集合;
(2)当n=3时,若a2=2,求完美集合A;
(3)若集合D={a1,a2,…,a2024}(0≤a1<a2<…<a2024)为完美集合,记,求证:S2024=1012(a1012+a1013).
1.【答案】C
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】D
9.【答案】AB
10.【答案】ABD
11.【答案】BCD
12.【答案】{t|-7<t<2}
13.【答案】[0,4)
14.【答案】
15.【答案】解:(1)设所求的线性回归方程为=x+,
=(3+5+6+7+9)=6,
=(2+3+3+4+5)=3.4,
∴==,
=0.4,
∴年销售金额y产于工作年限x的线性回归方程为=0.5x+0.4.
(2)当x=11时,=0.5x+0.4=0.5×11+0.4=5.9(万元),
∴可以估计第6名推销员的年推销金额为5.9万元.
16.【答案】62;
46.
17.【答案】解:(Ⅰ)设甲正确完成面试的题数为ξ,则ξ的取值分别为1,2,3.…(1分)
P(ξ=1)==;P(ξ=2)==;P(ξ=3)==; …(3分)
考生甲正确完成题数ξ的分布列为
ξ 1 2 3
P
Eξ=1×+2×+3×=2.…(4分)
设乙正确完成面试的题数为η,则η取值分别为0,1,2,3.…(5分)
P(η=0)=;P(η=1)==,P(η=2)==,P(η=3)==.…(7分)
考生乙正确完成题数η的分布列为:
η 0 1 2 3
P
Eη=0×+1×+2×+3×=2.…(8分)
(Ⅱ)因为Dξ==,…(10分)
Dη=npq=.…(12分)
所以Dξ<Dη.
综上所述,从做对题数的数学期望考查,两人水平相当;从做对题数的方差考查,甲较稳定;从至少完成2道题的概率考查,甲获得面试通过的可能性大.…(13分)
18.【答案】解:(1)由堆积等高条形图得2×2列联表为:
A材料 B材料 合计
试验成功(单位:次) 80 60 140
试验失败(单位:次) 20 40 60
合计 100 100 200
零假设:试验结果与材料无关,
==9.524>7,
依据小概率值α=0.005的独立检验,推断假设不成立,
即试验结果与材料有关,此推断犯错误的概率不超过0.005.
(2)依题意得:
n(Y=0)=100,n(X=1,Y=0)=20,
∴P(X=1|Y=0)===,
n(X=0)=140,n(Y=0,X=0)=80,
∴P(Y=0|X=0)===.
19.【答案】集合B={0,2,4,6}为完美集合,C={1,2,3,4}不是完美集合;
A={0,2,4};
证明:因为a2024+a2024=2a2024>a2024,故a2024+a2024 D,
所以a2024-a2024=0∈D,则a1=0.
因为ai<ai+1(i=1,2, ,2023),
所以a2024+a2023>a2024+a2022> >a2024+a2>a2024,
所以a2024+ai D(i=2,3, ,2023),
所以a2024-ai∈D(i=2,3, ,2023).
因为0<a2024-a2023<a2024-a2022< <a2024-a2<a2024,
所以a2024-a2023=a2,a2024-a2022=a3, ,a2024-a2=a2023,
又因为a2024-a2024=a1,a2024-a1=a2024,
全部相加得2024a2024-(a1+a2+ a2024)=a1+a2+ +a2024,即2S2024=2024a2024,
所以S2024=1012a2024,又a2024=a1012+a1013,所以S2024=1012(a1012+a1013).
第1页,共1页
同课章节目录
