2024-2025学年江苏省扬州市江都实验中学八年级(下)第一次月考数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年江苏省扬州市江都实验中学八年级(下)第一次月考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 21:12:57 | ||
图片预览


文档简介
2024-2025学年江苏省扬州市江都实验中学八年级(下)第一次月考数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在下列与扬州有关的标识或简图中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.要调查下列问题,适合采用全面调查(普查)的是( )
A. 中央电视台《开学第一课》的收视率 B. 某城市居民6月份人均网上购物的次数
C. 即将发射的气象卫星的零部件质量 D. 某品牌新能源汽车的最大续航里程
3.如图是甲、乙两户居民家庭全年支出费用的扇形统计图.
根据统计图,下面对全年食品支出费用判断正确的是( )
A. 甲户比乙户多 B. 乙户比甲户少 C. 甲、乙两户一样 D. 无法确定哪一户多
4.能判定四边形ABCD为平行四边形的条件是( )
A. AB∥CD,∠C=∠A B. ∠A=∠B,∠C=∠D
C. AB∥CD,AD=BC D. AB=AD,CB=CD
5.正方形具有而矩形不具有的性质是( )
A. 对角线互相平分 B. 对角线相等
C. 对角线互相平分且相等 D. 对角线互相垂直
6.为了解我校八年级1200名学生期中数学考试情况,从中抽取了200名学生的数学成绩进行统计.下列判断:①这种调查方式是抽样调查;②1200名学生是总体;③每名学生的数学成绩是个体;④200名学生是总体的一个样本;⑤200是样本容量.其中正确的判断有( )
A. 1个 B. 2个 C. 3个 D. 4个
7.如图,在△ABC中,∠C=50°,将△ABC绕点A逆时针旋转到△A′B′C′,当点B′落在边BC上时,AC′∥BC,则∠B的度数为( )
A. 50°
B. 65°
C. 70°
D. 80°
8.如图,正方形ABCD的边长为15,AG=CH=12,BG=DH=9,连接GH,则线段GH的长是( )
A.
B. 3
C.
D. 4
二、填空题:本题共10小题,每小题3分,共30分。
9.某校八年级(1)班50名学生在一次数学测试中,优秀的占10%,在扇形统计图中,表示这部分同学的扇形圆心角的度数是______°.
10.春节前后,全球科技创新的顶流当属“DeepSeek”,在“DeepSeek”这个复合词中,字母“e”出现的频率是______.
11.已知△ABC中,AB=AC,求证:∠B<90°,用反证法证明:第一步是:假设______.
12.已知,点A(a,1)和点B(3,b)关于原点O对称,则a+b的值为 .
13.如图,在平行四边形ABCD中,AE平分∠BAD交CD边于点E,∠AED=35°,则∠B的度数是______°.
14.菱形的两条对角线长分别为和,则这个菱形的周长为__________.
15.如图,点O是矩形ABCD的对称中心,点E、F分别是边AB、CD上的点,且BE=DF,已知矩形ABCD的面积是20,那么图中阴影部分的面积为______.
16.平行四边形的一个内角平分线将对边分成3和5两个部分,则该平行四边形的周长是______.
17.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=12,BC=10,则EF的长是______.
18.如图,正方形的边ABCD长为2,M是BC的中点,N是AM上的动点,过点N作EF⊥AM分别交AB、CD于点E、F,当EM+AF取最小值时,AF的长是______.
三、解答题:本题共10小题,共96分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
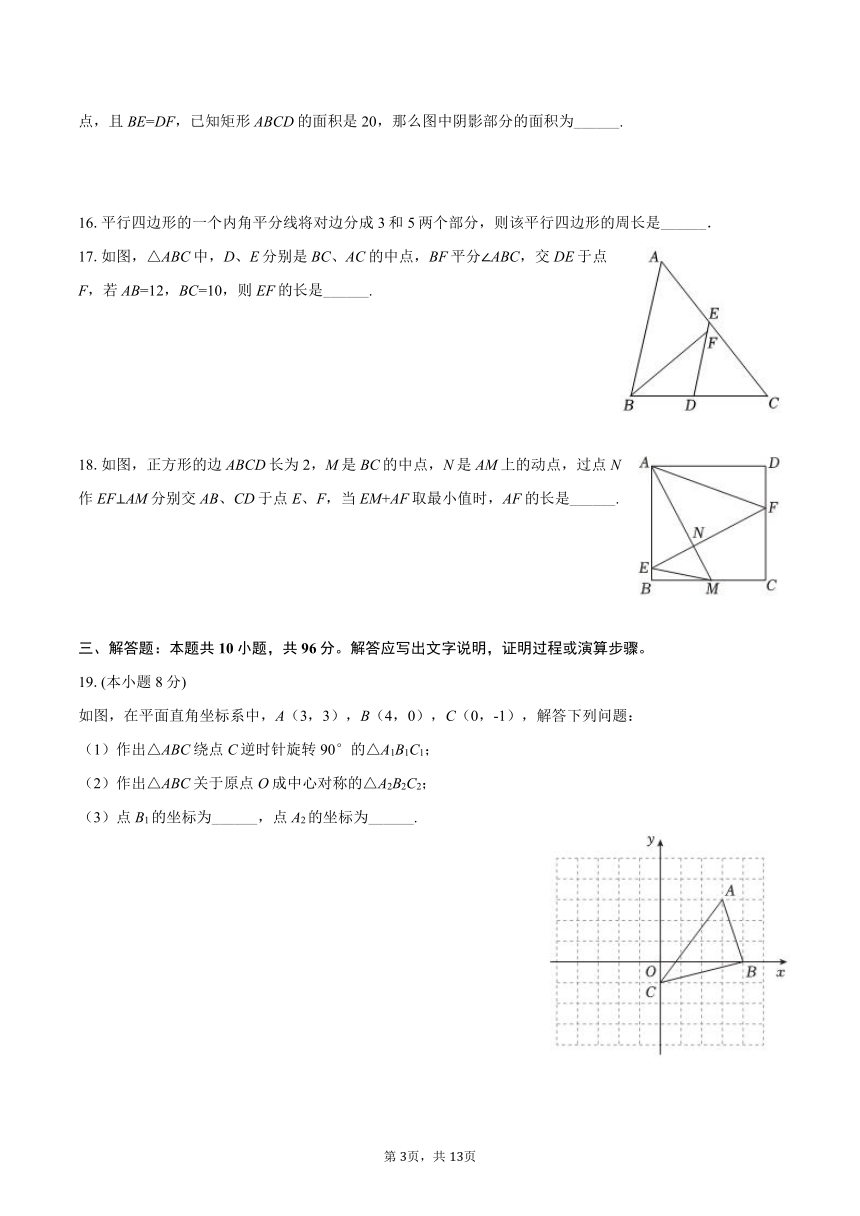
如图,在平面直角坐标系中,A(3,3),B(4,0),C(0,-1),解答下列问题:
(1)作出△ABC绕点C逆时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2;
(3)点B1的坐标为______,点A2的坐标为______.
20.(本小题8分)
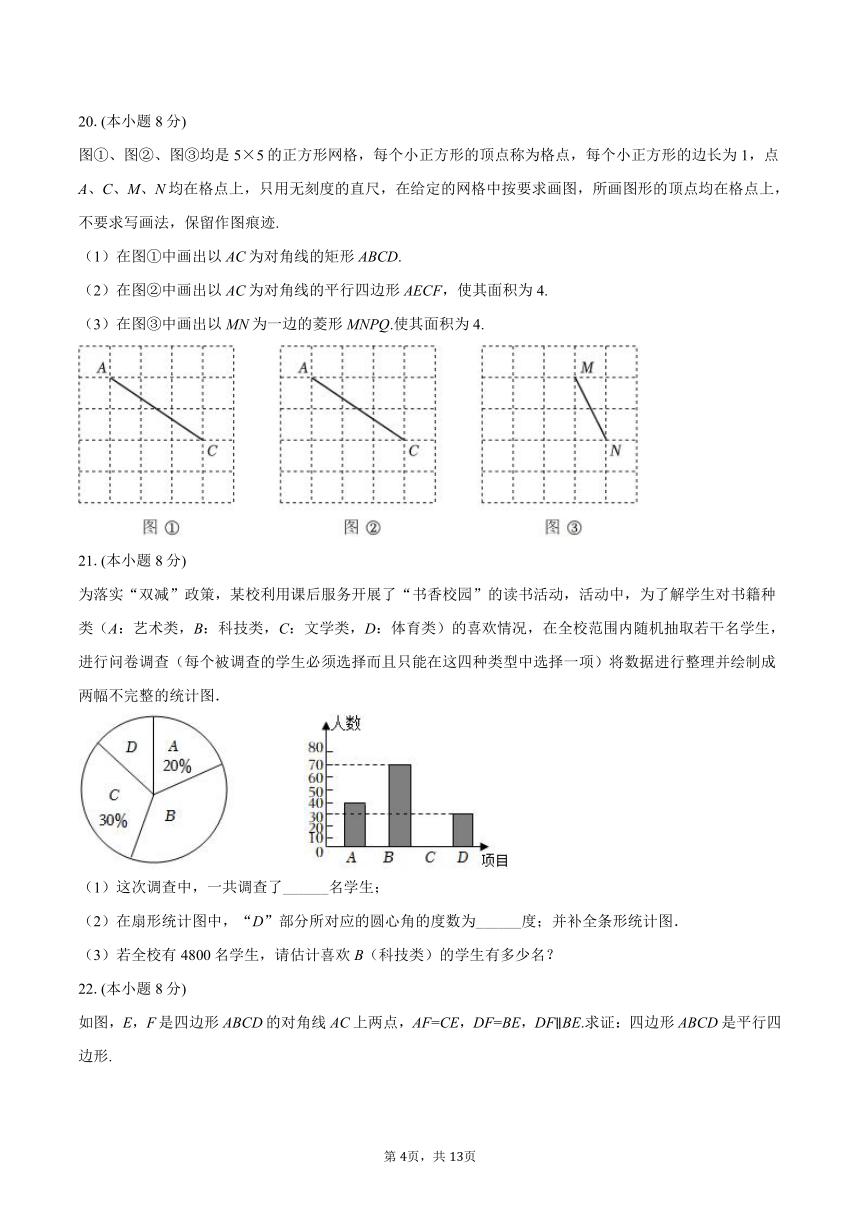
图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长为1,点A、C、M、N均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写画法,保留作图痕迹.
(1)在图①中画出以AC为对角线的矩形ABCD.
(2)在图②中画出以AC为对角线的平行四边形AECF,使其面积为4.
(3)在图③中画出以MN为一边的菱形MNPQ.使其面积为4.
21.(本小题8分)
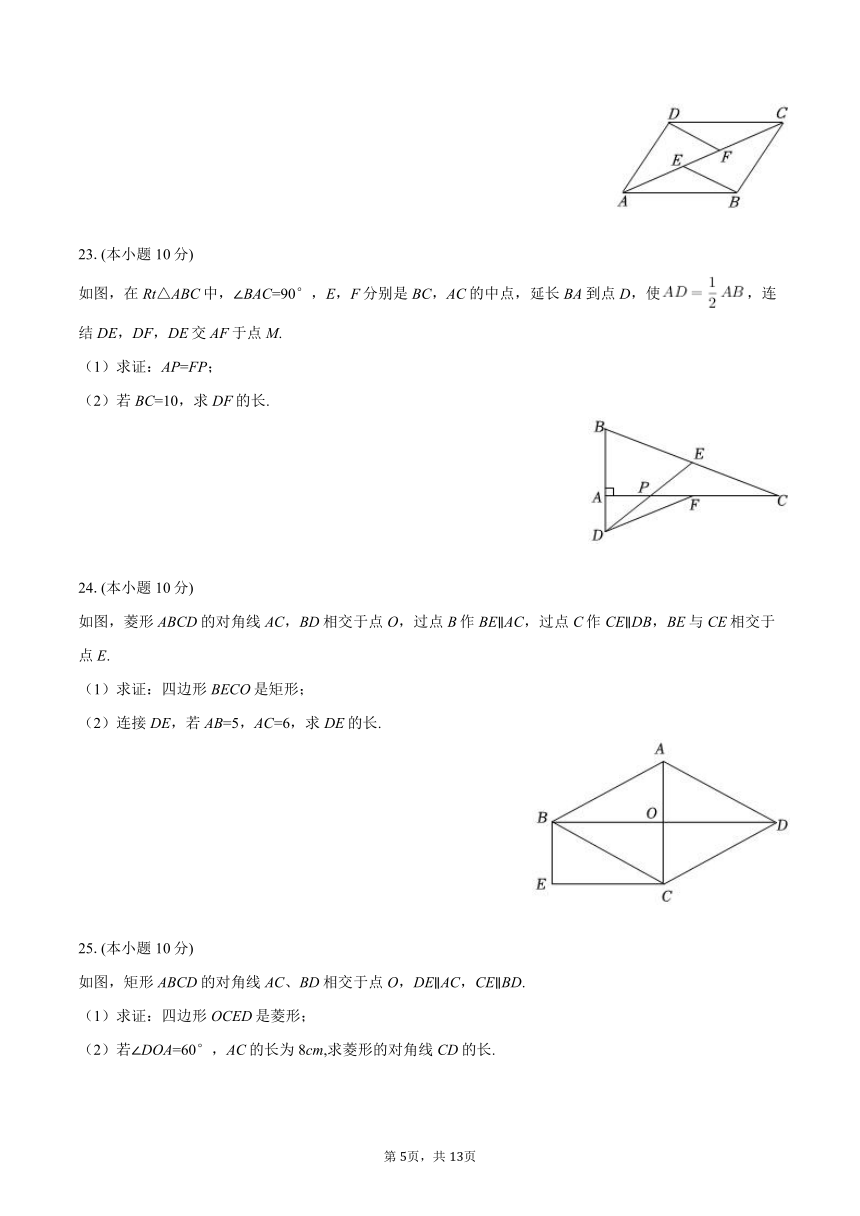
为落实“双减”政策,某校利用课后服务开展了“书香校园”的读书活动,活动中,为了解学生对书籍种类(A:艺术类,B:科技类,C:文学类,D:体育类)的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的学生必须选择而且只能在这四种类型中选择一项)将数据进行整理并绘制成两幅不完整的统计图.
(1)这次调查中,一共调查了______名学生;
(2)在扇形统计图中,“D”部分所对应的圆心角的度数为______度;并补全条形统计图.
(3)若全校有4800名学生,请估计喜欢B(科技类)的学生有多少名?
22.(本小题8分)
如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:四边形ABCD是平行四边形.
23.(本小题10分)
如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA到点D,使,连结DE,DF,DE交AF于点M.
(1)求证:AP=FP;
(2)若BC=10,求DF的长.
24.(本小题10分)
如图,菱形ABCD的对角线AC,BD相交于点O,过点B作BE∥AC,过点C作CE∥DB,BE与CE相交于点E.
(1)求证:四边形BECO是矩形;
(2)连接DE,若AB=5,AC=6,求DE的长.
25.(本小题10分)
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠DOA=60°,AC的长为8cm,求菱形的对角线CD的长.
26.(本小题10分)
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
27.(本小题12分)
实践操作
在矩形ABCD中,AB=10,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
初步思考
(1)若点P落在矩形ABCD的边AB上(如图①).
①当点P与点A重合时,∠DEF=______°;当点E与点A重合时,∠DEF=______°;
②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=8时的菱形EPFD的边长.
深入探究
(2)若点P落在矩形ABCD的内部,点E在边AD上且DE=4,点F在边DC上,请直接写出BP的最小值.
28.(本小题12分)
定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=______;
②如图2,平面直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是______;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,AB=3,BC=4,当△ADC是以AC为腰的等腰三角形时,请直接写出这个准矩形的面积.
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】C
9.【答案】36
10.【答案】0.5
11.【答案】∠B≥90°
12.【答案】-4
13.【答案】110
14.【答案】20
15.【答案】5
16.【答案】22或26
17.【答案】1
18.【答案】
19.【答案】
(-1,3);(-3,-3).
20.【答案】解:(1)如图①中,矩形ABCD即为所求;
(2)如图②中,平行四边形AECF即为所求;
(3)如图③中,菱形MNPQ即为所求.
21.【答案】解:(1)200 ;
(2)54;
C的人数是:200×30%=60(名),
补图如下:
(3)4800×=1680(名),
答:估计喜欢B(科技类)的学生有1680名.
22.【答案】证明:∵DF∥BE,
∴∠DFE=∠BEC,
∴在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS),
∴AD=CB,∠DAF=∠BCE,
∴AD∥CB,
∴四边形ABCD是平行四边形.
23.【答案】(1)证明:连接EF,AE.
∵点E,F分别为BC,AC的中点,
∴EF∥AB,EF=AB.
又∵AD=AB,
∴EF=AD.
又∵EF∥AD,
∴四边形AEFD是平行四边形.
∴AF与DE互相平分,
∴AP=FP;
(2)解:在Rt△ABC中,
∵E为BC的中点,BC=10,
∴AE=BC=5.
又∵四边形AEFD是平行四边形,
∴DF=AE=5.
24.【答案】(1)证明:∵BE∥AC,CE∥DB,
∴四边形BECO是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠BOC=90°,
∴平行四边形BECO是矩形;
(2)解:如图,
∵四边形ABCD是菱形,AC=6,
∴OA=OC===3,OB=OD,AC⊥BD,
∴,
∴BD=2OB=8.
∵四边形BECO是矩形,
∴BE=OC=3.
∴.
25.【答案】(1)证明:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,
∴OC=OD=OA,
∴四边形CODE是菱形;
(2)解:∵∠DOA=60°,OA=DO,
∴△AOD是等边三角形,
∴AD=AO=AC=4cm,
∴DC===4(cm).
26.【答案】解:(1)当四边形ABQP是矩形时,BQ=AP,即:t=8-t,
解得t=4.
答:当t=4时,四边形ABQP是矩形;
(2)设t秒后,四边形AQCP是菱形
当AQ=CQ,即=8-t时,四边形AQCP为菱形.
解得:t=3.
答:当t=3时,四边形AQCP是菱形;
(3)当t=3时,CQ=5,则周长为:4CQ=20cm,
面积为:4×8-2××3×4=20(cm2).
27.【答案】①90,45;
②证明见解析过程,菱形EPFD的边长为;
BP的最小值为2-4.
28.【答案】①;
②(3,5)或(5,3);
见解析;
这个准矩形的面积是3+或3+2.
第2页,共2页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在下列与扬州有关的标识或简图中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.要调查下列问题,适合采用全面调查(普查)的是( )
A. 中央电视台《开学第一课》的收视率 B. 某城市居民6月份人均网上购物的次数
C. 即将发射的气象卫星的零部件质量 D. 某品牌新能源汽车的最大续航里程
3.如图是甲、乙两户居民家庭全年支出费用的扇形统计图.
根据统计图,下面对全年食品支出费用判断正确的是( )
A. 甲户比乙户多 B. 乙户比甲户少 C. 甲、乙两户一样 D. 无法确定哪一户多
4.能判定四边形ABCD为平行四边形的条件是( )
A. AB∥CD,∠C=∠A B. ∠A=∠B,∠C=∠D
C. AB∥CD,AD=BC D. AB=AD,CB=CD
5.正方形具有而矩形不具有的性质是( )
A. 对角线互相平分 B. 对角线相等
C. 对角线互相平分且相等 D. 对角线互相垂直
6.为了解我校八年级1200名学生期中数学考试情况,从中抽取了200名学生的数学成绩进行统计.下列判断:①这种调查方式是抽样调查;②1200名学生是总体;③每名学生的数学成绩是个体;④200名学生是总体的一个样本;⑤200是样本容量.其中正确的判断有( )
A. 1个 B. 2个 C. 3个 D. 4个
7.如图,在△ABC中,∠C=50°,将△ABC绕点A逆时针旋转到△A′B′C′,当点B′落在边BC上时,AC′∥BC,则∠B的度数为( )
A. 50°
B. 65°
C. 70°
D. 80°
8.如图,正方形ABCD的边长为15,AG=CH=12,BG=DH=9,连接GH,则线段GH的长是( )
A.
B. 3
C.
D. 4
二、填空题:本题共10小题,每小题3分,共30分。
9.某校八年级(1)班50名学生在一次数学测试中,优秀的占10%,在扇形统计图中,表示这部分同学的扇形圆心角的度数是______°.
10.春节前后,全球科技创新的顶流当属“DeepSeek”,在“DeepSeek”这个复合词中,字母“e”出现的频率是______.
11.已知△ABC中,AB=AC,求证:∠B<90°,用反证法证明:第一步是:假设______.
12.已知,点A(a,1)和点B(3,b)关于原点O对称,则a+b的值为 .
13.如图,在平行四边形ABCD中,AE平分∠BAD交CD边于点E,∠AED=35°,则∠B的度数是______°.
14.菱形的两条对角线长分别为和,则这个菱形的周长为__________.
15.如图,点O是矩形ABCD的对称中心,点E、F分别是边AB、CD上的点,且BE=DF,已知矩形ABCD的面积是20,那么图中阴影部分的面积为______.
16.平行四边形的一个内角平分线将对边分成3和5两个部分,则该平行四边形的周长是______.
17.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=12,BC=10,则EF的长是______.
18.如图,正方形的边ABCD长为2,M是BC的中点,N是AM上的动点,过点N作EF⊥AM分别交AB、CD于点E、F,当EM+AF取最小值时,AF的长是______.
三、解答题:本题共10小题,共96分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
如图,在平面直角坐标系中,A(3,3),B(4,0),C(0,-1),解答下列问题:
(1)作出△ABC绕点C逆时针旋转90°的△A1B1C1;
(2)作出△ABC关于原点O成中心对称的△A2B2C2;
(3)点B1的坐标为______,点A2的坐标为______.
20.(本小题8分)
图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长为1,点A、C、M、N均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写画法,保留作图痕迹.
(1)在图①中画出以AC为对角线的矩形ABCD.
(2)在图②中画出以AC为对角线的平行四边形AECF,使其面积为4.
(3)在图③中画出以MN为一边的菱形MNPQ.使其面积为4.
21.(本小题8分)
为落实“双减”政策,某校利用课后服务开展了“书香校园”的读书活动,活动中,为了解学生对书籍种类(A:艺术类,B:科技类,C:文学类,D:体育类)的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的学生必须选择而且只能在这四种类型中选择一项)将数据进行整理并绘制成两幅不完整的统计图.
(1)这次调查中,一共调查了______名学生;
(2)在扇形统计图中,“D”部分所对应的圆心角的度数为______度;并补全条形统计图.
(3)若全校有4800名学生,请估计喜欢B(科技类)的学生有多少名?
22.(本小题8分)
如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:四边形ABCD是平行四边形.
23.(本小题10分)
如图,在Rt△ABC中,∠BAC=90°,E,F分别是BC,AC的中点,延长BA到点D,使,连结DE,DF,DE交AF于点M.
(1)求证:AP=FP;
(2)若BC=10,求DF的长.
24.(本小题10分)
如图,菱形ABCD的对角线AC,BD相交于点O,过点B作BE∥AC,过点C作CE∥DB,BE与CE相交于点E.
(1)求证:四边形BECO是矩形;
(2)连接DE,若AB=5,AC=6,求DE的长.
25.(本小题10分)
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠DOA=60°,AC的长为8cm,求菱形的对角线CD的长.
26.(本小题10分)
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
27.(本小题12分)
实践操作
在矩形ABCD中,AB=10,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
初步思考
(1)若点P落在矩形ABCD的边AB上(如图①).
①当点P与点A重合时,∠DEF=______°;当点E与点A重合时,∠DEF=______°;
②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=8时的菱形EPFD的边长.
深入探究
(2)若点P落在矩形ABCD的内部,点E在边AD上且DE=4,点F在边DC上,请直接写出BP的最小值.
28.(本小题12分)
定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=______;
②如图2,平面直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是______;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,AB=3,BC=4,当△ADC是以AC为腰的等腰三角形时,请直接写出这个准矩形的面积.
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】C
9.【答案】36
10.【答案】0.5
11.【答案】∠B≥90°
12.【答案】-4
13.【答案】110
14.【答案】20
15.【答案】5
16.【答案】22或26
17.【答案】1
18.【答案】
19.【答案】
(-1,3);(-3,-3).
20.【答案】解:(1)如图①中,矩形ABCD即为所求;
(2)如图②中,平行四边形AECF即为所求;
(3)如图③中,菱形MNPQ即为所求.
21.【答案】解:(1)200 ;
(2)54;
C的人数是:200×30%=60(名),
补图如下:
(3)4800×=1680(名),
答:估计喜欢B(科技类)的学生有1680名.
22.【答案】证明:∵DF∥BE,
∴∠DFE=∠BEC,
∴在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS),
∴AD=CB,∠DAF=∠BCE,
∴AD∥CB,
∴四边形ABCD是平行四边形.
23.【答案】(1)证明:连接EF,AE.
∵点E,F分别为BC,AC的中点,
∴EF∥AB,EF=AB.
又∵AD=AB,
∴EF=AD.
又∵EF∥AD,
∴四边形AEFD是平行四边形.
∴AF与DE互相平分,
∴AP=FP;
(2)解:在Rt△ABC中,
∵E为BC的中点,BC=10,
∴AE=BC=5.
又∵四边形AEFD是平行四边形,
∴DF=AE=5.
24.【答案】(1)证明:∵BE∥AC,CE∥DB,
∴四边形BECO是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠BOC=90°,
∴平行四边形BECO是矩形;
(2)解:如图,
∵四边形ABCD是菱形,AC=6,
∴OA=OC===3,OB=OD,AC⊥BD,
∴,
∴BD=2OB=8.
∵四边形BECO是矩形,
∴BE=OC=3.
∴.
25.【答案】(1)证明:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,
∴OC=OD=OA,
∴四边形CODE是菱形;
(2)解:∵∠DOA=60°,OA=DO,
∴△AOD是等边三角形,
∴AD=AO=AC=4cm,
∴DC===4(cm).
26.【答案】解:(1)当四边形ABQP是矩形时,BQ=AP,即:t=8-t,
解得t=4.
答:当t=4时,四边形ABQP是矩形;
(2)设t秒后,四边形AQCP是菱形
当AQ=CQ,即=8-t时,四边形AQCP为菱形.
解得:t=3.
答:当t=3时,四边形AQCP是菱形;
(3)当t=3时,CQ=5,则周长为:4CQ=20cm,
面积为:4×8-2××3×4=20(cm2).
27.【答案】①90,45;
②证明见解析过程,菱形EPFD的边长为;
BP的最小值为2-4.
28.【答案】①;
②(3,5)或(5,3);
见解析;
这个准矩形的面积是3+或3+2.
第2页,共2页
同课章节目录
