2025年陕西省西安六中中考数学六模试卷(含部分答案)
文档属性
| 名称 | 2025年陕西省西安六中中考数学六模试卷(含部分答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览


文档简介
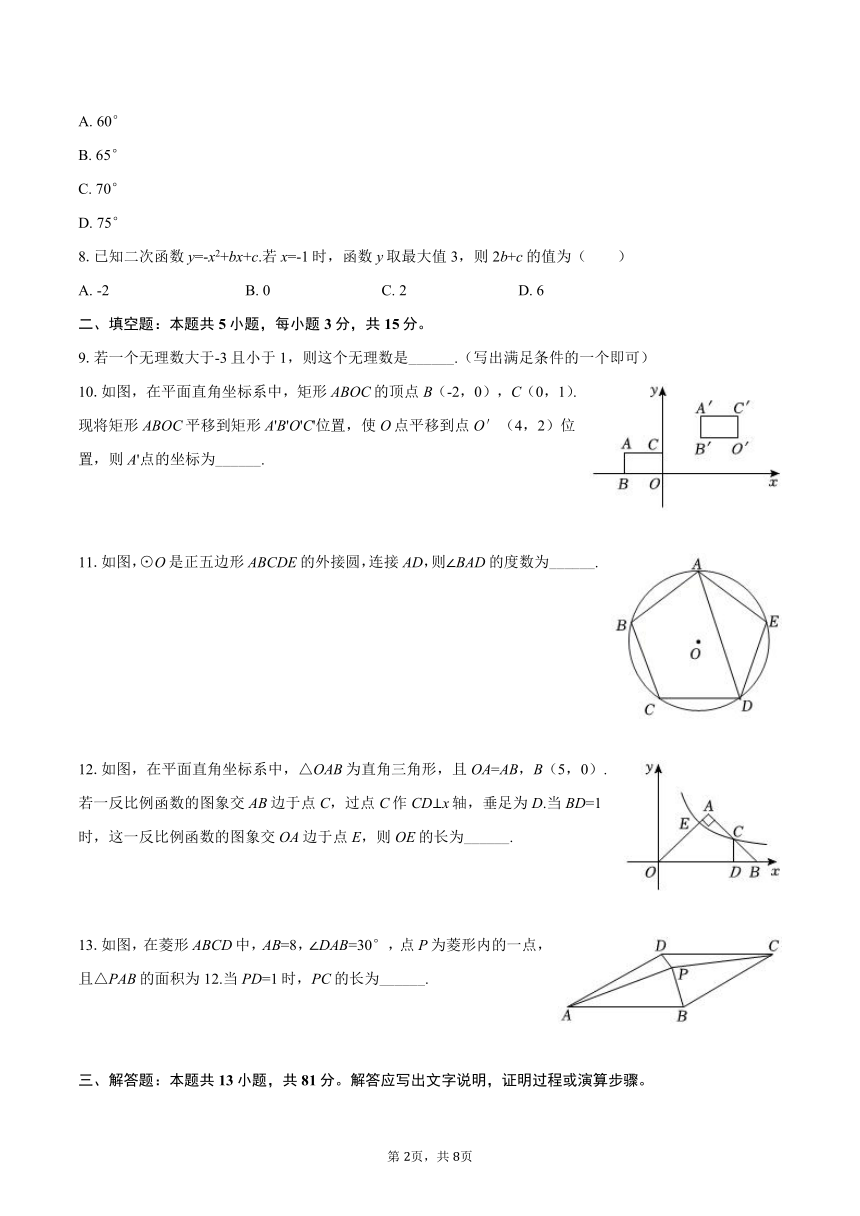
2025年陕西省西安六中中考数学六模试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.计算-3+2的值是( )
A. -5 B. -1 C. 1 D. -6
2.如图,AB∥CD,∠A=44°,∠C=32°,则∠AEC的度数为( )
A. 12°
B. 72°
C. 76°
D. 104°
3.计算:2xy2 (-3x2y)=( )
A. -6x2y2 B. -6x3y3 C. 6x2y2 D. 6x3y3
4.如图,在Rt△ABC中,∠C=90°,AD为BC边上的中线.若AC=3,CD=2,则sinB的值为( )
A.
B.
C.
D.
5.对于正比例函数y=-2x和一次函数y=x-m,若m>0,则这两个函数图象的交点一定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6.如图,在 ABCD中,对角线AC,BD相交于点O,AB=4,BC=6,过点O作OE∥AB交BC于点E,延长EC到点F,使CF=2EC,连接OF交CD于点G,则DG的长为( )
A. 2 B. C. D.
7.如图,在⊙O中,AB是⊙O的直径,C是⊙O上的一点,连接AC,BC,过点O作OD∥CB交⊙O于点D,连接CD,AD.若∠CAB=40°,则∠ACD的度数为( )
A. 60°
B. 65°
C. 70°
D. 75°
8.已知二次函数y=-x2+bx+c.若x=-1时,函数y取最大值3,则2b+c的值为( )
A. -2 B. 0 C. 2 D. 6
二、填空题:本题共5小题,每小题3分,共15分。
9.若一个无理数大于-3且小于1,则这个无理数是______.(写出满足条件的一个即可)
10.如图,在平面直角坐标系中,矩形ABOC的顶点B(-2,0),C(0,1).现将矩形ABOC平移到矩形A'B'O'C'位置,使O点平移到点O′(4,2)位置,则A'点的坐标为______.
11.如图,⊙O是正五边形ABCDE的外接圆,连接AD,则∠BAD的度数为______.
12.如图,在平面直角坐标系中,△OAB为直角三角形,且OA=AB,B(5,0).若一反比例函数的图象交AB边于点C,过点C作CD⊥x轴,垂足为D.当BD=1时,这一反比例函数的图象交OA边于点E,则OE的长为______.
13.如图,在菱形ABCD中,AB=8,∠DAB=30°,点P为菱形内的一点,且△PAB的面积为12.当PD=1时,PC的长为______.
三、解答题:本题共13小题,共81分。解答应写出文字说明,证明过程或演算步骤。
14.(本小题5分)
计算:.
15.(本小题5分)
解不等式:,并把解集在数轴上表示出来.
16.(本小题5分)
解方程.
17.(本小题5分)
如图,在△ABC中,AB=AC=5,BC=6,请用尺规作图法,在边BC上求作一点D,使得AD=4.(保留作图痕迹,不写作法)
18.(本小题5分)
如图,A,E,F,B在同一条直线上,点C在DF上,∠A=∠D,∠ACF=∠B,AC=DF.求证:AB=DE.
19.(本小题5分)
3月12日是植树节,许多家庭积极参与植树活动,为建设美丽中国,共同谱写人与自然和谐共生的中国式现代化新篇章.在一次家庭植树活动中,甲组家庭植树的棵数比乙组家庭多20%,乙组家庭植树的棵数比甲组家庭的一半多10棵,求甲、乙两组家庭共植树多少棵.
20.(本小题5分)
李华和张丽相约一起到图书馆学习,她们被分到同一张书桌,书桌有A,B,C,D四个座位,如图所示.
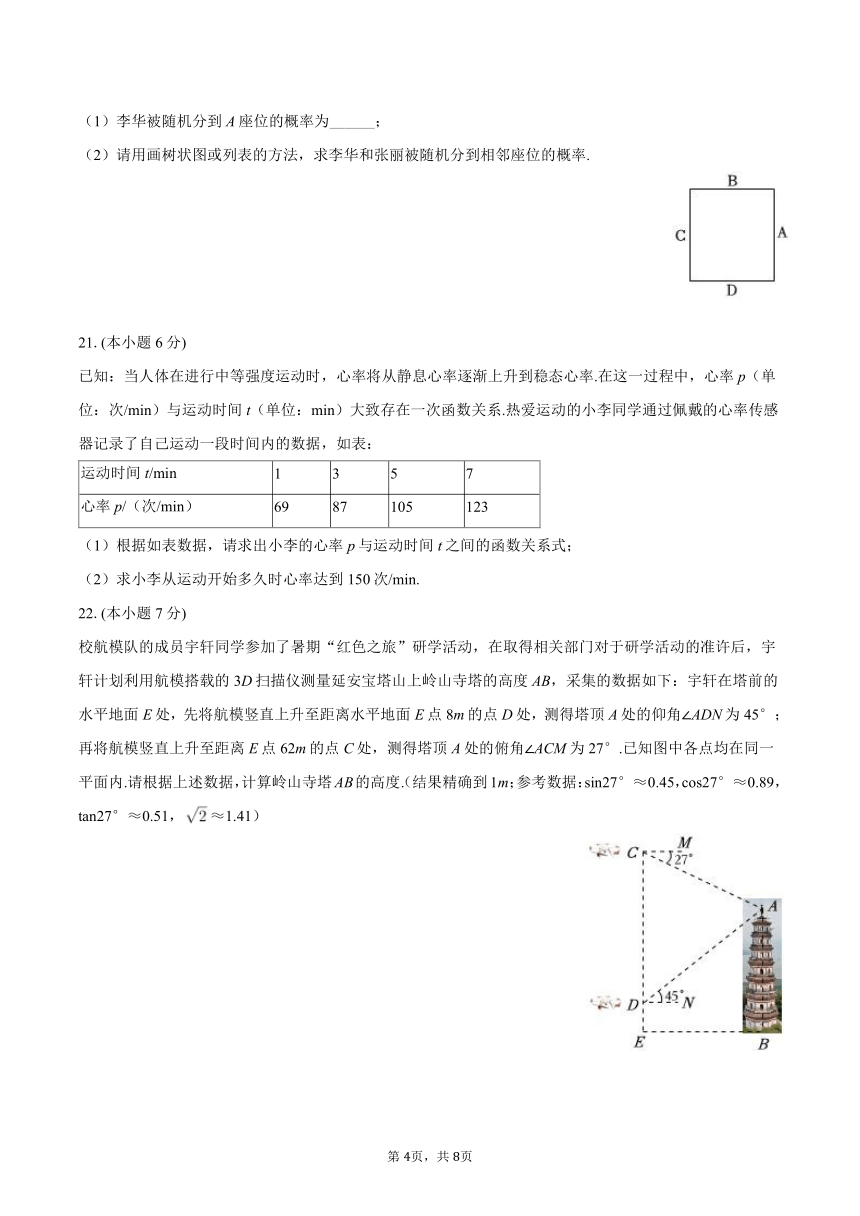
(1)李华被随机分到A座位的概率为______;
(2)请用画树状图或列表的方法,求李华和张丽被随机分到相邻座位的概率.
21.(本小题6分)
已知:当人体在进行中等强度运动时,心率将从静息心率逐渐上升到稳态心率.在这一过程中,心率p(单位:次/min)与运动时间t(单位:min)大致存在一次函数关系.热爱运动的小李同学通过佩戴的心率传感器记录了自己运动一段时间内的数据,如表:
运动时间t/min 1 3 5 7
心率p/(次/min) 69 87 105 123
(1)根据如表数据,请求出小李的心率p与运动时间t之间的函数关系式;
(2)求小李从运动开始多久时心率达到150次/min.
22.(本小题7分)
校航模队的成员宇轩同学参加了暑期“红色之旅”研学活动,在取得相关部门对于研学活动的准许后,宇轩计划利用航模搭载的3D扫描仪测量延安宝塔山上岭山寺塔的高度AB,采集的数据如下:宇轩在塔前的水平地面E处,先将航模竖直上升至距离水平地面E点8m的点D处,测得塔顶A处的仰角∠ADN为45°;再将航模竖直上升至距离E点62m的点C处,测得塔顶A处的俯角∠ACM为27°.已知图中各点均在同一平面内.请根据上述数据,计算岭山寺塔AB的高度.(结果精确到1m;参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,≈1.41)
23.(本小题7分)
某校在3月5日开展了“学习雷锋精神”的主题教育活动,向全校2400名学生发起了“学习雷锋好榜样,人人助力福利院”爱心捐款活动.为了解学生的献爱心情况,校学生会随机调查了部分学生的捐款金额,并绘制了如下不完整的统计图:
请根据以上信息,解答下列问题:
(1)请补全条形统计图;
(2)扇形统计图中“5元”所对应扇形的圆心角度数是______,本次调查学生捐款金额的众数为______元;
(3)估计该校本次爱心捐款的总金额.
24.(本小题8分)
如图,△ABC内接于⊙O,AB=AC,连接BO,CO,延长BO交AC于点D,交⊙O的切线AE于点E.
(1)求证:AE∥BC;
(2)若BC=8,OC=5,求AD的长.
25.(本小题8分)
周末,小明与几个同学去户外玩弹力球.小明站在O点处并在距地面2m高的A处抛出一个弹力球,弹力球的运动路线可看作抛物线L1的一部分,弹力球在距离小明水平距离4m处时到达最高点D,此时弹力球距离地面6m,当弹力球落在斜坡上的点B处时回弹,回弹后的运动路线可看作抛物线L2的一部分,其中抛物线L2的开口大小和方向与抛物线L1相同,且在距离地面3m处到达最高点.已知斜坡与地面的夹角为45°,斜坡底部点C与点O的距离OC为6m,CB为.
(1)求抛物线L1的函数表达式及点B的坐标;
(2)若弹力球从点B回弹后,落在地面E点处,求OE的长.
26.(本小题10分)
问题提出
(1)如图①,线段AB=b,点C为平面内一动点,连接AC,BC.若AC=a(b>a),则线段BC的最小值为______(用含a,b的式子表示).
问题探究
(2)如图②,某村街道AE的右侧有一块开阔的空地,当地政府为了弘扬传统文化、打造当地旅游特色村,将在此处建设一处文化街区.已知:空地边界AD与街道AE的夹角∠DAE为45°,且AE∥CD,AE⊥AB,AD=300m,计划在空地的一角打造以“非遗文化创意手工展”为主题的长廊BC,长度为60m,若空地边界AD上的点P为出入口,点M,N分别为两个休息点,且AM=150m,N为BC的中点,出入口P到休息点M,N各有一条通道MP,NP.请问:是否存在满足条件的点P,使得通道MP,NP的长度之和最短?若存在,求此时MP,NP的长度之和;若不存在,请说明理由.(图中各点均在同一平面内,街道AE与通道MP,NP的宽、休息点及出入口的大小均忽略不计,结果保留根号)
1.【答案】B
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】(答案不唯一)
10.【答案】(2,3)
11.【答案】72°
12.【答案】2
13.【答案】
14.【答案】-1.
15.【答案】x>-1.
16.【答案】x=5.
17.【答案】见解答.
18.【答案】证明见解答过程.
19.【答案】甲、乙两组家庭共植树55棵.
20.【答案】.
.
21.【答案】p=9t+60;
10 min.
22.【答案】岭山寺塔AB的高度约为44m.
23.【答案】见解答;
144°,5;
10176元.
24.【答案】见解答;
.
25.【答案】抛物线L1的函数表达式为y=-(x-4)2+6,点B坐标为(8,2); OE的长为(6-2)m.
26.【答案】b-a;
存在满足条件的点P,使得通道MP,NP的长度之和最短,此时MP,NP的长度之和为120cm.
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.计算-3+2的值是( )
A. -5 B. -1 C. 1 D. -6
2.如图,AB∥CD,∠A=44°,∠C=32°,则∠AEC的度数为( )
A. 12°
B. 72°
C. 76°
D. 104°
3.计算:2xy2 (-3x2y)=( )
A. -6x2y2 B. -6x3y3 C. 6x2y2 D. 6x3y3
4.如图,在Rt△ABC中,∠C=90°,AD为BC边上的中线.若AC=3,CD=2,则sinB的值为( )
A.
B.
C.
D.
5.对于正比例函数y=-2x和一次函数y=x-m,若m>0,则这两个函数图象的交点一定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6.如图,在 ABCD中,对角线AC,BD相交于点O,AB=4,BC=6,过点O作OE∥AB交BC于点E,延长EC到点F,使CF=2EC,连接OF交CD于点G,则DG的长为( )
A. 2 B. C. D.
7.如图,在⊙O中,AB是⊙O的直径,C是⊙O上的一点,连接AC,BC,过点O作OD∥CB交⊙O于点D,连接CD,AD.若∠CAB=40°,则∠ACD的度数为( )
A. 60°
B. 65°
C. 70°
D. 75°
8.已知二次函数y=-x2+bx+c.若x=-1时,函数y取最大值3,则2b+c的值为( )
A. -2 B. 0 C. 2 D. 6
二、填空题:本题共5小题,每小题3分,共15分。
9.若一个无理数大于-3且小于1,则这个无理数是______.(写出满足条件的一个即可)
10.如图,在平面直角坐标系中,矩形ABOC的顶点B(-2,0),C(0,1).现将矩形ABOC平移到矩形A'B'O'C'位置,使O点平移到点O′(4,2)位置,则A'点的坐标为______.
11.如图,⊙O是正五边形ABCDE的外接圆,连接AD,则∠BAD的度数为______.
12.如图,在平面直角坐标系中,△OAB为直角三角形,且OA=AB,B(5,0).若一反比例函数的图象交AB边于点C,过点C作CD⊥x轴,垂足为D.当BD=1时,这一反比例函数的图象交OA边于点E,则OE的长为______.
13.如图,在菱形ABCD中,AB=8,∠DAB=30°,点P为菱形内的一点,且△PAB的面积为12.当PD=1时,PC的长为______.
三、解答题:本题共13小题,共81分。解答应写出文字说明,证明过程或演算步骤。
14.(本小题5分)
计算:.
15.(本小题5分)
解不等式:,并把解集在数轴上表示出来.
16.(本小题5分)
解方程.
17.(本小题5分)
如图,在△ABC中,AB=AC=5,BC=6,请用尺规作图法,在边BC上求作一点D,使得AD=4.(保留作图痕迹,不写作法)
18.(本小题5分)
如图,A,E,F,B在同一条直线上,点C在DF上,∠A=∠D,∠ACF=∠B,AC=DF.求证:AB=DE.
19.(本小题5分)
3月12日是植树节,许多家庭积极参与植树活动,为建设美丽中国,共同谱写人与自然和谐共生的中国式现代化新篇章.在一次家庭植树活动中,甲组家庭植树的棵数比乙组家庭多20%,乙组家庭植树的棵数比甲组家庭的一半多10棵,求甲、乙两组家庭共植树多少棵.
20.(本小题5分)
李华和张丽相约一起到图书馆学习,她们被分到同一张书桌,书桌有A,B,C,D四个座位,如图所示.
(1)李华被随机分到A座位的概率为______;
(2)请用画树状图或列表的方法,求李华和张丽被随机分到相邻座位的概率.
21.(本小题6分)
已知:当人体在进行中等强度运动时,心率将从静息心率逐渐上升到稳态心率.在这一过程中,心率p(单位:次/min)与运动时间t(单位:min)大致存在一次函数关系.热爱运动的小李同学通过佩戴的心率传感器记录了自己运动一段时间内的数据,如表:
运动时间t/min 1 3 5 7
心率p/(次/min) 69 87 105 123
(1)根据如表数据,请求出小李的心率p与运动时间t之间的函数关系式;
(2)求小李从运动开始多久时心率达到150次/min.
22.(本小题7分)
校航模队的成员宇轩同学参加了暑期“红色之旅”研学活动,在取得相关部门对于研学活动的准许后,宇轩计划利用航模搭载的3D扫描仪测量延安宝塔山上岭山寺塔的高度AB,采集的数据如下:宇轩在塔前的水平地面E处,先将航模竖直上升至距离水平地面E点8m的点D处,测得塔顶A处的仰角∠ADN为45°;再将航模竖直上升至距离E点62m的点C处,测得塔顶A处的俯角∠ACM为27°.已知图中各点均在同一平面内.请根据上述数据,计算岭山寺塔AB的高度.(结果精确到1m;参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,≈1.41)
23.(本小题7分)
某校在3月5日开展了“学习雷锋精神”的主题教育活动,向全校2400名学生发起了“学习雷锋好榜样,人人助力福利院”爱心捐款活动.为了解学生的献爱心情况,校学生会随机调查了部分学生的捐款金额,并绘制了如下不完整的统计图:
请根据以上信息,解答下列问题:
(1)请补全条形统计图;
(2)扇形统计图中“5元”所对应扇形的圆心角度数是______,本次调查学生捐款金额的众数为______元;
(3)估计该校本次爱心捐款的总金额.
24.(本小题8分)
如图,△ABC内接于⊙O,AB=AC,连接BO,CO,延长BO交AC于点D,交⊙O的切线AE于点E.
(1)求证:AE∥BC;
(2)若BC=8,OC=5,求AD的长.
25.(本小题8分)
周末,小明与几个同学去户外玩弹力球.小明站在O点处并在距地面2m高的A处抛出一个弹力球,弹力球的运动路线可看作抛物线L1的一部分,弹力球在距离小明水平距离4m处时到达最高点D,此时弹力球距离地面6m,当弹力球落在斜坡上的点B处时回弹,回弹后的运动路线可看作抛物线L2的一部分,其中抛物线L2的开口大小和方向与抛物线L1相同,且在距离地面3m处到达最高点.已知斜坡与地面的夹角为45°,斜坡底部点C与点O的距离OC为6m,CB为.
(1)求抛物线L1的函数表达式及点B的坐标;
(2)若弹力球从点B回弹后,落在地面E点处,求OE的长.
26.(本小题10分)
问题提出
(1)如图①,线段AB=b,点C为平面内一动点,连接AC,BC.若AC=a(b>a),则线段BC的最小值为______(用含a,b的式子表示).
问题探究
(2)如图②,某村街道AE的右侧有一块开阔的空地,当地政府为了弘扬传统文化、打造当地旅游特色村,将在此处建设一处文化街区.已知:空地边界AD与街道AE的夹角∠DAE为45°,且AE∥CD,AE⊥AB,AD=300m,计划在空地的一角打造以“非遗文化创意手工展”为主题的长廊BC,长度为60m,若空地边界AD上的点P为出入口,点M,N分别为两个休息点,且AM=150m,N为BC的中点,出入口P到休息点M,N各有一条通道MP,NP.请问:是否存在满足条件的点P,使得通道MP,NP的长度之和最短?若存在,求此时MP,NP的长度之和;若不存在,请说明理由.(图中各点均在同一平面内,街道AE与通道MP,NP的宽、休息点及出入口的大小均忽略不计,结果保留根号)
1.【答案】B
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】(答案不唯一)
10.【答案】(2,3)
11.【答案】72°
12.【答案】2
13.【答案】
14.【答案】-1.
15.【答案】x>-1.
16.【答案】x=5.
17.【答案】见解答.
18.【答案】证明见解答过程.
19.【答案】甲、乙两组家庭共植树55棵.
20.【答案】.
.
21.【答案】p=9t+60;
10 min.
22.【答案】岭山寺塔AB的高度约为44m.
23.【答案】见解答;
144°,5;
10176元.
24.【答案】见解答;
.
25.【答案】抛物线L1的函数表达式为y=-(x-4)2+6,点B坐标为(8,2); OE的长为(6-2)m.
26.【答案】b-a;
存在满足条件的点P,使得通道MP,NP的长度之和最短,此时MP,NP的长度之和为120cm.
第1页,共1页
同课章节目录
