2024-2025学年山东省淄博市博山区六年级(下)期末数学试卷(五四学制)(含简单答案)
文档属性
| 名称 | 2024-2025学年山东省淄博市博山区六年级(下)期末数学试卷(五四学制)(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 654.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 11:48:30 | ||
图片预览


文档简介
2024-2025学年山东省淄博市博山区六年级(下)期末数学试卷(五四学制)
一、选择题:本大题共12个小题,每小题4分,共48分。在每小题所给出的四个选项中,只有一项是符合题目要求的。
1.(4分)如图,下列给出的直线、射线和线段中能相交的是( )
A.a与b B.c与d C.b与d D.a与c
2.(4分)x=3是下列哪个方程的解( )
A.3x﹣1=2 B.2x﹣3=﹣x C.|x﹣3|=1 D.(x﹣1)2=4
3.(4分)如图,直线AB,CD相交于点O,若∠1=∠2=40°,则∠BOE的度数是( )
A.40° B.60° C.80° D.100°
4.(4分)用科学记数法表示的数3×10﹣3在数轴上的位置最接近( )
A.点P B.点Q C.点M D.点N
5.(4分)下列运算中,不正确的是( )
A.(﹣a3)2=a9 B.a3+a3=2a3 C.a2 a3=a5 D.2a3÷a2=2a
6.(4分)观察图1,若天平保持平衡,在图2天平的右盘中需放入( )个〇才能使其平衡.
A.5 B.6 C.7 D.8
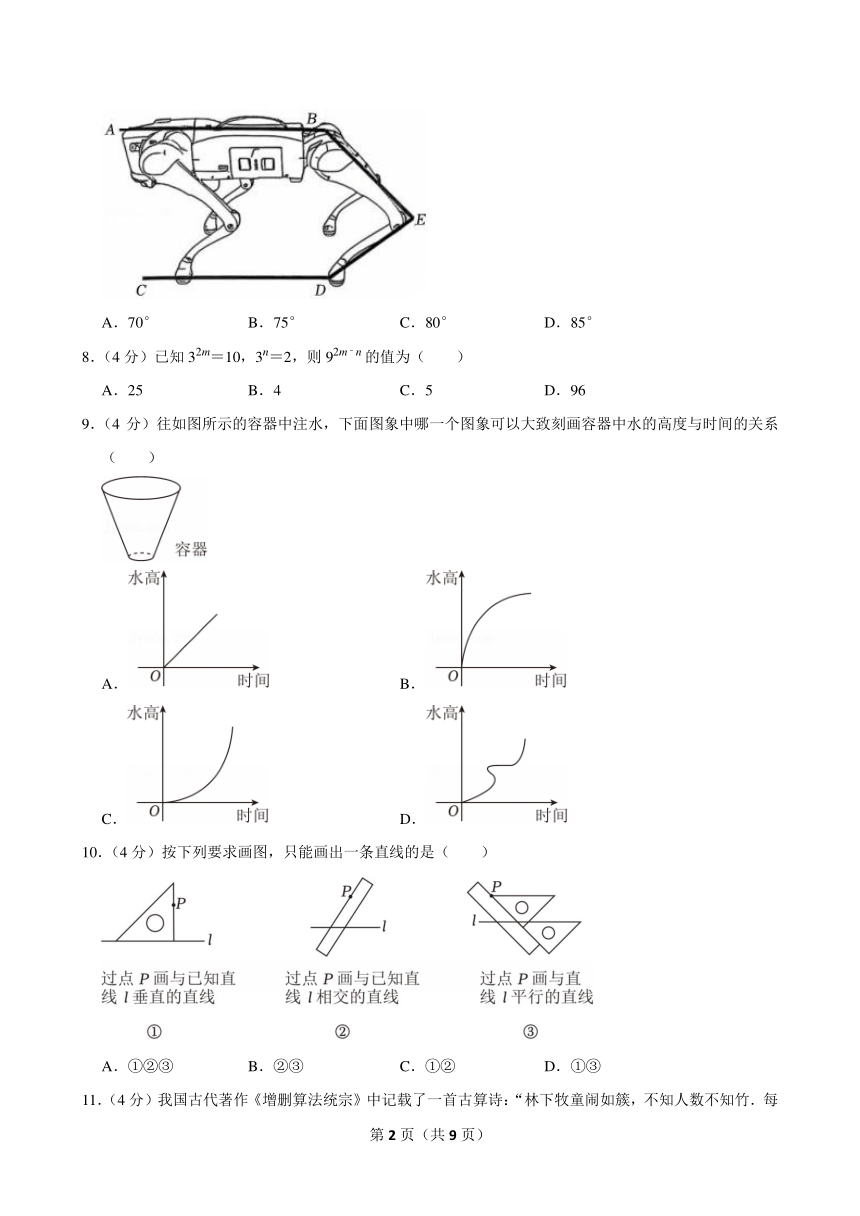
7.(4分)随着科技的进步和人工智能技术的成熟,仿生机器狗有望成为人们生活中的重要伙伴.如图所示,仿生机器狗平稳站立时,AB∥CD,∠ABE=135°,∠CDE=145°,此时∠BED的度数为( )
A.70° B.75° C.80° D.85°
8.(4分)已知32m=10,3n=2,则92m﹣n的值为( )
A.25 B.4 C.5 D.96
9.(4分)往如图所示的容器中注水,下面图象中哪一个图象可以大致刻画容器中水的高度与时间的关系( )
A. B.
C. D.
10.(4分)按下列要求画图,只能画出一条直线的是( )
A.①②③ B.②③ C.①② D.①③
11.(4分)我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹.每人六竿多十四,每人八竿恰齐足.”其大意是:牧童们在树下拿着竹竿高兴地玩耍,不知道有多少人和竹竿.每人6竿,多14竿;每人8竿,不多不少.下列说法正确的是( )
A.设牧童有x人,所列方程为6x﹣14=8x
B.设竹竿有y根,所列方程为
C.竹竿有28根
D.牧童有7人
12.(4分)如图,∠AOB=∠COD=∠EOF=90°,则∠1,∠2,∠3之间的数量关系为( )
A.∠1+∠2+∠3=90° B.∠1+∠2﹣∠3=90°
C.∠2+∠3﹣∠1=90° D.∠1﹣∠2+∠3=90°
二、填空题:本大题共10个小题,每小题4分,共40分。
13.(4分)计算: .
14.(4分)如图,将平面镜放置在桌面AB上,光线CO经过平面镜反射形成光线OD.已知EO⊥AB,∠AOC=35°,则∠DOE的度数为 .
15.(4分)若关于x的方程xm﹣1+2m+1=0是一元一次方程,则m的值是 .
16.(4分)如图,请你写出一个条件使得l1∥l2(不再标注其他字母或数字),你写的条件是 .
17.(4分)若x2﹣kx+25是一个完全平方式,则k= .
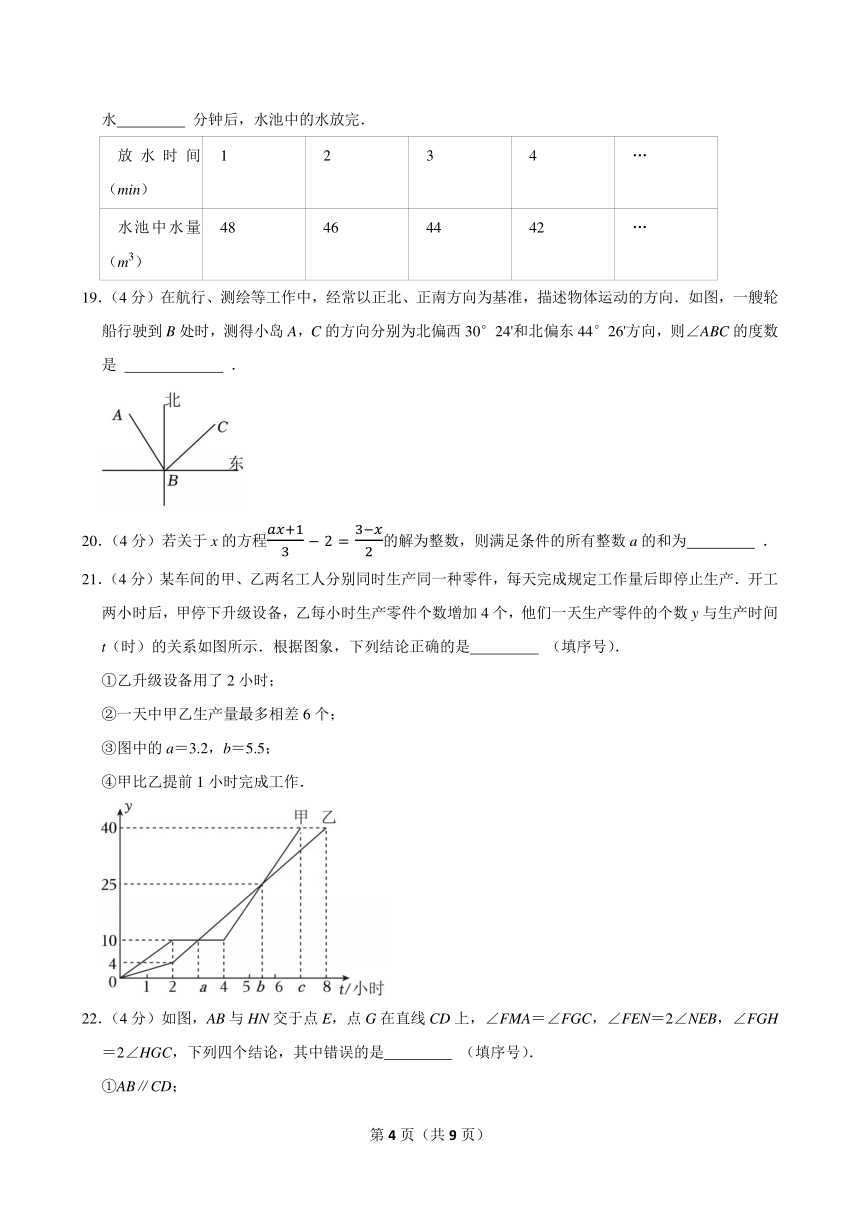
18.(4分)一个蓄水池有水50m3,打开放水闸门匀速放水,水池中的水量和放水时间的关系如表,则放水 分钟后,水池中的水放完.
放水时间(min) 1 2 3 4 …
水池中水量(m3) 48 46 44 42 …
19.(4分)在航行、测绘等工作中,经常以正北、正南方向为基准,描述物体运动的方向.如图,一艘轮船行驶到B处时,测得小岛A,C的方向分别为北偏西30°24'和北偏东44°26'方向,则∠ABC的度数是 .
20.(4分)若关于x的方程的解为整数,则满足条件的所有整数a的和为 .
21.(4分)某车间的甲、乙两名工人分别同时生产同一种零件,每天完成规定工作量后即停止生产.开工两小时后,甲停下升级设备,乙每小时生产零件个数增加4个,他们一天生产零件的个数y与生产时间t(时)的关系如图所示.根据图象,下列结论正确的是 (填序号).
①乙升级设备用了2小时;
②一天中甲乙生产量最多相差6个;
③图中的a=3.2,b=5.5;
④甲比乙提前1小时完成工作.
22.(4分)如图,AB与HN交于点E,点G在直线CD上,∠FMA=∠FGC,∠FEN=2∠NEB,∠FGH=2∠HGC,下列四个结论,其中错误的是 (填序号).
①AB∥CD;
②∠FEN+∠FGH=2∠EHG;
③∠EHG+∠EFM=90°;
④5∠EHG﹣∠EFM=180°.
三、解答题:本大题共7个小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
23.(8分)解方程:
(1)5x﹣6=3(x﹣4)+2;
(2).
24.(8分)先化简,再求值:(x+y)2+(x+y)(x﹣y),其中x=2,y=﹣1.
25.(8分)已知:如图,AD⊥BC,EG⊥BC,垂足分别为D,G,∠1=∠E.
求证:AD为∠BAC的平分线.
证明:因为AD⊥BC,EG⊥BC(已知),
所以∠ADC=∠EGC=90°(根据“ ”),
所以AD∥ (根据“ ”),
所以∠1=∠2(根据“ ”),
∠E= (根据“ ”),
又因为∠1=∠E(已知),
所以∠2=∠ (根据“ ”),
即AD为∠BAC的平分线.
26.(8分)某商场采购甲、乙两种篮球,采购40个甲种篮球和30个乙种篮球共需要5550元,其中甲、乙两种篮球的进价和售价如表:
甲种篮球 乙种篮球
进价(元/个) m m﹣25
售价(元/个) 100 75
(1)求表中m的值;
(2)第二次商场采购了35个甲种篮球和45个乙种篮球,由于两种篮球进价都比上次优惠了20%,商场准备对甲种篮球进行打折出售,让利于顾客,乙种篮球价格不变,全部售完后总利润为1665元,求甲种篮球打了几折?
27.(10分)在“看图说故事”数学学习活动中,某学习小组结合图象设计了一个问题情境.已知小明的家、超市、图书馆依次在同一条直线上,小明家离超市1.2km,超市离图书馆2km.小明从家出发,匀速步行到超市,在超市停留18分钟后,匀速步行到达图书馆,在图书馆停留了30min,然后骑行返回家.给出的图象反映了这个过程中小明离家的距离y km与离家的时间x min之间的对应关系.
请根据相关信息,解答下列问题:
(1)根据图中数据填写下表:
小明离家的时间/min 5 15 25 35 45 55 65 75 85
小明离家的距离/km
1.2
3.2 3.2
(2)求小明从超市到图书馆的步行速度和从图书馆到家得骑行速度.
28.(10分)【综合与实践】:【实践操作】三角尺中的数学:数学实践活动课上,学习小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
【问题发现】:
(1)①填空:如图1,若∠ACB=150°,则∠ACE的度数是 ,∠DCB的度数是 ,∠ECD的度数是 ;
②如图1,你发现∠ACE与∠DCB的大小有何关系?∠ACB与∠ECD的大小又有何关系?请直接写出你发现的结论;
【类比探究】:(2)如图2,当△ACD与△BCE与没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
29.(10分)如图1,点O在直线AB上,过点O引一条射线OC,使∠AOC=50°,将一个直角三角尺的直角顶点放在O点处,直角边OM在射线OB上,另一边ON在直线AB的下方.
【操作一】:将图1中的三角尺绕着点O以每秒20°的速度按顺时针方向旋转.当它完成旋转一周时停止,设旋转的时同为t秒.
(1)∠BOC的度数是 .
(2)①三角尺的边OM旋转的度数可表示为 (用含t的代数式表示);
②求t为何值时∠COM=90°.
【操作二】:如图2,射线OE与射线OC重合.如图3,在三角尺绕着点O以每秒20°的速度按顺时针方向旋转的同时,射线OE绕点O以每秒10°的速度按顺时针方向旋转,当三角板完成旋转一周时停止,射线OE也停止旋转,设旋转的时间为t秒.
(3)试探索:在三角尺与射线OE旋转的过程中,t为何值时,∠COE与∠COM中其中一个角是另一个角的两倍?请直接写出所有满足题意的t的值 .
2024-2025学年山东省淄博市博山区六年级(下)期末数学试卷(五四学制)
参考答案
一、选择题:本大题共12个小题,每小题4分,共48分。在每小题所给出的四个选项中,只有一项是符合题目要求的。
1.D; 2.D; 3.C; 4.B; 5.A; 6.B; 7.C; 8.A; 9.B; 10.D; 11.D; 12.D;
二、填空题:本大题共10个小题,每小题4分,共40分。
13.3 ; 14.55° ; 15.2 ; 16.∠1=∠2(答案不唯一) ; 17.±10 ; 18.25 ; 19.74°50′ ; 20.﹣6 ; 21.②④ ; 22.③④ ;
三、解答题:本大题共7个小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
23.(1)x=﹣2;
(2)x=﹣3. ; 24.2x2+2xy,4. ; 25.垂直的定义 ; EG ; 同位角相等,两直线平行 ; 两直线平行,内错角相等 ; ∠3 ; 两直线平行,同位角相等 ; 3 ; 等量代换 ; 26.(1)90;
(2)甲种篮球打了九折. ; 27.0.5 ; 1.2 ; 1.7 ; 2.7 ; 3.2 ; 1.6 ; 28.60° ; 60° ; 30° ; 29.130° ; 20°t ; 或或 ;
第1页(共1页)
一、选择题:本大题共12个小题,每小题4分,共48分。在每小题所给出的四个选项中,只有一项是符合题目要求的。
1.(4分)如图,下列给出的直线、射线和线段中能相交的是( )
A.a与b B.c与d C.b与d D.a与c
2.(4分)x=3是下列哪个方程的解( )
A.3x﹣1=2 B.2x﹣3=﹣x C.|x﹣3|=1 D.(x﹣1)2=4
3.(4分)如图,直线AB,CD相交于点O,若∠1=∠2=40°,则∠BOE的度数是( )
A.40° B.60° C.80° D.100°
4.(4分)用科学记数法表示的数3×10﹣3在数轴上的位置最接近( )
A.点P B.点Q C.点M D.点N
5.(4分)下列运算中,不正确的是( )
A.(﹣a3)2=a9 B.a3+a3=2a3 C.a2 a3=a5 D.2a3÷a2=2a
6.(4分)观察图1,若天平保持平衡,在图2天平的右盘中需放入( )个〇才能使其平衡.
A.5 B.6 C.7 D.8
7.(4分)随着科技的进步和人工智能技术的成熟,仿生机器狗有望成为人们生活中的重要伙伴.如图所示,仿生机器狗平稳站立时,AB∥CD,∠ABE=135°,∠CDE=145°,此时∠BED的度数为( )
A.70° B.75° C.80° D.85°
8.(4分)已知32m=10,3n=2,则92m﹣n的值为( )
A.25 B.4 C.5 D.96
9.(4分)往如图所示的容器中注水,下面图象中哪一个图象可以大致刻画容器中水的高度与时间的关系( )
A. B.
C. D.
10.(4分)按下列要求画图,只能画出一条直线的是( )
A.①②③ B.②③ C.①② D.①③
11.(4分)我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹.每人六竿多十四,每人八竿恰齐足.”其大意是:牧童们在树下拿着竹竿高兴地玩耍,不知道有多少人和竹竿.每人6竿,多14竿;每人8竿,不多不少.下列说法正确的是( )
A.设牧童有x人,所列方程为6x﹣14=8x
B.设竹竿有y根,所列方程为
C.竹竿有28根
D.牧童有7人
12.(4分)如图,∠AOB=∠COD=∠EOF=90°,则∠1,∠2,∠3之间的数量关系为( )
A.∠1+∠2+∠3=90° B.∠1+∠2﹣∠3=90°
C.∠2+∠3﹣∠1=90° D.∠1﹣∠2+∠3=90°
二、填空题:本大题共10个小题,每小题4分,共40分。
13.(4分)计算: .
14.(4分)如图,将平面镜放置在桌面AB上,光线CO经过平面镜反射形成光线OD.已知EO⊥AB,∠AOC=35°,则∠DOE的度数为 .
15.(4分)若关于x的方程xm﹣1+2m+1=0是一元一次方程,则m的值是 .
16.(4分)如图,请你写出一个条件使得l1∥l2(不再标注其他字母或数字),你写的条件是 .
17.(4分)若x2﹣kx+25是一个完全平方式,则k= .
18.(4分)一个蓄水池有水50m3,打开放水闸门匀速放水,水池中的水量和放水时间的关系如表,则放水 分钟后,水池中的水放完.
放水时间(min) 1 2 3 4 …
水池中水量(m3) 48 46 44 42 …
19.(4分)在航行、测绘等工作中,经常以正北、正南方向为基准,描述物体运动的方向.如图,一艘轮船行驶到B处时,测得小岛A,C的方向分别为北偏西30°24'和北偏东44°26'方向,则∠ABC的度数是 .
20.(4分)若关于x的方程的解为整数,则满足条件的所有整数a的和为 .
21.(4分)某车间的甲、乙两名工人分别同时生产同一种零件,每天完成规定工作量后即停止生产.开工两小时后,甲停下升级设备,乙每小时生产零件个数增加4个,他们一天生产零件的个数y与生产时间t(时)的关系如图所示.根据图象,下列结论正确的是 (填序号).
①乙升级设备用了2小时;
②一天中甲乙生产量最多相差6个;
③图中的a=3.2,b=5.5;
④甲比乙提前1小时完成工作.
22.(4分)如图,AB与HN交于点E,点G在直线CD上,∠FMA=∠FGC,∠FEN=2∠NEB,∠FGH=2∠HGC,下列四个结论,其中错误的是 (填序号).
①AB∥CD;
②∠FEN+∠FGH=2∠EHG;
③∠EHG+∠EFM=90°;
④5∠EHG﹣∠EFM=180°.
三、解答题:本大题共7个小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
23.(8分)解方程:
(1)5x﹣6=3(x﹣4)+2;
(2).
24.(8分)先化简,再求值:(x+y)2+(x+y)(x﹣y),其中x=2,y=﹣1.
25.(8分)已知:如图,AD⊥BC,EG⊥BC,垂足分别为D,G,∠1=∠E.
求证:AD为∠BAC的平分线.
证明:因为AD⊥BC,EG⊥BC(已知),
所以∠ADC=∠EGC=90°(根据“ ”),
所以AD∥ (根据“ ”),
所以∠1=∠2(根据“ ”),
∠E= (根据“ ”),
又因为∠1=∠E(已知),
所以∠2=∠ (根据“ ”),
即AD为∠BAC的平分线.
26.(8分)某商场采购甲、乙两种篮球,采购40个甲种篮球和30个乙种篮球共需要5550元,其中甲、乙两种篮球的进价和售价如表:
甲种篮球 乙种篮球
进价(元/个) m m﹣25
售价(元/个) 100 75
(1)求表中m的值;
(2)第二次商场采购了35个甲种篮球和45个乙种篮球,由于两种篮球进价都比上次优惠了20%,商场准备对甲种篮球进行打折出售,让利于顾客,乙种篮球价格不变,全部售完后总利润为1665元,求甲种篮球打了几折?
27.(10分)在“看图说故事”数学学习活动中,某学习小组结合图象设计了一个问题情境.已知小明的家、超市、图书馆依次在同一条直线上,小明家离超市1.2km,超市离图书馆2km.小明从家出发,匀速步行到超市,在超市停留18分钟后,匀速步行到达图书馆,在图书馆停留了30min,然后骑行返回家.给出的图象反映了这个过程中小明离家的距离y km与离家的时间x min之间的对应关系.
请根据相关信息,解答下列问题:
(1)根据图中数据填写下表:
小明离家的时间/min 5 15 25 35 45 55 65 75 85
小明离家的距离/km
1.2
3.2 3.2
(2)求小明从超市到图书馆的步行速度和从图书馆到家得骑行速度.
28.(10分)【综合与实践】:【实践操作】三角尺中的数学:数学实践活动课上,学习小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
【问题发现】:
(1)①填空:如图1,若∠ACB=150°,则∠ACE的度数是 ,∠DCB的度数是 ,∠ECD的度数是 ;
②如图1,你发现∠ACE与∠DCB的大小有何关系?∠ACB与∠ECD的大小又有何关系?请直接写出你发现的结论;
【类比探究】:(2)如图2,当△ACD与△BCE与没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
29.(10分)如图1,点O在直线AB上,过点O引一条射线OC,使∠AOC=50°,将一个直角三角尺的直角顶点放在O点处,直角边OM在射线OB上,另一边ON在直线AB的下方.
【操作一】:将图1中的三角尺绕着点O以每秒20°的速度按顺时针方向旋转.当它完成旋转一周时停止,设旋转的时同为t秒.
(1)∠BOC的度数是 .
(2)①三角尺的边OM旋转的度数可表示为 (用含t的代数式表示);
②求t为何值时∠COM=90°.
【操作二】:如图2,射线OE与射线OC重合.如图3,在三角尺绕着点O以每秒20°的速度按顺时针方向旋转的同时,射线OE绕点O以每秒10°的速度按顺时针方向旋转,当三角板完成旋转一周时停止,射线OE也停止旋转,设旋转的时间为t秒.
(3)试探索:在三角尺与射线OE旋转的过程中,t为何值时,∠COE与∠COM中其中一个角是另一个角的两倍?请直接写出所有满足题意的t的值 .
2024-2025学年山东省淄博市博山区六年级(下)期末数学试卷(五四学制)
参考答案
一、选择题:本大题共12个小题,每小题4分,共48分。在每小题所给出的四个选项中,只有一项是符合题目要求的。
1.D; 2.D; 3.C; 4.B; 5.A; 6.B; 7.C; 8.A; 9.B; 10.D; 11.D; 12.D;
二、填空题:本大题共10个小题,每小题4分,共40分。
13.3 ; 14.55° ; 15.2 ; 16.∠1=∠2(答案不唯一) ; 17.±10 ; 18.25 ; 19.74°50′ ; 20.﹣6 ; 21.②④ ; 22.③④ ;
三、解答题:本大题共7个小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
23.(1)x=﹣2;
(2)x=﹣3. ; 24.2x2+2xy,4. ; 25.垂直的定义 ; EG ; 同位角相等,两直线平行 ; 两直线平行,内错角相等 ; ∠3 ; 两直线平行,同位角相等 ; 3 ; 等量代换 ; 26.(1)90;
(2)甲种篮球打了九折. ; 27.0.5 ; 1.2 ; 1.7 ; 2.7 ; 3.2 ; 1.6 ; 28.60° ; 60° ; 30° ; 29.130° ; 20°t ; 或或 ;
第1页(共1页)
同课章节目录
