2024-2025学年甘肃省平凉市庄浪县九年级(下)第一次月考数学试卷(含简单答案)
文档属性
| 名称 | 2024-2025学年甘肃省平凉市庄浪县九年级(下)第一次月考数学试卷(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 00:00:00 | ||
图片预览



文档简介
2024-2025学年甘肃省平凉市庄浪县九年级(下)第一次月考数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.一种化肥的包装袋上标着净重(40±0.2)kg,那么两袋这种化肥质量的差不可能是( )
A. 0.42kg B. 0kg C. 0.15kg D. 0.38kg
2.如图,点C在线段AB上,下列说法正确的是( )
A. AC=BC-AB B. AB=2AC C. AC=BC D. AB=AC+CB
3.下列运算正确的是( )
A. a5-a3=a2 B. 2a2+a3=2a5 C. (-3a2)2=9a4 D. a6÷a2=a3
4.如图,是由若干个相同的小正方体组成的几何体,该几何体的俯视图,主视图,左视图的面积分别为S1,S2,S3.下列说法正确的是( )
A. S1=S2>S3
B. S1>S2=S3
C. S3>S1=S2
D. S1=S2=S3
5.农历八月十五是中国的中秋节,在这一天吃月饼成为千百年来中华民族的传统,寓意为月圆人团圆.亮亮随机称量了家里的几个月饼,它们的质量(单位:克)分别是:100.4,100.4,99.6,100.2,99.5,99.4,这几个数据的中位数和众数分别是( )
A. 100.4,100.4 B. 100.4,99.2 C. 99.9,100.4 D. 99.6,100.4
6.若关于x的一元二次方程x2-2x+k=0有两个不相等的实数根,则k的取值范围为( )
A. k≥1 B. k>1 C. k≤1 D. k<1
7.如图,在扇形OAB中,有矩形OCDE和矩形OFGH,点D、G在上,点C、F在OA上,点E、H在OB上,对角线HF和CE的长分别为a,b,则下列说法正确的是( )
A. 不能确定
B. a>b
C. a<b
D. a=b
8.已知M=9a 9a 9a,N=,若M=3N,则下列式子成立的是( )
A. 6a=k+2 B. 9a=k+3 C. 2a=9k D. 6a=k+3
9.静静一家计划外出旅游,家中的一盆海棠无人照料,为此静静从网上买来了一个简易滴水装置,既可以通过调节水滴流速控制每天的浇水量又可以节水.通过实验静静得到了如图所示的天数y(天)与每天用水量x(百滴)之间的函数关系.已知,这盆海棠生长阶段过程中需要浇水量为每天400~500滴,利用此装置,最少可以用的天数为( )
A. 18天 B. 19天 C. 20天 D. 21天
10.老师在黑板上给出了一道分式计算题:.
沙沙解答过程:
=…①
=…②
=…③
…
沙沙的解答过程是从______开始出现错误的,正确的结果是______,下列结论正确的是( )
A. ①, B. ②, C. ②, D. ①,
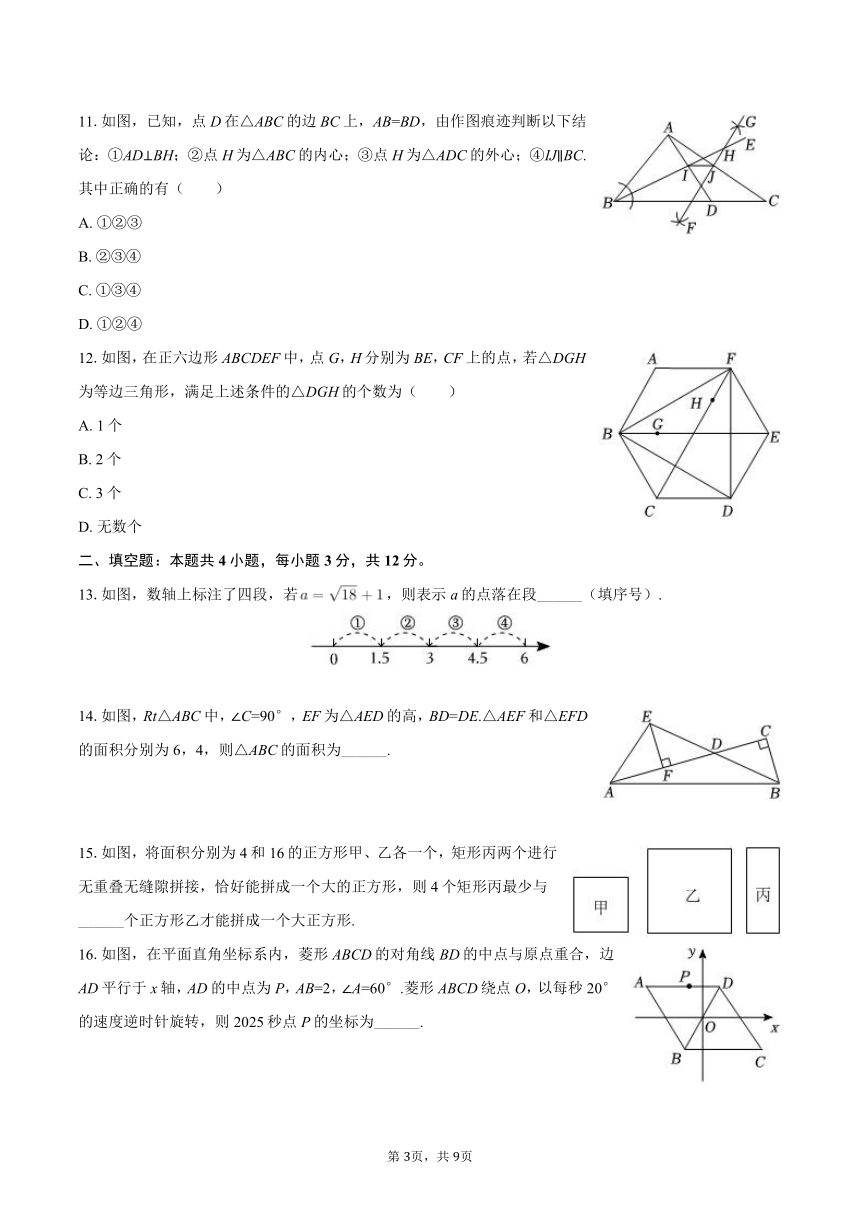
11.如图,已知,点D在△ABC的边BC上,AB=BD,由作图痕迹判断以下结论:①AD⊥BH;②点H为△ABC的内心;③点H为△ADC的外心;④IJ∥BC.其中正确的有( )
A. ①②③
B. ②③④
C. ①③④
D. ①②④
12.如图,在正六边形ABCDEF中,点G,H分别为BE,CF上的点,若△DGH为等边三角形,满足上述条件的△DGH的个数为( )
A. 1个
B. 2个
C. 3个
D. 无数个
二、填空题:本题共4小题,每小题3分,共12分。
13.如图,数轴上标注了四段,若,则表示a的点落在段______(填序号).
14.如图,Rt△ABC中,∠C=90°,EF为△AED的高,BD=DE.△AEF和△EFD的面积分别为6,4,则△ABC的面积为______.
15.如图,将面积分别为4和16的正方形甲、乙各一个,矩形丙两个进行无重叠无缝隙拼接,恰好能拼成一个大的正方形,则4个矩形丙最少与______个正方形乙才能拼成一个大正方形.
16.如图,在平面直角坐标系内,菱形ABCD的对角线BD的中点与原点重合,边AD平行于x轴,AD的中点为P,AB=2,∠A=60°.菱形ABCD绕点O,以每秒20°的速度逆时针旋转,则2025秒点P的坐标为______.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
五角星是我国国旗的重要组成元素,课堂上静静突发奇想,利用五角星编制了一个数学循环运算程序,如图,点A为输入端,点B的运算为加上原数的2倍,点C的运算为乘(-1),点D的运算为乘,点E的运算为乘100.运算规则为:A-B-C-D-E-A- .其中A-B-C-D-E为一个运算周期.
(1)若输入的数字为3,计算一个运算周期后的运算结果;
(2)若输入的数字为-2,用科学记数法表示五个运算周期后的运算结果.
18.(本小题8分)
课堂上老师规定了一种运算:.如:.
(1)若.求x的取值范围;
(2)红红说的运算结果不可能大于15.红红的说法是否正确,请说明理由.
19.(本小题8分)
随着科技的进步.人工智能得到了巨大的发展.如图是一款机械臂机器人.基座AB与地面垂直,基座AB=米.大臂BC=2米.小臂CD=3米.大臂与水平线的张角为α,小臂与大臂的张角为β,其中30°≤α≤60°,15°≤β≤90°.(图中点线在同一个平面内)
(1)求机械臂机器人抓手D距离地面的最大高度;(精确到0.1米)
(2)设抓手D到直线AB的水平距离为r,当∠α=60°时,求r的取值范围.(精确到0.1米)(参考数据:≈1.4)
20.(本小题8分)
一个大型多肉花卉生产基地,培育了2万株多肉花卉.为了估计这批花卉的产值,对这批多肉花冠的直径进行了抽样调查;并绘制了如图不完整的统计图.已知多肉A,B,C,D的销售单价分别为:25元,28元,30元,35元.
项目
型号 花冠直径x(cm) 频数 频率
A x<22 50 10%
B 22≤x<25 a 28%
C 25≤x<28 260 b
D x>28 50 10%
(1)求出a,b的值,并补全统计图;
(2)估计这批多肉花卉的产值为多少万元;
(3)一个纸箱内有包装好的4盆多肉(包装外观完全相同),分别装有一盆红色花边多肉,2盆黄色花边多肉,1盆粉色花边多肉,任意取出2盆,求刚好是红色花边,粉色花边多肉各一盆的概率.
21.(本小题8分)
如图,在平面直角坐标系内,将点C(1,1)向上平移3个单位长度得到点A.将点C(1,1)向右平移3个单位长度得到点B,连接AC,BC,作直线AB.直线y=x+b是直线y=x-4沿y轴以每秒1个单位长度的速度向上平移t秒得到的,直线y=x+b与y轴交于点F.
(1)求直线AB的解析式;
(2)若△ABF的周长最小,求t的值;
(3)直接写出t为何值时,△ABC的面积被直线y=x+b分为1:2两部分.
22.(本小题8分)
“豆腐石磨”是我国古人制作豆腐的重要的生产工具,更是劳动人民智慧的结晶.生产过程中它主要靠人力推动木柄AC,带动上方石磨转动(下方石磨不动),将豆粒磨碎,进行生产.它的主要工作部件可以看成一个圆和线段,俯视图如图②所示.如图③,O为石磨的圆心,连接OA.已知OA与石磨的边缘交于点D,木柄AC=1.2米,连接BD,OB,O、B、C三点共线,A始终在OE上运动,⊙O的半径OB=0.3米,固定点C到石磨边缘距离BC=0.1米.
(1)在同等条件下,OC⊥AC时,工作最省力,求此时∠A的正切值;
(2)在石磨转动过程中,求DA的取值范围;
(3)在工作的过程中,线段BD能否与AC平行,请说明理由.
23.(本小题8分)
消防员在一款软件中进行模拟灭火.如图,OB为2米高的围墙,围墙内有一坡度为i=的斜坡OC,水流路线L为抛物线的一部分,点A为消防车出水口,出水口距离地面2米,距离围墙5米,建立如图所示的平面直角坐标系,抛物线的解析式为y=-+bx+c(b,c为常数).
(1)若水流恰好经过围墙OB的顶端,求抛物线的解析式;
(2)在(1)的条件下,求斜坡上水流点E到围墙的距离;
(3)着火点F位于斜坡上,且点F到点O,B的距离相等,设抛物线与y轴交于点H.
①若消防车向围墙前进了2米,水流刚好到达着火点F,求HB的长;
②若消防车喷水的最大高度为m米,为了保证灭火效果,喷水点需要到达F上方4米的G点,直接写出m的最小值,并直接写出此时消防车向前移动的距离.
24.(本小题8分)
如图①,已知,Rt△ABC中,∠ABC=90°,AB=6,BC=8.点D为线段AC上一动点.连接BD,将△BCD沿BD折叠,得到△BC′D,连接CC′,BD或BD的延长线交CC′于点E.
(1)说明线段BE和线段CC′的位置关系;
(2)当A,C′,C共线时,求线段AC′,线段CD的长;
(3)①点D为AC中点时,求△C′DE的面积;
②若点E位于AB的中垂线上,求点E到AB的距离.
(4)如图②,若C′D交AB于点F,直接写出AF的最大值.
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】C
12.【答案】D
13.【答案】④
14.【答案】14
15.【答案】2
16.【答案】(,)
17.【答案】-300;
2×1010.
18.【答案】x<1; 红红的说法正确,理由见解答.
19.【答案】5.2米;
1.1米≤r≤2.0米.
20.【答案】a=140,b=52%;
58.88万元;
.
21.【答案】y=-x+5;
;
或秒.
22.【答案】;
0.5米≤AD≤1.3米;
线段BD不能与AC平行;见解析.
23.【答案】;
米;
①米;
②m的最小值为5,消防车向前移动的距离为米.
24.【答案】BE⊥CC′.
;.
①;②+4.
.
第1页,共1页
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.一种化肥的包装袋上标着净重(40±0.2)kg,那么两袋这种化肥质量的差不可能是( )
A. 0.42kg B. 0kg C. 0.15kg D. 0.38kg
2.如图,点C在线段AB上,下列说法正确的是( )
A. AC=BC-AB B. AB=2AC C. AC=BC D. AB=AC+CB
3.下列运算正确的是( )
A. a5-a3=a2 B. 2a2+a3=2a5 C. (-3a2)2=9a4 D. a6÷a2=a3
4.如图,是由若干个相同的小正方体组成的几何体,该几何体的俯视图,主视图,左视图的面积分别为S1,S2,S3.下列说法正确的是( )
A. S1=S2>S3
B. S1>S2=S3
C. S3>S1=S2
D. S1=S2=S3
5.农历八月十五是中国的中秋节,在这一天吃月饼成为千百年来中华民族的传统,寓意为月圆人团圆.亮亮随机称量了家里的几个月饼,它们的质量(单位:克)分别是:100.4,100.4,99.6,100.2,99.5,99.4,这几个数据的中位数和众数分别是( )
A. 100.4,100.4 B. 100.4,99.2 C. 99.9,100.4 D. 99.6,100.4
6.若关于x的一元二次方程x2-2x+k=0有两个不相等的实数根,则k的取值范围为( )
A. k≥1 B. k>1 C. k≤1 D. k<1
7.如图,在扇形OAB中,有矩形OCDE和矩形OFGH,点D、G在上,点C、F在OA上,点E、H在OB上,对角线HF和CE的长分别为a,b,则下列说法正确的是( )
A. 不能确定
B. a>b
C. a<b
D. a=b
8.已知M=9a 9a 9a,N=,若M=3N,则下列式子成立的是( )
A. 6a=k+2 B. 9a=k+3 C. 2a=9k D. 6a=k+3
9.静静一家计划外出旅游,家中的一盆海棠无人照料,为此静静从网上买来了一个简易滴水装置,既可以通过调节水滴流速控制每天的浇水量又可以节水.通过实验静静得到了如图所示的天数y(天)与每天用水量x(百滴)之间的函数关系.已知,这盆海棠生长阶段过程中需要浇水量为每天400~500滴,利用此装置,最少可以用的天数为( )
A. 18天 B. 19天 C. 20天 D. 21天
10.老师在黑板上给出了一道分式计算题:.
沙沙解答过程:
=…①
=…②
=…③
…
沙沙的解答过程是从______开始出现错误的,正确的结果是______,下列结论正确的是( )
A. ①, B. ②, C. ②, D. ①,
11.如图,已知,点D在△ABC的边BC上,AB=BD,由作图痕迹判断以下结论:①AD⊥BH;②点H为△ABC的内心;③点H为△ADC的外心;④IJ∥BC.其中正确的有( )
A. ①②③
B. ②③④
C. ①③④
D. ①②④
12.如图,在正六边形ABCDEF中,点G,H分别为BE,CF上的点,若△DGH为等边三角形,满足上述条件的△DGH的个数为( )
A. 1个
B. 2个
C. 3个
D. 无数个
二、填空题:本题共4小题,每小题3分,共12分。
13.如图,数轴上标注了四段,若,则表示a的点落在段______(填序号).
14.如图,Rt△ABC中,∠C=90°,EF为△AED的高,BD=DE.△AEF和△EFD的面积分别为6,4,则△ABC的面积为______.
15.如图,将面积分别为4和16的正方形甲、乙各一个,矩形丙两个进行无重叠无缝隙拼接,恰好能拼成一个大的正方形,则4个矩形丙最少与______个正方形乙才能拼成一个大正方形.
16.如图,在平面直角坐标系内,菱形ABCD的对角线BD的中点与原点重合,边AD平行于x轴,AD的中点为P,AB=2,∠A=60°.菱形ABCD绕点O,以每秒20°的速度逆时针旋转,则2025秒点P的坐标为______.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
五角星是我国国旗的重要组成元素,课堂上静静突发奇想,利用五角星编制了一个数学循环运算程序,如图,点A为输入端,点B的运算为加上原数的2倍,点C的运算为乘(-1),点D的运算为乘,点E的运算为乘100.运算规则为:A-B-C-D-E-A- .其中A-B-C-D-E为一个运算周期.
(1)若输入的数字为3,计算一个运算周期后的运算结果;
(2)若输入的数字为-2,用科学记数法表示五个运算周期后的运算结果.
18.(本小题8分)
课堂上老师规定了一种运算:.如:.
(1)若.求x的取值范围;
(2)红红说的运算结果不可能大于15.红红的说法是否正确,请说明理由.
19.(本小题8分)
随着科技的进步.人工智能得到了巨大的发展.如图是一款机械臂机器人.基座AB与地面垂直,基座AB=米.大臂BC=2米.小臂CD=3米.大臂与水平线的张角为α,小臂与大臂的张角为β,其中30°≤α≤60°,15°≤β≤90°.(图中点线在同一个平面内)
(1)求机械臂机器人抓手D距离地面的最大高度;(精确到0.1米)
(2)设抓手D到直线AB的水平距离为r,当∠α=60°时,求r的取值范围.(精确到0.1米)(参考数据:≈1.4)
20.(本小题8分)
一个大型多肉花卉生产基地,培育了2万株多肉花卉.为了估计这批花卉的产值,对这批多肉花冠的直径进行了抽样调查;并绘制了如图不完整的统计图.已知多肉A,B,C,D的销售单价分别为:25元,28元,30元,35元.
项目
型号 花冠直径x(cm) 频数 频率
A x<22 50 10%
B 22≤x<25 a 28%
C 25≤x<28 260 b
D x>28 50 10%
(1)求出a,b的值,并补全统计图;
(2)估计这批多肉花卉的产值为多少万元;
(3)一个纸箱内有包装好的4盆多肉(包装外观完全相同),分别装有一盆红色花边多肉,2盆黄色花边多肉,1盆粉色花边多肉,任意取出2盆,求刚好是红色花边,粉色花边多肉各一盆的概率.
21.(本小题8分)
如图,在平面直角坐标系内,将点C(1,1)向上平移3个单位长度得到点A.将点C(1,1)向右平移3个单位长度得到点B,连接AC,BC,作直线AB.直线y=x+b是直线y=x-4沿y轴以每秒1个单位长度的速度向上平移t秒得到的,直线y=x+b与y轴交于点F.
(1)求直线AB的解析式;
(2)若△ABF的周长最小,求t的值;
(3)直接写出t为何值时,△ABC的面积被直线y=x+b分为1:2两部分.
22.(本小题8分)
“豆腐石磨”是我国古人制作豆腐的重要的生产工具,更是劳动人民智慧的结晶.生产过程中它主要靠人力推动木柄AC,带动上方石磨转动(下方石磨不动),将豆粒磨碎,进行生产.它的主要工作部件可以看成一个圆和线段,俯视图如图②所示.如图③,O为石磨的圆心,连接OA.已知OA与石磨的边缘交于点D,木柄AC=1.2米,连接BD,OB,O、B、C三点共线,A始终在OE上运动,⊙O的半径OB=0.3米,固定点C到石磨边缘距离BC=0.1米.
(1)在同等条件下,OC⊥AC时,工作最省力,求此时∠A的正切值;
(2)在石磨转动过程中,求DA的取值范围;
(3)在工作的过程中,线段BD能否与AC平行,请说明理由.
23.(本小题8分)
消防员在一款软件中进行模拟灭火.如图,OB为2米高的围墙,围墙内有一坡度为i=的斜坡OC,水流路线L为抛物线的一部分,点A为消防车出水口,出水口距离地面2米,距离围墙5米,建立如图所示的平面直角坐标系,抛物线的解析式为y=-+bx+c(b,c为常数).
(1)若水流恰好经过围墙OB的顶端,求抛物线的解析式;
(2)在(1)的条件下,求斜坡上水流点E到围墙的距离;
(3)着火点F位于斜坡上,且点F到点O,B的距离相等,设抛物线与y轴交于点H.
①若消防车向围墙前进了2米,水流刚好到达着火点F,求HB的长;
②若消防车喷水的最大高度为m米,为了保证灭火效果,喷水点需要到达F上方4米的G点,直接写出m的最小值,并直接写出此时消防车向前移动的距离.
24.(本小题8分)
如图①,已知,Rt△ABC中,∠ABC=90°,AB=6,BC=8.点D为线段AC上一动点.连接BD,将△BCD沿BD折叠,得到△BC′D,连接CC′,BD或BD的延长线交CC′于点E.
(1)说明线段BE和线段CC′的位置关系;
(2)当A,C′,C共线时,求线段AC′,线段CD的长;
(3)①点D为AC中点时,求△C′DE的面积;
②若点E位于AB的中垂线上,求点E到AB的距离.
(4)如图②,若C′D交AB于点F,直接写出AF的最大值.
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】C
12.【答案】D
13.【答案】④
14.【答案】14
15.【答案】2
16.【答案】(,)
17.【答案】-300;
2×1010.
18.【答案】x<1; 红红的说法正确,理由见解答.
19.【答案】5.2米;
1.1米≤r≤2.0米.
20.【答案】a=140,b=52%;
58.88万元;
.
21.【答案】y=-x+5;
;
或秒.
22.【答案】;
0.5米≤AD≤1.3米;
线段BD不能与AC平行;见解析.
23.【答案】;
米;
①米;
②m的最小值为5,消防车向前移动的距离为米.
24.【答案】BE⊥CC′.
;.
①;②+4.
.
第1页,共1页
同课章节目录
