第五单元平行四边形和梯形同步练习(含解析)人教版数学四年级上册
文档属性
| 名称 | 第五单元平行四边形和梯形同步练习(含解析)人教版数学四年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 323.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 20:23:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五单元平行四边形和梯形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.把一张长方形纸连续对折两次后展开,三条折痕( )。
A.互相平行 B.互相垂直 C.相交 D.可能互相平行,也可能互相垂直
2.把一张长方形纸向同一个方向连续对折两次,形成的折痕的位置关系是( )。
A.互相平行 B.互相垂直 C.互相平行或互相垂直
3.下面( )组两直线相互垂直。
A. B. C. D.
4.过直线外一点画已知直线的垂线,可以画( )条。
A.1 B.2 C.无数
5.一个等腰梯形的上、下底之和是26厘米,周长是40厘米,则这个等腰梯形的一条腰长是( )厘米。
A.14 B.13 C.8 D.7
6.如图,三只小鸡同时发现了一条害虫,于是以同样的速度向害虫跑过去:( )最先吃到害虫。
A.小鸡1 B.小鸡2 C.小鸡3
7.捏住平行四边形的两个对角,向相反方向拉,它的周长( )。
A.不变 B.变短 C.变长 D.无法判断
8.下列图形中所作的高正确的是( )。
A. B. C. D.
9.从直线外一点画已知直线的平行线,可以画( )条。
A.1 B.2 C.3 D.无数条
10.下列说法中正确的是( )。
A.梯形是一种特殊的平行四边形
B.在梯形中,平行的一组对边叫作梯形的腰
C.直角梯形有无数条高
D.只有一组对边平行的图形都是梯形
二、填空题
11.在同一个平面内( )的两条直线叫作平行线,也可以说这两条直线( )。如果两条直线相交成直角,就说这两条直线( ),其中一条直线叫作另一条直线的( ),这两条直线的交点叫作( )。
12.数一数,如图中有( )个平行四边形,有( )个梯形。
13.丽丽在图中的平行四边形的A点出发画了两条高,BC边上的高是( )厘米。平行四边形具有( )的特性,伸缩门就是利用这种特性制作。
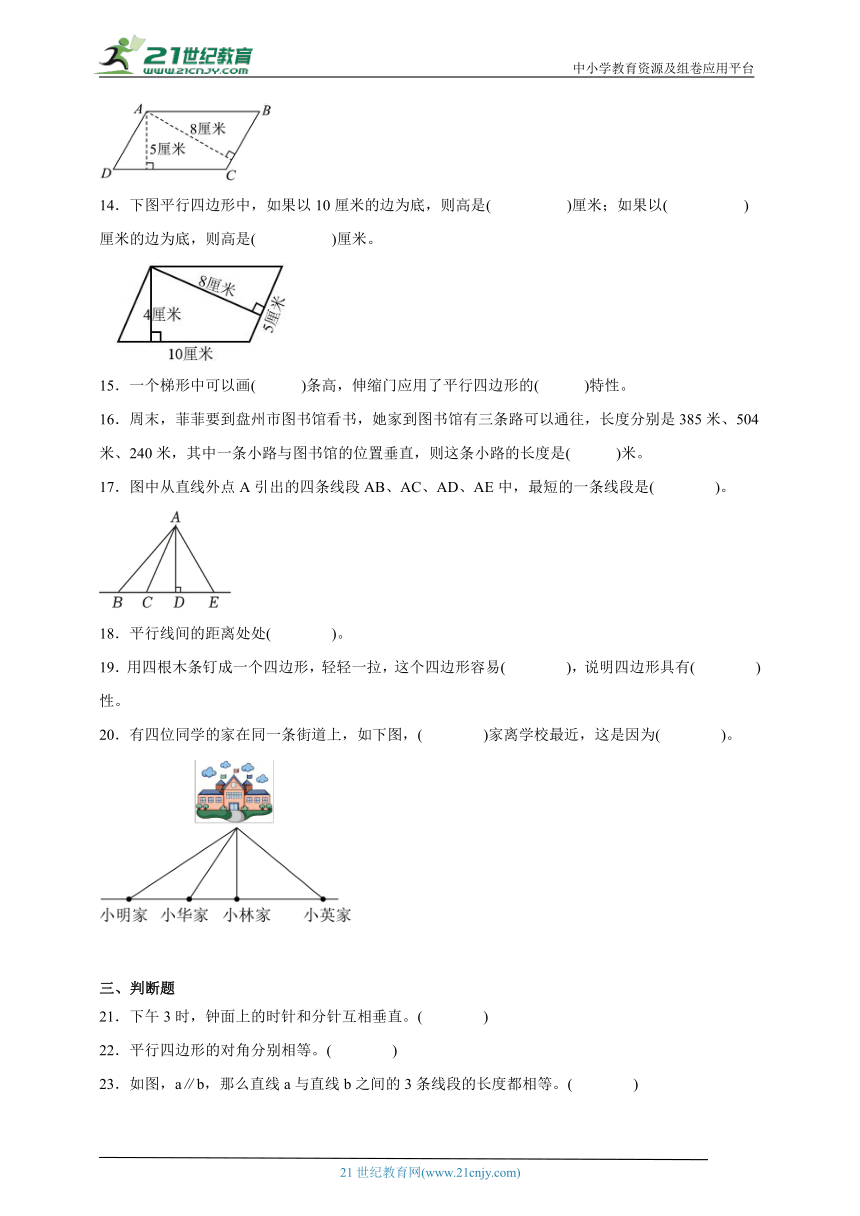
14.下图平行四边形中,如果以10厘米的边为底,则高是( )厘米;如果以( )厘米的边为底,则高是( )厘米。
15.一个梯形中可以画( )条高,伸缩门应用了平行四边形的( )特性。
16.周末,菲菲要到盘州市图书馆看书,她家到图书馆有三条路可以通往,长度分别是385米、504米、240米,其中一条小路与图书馆的位置垂直,则这条小路的长度是( )米。
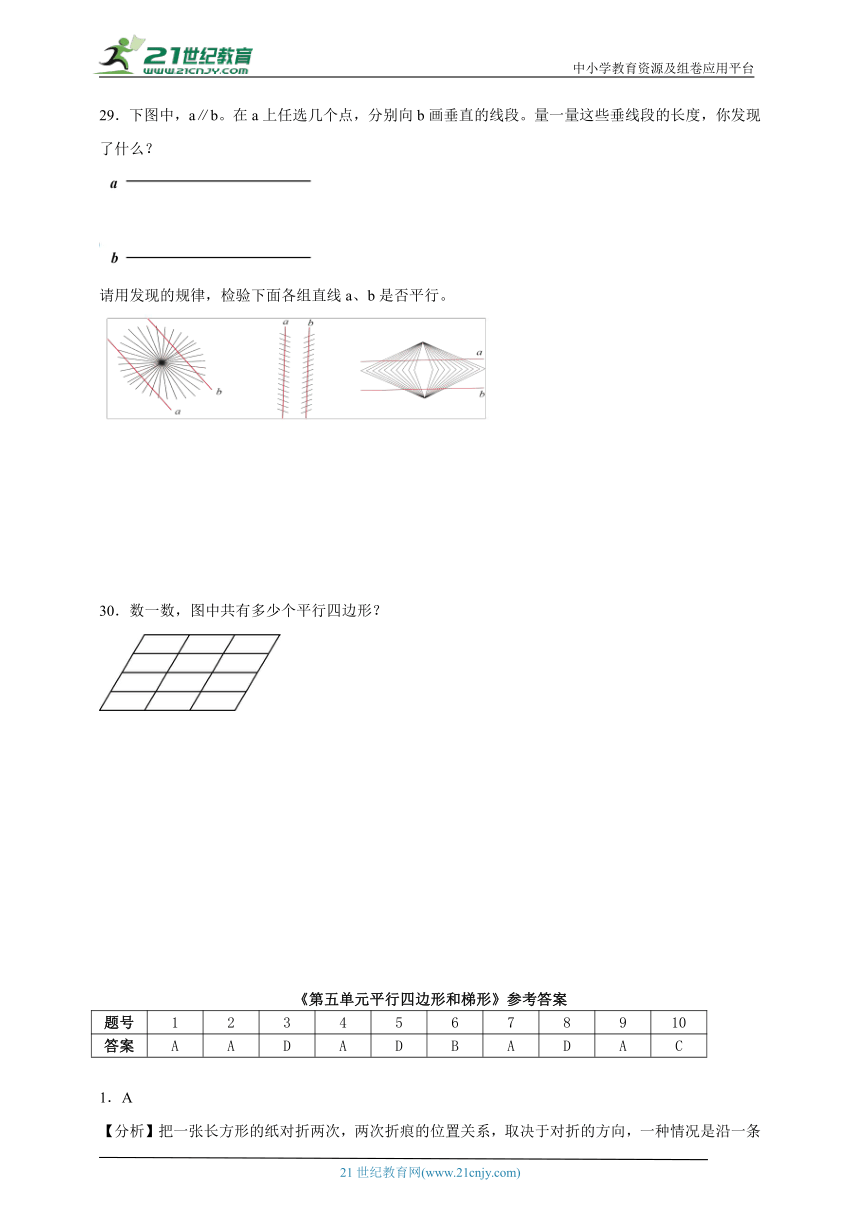
17.图中从直线外点A引出的四条线段AB、AC、AD、AE中,最短的一条线段是( )。
18.平行线间的距离处处( )。
19.用四根木条钉成一个四边形,轻轻一拉,这个四边形容易( ),说明四边形具有( )性。
20.有四位同学的家在同一条街道上,如下图,( )家离学校最近,这是因为( )。
三、判断题
21.下午3时,钟面上的时针和分针互相垂直。( )
22.平行四边形的对角分别相等。( )
23.如图,a∥b,那么直线a与直线b之间的3条线段的长度都相等。( )
24.同一平面内,任意一条直线的垂线有无数条。( )
25.过直线外一点画已知直线的平行线,可以画无数条。( )
四、解答题
26.量出下图中四个角的度数,并说说你有什么发现。
∠1=( ),∠2=( ),∠3=( ),∠4=( )。
我发现:
27.公园里有一个花坛的形状是平行四边形,它的周长是38米,其中一条边长为4米,其余三条边的长分别是多少米?
28.直线、射线和线段有什么联系和区别?同一平面内的两条直线有哪几种位置关系?
29.下图中,a∥b。在a上任选几个点,分别向b画垂直的线段。量一量这些垂线段的长度,你发现了什么?
请用发现的规律,检验下面各组直线a、b是否平行。
30.数一数,图中共有多少个平行四边形?
《第五单元平行四边形和梯形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D A D B A D A C
1.A
【分析】把一张长方形的纸对折两次,两次折痕的位置关系,取决于对折的方向,一种情况是沿一条边的同一个方向对折两次,三条折痕是互相平行的;另一种情况是沿两条边的两个方向对折,两条折痕的互相垂直的;由此得出结论。
【详解】一张长方形纸沿一个方向连续对折两次后展开,三条折痕互相平行。
故答案为:A
【点睛】解答本题的关键在于要从不同的折叠方形考虑,具体操作一下会更简捷。
2.A
【分析】同一平面内两条直线的位置关系:在同一平面内的两条不重合的直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况;平行的概念:同一平面内不相交的两条直线互相平行,其中一条直线是另一条直线的平行线;垂直的概念:两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线;据此解答。
【详解】根据分析如图:
把一张长方形纸向同一个方向连续对折两次,形成的折痕的位置关系是互相平行。
故答案为:A
3.D
【分析】在同一个平面内,不相交的两条直线叫做平行线,两条直线相交成直角时,就说这两条直线互相垂直,那么其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足;由此求解。
【详解】
A.两直线不互相平行,也不互相垂直;
B.两直线相交,但不互相垂直;
C.两直线互相平行;
D.两直线相互垂直。
故答案为:D
【点睛】解决本题关键是熟练掌握平行和垂直的定义。
4.A
【分析】过直线上或直线外一点作作垂线的步骤:把三角尺的一条直角边与已知直线重合,沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上,沿三角尺的另一条直角边画一条直线,并画上垂直符号,这条直线就是已知直线的垂线。
【详解】通过分析可知:过直线外一点画已知直线的垂线可以画1条,过直线上一点画已知直线的垂线可以画1条。
故答案为:A
5.D
【分析】等腰梯形的两腰相等,这个梯形的周长减去上下底之和,再除以2即可算出它的一条腰长几厘米。
【详解】(40-26)÷2
=14÷2
=7(厘米)
则这个等腰梯形的一条腰长是7厘米。
故答案为:D
6.B
【分析】根据直线外一点到直线上各点的连线中,垂线段最短可知,小鸡2到害虫的距离最短,三只小鸡以同样的速度向害虫跑过去,小鸡2最先到达害虫位置,所以小鸡2最先吃到害虫,据此即可解答。
【详解】根据分析可知,三只小鸡同时发现了一条害虫,于是以同样的速度向害虫跑过去:小鸡2最先吃到害虫。
故答案为:B
7.A
【分析】平行四边形一旦确定,其四条边的长度也就确定了,由于平行四边形具有不稳定的特征,故其可以伸缩,但是无论怎么伸缩,其边的长度不变,据此解答即可。
【详解】捏住平行四边形的两个对角,向相反方向拉,虽然图形的形状变了,其边的长度不变,则其周长也不会发生改变。
故答案选:A
8.D
【分析】从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。
从三角形任一顶点向它的对边或者对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高。
从平行四边形的一条边上的任意一点都可以向对边作垂直线段,即是平行四边形的高。
【详解】A.不是从一条底边到它对边的垂直线段,不是梯形的高;
B.不是从顶点向它的对边的垂直线段,不是三角形的高;
C.不是垂直线段,不是平行四边形的高;
D.是从顶点到它的对边的垂直线段,是三角形的高。
故答案为:D
9.A
【分析】根据平行的性质:过直线外一点画已知直线的平行线,有且只有一条直线与已知直线平行;据此解答即可。
【详解】在同一平面内,过直线外一点画已知直线的平行线,可以画1条。
故答案为:A
【点睛】此题考查的知识点是平行的性质,关键是正确理解和运用。
10.C
【分析】只有一组对边平行的四边形叫做梯形。互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边是梯形的腰。从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高,据此解答。
【详解】A.梯形是一组对边平行,平行四边形是两组对边平行,所以原题表达错误;
B.互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边是梯形的腰,所以原题表达错误;
C.梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线用三角板的直角可以画出梯形的一条高,所以原题表达正确;
D.有一组对边平行的四边形叫梯形,所以原题表达错误。
故答案为:C
11. 不相交 互相平行 互相垂直 垂线 垂足
【分析】两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足;同一平面内不相交的两条直线互相平行,其中一条直线是另一条直线的平行线,据此解答。
【详解】根据分析可知,在同一个平面内不相交的两条直线叫作平行线,也可以说这两条直线互相平行。如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
12. 3 8
【分析】有两组对边平行的四边形叫作平行四边形;只有一组对边平行的四边形叫作梯形;据此数清楚图形即可。
【详解】数一数,图中有3个平行四边形,有8个梯形。
13. 8 易变形
【分析】从平行四边形的一条边上的任意一点都可以向对边作垂直线段,即是平行四边形的高;平行四边形具有易变形的特性,据此填空即可。
【详解】丽丽在图中的平行四边形的A点出发画了两条高,BC边上的高是8厘米。平行四边形具有易变形的特性,伸缩门就是利用这种特性制作。
14. 4 5 8
【分析】从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底,依此填空即可。
【详解】根据分析可知,平行四边形中,如果以10厘米的边为底,则高是4厘米;如果以5厘米的边为底,则高是8厘米。
【点睛】熟练掌握平行四边形的高的特点是解答此题的关键。
15. 无数 容易变形
【分析】根据梯形高的含义:梯形有一组对边平行,在这组对边里,可以画无数条垂直线段,所以有无数条高;由平行四边形的特性可知,平行四边形具有不稳定性,所以容易变形,伸缩门应用了平行四边形易变形的特性。
【详解】一个梯形中可以画无数条高,伸缩门应用了平行四边形的容易变形特性。
16.240
【分析】从直线外一点到这条直线上各点所连的线段中,垂直线段最短。则从一条小路到图书馆的3条小路中,与图书馆垂直的小路长度最短。比较三条路长度大小,找出最短的那条小路即可。
【详解】240<385<504,则这条小路的长度是240米。
17.AD
【分析】从直线外一点到这条直线所画的垂直线段的长度叫这点到这条直线的距离。这个点与垂足之间的线段叫做垂线段。过一点有且只有一条直线与已知直线垂直。从直线外一点到这条直线上各点所连的线段中,垂线段最短。
【详解】根据分析可知,从直线外点A引出的四条线段AB、AC、AD、AE中,最短的一条线段是AD。
18.相等
【分析】平行线的特征:两直线互相平行时,从一条直线上任意一点向另一条直线作垂线,所得的平行线间的垂直线段的长度,叫做平行线间的距离;平行线之间的距离处处相等;据此解答。
【详解】根据分析如图:
所以平行线间的距离处处相等。
19. 变形 不稳定
【分析】四边形易变形,具有不稳定性,人们在实际生活有很多应用,例如伸缩门、升降机、衣帽架等,据此即可解答。
【详解】用四根木条钉成一个四边形,轻轻一拉,这个四边形容易变形,说明四边形具有 不稳定性。
【点睛】本题主要考查学生对四边形的特征及性质的掌握和灵活运用。
20. 小林 直线外一点到直线上各点的连线中,垂线段最短
【分析】直线外一点到直线上各点的连线中,垂线段最短,据此填空即可。
【详解】小林家离学校最近,这是因为直线外一点到直线上各点的连线中,垂线段最短。
21.√
【分析】两条直线相交形成的角是90°,我们就说这两条直线互相垂直。根据垂直的定义,即可解答。
【详解】下午3时,钟面上的时针和分针形成的角是一个直角,因此时针和分针互相垂直。原题说法正确。
故答案为:√
【点睛】本题主要考查垂直的定义,属于基础知识,要熟练掌握。
22.√
【分析】平行四边形的对边平行且相等,依此画出一个平行四边形,再用量角器测量出四个角的度数,并根据测量结果进行判断即可。
【详解】画图如下:
由此可知,平行四边形的对角分别相等。
故答案为:√
23.√
【分析】同一平面内,永不相交的两条直线叫做平行线;两条平行线间的所有垂线段都相等;依此判断。
【详解】根据分析可知,a∥b,那么直线a与直线b之间的3条线段的长度都相等。
故答案为:√
24.√
【分析】同一平面内过已知直线上1个点仅有一条垂线,直线上有无数个点,所以同一平面内,任意一条直线的垂线有无数条。
【详解】根据分析同一平面内,任意一条直线的垂线有无数条,说法正确。
故答案为:√
【点睛】理解垂直关系是解答本题的关键。
25.×
【分析】根据画平行线的规律可知:过直线外一点画已知直线的平行线只能画一条。
【详解】过直线外一点画已知直线的平行线只能画一条。
所以原题说法错误。
故答案为:×
26.113°;67°;113°;67°;
∠1=∠3,∠2=∠4,且∠1与∠2、∠3与∠4的和都为180°,180°刚好为一个平角的度数;(答案不唯一)
【分析】先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此测量;再根据测量出的结果进行解答即可。
【详解】经过测量,填空如下:
∠1=113°,∠2=67°,∠3=113°,∠4=67°。
我发现:∠1=∠3,∠2=∠4;且∠1与∠2、∠3与∠4的和都为180°,180°刚好为一个平角的度数。(答案不唯一)
【点睛】熟练掌握角的度量方法以及平角的特点,是解答此题的关键。
27.15米、4米、15米
【分析】平行四边形的对边平行且相等,因此其余三条边有一条边是4米,则用38米减去2个4米后,再除以2即可得到与4米相邻的边的长度,依此计算并解答即可。
【详解】38-4-4=30(米)
30÷2=15(米)
答:其余三条边的长分别是15米、4米、15米。
【点睛】熟练掌握平行四边形的特点,是解答此题的关键。
28.见详解
【分析】根据线段、射线和直线的含义:线段有两个端点,不能向两端延伸,可以量出长度;射线只有一个端点,只能向一端无限延伸,不能量出长度;直线没有端点,可以向两端无限延伸,不能量出长度;同一平面内两条直线的位置关系:在同一平面内的两条不重合的直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况;据此解答。
【详解】直线有0个端点,可以向两边无限延长,不能测量长度﹔射线是直线的一部分,有1个端点,可以向一边无限延长,不能测量长度;线段是直线的一部分,有2个端点,可以测量长度;
同一平面内的两条直线不是相交就是平行,所以有两种位置关系:相交、平行。
29.见详解
【分析】从平行线上的任意一点到另一点的垂直线段叫做平行线间的距离。画垂直线段时,要用三角尺的直角去比着画。通过测量画出来的线段,发现这些线段的长度都相等。最后用这个发现来验证下面三个图形中的两条线是否互相平行。
【详解】
发现:平行线间的距离处处相等。
通过验证发现三个图形中的直线a、b互相平行。
【点睛】本题考查学生对于平行线距离的掌握。平行线间距离处处相等,我们可以用这个知识点来判断一组直线是否平行。
30.60个
【分析】此题考查的知识点是组合图形中平行四边形的计数,本题可根据平行四边形的定义,直接从图中数出平行四边形的个数,但数时应有一定的规律,以避免重复。根据平行四边形的定义可知,单个平行四边形有12个(假设有一个基本的方格构成的平行四边形)。2个平行四边形组成的平行四边形有24个。3个平行四边形组成的平行四边形有10个。4个平行四边形组成的平行四边形有6个。6个平行四边形组成的平行四边形有6个。8个平行四边形组成的平行四边形有2个。
【详解】根据分析得:12+24+10+6+6+2= 60(个)
答:图中共有60个平行四边形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五单元平行四边形和梯形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.把一张长方形纸连续对折两次后展开,三条折痕( )。
A.互相平行 B.互相垂直 C.相交 D.可能互相平行,也可能互相垂直
2.把一张长方形纸向同一个方向连续对折两次,形成的折痕的位置关系是( )。
A.互相平行 B.互相垂直 C.互相平行或互相垂直
3.下面( )组两直线相互垂直。
A. B. C. D.
4.过直线外一点画已知直线的垂线,可以画( )条。
A.1 B.2 C.无数
5.一个等腰梯形的上、下底之和是26厘米,周长是40厘米,则这个等腰梯形的一条腰长是( )厘米。
A.14 B.13 C.8 D.7
6.如图,三只小鸡同时发现了一条害虫,于是以同样的速度向害虫跑过去:( )最先吃到害虫。
A.小鸡1 B.小鸡2 C.小鸡3
7.捏住平行四边形的两个对角,向相反方向拉,它的周长( )。
A.不变 B.变短 C.变长 D.无法判断
8.下列图形中所作的高正确的是( )。
A. B. C. D.
9.从直线外一点画已知直线的平行线,可以画( )条。
A.1 B.2 C.3 D.无数条
10.下列说法中正确的是( )。
A.梯形是一种特殊的平行四边形
B.在梯形中,平行的一组对边叫作梯形的腰
C.直角梯形有无数条高
D.只有一组对边平行的图形都是梯形
二、填空题
11.在同一个平面内( )的两条直线叫作平行线,也可以说这两条直线( )。如果两条直线相交成直角,就说这两条直线( ),其中一条直线叫作另一条直线的( ),这两条直线的交点叫作( )。
12.数一数,如图中有( )个平行四边形,有( )个梯形。
13.丽丽在图中的平行四边形的A点出发画了两条高,BC边上的高是( )厘米。平行四边形具有( )的特性,伸缩门就是利用这种特性制作。
14.下图平行四边形中,如果以10厘米的边为底,则高是( )厘米;如果以( )厘米的边为底,则高是( )厘米。
15.一个梯形中可以画( )条高,伸缩门应用了平行四边形的( )特性。
16.周末,菲菲要到盘州市图书馆看书,她家到图书馆有三条路可以通往,长度分别是385米、504米、240米,其中一条小路与图书馆的位置垂直,则这条小路的长度是( )米。
17.图中从直线外点A引出的四条线段AB、AC、AD、AE中,最短的一条线段是( )。
18.平行线间的距离处处( )。
19.用四根木条钉成一个四边形,轻轻一拉,这个四边形容易( ),说明四边形具有( )性。
20.有四位同学的家在同一条街道上,如下图,( )家离学校最近,这是因为( )。
三、判断题
21.下午3时,钟面上的时针和分针互相垂直。( )
22.平行四边形的对角分别相等。( )
23.如图,a∥b,那么直线a与直线b之间的3条线段的长度都相等。( )
24.同一平面内,任意一条直线的垂线有无数条。( )
25.过直线外一点画已知直线的平行线,可以画无数条。( )
四、解答题
26.量出下图中四个角的度数,并说说你有什么发现。
∠1=( ),∠2=( ),∠3=( ),∠4=( )。
我发现:
27.公园里有一个花坛的形状是平行四边形,它的周长是38米,其中一条边长为4米,其余三条边的长分别是多少米?
28.直线、射线和线段有什么联系和区别?同一平面内的两条直线有哪几种位置关系?
29.下图中,a∥b。在a上任选几个点,分别向b画垂直的线段。量一量这些垂线段的长度,你发现了什么?
请用发现的规律,检验下面各组直线a、b是否平行。
30.数一数,图中共有多少个平行四边形?
《第五单元平行四边形和梯形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D A D B A D A C
1.A
【分析】把一张长方形的纸对折两次,两次折痕的位置关系,取决于对折的方向,一种情况是沿一条边的同一个方向对折两次,三条折痕是互相平行的;另一种情况是沿两条边的两个方向对折,两条折痕的互相垂直的;由此得出结论。
【详解】一张长方形纸沿一个方向连续对折两次后展开,三条折痕互相平行。
故答案为:A
【点睛】解答本题的关键在于要从不同的折叠方形考虑,具体操作一下会更简捷。
2.A
【分析】同一平面内两条直线的位置关系:在同一平面内的两条不重合的直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况;平行的概念:同一平面内不相交的两条直线互相平行,其中一条直线是另一条直线的平行线;垂直的概念:两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线;据此解答。
【详解】根据分析如图:
把一张长方形纸向同一个方向连续对折两次,形成的折痕的位置关系是互相平行。
故答案为:A
3.D
【分析】在同一个平面内,不相交的两条直线叫做平行线,两条直线相交成直角时,就说这两条直线互相垂直,那么其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足;由此求解。
【详解】
A.两直线不互相平行,也不互相垂直;
B.两直线相交,但不互相垂直;
C.两直线互相平行;
D.两直线相互垂直。
故答案为:D
【点睛】解决本题关键是熟练掌握平行和垂直的定义。
4.A
【分析】过直线上或直线外一点作作垂线的步骤:把三角尺的一条直角边与已知直线重合,沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上,沿三角尺的另一条直角边画一条直线,并画上垂直符号,这条直线就是已知直线的垂线。
【详解】通过分析可知:过直线外一点画已知直线的垂线可以画1条,过直线上一点画已知直线的垂线可以画1条。
故答案为:A
5.D
【分析】等腰梯形的两腰相等,这个梯形的周长减去上下底之和,再除以2即可算出它的一条腰长几厘米。
【详解】(40-26)÷2
=14÷2
=7(厘米)
则这个等腰梯形的一条腰长是7厘米。
故答案为:D
6.B
【分析】根据直线外一点到直线上各点的连线中,垂线段最短可知,小鸡2到害虫的距离最短,三只小鸡以同样的速度向害虫跑过去,小鸡2最先到达害虫位置,所以小鸡2最先吃到害虫,据此即可解答。
【详解】根据分析可知,三只小鸡同时发现了一条害虫,于是以同样的速度向害虫跑过去:小鸡2最先吃到害虫。
故答案为:B
7.A
【分析】平行四边形一旦确定,其四条边的长度也就确定了,由于平行四边形具有不稳定的特征,故其可以伸缩,但是无论怎么伸缩,其边的长度不变,据此解答即可。
【详解】捏住平行四边形的两个对角,向相反方向拉,虽然图形的形状变了,其边的长度不变,则其周长也不会发生改变。
故答案选:A
8.D
【分析】从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。
从三角形任一顶点向它的对边或者对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高。
从平行四边形的一条边上的任意一点都可以向对边作垂直线段,即是平行四边形的高。
【详解】A.不是从一条底边到它对边的垂直线段,不是梯形的高;
B.不是从顶点向它的对边的垂直线段,不是三角形的高;
C.不是垂直线段,不是平行四边形的高;
D.是从顶点到它的对边的垂直线段,是三角形的高。
故答案为:D
9.A
【分析】根据平行的性质:过直线外一点画已知直线的平行线,有且只有一条直线与已知直线平行;据此解答即可。
【详解】在同一平面内,过直线外一点画已知直线的平行线,可以画1条。
故答案为:A
【点睛】此题考查的知识点是平行的性质,关键是正确理解和运用。
10.C
【分析】只有一组对边平行的四边形叫做梯形。互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边是梯形的腰。从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高,据此解答。
【详解】A.梯形是一组对边平行,平行四边形是两组对边平行,所以原题表达错误;
B.互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边是梯形的腰,所以原题表达错误;
C.梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线用三角板的直角可以画出梯形的一条高,所以原题表达正确;
D.有一组对边平行的四边形叫梯形,所以原题表达错误。
故答案为:C
11. 不相交 互相平行 互相垂直 垂线 垂足
【分析】两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足;同一平面内不相交的两条直线互相平行,其中一条直线是另一条直线的平行线,据此解答。
【详解】根据分析可知,在同一个平面内不相交的两条直线叫作平行线,也可以说这两条直线互相平行。如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
12. 3 8
【分析】有两组对边平行的四边形叫作平行四边形;只有一组对边平行的四边形叫作梯形;据此数清楚图形即可。
【详解】数一数,图中有3个平行四边形,有8个梯形。
13. 8 易变形
【分析】从平行四边形的一条边上的任意一点都可以向对边作垂直线段,即是平行四边形的高;平行四边形具有易变形的特性,据此填空即可。
【详解】丽丽在图中的平行四边形的A点出发画了两条高,BC边上的高是8厘米。平行四边形具有易变形的特性,伸缩门就是利用这种特性制作。
14. 4 5 8
【分析】从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底,依此填空即可。
【详解】根据分析可知,平行四边形中,如果以10厘米的边为底,则高是4厘米;如果以5厘米的边为底,则高是8厘米。
【点睛】熟练掌握平行四边形的高的特点是解答此题的关键。
15. 无数 容易变形
【分析】根据梯形高的含义:梯形有一组对边平行,在这组对边里,可以画无数条垂直线段,所以有无数条高;由平行四边形的特性可知,平行四边形具有不稳定性,所以容易变形,伸缩门应用了平行四边形易变形的特性。
【详解】一个梯形中可以画无数条高,伸缩门应用了平行四边形的容易变形特性。
16.240
【分析】从直线外一点到这条直线上各点所连的线段中,垂直线段最短。则从一条小路到图书馆的3条小路中,与图书馆垂直的小路长度最短。比较三条路长度大小,找出最短的那条小路即可。
【详解】240<385<504,则这条小路的长度是240米。
17.AD
【分析】从直线外一点到这条直线所画的垂直线段的长度叫这点到这条直线的距离。这个点与垂足之间的线段叫做垂线段。过一点有且只有一条直线与已知直线垂直。从直线外一点到这条直线上各点所连的线段中,垂线段最短。
【详解】根据分析可知,从直线外点A引出的四条线段AB、AC、AD、AE中,最短的一条线段是AD。
18.相等
【分析】平行线的特征:两直线互相平行时,从一条直线上任意一点向另一条直线作垂线,所得的平行线间的垂直线段的长度,叫做平行线间的距离;平行线之间的距离处处相等;据此解答。
【详解】根据分析如图:
所以平行线间的距离处处相等。
19. 变形 不稳定
【分析】四边形易变形,具有不稳定性,人们在实际生活有很多应用,例如伸缩门、升降机、衣帽架等,据此即可解答。
【详解】用四根木条钉成一个四边形,轻轻一拉,这个四边形容易变形,说明四边形具有 不稳定性。
【点睛】本题主要考查学生对四边形的特征及性质的掌握和灵活运用。
20. 小林 直线外一点到直线上各点的连线中,垂线段最短
【分析】直线外一点到直线上各点的连线中,垂线段最短,据此填空即可。
【详解】小林家离学校最近,这是因为直线外一点到直线上各点的连线中,垂线段最短。
21.√
【分析】两条直线相交形成的角是90°,我们就说这两条直线互相垂直。根据垂直的定义,即可解答。
【详解】下午3时,钟面上的时针和分针形成的角是一个直角,因此时针和分针互相垂直。原题说法正确。
故答案为:√
【点睛】本题主要考查垂直的定义,属于基础知识,要熟练掌握。
22.√
【分析】平行四边形的对边平行且相等,依此画出一个平行四边形,再用量角器测量出四个角的度数,并根据测量结果进行判断即可。
【详解】画图如下:
由此可知,平行四边形的对角分别相等。
故答案为:√
23.√
【分析】同一平面内,永不相交的两条直线叫做平行线;两条平行线间的所有垂线段都相等;依此判断。
【详解】根据分析可知,a∥b,那么直线a与直线b之间的3条线段的长度都相等。
故答案为:√
24.√
【分析】同一平面内过已知直线上1个点仅有一条垂线,直线上有无数个点,所以同一平面内,任意一条直线的垂线有无数条。
【详解】根据分析同一平面内,任意一条直线的垂线有无数条,说法正确。
故答案为:√
【点睛】理解垂直关系是解答本题的关键。
25.×
【分析】根据画平行线的规律可知:过直线外一点画已知直线的平行线只能画一条。
【详解】过直线外一点画已知直线的平行线只能画一条。
所以原题说法错误。
故答案为:×
26.113°;67°;113°;67°;
∠1=∠3,∠2=∠4,且∠1与∠2、∠3与∠4的和都为180°,180°刚好为一个平角的度数;(答案不唯一)
【分析】先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此测量;再根据测量出的结果进行解答即可。
【详解】经过测量,填空如下:
∠1=113°,∠2=67°,∠3=113°,∠4=67°。
我发现:∠1=∠3,∠2=∠4;且∠1与∠2、∠3与∠4的和都为180°,180°刚好为一个平角的度数。(答案不唯一)
【点睛】熟练掌握角的度量方法以及平角的特点,是解答此题的关键。
27.15米、4米、15米
【分析】平行四边形的对边平行且相等,因此其余三条边有一条边是4米,则用38米减去2个4米后,再除以2即可得到与4米相邻的边的长度,依此计算并解答即可。
【详解】38-4-4=30(米)
30÷2=15(米)
答:其余三条边的长分别是15米、4米、15米。
【点睛】熟练掌握平行四边形的特点,是解答此题的关键。
28.见详解
【分析】根据线段、射线和直线的含义:线段有两个端点,不能向两端延伸,可以量出长度;射线只有一个端点,只能向一端无限延伸,不能量出长度;直线没有端点,可以向两端无限延伸,不能量出长度;同一平面内两条直线的位置关系:在同一平面内的两条不重合的直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况;据此解答。
【详解】直线有0个端点,可以向两边无限延长,不能测量长度﹔射线是直线的一部分,有1个端点,可以向一边无限延长,不能测量长度;线段是直线的一部分,有2个端点,可以测量长度;
同一平面内的两条直线不是相交就是平行,所以有两种位置关系:相交、平行。
29.见详解
【分析】从平行线上的任意一点到另一点的垂直线段叫做平行线间的距离。画垂直线段时,要用三角尺的直角去比着画。通过测量画出来的线段,发现这些线段的长度都相等。最后用这个发现来验证下面三个图形中的两条线是否互相平行。
【详解】
发现:平行线间的距离处处相等。
通过验证发现三个图形中的直线a、b互相平行。
【点睛】本题考查学生对于平行线距离的掌握。平行线间距离处处相等,我们可以用这个知识点来判断一组直线是否平行。
30.60个
【分析】此题考查的知识点是组合图形中平行四边形的计数,本题可根据平行四边形的定义,直接从图中数出平行四边形的个数,但数时应有一定的规律,以避免重复。根据平行四边形的定义可知,单个平行四边形有12个(假设有一个基本的方格构成的平行四边形)。2个平行四边形组成的平行四边形有24个。3个平行四边形组成的平行四边形有10个。4个平行四边形组成的平行四边形有6个。6个平行四边形组成的平行四边形有6个。8个平行四边形组成的平行四边形有2个。
【详解】根据分析得:12+24+10+6+6+2= 60(个)
答:图中共有60个平行四边形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
