3.4角的分类同步练习(含解析)人教版数学四年级上册
文档属性
| 名称 | 3.4角的分类同步练习(含解析)人教版数学四年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 427.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 20:41:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.4角的分类
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,将一张长方形纸折起一个三角形。如果∠2=120°,那么∠1=( )。
A.60° B.45° C.30°
2.把一个钝角分成两个角,其中一个是锐角,另一个( )。
A.一定是锐角 B.一定是直角
C.不可能是钝角 D.锐角、直角和钝角都有可能
3.150°是一个( )。
A.平角 B.锐角 C.钝角
4.下面说法正确的是( )。
A.射线是直线的一部分,所以射线比直线短。
B.把一个30度的角放在10倍放大镜下观察,角变成300°。
C.一个九位数,它的最高位的计数单位是亿位。
D.在6和7之间添上7个0,这个数才能成为六亿零七。
5.两个角正好组成一个平角,如果其中一个角是锐角,另一个角一定是( )。
A.锐角 B.直角 C.钝角
6.7点整时,钟面上时针与分针较小的夹角是( )。
A.锐角 B.直角 C.钝角 D.平角
7.把一个平角分成两个角,其中一个是钝角,那么另一个角一定是( )。
A.锐角 B.直角 C.钝角
8.上午9:30,钟面上时针和分针组成的角是( )。
A.锐角 B.钝角 C.直角 D.平角
9.下列说法错误的是( )。
A.一条线段长6厘米 B.从3:00到3:15,分针转动了90°
C.大于90°的角一定是钝角 D.两个钝角不可能拼成一个平角
10.已知∠1+∠2=∠3,∠1+∠2+∠3=180°,则∠3是( )。
A.锐角 B.直角 C.钝角
二、填空题
11.把下面各度数填在相应的括号。15°、166°、180°、91°、360°、90°、116°、4°。
锐角:( ),钝角:( ),直角:( ),平角:( ),周角:( )。
12.拨动钟面学具时针和分针,按要求填写时针和分针成什么角。
9时整,时针与分针形成的角是( )角;
2时整,时针与分针形成的角是( )角;
6时整,时针与分针形成的角是( )角;
5时整,时针与分针形成的角是( )角;
12时整,时针与分针形成的角是( )角。
13.如图,沿着一条直线摆了一副三角尺,∠2=45°,则∠1=( )°,∠3=( )°。
14.如图,已知其中一个角是120°,则∠1=( ),∠2=( )。
15.如图中,如果∠1=25°,那么∠2=( )°,∠3=( )°。
16.∠1+直角+25°=平角,则∠1=( )°,一个周角等于( )个直角。118°的角比平角少( )°。
17.说出每个钟面上时针和分针所构成的角的名称。
18.6整时,时针与分针所成的角度是( )度,是 ( )角。
19.钟面上8时55分时,时针与分针所形成的角是( )角,再过5分钟,时针与分针所形成的角是( )度。
20.跳水是一项优美的水上运动。在跳水比赛中,向后翻腾三周半抱膝,指的是运动员身体向后翻转( )°。
三、判断题
21.长方形或正方形的4个角都是直角,每个角的度数都是90°。( )
22.把一个平角分成两个角,如果一个是钝角,那么另一个一定是锐角。( )
23.平角+平角=周角。( )
24.一个钝角和一个锐角的和一定大于一个平角。( )
25.两个直角可以拼成一个钝角。( )
四、计算题
26.如下图,∠1=32°,请计算出∠2、∠3、∠4、∠5的度数。
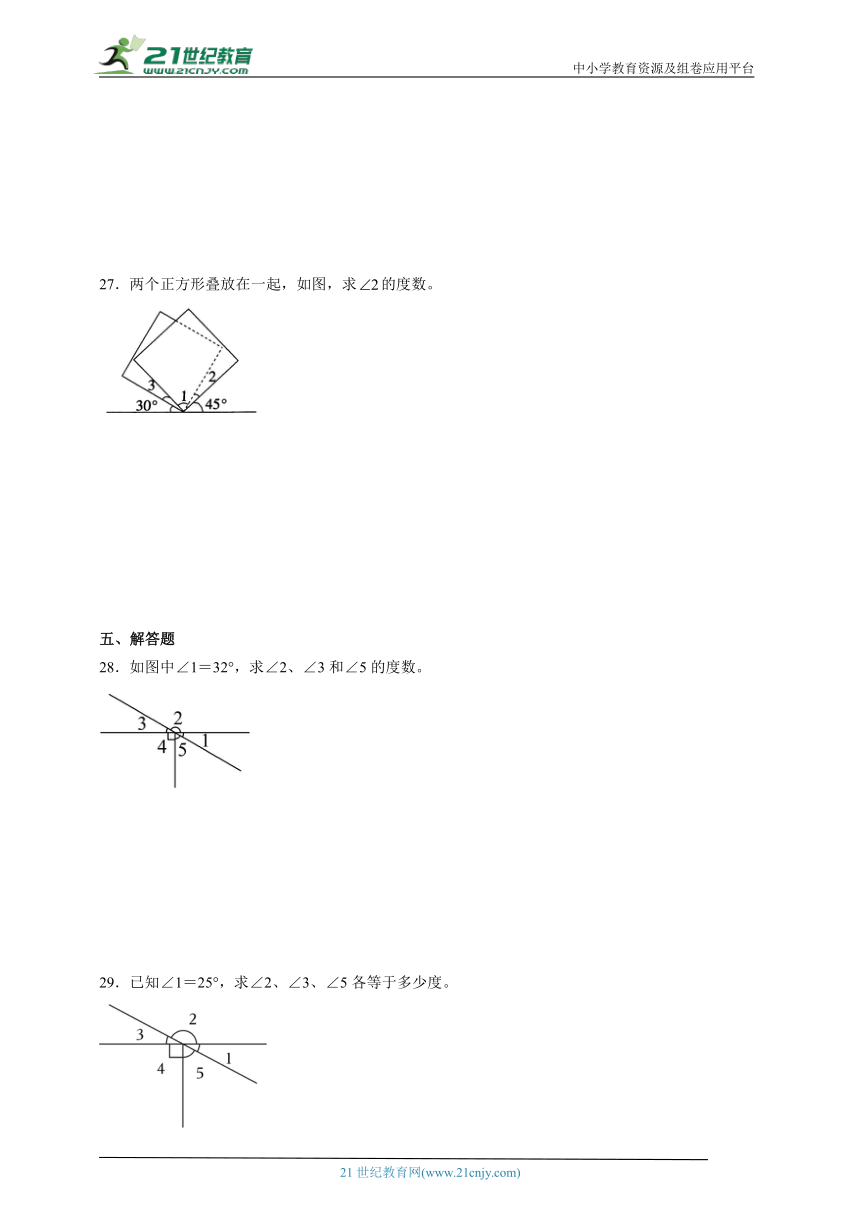
27.两个正方形叠放在一起,如图,求的度数。
五、解答题
28.如图中∠1=32°,求∠2、∠3和∠5的度数。
29.已知∠1=25°,求∠2、∠3、∠5各等于多少度。
30.体育课上,老师的口号“向后转”就是让同学旋转180°。你知道体育课上还有哪些有趣的角,并说说它们都属于什么角?
31.将一张圆形纸对折三次后展开,可以得到哪些度数的角?
32.已知∠3=60°,∠5=30°。求∠1、∠2、∠4的度数。
《3.4角的分类》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C D C C A B C B
1.C
【分析】根据图示三角形的长方形的一角折叠形成的,所以∠1与∠2中间的角与∠1相等,这个角又与∠1和∠2组成一个平角,根据平角=180°,且已知∠2的度数,即可算出∠1的度数,据此解答。
【详解】根据分析∠1×2+∠2=180°
则∠1=(180°-∠2)÷2
=(180°-120°)÷2
=60°÷2
=30°
所以∠1=30°
故答案为:C
【点睛】解答本题的关键是找出∠1、∠2的关系。
2.D
【分析】钝角是大于90°小于180°的角;锐角是大于0°小于90°的角;直角是90°的角;据此判断即可。
【详解】当这个钝角是150°时,
150°=60°+90°,此时一个是锐角,另一个是直角;
150°=50°+100°,此时一个是锐角,另一个是钝角;
150°=70°+80°,此时一个是锐角,另一个也是锐角;
所以把一个钝角分成两个角,其中一个是锐角,另一个是锐角、直角和钝角都有可能。
故答案为:D
3.C
【分析】平角是从一个端点分别引出两条射线,这两条射线组成的角是180°,锐角是小于90°的角,钝角的度数是大于90°小于180°。
【详解】90°<钝角<180°,所以150°是一个钝角。
故答案为:C
4.D
【分析】直线没有端点,可以向两端无限延伸,不能度量长度;射线有一个端点,可以向一端无限延伸,不能度量长度;
角的大小与两条边的长短无关,只与角两条边张开的大小有关;
从右边起,亿位在第九位,它的计数单位是“亿”;
读亿以上的数时,先读亿级,再读万级,最后读个级,亿级、万级的数要按照个级的数的读法来读,再在末尾加上“亿”、“万”,每级末尾不管有几个0,都不读,其余数位有一个0或连续几个0,都只读一个。据此解答。
【详解】A.由分析可知,直线和射线都不能度量长度,所以无法比较它们的长度关系,选项错误;
B.把角放在放大镜下观看,放大的角两边的长度,角两边张开大小不变,角的大小不变,选项错误;
C.由分析可知,九位数的最高位是亿位,计数单位是“亿”,选项错误;
D.6和7之间添上7个0,这个数变成600000007,读作六亿零七,选项正确。
故答案为:D
5.C
【分析】小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角,等于180°的角是平角,可假设这个锐角是89°,依此计算并选择。
【详解】180°-89°=91°,91°>90°,即另一个角一定是钝角。
故答案为:C
【点睛】熟练掌握平角、直角、钝角的特点是解答此题的关键。
6.C
【分析】钟面上有12大格,每一大格对应的夹角是30°,7点整时,时针指向7,分针指向12,7到12有5大格,钟面上时针与分针较小的夹角是30°×5=150°,是钝角,据此即可解答。
【详解】根据分析可知,7点整时,钟面上时针与分针较小的夹角是钝角。
故答案为:C
【点睛】熟练掌握时钟相关知识是解答本题的关键。
7.A
【分析】平角是180°的角,钝角是小于180°且大于90°的角,若将平角分成两个角,其中一个角是钝角,钝角必然大于90°,另一个角则小于90°,小于90°的角是锐角。据此解答。
【详解】由分析得:
一个平角分成两个角,其中一个是钝角,那么另一个角一定是锐角。
故答案为:A
8.B
【分析】指针分别指向9和6时是直角,9:30,分针指向6,时针转过了9,所以比直角大,是钝角,据此分析。
【详解】
如图,上午9:30,钟面上时针和分针组成的角是钝角。
故答案为:B
【点睛】关键是掌握角的分类标准,大于90度小于180度的角是钝角。
9.C
【分析】(1)根据线段的定义:线段有2个端点,有限长,可以度量,据此作答;
(2)钟面上有12大格,每一大格对应的夹角是30°,从3:00到3:15,分针从12走到3,走了3大格,转动了30°×3=90°,据此作答;
(3)小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角,等于180°的角是平角,等于360°的角是周角,所以大于90°的角不一定是钝角,据此作答;
(4)大于90°小于180°的角是钝角,等于180°的角是平角,两个钝角拼起来一定大于一个平角,据此作答。
【详解】根据上述分析可得:
A.线段长6厘米,原题说法正确;
B.从3:00到3:15,分针转动了90°,原题说法正确;
C.90°的角可能是钝角,可能是平角,也可能是周角,原题说法错误;
D.钝角不可能拼成一个平角,原题说法正确。
故答案为:C
10.B
【分析】已知∠1+∠2=∠3,那么第二个算式中∠1+∠2+∠3=∠3+∠3,据此即可计算出∠3的度数,再根据小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角进行选择,据此即可解答。
【详解】∠1+∠2=∠3
∠1+∠2+∠3=180°
∠3+∠3=180°
∠3的度数为:180°÷2=90°
90°的角是直角,则∠3是直角。
故答案为:B
11. 15°,4° 166°,91°,116° 90° 180° 360°
【分析】根据角的度数判断角的种类,锐角大于0°小于90°,直角等于90°,钝角大于90°小于180°,平角等于180°,周角等于360°;据此解答。
【详解】锐角:(15°,4°),钝角:(166°,91°,116°),直角:(90°),平角:(180°),周角:(360°)。
12. 直 锐 平 钝 周
【分析】钟面1大格是30°,先计算出角度,再根据锐角小于90°,钝角大于90°而小于180°,直角=90°,平角的两条边在同一条直线上,周角的两边重合,据此来确定这是一个什么角。
9时整,时针指向9,分针指向12,此时时针与分针相隔3大格,30°乘3即可求出这个角的度数;
2时整,时针与分针相隔2大格,30°乘2即可求出度数;
6时整,时针与分针在一条直线上,此时所成的角是平角;
5时整,时针与分针相隔5大格,30°乘5即可求出度数;
12时整,时针与分针正好重合,此时所成的角是周角。
【详解】30°×3=90°,9时整,时针与分针形成的角是直角;
30°×2=60°,2时整,时针与分针形成的角是锐角;
6时整,时针与分针形成的角是平角;
30°×5=150°,5时整,时针与分针形成的角是钝角;
12时整,时针与分针形成的角是周角。
【点睛】此题重点考查学生对锐角、直角、钝角、周角、平角的认识。
13. 45 135
【分析】观察图形可知,∠1与∠2组成了一个直角,所以∠1=90°-∠2;∠2与∠3组成了一个平角,据此利用∠2的度数即可求出∠3=180°-∠2。
【详解】∠1=90°-∠2=90°-45°=45°;
∠3=180°-∠2=180°-45°=135°。
14. 60° 120°
【分析】通过观察图可知:∠1和120°角组成平角,平角=180°,所以∠1=180°-120°;∠1和∠2组成平角,所以∠2=180°-∠1。
【详解】∠1=180°-120°=60°
∠2=180°-∠1=180°-60°=120°
【点睛】解答此题的关键是利用图形中特殊角的度数,即平角是180°,进行计算即可解答。
15. 65 115
【分析】直角是90°的角,平角是180°的角,1平角=2直角。观察图形,发现∠1与∠2构成了一个直角,∠3与∠2构成了一个平角,要想求∠2有多少度,只需要用90°减去∠1的度数即可;要想求∠3的度数,只需要用180°减去∠2的度数即可。据此解答。
【详解】90°-25°=65°
180°-65°=115°
如果∠1=25°,那么∠2=65°,∠3=115°
16. 65 4 62
【分析】1直角=90°,∠1加90°再加25°的和是180°,用180°减90°,再减25°,即可求出∠1的度数,而1周角=360°,360除以90即可求出1周角是几个直角;1平角=180°,180°减118°,即可求出118°的角比平角少多少度。
【详解】∠1=180°-90°-25°=90°-25°=65°
360°÷90°=4(个)
180°-118°=62°
∠1+直角+25°=平角,则∠1=65°,一个周角等于4个直角。118°的角比平角少62°。
17.平角;周角;钝角;直角
【分析】观察上图可知,第一个钟面时针和分针在一条直线上,所形成的角是180°,是平角;第二个钟面,分针旋转一周,并与时针完全重合,所形成的角等于360°,是周角;第三个钟面时针和分针所形成的角大于90°小于180°,是钝角;第四个钟面时针和分针互相垂直,所形成的角等于90°,是直角。
【详解】根据分析写出角的名称,如下:
【点睛】熟练掌握角的分类知识是解答本题的关键。
18. 180 平
【分析】
先画出图形,确定时针和分针的位置;6点整,时针指向6,分针指向12,每相邻两个数字之间的夹角为30°,再数出时针与分针之间有几个大格,进一步求其度数即可。
【详解】
一共有6个大格,则时针与分针所成的角度是30°×6=180°,是平角。
【点睛】
本题考查钟表时针与分针的夹角在钟表问题中,要知道钟表12个数字,每相邻两个数字之间的夹角为30度。
19. 锐 90
【分析】钟面1圈是360°,钟面被平均分为12大格,1大格是30°,8时55分,时针指向8与9之间,更靠近9,分针指向11,时针与分针之间的间隔不到3大格,所以此时时针与分针之间的夹角是小于90°,即此时形成的角是锐角。再过5分钟,时针指向9,分针指向12,此时时针与分针之间间隔3大格,夹角为3个30°,据此解答。
【详解】30°×3=90°
钟面上8时55分时,时针与分针所形成的角是锐角,再过5分钟,时针与分针所形成的角是90度。
20.1260
【分析】翻转一周指的是运动员身体翻转一个周角,翻腾三周半就是翻转了3个周角和一个周角的一半。周角=360°,据此计算。
【详解】360°×3+360°÷2
=1080°+180°
=1260°
跳水是一项优美的水上运动。在跳水比赛中,向后翻腾三周半抱膝,指的是运动员身体向后翻转1260°。
21.√
【分析】长方形和正方形的特征是:都有四条边,相对的两条边相等(正方形四条边都相等),有四个角,四个角都是直角;90°的角是直角;据此判断即可。
【详解】根据分析可知,长方形或正方形的4个角都是直角,每个角的度数都是90°;原题说法正确。
故答案为:√
22.√
【分析】平角是等于180°的角,钝角是大于90°、小于180°的角,锐角是大于0°、小于90°的角。根据角的大小和分类,即可解答。
【详解】如果一个平角分成两个角,其中一个角是钝角,由于钝角是大于90°、小于180°的角,而平角是180°的角,分了一个钝角,则剩下的角肯定小于90°,且大于0°,根据分析可知,大于0°且小于90°的角是锐角。所以题目说法正确。
故答案为:√
【点睛】本题主要考查角的大小和角的分类,解决此题的关键是牢记平角的大小和角的分类标准。
23.√
【分析】根据平角、周角的含义进行解答,平角:等于180度的角;周角:等于360度的角;据此解答即可。
【详解】平角=180°,周角=360°,平角+平角=周角,因此原题说法正确
故答案为:√
24.×
【分析】小于90°的角为锐角,大于90°的角为钝角,平角的度数为180°,题中有关键词“一定”出现,我们只要举出不符合的任意一种情况,即存在一个钝角和一个锐角的和小于一个平角就可以证明题目是错的。
【详解】存在10°的锐角和100°的钝角,它们的和为10°+100°=110°,110°<180°,所以存在一个钝角和一个锐角的和小于一个平角。所以判断错误。
故答案为:×
25.×
【分析】如图:直角是90°,两个直角拼成的角是180°,是平角。
【详解】由分析可知,两个直角可以拼成一个平角,原题说法错误。
故答案为:×
【点睛】解决本题的关键是要明确直角是90°,平角是180°。
26.∠2=58°;∠3=90°;∠4=32°;∠5=148°
【分析】根据题图可知,∠1、∠2和∠3组成一个平角,而∠3是一个直角,则∠2=180°-∠1-∠3。∠1和∠5组成一个平角,则∠5=180°-∠1。∠5和∠4组成一个平角,则∠4=∠1。
【详解】∠2=180°-∠1-∠3=180°-32°-90°=58°
∠3=90°
∠4=∠1=32°
∠5=180°-∠1=148°
27.15°
【分析】1直角=90°,1平角=180°,根据题意可知,∠1+∠3=90°,∠1+∠3+45°+∠2+30°=180°,由此可知,∠2=180°-30°-45°-(∠1+∠3),依此计算。
【详解】∠2=180°-30°-45°-90°
=150°-45°-90°
=105°-90°
=15°
∠2是15°。
28.∠2是148°,∠3是32°,∠5是58°
【分析】由图可知:∠1和∠2的和是一个平角是180°,用180°减去∠1就是∠2的度数;∠2、∠3构成一个平角,再用180°减去∠2就是∠3的度数;∠1、∠5构成一个直角,再用90°减去∠1就是∠5的度数。
【详解】∠2=180°-∠1
=180°-32°
=148°
∠3=180°-∠2
=180°-148°
=∠32°
∠5=90°-∠4
=90°-32°
=58°
答:∠2是148°,∠3是32°,∠5是58°。
【点睛】解决本题关键理解直角、平角的特点以及度数。
29.155°;25°;65°
【分析】∠1和∠2合起来是平角,即为180°,已知∠1=25°,利用减法即可求得∠2的度数;∠3和∠2合起来是平角,即为180°,利用求得的∠2的度数,即可求得∠3的度数;∠1和∠5合起来是个直角,即为90°,根据∠1=25°即可求得∠5的度数。
【详解】∠1=25°
∠1+∠2=180°
∠2=180°-25°=155°
∠3+∠2=180°
∠3=180°-155°=25°
∠1+∠5=90°
∠5=90°-25°=65°
答:∠2=155°,∠3=25°∠5=65°。
30.见详解
【详解】体育课上还有口号“向左转”和“向右转”,都是让同学旋转90°。180°的角是平角,90°的角是直角。
31.180°、90°、45°、135°、225°、270°、315°、360°;
【分析】每对折一次就用当前角的度数除以2即可;对折一次得到的角的度数用360°除以2;对折两次得到的角的度数用对折一次得到的角的度数除以2;对折三次得到的角的度数用对折两次得到的角的度数除以2;由此可知,可以得到的角的度数为最后一次对折所得到角的度数的倍数,最后全部展开可得到一个周角,依此计算并解答。
【详解】对折1次:360°÷2=180°;
对折2次:180°÷2=90°;
对折3次:90°÷2=45°;
45°×3=135°;
45°×5=225°;
45°×6=270°;
45°×7=315°;
45°×8=360°;
答:将一张圆形纸对折三次后展开,可以得到的角的度数有:180°、90°、45°、135°、225°、270°、315°、360°。
【点睛】此题考查的是图形的折叠问题,熟练掌握周角的特点,是解答此题的关键。
32.60°;120°;90°
【分析】用平角的度数减去∠3和∠5的度数,即可求出∠4的度数,再用平角的度数减去∠3的度数,即可求出∠2的度数,用平角的度数减去∠2的度数,即可求出∠1的度数,代入数据计算。
【详解】∠2=180°-60°=120°
∠1=180°-120°=60°
∠4=180°-60°-30°=90°
答:∠1的度数是60°,∠2的度数是120°,∠4的度数是90°。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.4角的分类
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,将一张长方形纸折起一个三角形。如果∠2=120°,那么∠1=( )。
A.60° B.45° C.30°
2.把一个钝角分成两个角,其中一个是锐角,另一个( )。
A.一定是锐角 B.一定是直角
C.不可能是钝角 D.锐角、直角和钝角都有可能
3.150°是一个( )。
A.平角 B.锐角 C.钝角
4.下面说法正确的是( )。
A.射线是直线的一部分,所以射线比直线短。
B.把一个30度的角放在10倍放大镜下观察,角变成300°。
C.一个九位数,它的最高位的计数单位是亿位。
D.在6和7之间添上7个0,这个数才能成为六亿零七。
5.两个角正好组成一个平角,如果其中一个角是锐角,另一个角一定是( )。
A.锐角 B.直角 C.钝角
6.7点整时,钟面上时针与分针较小的夹角是( )。
A.锐角 B.直角 C.钝角 D.平角
7.把一个平角分成两个角,其中一个是钝角,那么另一个角一定是( )。
A.锐角 B.直角 C.钝角
8.上午9:30,钟面上时针和分针组成的角是( )。
A.锐角 B.钝角 C.直角 D.平角
9.下列说法错误的是( )。
A.一条线段长6厘米 B.从3:00到3:15,分针转动了90°
C.大于90°的角一定是钝角 D.两个钝角不可能拼成一个平角
10.已知∠1+∠2=∠3,∠1+∠2+∠3=180°,则∠3是( )。
A.锐角 B.直角 C.钝角
二、填空题
11.把下面各度数填在相应的括号。15°、166°、180°、91°、360°、90°、116°、4°。
锐角:( ),钝角:( ),直角:( ),平角:( ),周角:( )。
12.拨动钟面学具时针和分针,按要求填写时针和分针成什么角。
9时整,时针与分针形成的角是( )角;
2时整,时针与分针形成的角是( )角;
6时整,时针与分针形成的角是( )角;
5时整,时针与分针形成的角是( )角;
12时整,时针与分针形成的角是( )角。
13.如图,沿着一条直线摆了一副三角尺,∠2=45°,则∠1=( )°,∠3=( )°。
14.如图,已知其中一个角是120°,则∠1=( ),∠2=( )。
15.如图中,如果∠1=25°,那么∠2=( )°,∠3=( )°。
16.∠1+直角+25°=平角,则∠1=( )°,一个周角等于( )个直角。118°的角比平角少( )°。
17.说出每个钟面上时针和分针所构成的角的名称。
18.6整时,时针与分针所成的角度是( )度,是 ( )角。
19.钟面上8时55分时,时针与分针所形成的角是( )角,再过5分钟,时针与分针所形成的角是( )度。
20.跳水是一项优美的水上运动。在跳水比赛中,向后翻腾三周半抱膝,指的是运动员身体向后翻转( )°。
三、判断题
21.长方形或正方形的4个角都是直角,每个角的度数都是90°。( )
22.把一个平角分成两个角,如果一个是钝角,那么另一个一定是锐角。( )
23.平角+平角=周角。( )
24.一个钝角和一个锐角的和一定大于一个平角。( )
25.两个直角可以拼成一个钝角。( )
四、计算题
26.如下图,∠1=32°,请计算出∠2、∠3、∠4、∠5的度数。
27.两个正方形叠放在一起,如图,求的度数。
五、解答题
28.如图中∠1=32°,求∠2、∠3和∠5的度数。
29.已知∠1=25°,求∠2、∠3、∠5各等于多少度。
30.体育课上,老师的口号“向后转”就是让同学旋转180°。你知道体育课上还有哪些有趣的角,并说说它们都属于什么角?
31.将一张圆形纸对折三次后展开,可以得到哪些度数的角?
32.已知∠3=60°,∠5=30°。求∠1、∠2、∠4的度数。
《3.4角的分类》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C D C C A B C B
1.C
【分析】根据图示三角形的长方形的一角折叠形成的,所以∠1与∠2中间的角与∠1相等,这个角又与∠1和∠2组成一个平角,根据平角=180°,且已知∠2的度数,即可算出∠1的度数,据此解答。
【详解】根据分析∠1×2+∠2=180°
则∠1=(180°-∠2)÷2
=(180°-120°)÷2
=60°÷2
=30°
所以∠1=30°
故答案为:C
【点睛】解答本题的关键是找出∠1、∠2的关系。
2.D
【分析】钝角是大于90°小于180°的角;锐角是大于0°小于90°的角;直角是90°的角;据此判断即可。
【详解】当这个钝角是150°时,
150°=60°+90°,此时一个是锐角,另一个是直角;
150°=50°+100°,此时一个是锐角,另一个是钝角;
150°=70°+80°,此时一个是锐角,另一个也是锐角;
所以把一个钝角分成两个角,其中一个是锐角,另一个是锐角、直角和钝角都有可能。
故答案为:D
3.C
【分析】平角是从一个端点分别引出两条射线,这两条射线组成的角是180°,锐角是小于90°的角,钝角的度数是大于90°小于180°。
【详解】90°<钝角<180°,所以150°是一个钝角。
故答案为:C
4.D
【分析】直线没有端点,可以向两端无限延伸,不能度量长度;射线有一个端点,可以向一端无限延伸,不能度量长度;
角的大小与两条边的长短无关,只与角两条边张开的大小有关;
从右边起,亿位在第九位,它的计数单位是“亿”;
读亿以上的数时,先读亿级,再读万级,最后读个级,亿级、万级的数要按照个级的数的读法来读,再在末尾加上“亿”、“万”,每级末尾不管有几个0,都不读,其余数位有一个0或连续几个0,都只读一个。据此解答。
【详解】A.由分析可知,直线和射线都不能度量长度,所以无法比较它们的长度关系,选项错误;
B.把角放在放大镜下观看,放大的角两边的长度,角两边张开大小不变,角的大小不变,选项错误;
C.由分析可知,九位数的最高位是亿位,计数单位是“亿”,选项错误;
D.6和7之间添上7个0,这个数变成600000007,读作六亿零七,选项正确。
故答案为:D
5.C
【分析】小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角,等于180°的角是平角,可假设这个锐角是89°,依此计算并选择。
【详解】180°-89°=91°,91°>90°,即另一个角一定是钝角。
故答案为:C
【点睛】熟练掌握平角、直角、钝角的特点是解答此题的关键。
6.C
【分析】钟面上有12大格,每一大格对应的夹角是30°,7点整时,时针指向7,分针指向12,7到12有5大格,钟面上时针与分针较小的夹角是30°×5=150°,是钝角,据此即可解答。
【详解】根据分析可知,7点整时,钟面上时针与分针较小的夹角是钝角。
故答案为:C
【点睛】熟练掌握时钟相关知识是解答本题的关键。
7.A
【分析】平角是180°的角,钝角是小于180°且大于90°的角,若将平角分成两个角,其中一个角是钝角,钝角必然大于90°,另一个角则小于90°,小于90°的角是锐角。据此解答。
【详解】由分析得:
一个平角分成两个角,其中一个是钝角,那么另一个角一定是锐角。
故答案为:A
8.B
【分析】指针分别指向9和6时是直角,9:30,分针指向6,时针转过了9,所以比直角大,是钝角,据此分析。
【详解】
如图,上午9:30,钟面上时针和分针组成的角是钝角。
故答案为:B
【点睛】关键是掌握角的分类标准,大于90度小于180度的角是钝角。
9.C
【分析】(1)根据线段的定义:线段有2个端点,有限长,可以度量,据此作答;
(2)钟面上有12大格,每一大格对应的夹角是30°,从3:00到3:15,分针从12走到3,走了3大格,转动了30°×3=90°,据此作答;
(3)小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角,等于180°的角是平角,等于360°的角是周角,所以大于90°的角不一定是钝角,据此作答;
(4)大于90°小于180°的角是钝角,等于180°的角是平角,两个钝角拼起来一定大于一个平角,据此作答。
【详解】根据上述分析可得:
A.线段长6厘米,原题说法正确;
B.从3:00到3:15,分针转动了90°,原题说法正确;
C.90°的角可能是钝角,可能是平角,也可能是周角,原题说法错误;
D.钝角不可能拼成一个平角,原题说法正确。
故答案为:C
10.B
【分析】已知∠1+∠2=∠3,那么第二个算式中∠1+∠2+∠3=∠3+∠3,据此即可计算出∠3的度数,再根据小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角进行选择,据此即可解答。
【详解】∠1+∠2=∠3
∠1+∠2+∠3=180°
∠3+∠3=180°
∠3的度数为:180°÷2=90°
90°的角是直角,则∠3是直角。
故答案为:B
11. 15°,4° 166°,91°,116° 90° 180° 360°
【分析】根据角的度数判断角的种类,锐角大于0°小于90°,直角等于90°,钝角大于90°小于180°,平角等于180°,周角等于360°;据此解答。
【详解】锐角:(15°,4°),钝角:(166°,91°,116°),直角:(90°),平角:(180°),周角:(360°)。
12. 直 锐 平 钝 周
【分析】钟面1大格是30°,先计算出角度,再根据锐角小于90°,钝角大于90°而小于180°,直角=90°,平角的两条边在同一条直线上,周角的两边重合,据此来确定这是一个什么角。
9时整,时针指向9,分针指向12,此时时针与分针相隔3大格,30°乘3即可求出这个角的度数;
2时整,时针与分针相隔2大格,30°乘2即可求出度数;
6时整,时针与分针在一条直线上,此时所成的角是平角;
5时整,时针与分针相隔5大格,30°乘5即可求出度数;
12时整,时针与分针正好重合,此时所成的角是周角。
【详解】30°×3=90°,9时整,时针与分针形成的角是直角;
30°×2=60°,2时整,时针与分针形成的角是锐角;
6时整,时针与分针形成的角是平角;
30°×5=150°,5时整,时针与分针形成的角是钝角;
12时整,时针与分针形成的角是周角。
【点睛】此题重点考查学生对锐角、直角、钝角、周角、平角的认识。
13. 45 135
【分析】观察图形可知,∠1与∠2组成了一个直角,所以∠1=90°-∠2;∠2与∠3组成了一个平角,据此利用∠2的度数即可求出∠3=180°-∠2。
【详解】∠1=90°-∠2=90°-45°=45°;
∠3=180°-∠2=180°-45°=135°。
14. 60° 120°
【分析】通过观察图可知:∠1和120°角组成平角,平角=180°,所以∠1=180°-120°;∠1和∠2组成平角,所以∠2=180°-∠1。
【详解】∠1=180°-120°=60°
∠2=180°-∠1=180°-60°=120°
【点睛】解答此题的关键是利用图形中特殊角的度数,即平角是180°,进行计算即可解答。
15. 65 115
【分析】直角是90°的角,平角是180°的角,1平角=2直角。观察图形,发现∠1与∠2构成了一个直角,∠3与∠2构成了一个平角,要想求∠2有多少度,只需要用90°减去∠1的度数即可;要想求∠3的度数,只需要用180°减去∠2的度数即可。据此解答。
【详解】90°-25°=65°
180°-65°=115°
如果∠1=25°,那么∠2=65°,∠3=115°
16. 65 4 62
【分析】1直角=90°,∠1加90°再加25°的和是180°,用180°减90°,再减25°,即可求出∠1的度数,而1周角=360°,360除以90即可求出1周角是几个直角;1平角=180°,180°减118°,即可求出118°的角比平角少多少度。
【详解】∠1=180°-90°-25°=90°-25°=65°
360°÷90°=4(个)
180°-118°=62°
∠1+直角+25°=平角,则∠1=65°,一个周角等于4个直角。118°的角比平角少62°。
17.平角;周角;钝角;直角
【分析】观察上图可知,第一个钟面时针和分针在一条直线上,所形成的角是180°,是平角;第二个钟面,分针旋转一周,并与时针完全重合,所形成的角等于360°,是周角;第三个钟面时针和分针所形成的角大于90°小于180°,是钝角;第四个钟面时针和分针互相垂直,所形成的角等于90°,是直角。
【详解】根据分析写出角的名称,如下:
【点睛】熟练掌握角的分类知识是解答本题的关键。
18. 180 平
【分析】
先画出图形,确定时针和分针的位置;6点整,时针指向6,分针指向12,每相邻两个数字之间的夹角为30°,再数出时针与分针之间有几个大格,进一步求其度数即可。
【详解】
一共有6个大格,则时针与分针所成的角度是30°×6=180°,是平角。
【点睛】
本题考查钟表时针与分针的夹角在钟表问题中,要知道钟表12个数字,每相邻两个数字之间的夹角为30度。
19. 锐 90
【分析】钟面1圈是360°,钟面被平均分为12大格,1大格是30°,8时55分,时针指向8与9之间,更靠近9,分针指向11,时针与分针之间的间隔不到3大格,所以此时时针与分针之间的夹角是小于90°,即此时形成的角是锐角。再过5分钟,时针指向9,分针指向12,此时时针与分针之间间隔3大格,夹角为3个30°,据此解答。
【详解】30°×3=90°
钟面上8时55分时,时针与分针所形成的角是锐角,再过5分钟,时针与分针所形成的角是90度。
20.1260
【分析】翻转一周指的是运动员身体翻转一个周角,翻腾三周半就是翻转了3个周角和一个周角的一半。周角=360°,据此计算。
【详解】360°×3+360°÷2
=1080°+180°
=1260°
跳水是一项优美的水上运动。在跳水比赛中,向后翻腾三周半抱膝,指的是运动员身体向后翻转1260°。
21.√
【分析】长方形和正方形的特征是:都有四条边,相对的两条边相等(正方形四条边都相等),有四个角,四个角都是直角;90°的角是直角;据此判断即可。
【详解】根据分析可知,长方形或正方形的4个角都是直角,每个角的度数都是90°;原题说法正确。
故答案为:√
22.√
【分析】平角是等于180°的角,钝角是大于90°、小于180°的角,锐角是大于0°、小于90°的角。根据角的大小和分类,即可解答。
【详解】如果一个平角分成两个角,其中一个角是钝角,由于钝角是大于90°、小于180°的角,而平角是180°的角,分了一个钝角,则剩下的角肯定小于90°,且大于0°,根据分析可知,大于0°且小于90°的角是锐角。所以题目说法正确。
故答案为:√
【点睛】本题主要考查角的大小和角的分类,解决此题的关键是牢记平角的大小和角的分类标准。
23.√
【分析】根据平角、周角的含义进行解答,平角:等于180度的角;周角:等于360度的角;据此解答即可。
【详解】平角=180°,周角=360°,平角+平角=周角,因此原题说法正确
故答案为:√
24.×
【分析】小于90°的角为锐角,大于90°的角为钝角,平角的度数为180°,题中有关键词“一定”出现,我们只要举出不符合的任意一种情况,即存在一个钝角和一个锐角的和小于一个平角就可以证明题目是错的。
【详解】存在10°的锐角和100°的钝角,它们的和为10°+100°=110°,110°<180°,所以存在一个钝角和一个锐角的和小于一个平角。所以判断错误。
故答案为:×
25.×
【分析】如图:直角是90°,两个直角拼成的角是180°,是平角。
【详解】由分析可知,两个直角可以拼成一个平角,原题说法错误。
故答案为:×
【点睛】解决本题的关键是要明确直角是90°,平角是180°。
26.∠2=58°;∠3=90°;∠4=32°;∠5=148°
【分析】根据题图可知,∠1、∠2和∠3组成一个平角,而∠3是一个直角,则∠2=180°-∠1-∠3。∠1和∠5组成一个平角,则∠5=180°-∠1。∠5和∠4组成一个平角,则∠4=∠1。
【详解】∠2=180°-∠1-∠3=180°-32°-90°=58°
∠3=90°
∠4=∠1=32°
∠5=180°-∠1=148°
27.15°
【分析】1直角=90°,1平角=180°,根据题意可知,∠1+∠3=90°,∠1+∠3+45°+∠2+30°=180°,由此可知,∠2=180°-30°-45°-(∠1+∠3),依此计算。
【详解】∠2=180°-30°-45°-90°
=150°-45°-90°
=105°-90°
=15°
∠2是15°。
28.∠2是148°,∠3是32°,∠5是58°
【分析】由图可知:∠1和∠2的和是一个平角是180°,用180°减去∠1就是∠2的度数;∠2、∠3构成一个平角,再用180°减去∠2就是∠3的度数;∠1、∠5构成一个直角,再用90°减去∠1就是∠5的度数。
【详解】∠2=180°-∠1
=180°-32°
=148°
∠3=180°-∠2
=180°-148°
=∠32°
∠5=90°-∠4
=90°-32°
=58°
答:∠2是148°,∠3是32°,∠5是58°。
【点睛】解决本题关键理解直角、平角的特点以及度数。
29.155°;25°;65°
【分析】∠1和∠2合起来是平角,即为180°,已知∠1=25°,利用减法即可求得∠2的度数;∠3和∠2合起来是平角,即为180°,利用求得的∠2的度数,即可求得∠3的度数;∠1和∠5合起来是个直角,即为90°,根据∠1=25°即可求得∠5的度数。
【详解】∠1=25°
∠1+∠2=180°
∠2=180°-25°=155°
∠3+∠2=180°
∠3=180°-155°=25°
∠1+∠5=90°
∠5=90°-25°=65°
答:∠2=155°,∠3=25°∠5=65°。
30.见详解
【详解】体育课上还有口号“向左转”和“向右转”,都是让同学旋转90°。180°的角是平角,90°的角是直角。
31.180°、90°、45°、135°、225°、270°、315°、360°;
【分析】每对折一次就用当前角的度数除以2即可;对折一次得到的角的度数用360°除以2;对折两次得到的角的度数用对折一次得到的角的度数除以2;对折三次得到的角的度数用对折两次得到的角的度数除以2;由此可知,可以得到的角的度数为最后一次对折所得到角的度数的倍数,最后全部展开可得到一个周角,依此计算并解答。
【详解】对折1次:360°÷2=180°;
对折2次:180°÷2=90°;
对折3次:90°÷2=45°;
45°×3=135°;
45°×5=225°;
45°×6=270°;
45°×7=315°;
45°×8=360°;
答:将一张圆形纸对折三次后展开,可以得到的角的度数有:180°、90°、45°、135°、225°、270°、315°、360°。
【点睛】此题考查的是图形的折叠问题,熟练掌握周角的特点,是解答此题的关键。
32.60°;120°;90°
【分析】用平角的度数减去∠3和∠5的度数,即可求出∠4的度数,再用平角的度数减去∠3的度数,即可求出∠2的度数,用平角的度数减去∠2的度数,即可求出∠1的度数,代入数据计算。
【详解】∠2=180°-60°=120°
∠1=180°-120°=60°
∠4=180°-60°-30°=90°
答:∠1的度数是60°,∠2的度数是120°,∠4的度数是90°。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
