2.2 数轴 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 2.2 数轴 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 922.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 18:58:45 | ||
图片预览


文档简介
2.2 数 轴
第1课时 数轴的概念
1. 能正确地画出数轴,掌握数轴的三要素.
2. 能将已知数在数轴上表示出来,能指出数轴上的点所表示的数.
建议用时:15分钟
1 (2025盐城亭湖期末)下列选项中,表示数轴正确的是( )
A B C D
2 (2024无锡宜兴月考)如图,在数轴上,手掌遮挡住的点表示的数可能是( )
A. 0.5 B. -0.5 C. -1.5 D. -2.5
3 在数轴上,原点及原点左边的点所表示的数是( )
A. 正数 B. 负数 C. 非负数 D. 非正数
4 数轴上表示-4的点到原点的距离是 .
5 如图,数轴上最接近-π的是点 .
6 (2024淮安月考)如图,直径为1个单位长度的圆,圆上的一点A由原点沿数轴向右滚动一周(不滑动)到达点A′,则点A′表示的数是 .
(第6题) (第7题)
7 如图,面积为8的长方形ABCD的顶点A,B在数轴上,BC=1.6,点A对应的数为-1,则点B所对应的数为 W.
8 (1) 分别指出如图所示的数轴上A,B,C,D,E各点表示的有理数;
(2) 画出数轴并将下列各数标在数轴上:-2.5,,3,0.
建议用时:20+5分钟
9 (2025南通模拟)在数轴上,把表示-2的点沿着数轴移动7个单位长度得到的点所表示的数是( )
A. 5 B. -9 C. ±5 D. 5或-9
10 已知数轴上的点A到原点的距离为3,则数轴上到点A的距离是5的点所表示的数有( )
A. 1个 B. 2个 C. 3个 D. 4个
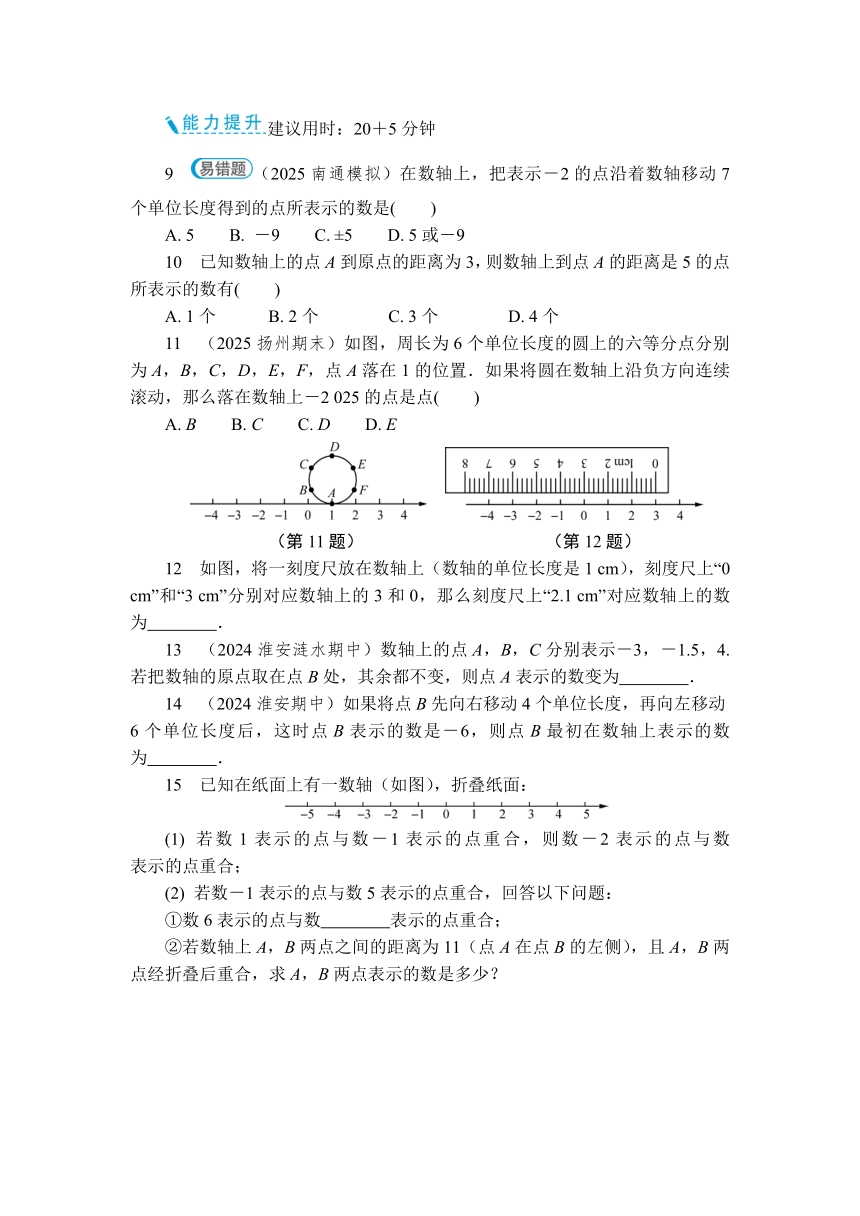
11 (2025扬州期末)如图,周长为6个单位长度的圆上的六等分点分别为A,B,C,D,E,F,点A落在1的位置.如果将圆在数轴上沿负方向连续滚动,那么落在数轴上-2 025的点是点( )
A. B B. C C. D D. E
(第11题) (第12题)
12 如图,将一刻度尺放在数轴上(数轴的单位长度是1 cm),刻度尺上“0 cm”和“3 cm”分别对应数轴上的3和0,那么刻度尺上“2.1 cm”对应数轴上的数为 .
13 (2024淮安涟水期中)数轴上的点A,B,C分别表示-3,-1.5,4.若把数轴的原点取在点B处,其余都不变,则点A表示的数变为 .
14 (2024淮安期中)如果将点B先向右移动4个单位长度,再向左移动6个单位长度后,这时点B表示的数是-6,则点B最初在数轴上表示的数为 .
15 已知在纸面上有一数轴(如图),折叠纸面:
(1) 若数1表示的点与数-1表示的点重合,则数-2表示的点与数 表示的点重合;
(2) 若数-1表示的点与数5表示的点重合,回答以下问题:
①数6表示的点与数 表示的点重合;
②若数轴上A,B两点之间的距离为11(点A在点B的左侧),且A,B两点经折叠后重合,求A,B两点表示的数是多少?
第2课时 有理数的大小
1. 会利用数轴比较有理数的大小,能正确地使用“>”或“<”连接.
2. 能初步进行有理数大小比较的推理和书写.
3. 能借助数轴解决数学中的问题,感受数形结合的思想,发展抽象能力和几何直观.
建议用时:15分钟
1 (2024甘肃)下列各数中,比-2小的数是( )
A. -1 B. -4 C. 4 D. 1
2 (2024广州)在四个数-10,-1,0,10中,最小的数是( )
A. -10 B. -1 C. 0 D. 10
3 (2024广安)下列各数中,最大的是( )
A. -2 B. - C. 0 D. 1
4 有理数m,n在数轴上的位置如图,则下列结论中正确的是( )
A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0
5 (2024辽宁)亚洲、欧洲、非洲和南美洲的最低海拔如表:
大洲 亚洲 欧洲 非洲 南美洲
最低海拔/m -415 -28 -156 -40
其中最低海拔最小的大洲是( )
A. 亚洲 B. 欧洲 C. 非洲 D. 南美洲
6 据中央气象台某天的预报,下列四个城市的最低气温分别是哈尔滨-11 ℃,杭州6 ℃,兰州 -5 ℃,海口27 ℃.其中,最低气温最高的城市为 ,最低气温最低的城市为 .
7 比较大小:- -.(填“>”“<”或“=”)
8 (2024南通海安月考)数轴上点A,B,C的位置如图所示.请回答下列问题:
(1) 表示有理数-3的点是点 ,将点C向左移动4个单位长度得到点C′,则点C′表示的有理数是 ;
(2) 在数轴上标出点D,E,其中点D,E分别表示有理数-和1.5;
(3) 将-3,0,-,1.5这四个数用“<”号连接的结果是 .
建议用时:20+5分钟
9 (2024连云港海州开学考试)小于-22且大于-24的整数为( )
A. -19 B. -23 C. -31 D. -22.1
10 下列比较两个数的大小中,正确的是( )
A. 1<-2 B. -<- C. 0<-0.1 D. -<-
11 从数轴上看,0是( )
A. 最小的整数 B. 最大的负数 C. 最小的有理数 D. 最小的非负数
12 (2024南京建邺月考)若在-0.154 8中用数字3替换其中的一个非零数字后,使所得的数最大,则被替换的数字是( )
A. 1 B. 5 C. 4 D. 8
13 (2024泰兴期中)关于有理数a,b,2,下列说法中正确的是( )
A. 如果a>2,a>b,那么b<2 B. 如果b<2,a>b,那么a>2
C. 如果a>2,b<2,那么a14 在-π,-1,-2,0中,比-3小的数是 .
15 比较大小:(1) - -;(2) - -π.(填“<”“>”或“=”)
16 (1) 最小的正整数是 ;(2) 最大的负整数是 .
17 (2025南通崇川期末)定义:[x]表示不大于x的最大整数.例如[1.6]=1,[π]= ,[-2.82]= .
18 写出符合条件的数,并将它们在数轴上表示出来:
(1) 大于-5且不大于-1的负整数;
(2) 大于-1的非正整数.
19 已知在数轴上有A,B,C三个点,点A表示的数是-4,点B表示的数是-2,点C表示的数是2.
(1) 在数轴上将A,B,C三点表示出来,并比较各数的大小(用“<”号连接);
(2) 如何移动点B,使它到点A和点C的距离相等.
2.2 数 轴
第1课时 数轴的概念
1. D 2. B 3. D 4. 4 5. B 6. π 7. 4
8. (1) 点A表示-4,点B表示-1,点C表示,
点D表示3,点E表示4.
(2) 如图所示:
9. D 10. D 11. D 12. 0.9 13. -1.5 14. -4
15. (1) 2
(2) ①-2
②因为A,B两点之间的距离为11,经折叠后重合,
所以点A,B距离对称中心的距离为11÷2=5.5.
由题意,得两点关于数2表示的点对称,点A在点B的左侧,
所以点B表示的数为2+5.5=7.5,点A表示的数为2-5.5=-3.5.
第2课时 有理数的大小
1. B 2. A 3. D 4. B 5. A 6. 海口 哈尔滨 7. <
8. (1) A -2
(2) 如图:
所以点D,E即为所求.
(3) -3<-<0<1.5
9. B 10. D 11. D 12. B 13. D 14. -π
15. (1) > (2) < 16. (1) 1 (2) -1 17. 3 -3
18. (1) -4,-3,-2,-1.
在数轴上的位置如图所示:
(2) -1,0.
在数轴上的位置如图所示:
19. (1) 在数轴上的位置如图所示:
根据数轴可知-4<-2<2.
(2) 点B向右移动一个单位长度,可得到它到点A和点C的距离相等.
第1课时 数轴的概念
1. 能正确地画出数轴,掌握数轴的三要素.
2. 能将已知数在数轴上表示出来,能指出数轴上的点所表示的数.
建议用时:15分钟
1 (2025盐城亭湖期末)下列选项中,表示数轴正确的是( )
A B C D
2 (2024无锡宜兴月考)如图,在数轴上,手掌遮挡住的点表示的数可能是( )
A. 0.5 B. -0.5 C. -1.5 D. -2.5
3 在数轴上,原点及原点左边的点所表示的数是( )
A. 正数 B. 负数 C. 非负数 D. 非正数
4 数轴上表示-4的点到原点的距离是 .
5 如图,数轴上最接近-π的是点 .
6 (2024淮安月考)如图,直径为1个单位长度的圆,圆上的一点A由原点沿数轴向右滚动一周(不滑动)到达点A′,则点A′表示的数是 .
(第6题) (第7题)
7 如图,面积为8的长方形ABCD的顶点A,B在数轴上,BC=1.6,点A对应的数为-1,则点B所对应的数为 W.
8 (1) 分别指出如图所示的数轴上A,B,C,D,E各点表示的有理数;
(2) 画出数轴并将下列各数标在数轴上:-2.5,,3,0.
建议用时:20+5分钟
9 (2025南通模拟)在数轴上,把表示-2的点沿着数轴移动7个单位长度得到的点所表示的数是( )
A. 5 B. -9 C. ±5 D. 5或-9
10 已知数轴上的点A到原点的距离为3,则数轴上到点A的距离是5的点所表示的数有( )
A. 1个 B. 2个 C. 3个 D. 4个
11 (2025扬州期末)如图,周长为6个单位长度的圆上的六等分点分别为A,B,C,D,E,F,点A落在1的位置.如果将圆在数轴上沿负方向连续滚动,那么落在数轴上-2 025的点是点( )
A. B B. C C. D D. E
(第11题) (第12题)
12 如图,将一刻度尺放在数轴上(数轴的单位长度是1 cm),刻度尺上“0 cm”和“3 cm”分别对应数轴上的3和0,那么刻度尺上“2.1 cm”对应数轴上的数为 .
13 (2024淮安涟水期中)数轴上的点A,B,C分别表示-3,-1.5,4.若把数轴的原点取在点B处,其余都不变,则点A表示的数变为 .
14 (2024淮安期中)如果将点B先向右移动4个单位长度,再向左移动6个单位长度后,这时点B表示的数是-6,则点B最初在数轴上表示的数为 .
15 已知在纸面上有一数轴(如图),折叠纸面:
(1) 若数1表示的点与数-1表示的点重合,则数-2表示的点与数 表示的点重合;
(2) 若数-1表示的点与数5表示的点重合,回答以下问题:
①数6表示的点与数 表示的点重合;
②若数轴上A,B两点之间的距离为11(点A在点B的左侧),且A,B两点经折叠后重合,求A,B两点表示的数是多少?
第2课时 有理数的大小
1. 会利用数轴比较有理数的大小,能正确地使用“>”或“<”连接.
2. 能初步进行有理数大小比较的推理和书写.
3. 能借助数轴解决数学中的问题,感受数形结合的思想,发展抽象能力和几何直观.
建议用时:15分钟
1 (2024甘肃)下列各数中,比-2小的数是( )
A. -1 B. -4 C. 4 D. 1
2 (2024广州)在四个数-10,-1,0,10中,最小的数是( )
A. -10 B. -1 C. 0 D. 10
3 (2024广安)下列各数中,最大的是( )
A. -2 B. - C. 0 D. 1
4 有理数m,n在数轴上的位置如图,则下列结论中正确的是( )
A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0
5 (2024辽宁)亚洲、欧洲、非洲和南美洲的最低海拔如表:
大洲 亚洲 欧洲 非洲 南美洲
最低海拔/m -415 -28 -156 -40
其中最低海拔最小的大洲是( )
A. 亚洲 B. 欧洲 C. 非洲 D. 南美洲
6 据中央气象台某天的预报,下列四个城市的最低气温分别是哈尔滨-11 ℃,杭州6 ℃,兰州 -5 ℃,海口27 ℃.其中,最低气温最高的城市为 ,最低气温最低的城市为 .
7 比较大小:- -.(填“>”“<”或“=”)
8 (2024南通海安月考)数轴上点A,B,C的位置如图所示.请回答下列问题:
(1) 表示有理数-3的点是点 ,将点C向左移动4个单位长度得到点C′,则点C′表示的有理数是 ;
(2) 在数轴上标出点D,E,其中点D,E分别表示有理数-和1.5;
(3) 将-3,0,-,1.5这四个数用“<”号连接的结果是 .
建议用时:20+5分钟
9 (2024连云港海州开学考试)小于-22且大于-24的整数为( )
A. -19 B. -23 C. -31 D. -22.1
10 下列比较两个数的大小中,正确的是( )
A. 1<-2 B. -<- C. 0<-0.1 D. -<-
11 从数轴上看,0是( )
A. 最小的整数 B. 最大的负数 C. 最小的有理数 D. 最小的非负数
12 (2024南京建邺月考)若在-0.154 8中用数字3替换其中的一个非零数字后,使所得的数最大,则被替换的数字是( )
A. 1 B. 5 C. 4 D. 8
13 (2024泰兴期中)关于有理数a,b,2,下列说法中正确的是( )
A. 如果a>2,a>b,那么b<2 B. 如果b<2,a>b,那么a>2
C. 如果a>2,b<2,那么a14 在-π,-1,-2,0中,比-3小的数是 .
15 比较大小:(1) - -;(2) - -π.(填“<”“>”或“=”)
16 (1) 最小的正整数是 ;(2) 最大的负整数是 .
17 (2025南通崇川期末)定义:[x]表示不大于x的最大整数.例如[1.6]=1,[π]= ,[-2.82]= .
18 写出符合条件的数,并将它们在数轴上表示出来:
(1) 大于-5且不大于-1的负整数;
(2) 大于-1的非正整数.
19 已知在数轴上有A,B,C三个点,点A表示的数是-4,点B表示的数是-2,点C表示的数是2.
(1) 在数轴上将A,B,C三点表示出来,并比较各数的大小(用“<”号连接);
(2) 如何移动点B,使它到点A和点C的距离相等.
2.2 数 轴
第1课时 数轴的概念
1. D 2. B 3. D 4. 4 5. B 6. π 7. 4
8. (1) 点A表示-4,点B表示-1,点C表示,
点D表示3,点E表示4.
(2) 如图所示:
9. D 10. D 11. D 12. 0.9 13. -1.5 14. -4
15. (1) 2
(2) ①-2
②因为A,B两点之间的距离为11,经折叠后重合,
所以点A,B距离对称中心的距离为11÷2=5.5.
由题意,得两点关于数2表示的点对称,点A在点B的左侧,
所以点B表示的数为2+5.5=7.5,点A表示的数为2-5.5=-3.5.
第2课时 有理数的大小
1. B 2. A 3. D 4. B 5. A 6. 海口 哈尔滨 7. <
8. (1) A -2
(2) 如图:
所以点D,E即为所求.
(3) -3<-<0<1.5
9. B 10. D 11. D 12. B 13. D 14. -π
15. (1) > (2) < 16. (1) 1 (2) -1 17. 3 -3
18. (1) -4,-3,-2,-1.
在数轴上的位置如图所示:
(2) -1,0.
在数轴上的位置如图所示:
19. (1) 在数轴上的位置如图所示:
根据数轴可知-4<-2<2.
(2) 点B向右移动一个单位长度,可得到它到点A和点C的距离相等.
同课章节目录
