2.4 有理数的加法与减法 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 2.4 有理数的加法与减法 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 955.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 19:00:11 | ||
图片预览




文档简介
2.4 有理数的加法与减法
第1课时 有理数的加法
1. 理解有理数的加法法则.
2. 熟练运用有理数的加法法则进行运算.
建议用时:15分钟
1 计算:(-3)+(-2)等于( )
A. -5 B. -1 C. 5 D. 1
2 (2024南通如皋月考)比-1大3的数是( )
A. -1 B. 0 C. 1 D. 2
3 (2024徐州丰县期中)甲地的平均海拔为-12 m,乙地平均海拔比甲地高50 m,则乙地的平均海拔为( )
A. -50 m B. 38 m C. -38 m D. 19 m
4 (2024宿迁宿城期中)如图,在数轴上方有一块黑色纸条,被遮掩的整数之和是( )
A. 1 B. -1 C. 2 D. -2
5 填空:
(1) +(-3)=-8; (2) +(-3)=8;
(3) (-3)+ =-1; (4) (-3)+ =0.
6 (2024苏州月考)已知a,b互为相反数,则a+6+b= .
7 (2024南京六合模拟)绝对值小于4的所有整数的和是 .
8 的相反数与的绝对值的和是 .
9 计算:
(1) (-0.9)+(-2.7); (2) 3.8+(-8.4); (3) 7+(-3.04);
(4) (-2.9)+(-0.31); (5) (-9.18)+6.18; (6) 4.23+(-6.77).
建议用时:20+5分钟
10 (2024泰州靖江月考)下列判断:①两个有理数相加,它们的和一定大于每一个加数;②一个正数与一个负数相加一定等于0;③两个负数的和的绝对值一定等于它们的绝对值的和;④两个正数的和一定是正数.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
11 如果a<0,b<0,且|a|>|b|,那么a+(-b)的值一定是( )
A. 正数 B. 负数 C. 0 D. 不确定
12 已知一个数为-5,另一个数比这个数的相反数大4,则这两个数的和为 .
13 已知|a|=2,|b|=3,且a+b<0,则a+b的值为 .
14 (2024苏州昆山期中)小明做了一道计算题:|(-3)+●|= ,其中“●”表示被墨水污染看不到的一个数,他翻看了答案得知该题的计算结果为6,那么“●”表示的数是 .
15 (2024南通期中)某学校深入开展足球进校园活动,为了提高足球运动员快速转身抢断能力,体育老师设计了折返跑训练.在足球场上画一条东西方向的直线,如果约定向东为正,向西为负,一运动员折返跑训练的记录如下(单位:m):
+15,-19,+16,-18,+21,-30,+35,-25,+25,-10.请解答下列问题:
(1) 该运动员最后到达的地方在出发点的哪个方向?距出发点多远?
(2) 该运动员本次训练结束,共跑了多少米?
16 已知|m|=3,|n|=5,且m<n,求m+n的值.
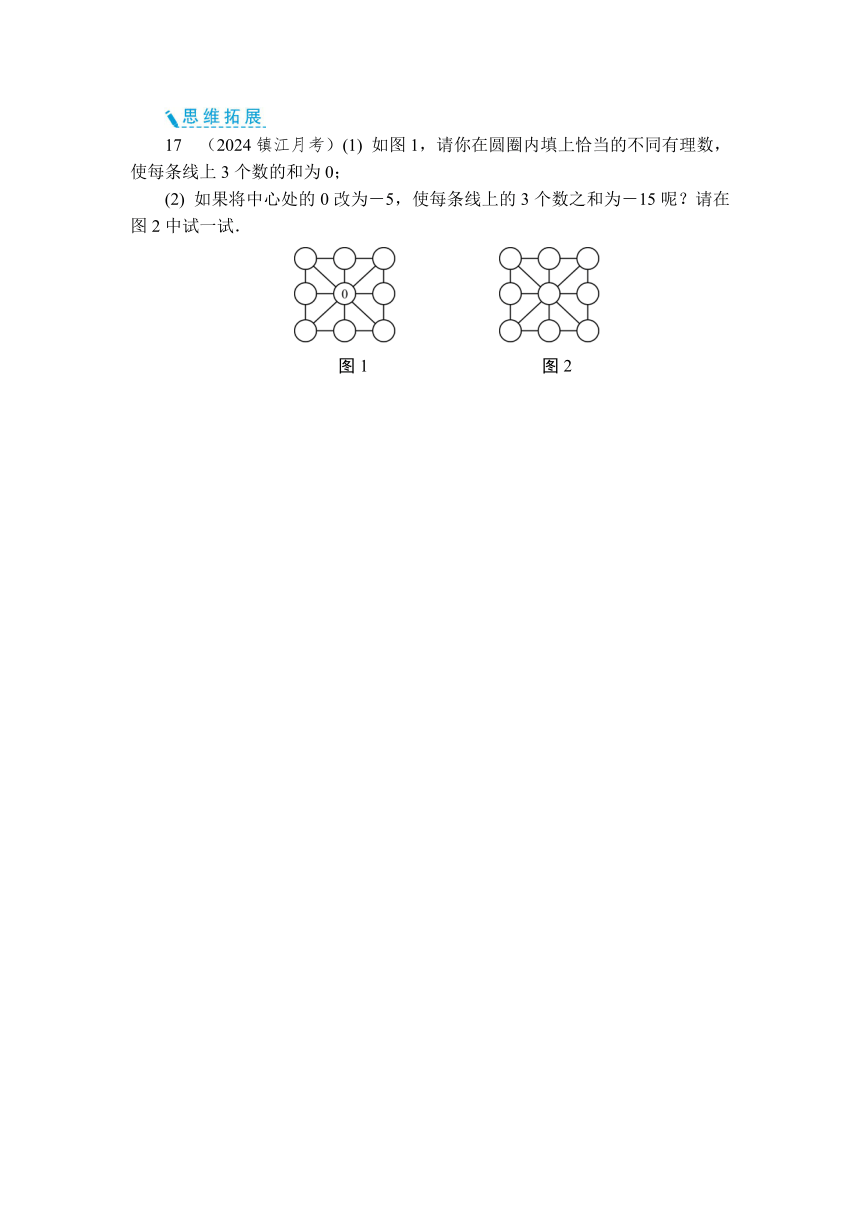
17 (2024镇江月考)(1) 如图1,请你在圆圈内填上恰当的不同有理数,使每条线上3个数的和为0;
(2) 如果将中心处的0改为-5,使每条线上的3个数之和为-15呢?请在图2中试一试.
图1 图2
第2课时 有理数加法运算律
1. 理解有理数的加法交换律与结合律.
2. 能灵活运用有理数的加法运算律进行简便计算.
建议用时:15分钟
1 小华计划每天背诵6个成语.将超过的个数记为正数,不足的个数记为负数,连续5天的背诵个数记录如下:+4,0,+5,-3,+2,则这5天他共背诵成语的个数为( )
A. 38 B. 36 C. 34 D. 30
2 计算43+(-78)+27+(-52)时,运算律用得最为恰当的是( )
A. [43+(-78)]+[27+(-52)] B. (43+27)+[(-78)+(-52)]
C. [43+(-52)]+[27+(-78)] D. [27+(-78)]+[43-(-52)]
3 下列变形中,运用加法运算律错误的是( )
A. (-8)+(-9)=(-9)+(-8) B. 4+(-6)+3=(-6)+4+3
C. [5+(-2)]+4=[5+(-4)]+2 D. +(-1)+(+)=(+)+(-1)
4 计算(-2.48)+4.33+(-7.52)+(-4.33)的结果为 .
5 (2024无锡梁溪月考)比-3大且比2小的所有整数的和为 .
6 计算:
(1) 23+(-17)+6+(-22); (2) 0.36+(-7.4)+0.5+(-0.6)+0.14;
(3) +++; (4) 5++4+.
建议用时:20+5分钟
7 给出下面的计算:-+3.2++7.8=-++3.2+7.8=[-+]+(3.2+7.8)=-1+11=10.其中,运用到的加法运算律表述最准确的是( )
A. 交换律 B. 结合律
C. 先用交换律,再用结合律 D. 先用结合律,再用交换律
8 当x=3,y=-,z=-(+2.25)时,(-x)+(-y)+z的值为 .
9 (2024苏州相城期中)如图,将-3,-2,-1,0,1,2,3,4,5分别填入九个空格内,使每行、每列、每条对角线上的三个数之和相等,现在a,b,c分别表示其中的一个数,则a-b+c的值为 .
4 a 2
-1 1 3
b 5 c
(第9题) (第10题)
10 如图,从左到右,在每个小格子中都填入一个整数,使其中任意三个相邻格中所填整数之和都相等,则c= ,第200个格子中的数为 .
11 一只蚂蚁从点O出发,在一条直线上来回爬行.假定把向右爬行的路程记为正数,向左爬行的路程记为负数,则蚂蚁爬过的各段路程依次为(单位: cm):
+5,-3,+10,-8,-6,+12,-10.
(1) 蚂蚁最后是否回到了出发点O
(2) 求蚂蚁与出发点O之间的最远距离;
(3) 在爬行过程中,如果每爬行1 cm奖励一颗糖,那么蚂蚁一共可以得到多少颗糖?
12 (2024连云港灌云月考)阅读下题的计算方法:
计算:-5+(-9)+17+(-3).
解:原式=[(-5)+(-)]+[(-9)+(-)]+(17+)+[(-3)+(-)]=[(-5)+(-9)+17+(-3)]+[(-)+(-)++(-)]=0+(-)=-.
上面这种计算方法叫作折项法,请按此方法计算:(-55)+(-44)+100+(-1).
第3课时 有理数的减法
1. 能够将有理数的减法运算转化为加法运算,初步掌握转化的思想.
2. 能熟练地进行有理数的减法运算.
建议用时:15分钟
1 (2025无锡一模)计算3-(-2)的结果等于( )
A. -1 B. 1 C. 3 D. 5
2 (2024长沙)“玉兔号”是我国首辆月球车,它和着陆器共同组成“嫦娥三号”探测器.“玉兔号”月球车能够耐受月球表面的最低温度是-180 ℃、最高温度是150 ℃,则它能够耐受的温差是( )
A. -180 ℃ B. 150 ℃ C. 30 ℃ D. 330 ℃
3 某超市出售的大米袋上,标有质量为(60±0.4) kg的字样,任意拿出两袋大米,它们的质量最多相差( )
A. 0.5 kg B. 0.6 kg C. 0.8 kg D. 0.95 kg
4 (2024连云港月考)比-3 ℃低7 ℃的温度是 ℃.
5 -8比 大4.
6 计算:
(1) (-37)-14; (2) -8-(-4); (3) (-98)-(-45);
(4) 3-5; (5) 0-; (6) -.
7 列式并计算:
(1) 和是-2,一个加数是6,求另一个加数;
(2) 差是-5,被减数是-7,求减数;
(3) 一个数是16,另一个数比16的相反数小-2,求这两个数的差.
建议用时:20+5分钟
8 如图,数轴上A,B两点表示的数分别是a,b,则计算|b|-|a|正确的是( )
A. b-a B. a-b C. a+b D. -a-b
9 有理数a,b在数轴上对应的点的位置如图,用“>”“<”或“=”填空.
(1) a+b 0; (2) (-a)+(-b) 0;
(3) a-b 0; (4) (-a)-(-b) 0.
10 (2024南通海安月考)小华做这样一道题“计算|(-4)-*|”,其中*表示被墨水染黑看不清的一个数,他翻开后面的答案得知该题的结果为7,那么*表示的数是 .
11 (2024无锡宜兴期中)已知|x|=5,|y|=3,且|x-y|=y-x,则x+y= .
12 (2024扬州月考)某同学在计算-3-N时,误将-N看成了+N,从而算得结果是5,请你算出正确结果 .
13 (2024扬州广陵月考)现定义某种新运算:对任意两个有理数a,b,有a※b=|a|-b.如:2※3=|2|-3=-1,(a+1)※4=|a+1|-4.
(1) 计算:(-3)※(-2);
(2) 计算:[(-4)※5]※2.
14 点A,B在数轴上分别表示有理数a,b,则A,B两点之间的距离表示为AB=|a-b|,或AB=|b-a|.例:如图1,点A表示的数a=-3,点B表示的数b=-1,则AB=|a-b|=|-3-(-1)|=|-3+1|=|-2|=2,或AB=|b-a|=|-1-(-3)|=|-1+3|=|2|=2.
利用数形结合思想回答下列问题:
(1) 数轴上表示2和-1的两点之间的距离为 ;
(2) 数轴上表示x和-1的两点之间的距离为 ;若x表示一个有理数,且-4(3) 如图2,数轴上从左到右的三个点A,B,C所对应的数分别为a,b,c.其中AB=2 020,BC=1 000.
①若以B为原点,直接写出点A,C所对应的数,并计算a+b+c的值;
②若O是原点,点B在原点的右侧,且OB=18,求a+b+c的值.
图1 图2
第4课时 有理数的加减混合运算
1. 熟练地进行有理数的加减混合运算,并能解决实际问题.
2. 能够灵活运用运算律进行巧算.
建议用时:15分钟
1 (2024苏州吴江月考)把7-(-3)+(-5)-(+2)写成省略加号的和的形式为( )
A. 7+3-5-2 B. 7-3-5-2 C. 7+3+5-2 D. 7+3-5+2
2 对式子“-7+10-8-2”的读法中,正确的是( )
A. 负7加10减8减2 B. 负7正10负8减2
C. 负7,加10,负8,负2的和 D. 减7加10减8减2
3 某公交车原坐有22人,经过4个站点时上、下车的人数情况如下(上车为正,下车为负):(+4,-2),(+6,-5),(+2,-3),(+1,-7),则车上还有( )
A. 14人 B. 18人 C. 24人 D. 26人
4 把(-)-(-)+(-)-(+)统一为加法运算为: .
5 (2025南京鼓楼期末)紫金山山顶的气温某天早晨是零下2 ℃,中午上升了4 ℃,傍晚下降了6 ℃,这天傍晚紫金山山顶的气温是 ℃.
6 计算:
(1) -7-|-9|-(-11)-3; (2) 5.6+(-0.9)+4.4+(-8.1);
(3) ++; (4) ---(-2.75).
7 (2024常州天宁月考)在抗洪抢险中,人民解放军的冲锋舟沿东西方向的河流抢救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行情况记录如下(单位:km):10,-9,-5,+7,-11,+2,-10,+6.
(1) B地在A地哪个方向,距离为多少?
(2) 若冲锋舟每千米耗油0.5 L,出发时油箱有油25 L,求途中至少还需补充多少升油?
建议用时:20+5分钟
8 下列计算中,结果等于5的是( )
A. (-9)+(-4) B. -(-3.6)+(-8)-(-9)
C. 21-(+16)+(-1) D. (-3.3)-+|-3.3|+1
9 -3,7,-14的和比它们的绝对值的和小( )
A. -34 B. -10 C. 10 D. 34
10 计算:1-(+2)+3-(+4)+5-(+6)+…-(+2 024)= .
11 (2024无锡江阴月考)若规定图形表示运算a-b+c,图形表示运算x+z-y-w,则+= .
12 在一次考试中,某班14名同学的成绩如下(单位:分):79,81,95,92,68,75,80,93,85,65,72,75,80,87.
(1) 以80分为标准,成绩高于80分的记为正数,低于80分的记为负数.请你按上述要求表示出这14名同学的成绩;
(2) 用(1)中的成绩求他们的平均成绩.
13 观察下面一组等式:
|2-1|=2-1=1,|1-2|=2-1=1;
|(-2)-(-5)|=(-2)-(-5)=3,|(-5)-(-2)|=(-2)-(-5)=3;
|6.4-(-3.5)|=6.4-(-3.5)=9.9,|(-3.5)-6.4|=6.4-(-3.5)=9.9.
解决下列问题:
(1) 化简|(-2)-1|;
(2) 化简|3.14-π|的结果是 ;
(3) 求+++…+的值.
2.4 有理数的加法与减法
第1课时 有理数的加法
1. A 2. D 3. B 4. D
5. (1) -5 (2) 11 (3) 2 (4) 3
6. 6 7. 0 8. -
9. (1) -3.6 (2) -4.6 (3) 3.96 (4) -3.21 (5) -3 (6) -2.54
10. C 11. B 12. 4 13. -5或-1
14. 9或-3
15. (1) 15+(-19)+16+(-18)+21+(-30)+35+(-25)+25+(-10)=10(m),
故最后到达的地方在出发点的东边,距出发点10 m.
(2) |+15|+|-19|+|+16|+|-18|+|+21|+|-30|+|+35|+|-25|+|+25|+|-10|
=15+19+16+18+21+30+35+25+25+10
=214(m),
故该运动员本次训练结束,共跑了214 m.
16. 因为|m|=3,|n|=5,且m<n,
所以m=3,n=5或m=-3,n=5,
则m+n的值为8或2.
17. 如图所示,答案不唯一.
图1 图2
第2课时 有理数加法运算律
1. A 2. B 3. C 4. -10 5. -3
6. (1) -10 (2) -7 (3) -1 (4) 4
7. C 8. 3 9. -5 10. 3 -1
11. (1) 因为(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)=0(cm),
所以蚂蚁最后回到了出发点O.
(2) 根据记录,蚂蚁与出发点O之间的距离分别为5 cm,2 cm,12 cm,4 cm,2 cm,10 cm,0 cm,
所以蚂蚁与出发点O之间的最远距离是12 cm.
(3) |+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|=54(cm),54×1=54(颗),
所以蚂蚁一共可以得到54颗糖.
12. 原式=-55--44-+100+-1-
=(-55-44-1+100)+(---+)
=0+(-1)
=-1.
第3课时 有理数的减法
1. D 2. D 3. C 4. -10 5. -12
6. (1) -51 (2) -4 (3) -53 (4) -2 (5) 7 (6) -
7. (1) -2-6=-8.
(2) -7-(-5)=-7+5=-2.
(3) 16-[-16-(-2)]=16-(-14)=16+14=30或[-16-(-2)]-16=-14-16=-30.
8. C
9. (1) < (2) > (3) < (4) >
10. -11或3 11. -8或-2 12. -12
13. (1) 原式=|-3|-(-2)=3+2=5.
(2) 原式=(|-4|-5)※2=(-1)※2=|-1|-2=-1.
14. (1) 3
(2) 6
(3) ①以B为原点,则点A表示的数为-2 020,
点C表示的数为+1 000,即a=-2 020,b=0,
c=+1 000,
所以a+b+c=-2 020+0+(+1 000)=-1 020.
②O是原点,点B在原点的右侧,且OB=18,则点B表示的数为+18,点C表示的数为+1 018,点A表示的数为-2 002,即a=-2 002,b=+18,c=+1 018,
所以a+b+c=-2 002+(+18)+(+1 018)=-966.
第4课时 有理数的加减混合运算
1. A 2. A 3. B 4. -+-- 5. -4
6. (1) -8 (2) 1 (3) (4) -0.6
7. (1) 10-9-5+7-11+2-10+6=-10,
所以B地在A地的西方,距离10 km处.
(2) (10+9+5+7+11+2+10+6)×0.5-25=5(L).
故至少还需补充5 L油.
8. B 9. D 10. -1 012 11. 0
12. (1) -1分,+1分,+15分,+12分,-12分,-5分,0分,+13分,+5分,-15分,-8分,-5分,0分,+7分.
(2) [-1+(+1)+(+15)+(+12)+(-12)+(-5)+0+(+13)+(+5)+(-15)+(-8)+(-5)+0+(+7)]÷14=0.5(分),80+0.5=80.5(分),所以他们的平均成绩为80.5分.
13. (1) 根据题意,得|(-2)-1|=1-(-2)=3.
(2) π-3.14
(3) 原式=-+-+-+…+-=-=.
第1课时 有理数的加法
1. 理解有理数的加法法则.
2. 熟练运用有理数的加法法则进行运算.
建议用时:15分钟
1 计算:(-3)+(-2)等于( )
A. -5 B. -1 C. 5 D. 1
2 (2024南通如皋月考)比-1大3的数是( )
A. -1 B. 0 C. 1 D. 2
3 (2024徐州丰县期中)甲地的平均海拔为-12 m,乙地平均海拔比甲地高50 m,则乙地的平均海拔为( )
A. -50 m B. 38 m C. -38 m D. 19 m
4 (2024宿迁宿城期中)如图,在数轴上方有一块黑色纸条,被遮掩的整数之和是( )
A. 1 B. -1 C. 2 D. -2
5 填空:
(1) +(-3)=-8; (2) +(-3)=8;
(3) (-3)+ =-1; (4) (-3)+ =0.
6 (2024苏州月考)已知a,b互为相反数,则a+6+b= .
7 (2024南京六合模拟)绝对值小于4的所有整数的和是 .
8 的相反数与的绝对值的和是 .
9 计算:
(1) (-0.9)+(-2.7); (2) 3.8+(-8.4); (3) 7+(-3.04);
(4) (-2.9)+(-0.31); (5) (-9.18)+6.18; (6) 4.23+(-6.77).
建议用时:20+5分钟
10 (2024泰州靖江月考)下列判断:①两个有理数相加,它们的和一定大于每一个加数;②一个正数与一个负数相加一定等于0;③两个负数的和的绝对值一定等于它们的绝对值的和;④两个正数的和一定是正数.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
11 如果a<0,b<0,且|a|>|b|,那么a+(-b)的值一定是( )
A. 正数 B. 负数 C. 0 D. 不确定
12 已知一个数为-5,另一个数比这个数的相反数大4,则这两个数的和为 .
13 已知|a|=2,|b|=3,且a+b<0,则a+b的值为 .
14 (2024苏州昆山期中)小明做了一道计算题:|(-3)+●|= ,其中“●”表示被墨水污染看不到的一个数,他翻看了答案得知该题的计算结果为6,那么“●”表示的数是 .
15 (2024南通期中)某学校深入开展足球进校园活动,为了提高足球运动员快速转身抢断能力,体育老师设计了折返跑训练.在足球场上画一条东西方向的直线,如果约定向东为正,向西为负,一运动员折返跑训练的记录如下(单位:m):
+15,-19,+16,-18,+21,-30,+35,-25,+25,-10.请解答下列问题:
(1) 该运动员最后到达的地方在出发点的哪个方向?距出发点多远?
(2) 该运动员本次训练结束,共跑了多少米?
16 已知|m|=3,|n|=5,且m<n,求m+n的值.
17 (2024镇江月考)(1) 如图1,请你在圆圈内填上恰当的不同有理数,使每条线上3个数的和为0;
(2) 如果将中心处的0改为-5,使每条线上的3个数之和为-15呢?请在图2中试一试.
图1 图2
第2课时 有理数加法运算律
1. 理解有理数的加法交换律与结合律.
2. 能灵活运用有理数的加法运算律进行简便计算.
建议用时:15分钟
1 小华计划每天背诵6个成语.将超过的个数记为正数,不足的个数记为负数,连续5天的背诵个数记录如下:+4,0,+5,-3,+2,则这5天他共背诵成语的个数为( )
A. 38 B. 36 C. 34 D. 30
2 计算43+(-78)+27+(-52)时,运算律用得最为恰当的是( )
A. [43+(-78)]+[27+(-52)] B. (43+27)+[(-78)+(-52)]
C. [43+(-52)]+[27+(-78)] D. [27+(-78)]+[43-(-52)]
3 下列变形中,运用加法运算律错误的是( )
A. (-8)+(-9)=(-9)+(-8) B. 4+(-6)+3=(-6)+4+3
C. [5+(-2)]+4=[5+(-4)]+2 D. +(-1)+(+)=(+)+(-1)
4 计算(-2.48)+4.33+(-7.52)+(-4.33)的结果为 .
5 (2024无锡梁溪月考)比-3大且比2小的所有整数的和为 .
6 计算:
(1) 23+(-17)+6+(-22); (2) 0.36+(-7.4)+0.5+(-0.6)+0.14;
(3) +++; (4) 5++4+.
建议用时:20+5分钟
7 给出下面的计算:-+3.2++7.8=-++3.2+7.8=[-+]+(3.2+7.8)=-1+11=10.其中,运用到的加法运算律表述最准确的是( )
A. 交换律 B. 结合律
C. 先用交换律,再用结合律 D. 先用结合律,再用交换律
8 当x=3,y=-,z=-(+2.25)时,(-x)+(-y)+z的值为 .
9 (2024苏州相城期中)如图,将-3,-2,-1,0,1,2,3,4,5分别填入九个空格内,使每行、每列、每条对角线上的三个数之和相等,现在a,b,c分别表示其中的一个数,则a-b+c的值为 .
4 a 2
-1 1 3
b 5 c
(第9题) (第10题)
10 如图,从左到右,在每个小格子中都填入一个整数,使其中任意三个相邻格中所填整数之和都相等,则c= ,第200个格子中的数为 .
11 一只蚂蚁从点O出发,在一条直线上来回爬行.假定把向右爬行的路程记为正数,向左爬行的路程记为负数,则蚂蚁爬过的各段路程依次为(单位: cm):
+5,-3,+10,-8,-6,+12,-10.
(1) 蚂蚁最后是否回到了出发点O
(2) 求蚂蚁与出发点O之间的最远距离;
(3) 在爬行过程中,如果每爬行1 cm奖励一颗糖,那么蚂蚁一共可以得到多少颗糖?
12 (2024连云港灌云月考)阅读下题的计算方法:
计算:-5+(-9)+17+(-3).
解:原式=[(-5)+(-)]+[(-9)+(-)]+(17+)+[(-3)+(-)]=[(-5)+(-9)+17+(-3)]+[(-)+(-)++(-)]=0+(-)=-.
上面这种计算方法叫作折项法,请按此方法计算:(-55)+(-44)+100+(-1).
第3课时 有理数的减法
1. 能够将有理数的减法运算转化为加法运算,初步掌握转化的思想.
2. 能熟练地进行有理数的减法运算.
建议用时:15分钟
1 (2025无锡一模)计算3-(-2)的结果等于( )
A. -1 B. 1 C. 3 D. 5
2 (2024长沙)“玉兔号”是我国首辆月球车,它和着陆器共同组成“嫦娥三号”探测器.“玉兔号”月球车能够耐受月球表面的最低温度是-180 ℃、最高温度是150 ℃,则它能够耐受的温差是( )
A. -180 ℃ B. 150 ℃ C. 30 ℃ D. 330 ℃
3 某超市出售的大米袋上,标有质量为(60±0.4) kg的字样,任意拿出两袋大米,它们的质量最多相差( )
A. 0.5 kg B. 0.6 kg C. 0.8 kg D. 0.95 kg
4 (2024连云港月考)比-3 ℃低7 ℃的温度是 ℃.
5 -8比 大4.
6 计算:
(1) (-37)-14; (2) -8-(-4); (3) (-98)-(-45);
(4) 3-5; (5) 0-; (6) -.
7 列式并计算:
(1) 和是-2,一个加数是6,求另一个加数;
(2) 差是-5,被减数是-7,求减数;
(3) 一个数是16,另一个数比16的相反数小-2,求这两个数的差.
建议用时:20+5分钟
8 如图,数轴上A,B两点表示的数分别是a,b,则计算|b|-|a|正确的是( )
A. b-a B. a-b C. a+b D. -a-b
9 有理数a,b在数轴上对应的点的位置如图,用“>”“<”或“=”填空.
(1) a+b 0; (2) (-a)+(-b) 0;
(3) a-b 0; (4) (-a)-(-b) 0.
10 (2024南通海安月考)小华做这样一道题“计算|(-4)-*|”,其中*表示被墨水染黑看不清的一个数,他翻开后面的答案得知该题的结果为7,那么*表示的数是 .
11 (2024无锡宜兴期中)已知|x|=5,|y|=3,且|x-y|=y-x,则x+y= .
12 (2024扬州月考)某同学在计算-3-N时,误将-N看成了+N,从而算得结果是5,请你算出正确结果 .
13 (2024扬州广陵月考)现定义某种新运算:对任意两个有理数a,b,有a※b=|a|-b.如:2※3=|2|-3=-1,(a+1)※4=|a+1|-4.
(1) 计算:(-3)※(-2);
(2) 计算:[(-4)※5]※2.
14 点A,B在数轴上分别表示有理数a,b,则A,B两点之间的距离表示为AB=|a-b|,或AB=|b-a|.例:如图1,点A表示的数a=-3,点B表示的数b=-1,则AB=|a-b|=|-3-(-1)|=|-3+1|=|-2|=2,或AB=|b-a|=|-1-(-3)|=|-1+3|=|2|=2.
利用数形结合思想回答下列问题:
(1) 数轴上表示2和-1的两点之间的距离为 ;
(2) 数轴上表示x和-1的两点之间的距离为 ;若x表示一个有理数,且-4
①若以B为原点,直接写出点A,C所对应的数,并计算a+b+c的值;
②若O是原点,点B在原点的右侧,且OB=18,求a+b+c的值.
图1 图2
第4课时 有理数的加减混合运算
1. 熟练地进行有理数的加减混合运算,并能解决实际问题.
2. 能够灵活运用运算律进行巧算.
建议用时:15分钟
1 (2024苏州吴江月考)把7-(-3)+(-5)-(+2)写成省略加号的和的形式为( )
A. 7+3-5-2 B. 7-3-5-2 C. 7+3+5-2 D. 7+3-5+2
2 对式子“-7+10-8-2”的读法中,正确的是( )
A. 负7加10减8减2 B. 负7正10负8减2
C. 负7,加10,负8,负2的和 D. 减7加10减8减2
3 某公交车原坐有22人,经过4个站点时上、下车的人数情况如下(上车为正,下车为负):(+4,-2),(+6,-5),(+2,-3),(+1,-7),则车上还有( )
A. 14人 B. 18人 C. 24人 D. 26人
4 把(-)-(-)+(-)-(+)统一为加法运算为: .
5 (2025南京鼓楼期末)紫金山山顶的气温某天早晨是零下2 ℃,中午上升了4 ℃,傍晚下降了6 ℃,这天傍晚紫金山山顶的气温是 ℃.
6 计算:
(1) -7-|-9|-(-11)-3; (2) 5.6+(-0.9)+4.4+(-8.1);
(3) ++; (4) ---(-2.75).
7 (2024常州天宁月考)在抗洪抢险中,人民解放军的冲锋舟沿东西方向的河流抢救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行情况记录如下(单位:km):10,-9,-5,+7,-11,+2,-10,+6.
(1) B地在A地哪个方向,距离为多少?
(2) 若冲锋舟每千米耗油0.5 L,出发时油箱有油25 L,求途中至少还需补充多少升油?
建议用时:20+5分钟
8 下列计算中,结果等于5的是( )
A. (-9)+(-4) B. -(-3.6)+(-8)-(-9)
C. 21-(+16)+(-1) D. (-3.3)-+|-3.3|+1
9 -3,7,-14的和比它们的绝对值的和小( )
A. -34 B. -10 C. 10 D. 34
10 计算:1-(+2)+3-(+4)+5-(+6)+…-(+2 024)= .
11 (2024无锡江阴月考)若规定图形表示运算a-b+c,图形表示运算x+z-y-w,则+= .
12 在一次考试中,某班14名同学的成绩如下(单位:分):79,81,95,92,68,75,80,93,85,65,72,75,80,87.
(1) 以80分为标准,成绩高于80分的记为正数,低于80分的记为负数.请你按上述要求表示出这14名同学的成绩;
(2) 用(1)中的成绩求他们的平均成绩.
13 观察下面一组等式:
|2-1|=2-1=1,|1-2|=2-1=1;
|(-2)-(-5)|=(-2)-(-5)=3,|(-5)-(-2)|=(-2)-(-5)=3;
|6.4-(-3.5)|=6.4-(-3.5)=9.9,|(-3.5)-6.4|=6.4-(-3.5)=9.9.
解决下列问题:
(1) 化简|(-2)-1|;
(2) 化简|3.14-π|的结果是 ;
(3) 求+++…+的值.
2.4 有理数的加法与减法
第1课时 有理数的加法
1. A 2. D 3. B 4. D
5. (1) -5 (2) 11 (3) 2 (4) 3
6. 6 7. 0 8. -
9. (1) -3.6 (2) -4.6 (3) 3.96 (4) -3.21 (5) -3 (6) -2.54
10. C 11. B 12. 4 13. -5或-1
14. 9或-3
15. (1) 15+(-19)+16+(-18)+21+(-30)+35+(-25)+25+(-10)=10(m),
故最后到达的地方在出发点的东边,距出发点10 m.
(2) |+15|+|-19|+|+16|+|-18|+|+21|+|-30|+|+35|+|-25|+|+25|+|-10|
=15+19+16+18+21+30+35+25+25+10
=214(m),
故该运动员本次训练结束,共跑了214 m.
16. 因为|m|=3,|n|=5,且m<n,
所以m=3,n=5或m=-3,n=5,
则m+n的值为8或2.
17. 如图所示,答案不唯一.
图1 图2
第2课时 有理数加法运算律
1. A 2. B 3. C 4. -10 5. -3
6. (1) -10 (2) -7 (3) -1 (4) 4
7. C 8. 3 9. -5 10. 3 -1
11. (1) 因为(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)=0(cm),
所以蚂蚁最后回到了出发点O.
(2) 根据记录,蚂蚁与出发点O之间的距离分别为5 cm,2 cm,12 cm,4 cm,2 cm,10 cm,0 cm,
所以蚂蚁与出发点O之间的最远距离是12 cm.
(3) |+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|=54(cm),54×1=54(颗),
所以蚂蚁一共可以得到54颗糖.
12. 原式=-55--44-+100+-1-
=(-55-44-1+100)+(---+)
=0+(-1)
=-1.
第3课时 有理数的减法
1. D 2. D 3. C 4. -10 5. -12
6. (1) -51 (2) -4 (3) -53 (4) -2 (5) 7 (6) -
7. (1) -2-6=-8.
(2) -7-(-5)=-7+5=-2.
(3) 16-[-16-(-2)]=16-(-14)=16+14=30或[-16-(-2)]-16=-14-16=-30.
8. C
9. (1) < (2) > (3) < (4) >
10. -11或3 11. -8或-2 12. -12
13. (1) 原式=|-3|-(-2)=3+2=5.
(2) 原式=(|-4|-5)※2=(-1)※2=|-1|-2=-1.
14. (1) 3
(2) 6
(3) ①以B为原点,则点A表示的数为-2 020,
点C表示的数为+1 000,即a=-2 020,b=0,
c=+1 000,
所以a+b+c=-2 020+0+(+1 000)=-1 020.
②O是原点,点B在原点的右侧,且OB=18,则点B表示的数为+18,点C表示的数为+1 018,点A表示的数为-2 002,即a=-2 002,b=+18,c=+1 018,
所以a+b+c=-2 002+(+18)+(+1 018)=-966.
第4课时 有理数的加减混合运算
1. A 2. A 3. B 4. -+-- 5. -4
6. (1) -8 (2) 1 (3) (4) -0.6
7. (1) 10-9-5+7-11+2-10+6=-10,
所以B地在A地的西方,距离10 km处.
(2) (10+9+5+7+11+2+10+6)×0.5-25=5(L).
故至少还需补充5 L油.
8. B 9. D 10. -1 012 11. 0
12. (1) -1分,+1分,+15分,+12分,-12分,-5分,0分,+13分,+5分,-15分,-8分,-5分,0分,+7分.
(2) [-1+(+1)+(+15)+(+12)+(-12)+(-5)+0+(+13)+(+5)+(-15)+(-8)+(-5)+0+(+7)]÷14=0.5(分),80+0.5=80.5(分),所以他们的平均成绩为80.5分.
13. (1) 根据题意,得|(-2)-1|=1-(-2)=3.
(2) π-3.14
(3) 原式=-+-+-+…+-=-=.
同课章节目录
