3.1 字母表示数 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 3.1 字母表示数 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 906.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 19:04:32 | ||
图片预览

文档简介
3.1 字母表示数
1. 借助现实情境进一步理解用字母表示数的意义.
2. 会用字母表示简单问题中的性质、关系和规律.
建议用时:15分钟
1 小明买了m kg橘子,花了n元,则每千克橘子的价格是( )
A. 元 B. 元 C. mn元 D. (m-n)元
2 “m与n差的3倍”可表示为( )
A. m-n B. m-3n
C. 3(n-m) D. 3(m-n)
3 若有三个连续的偶数,最大的一个数是2n+2,则最小的一个数可以表示为( )
A. 2n-2 B. 2n
C. 2n+1 D. 2n-1
4 若一个两位数,个位数字为m,十位数字为n,则这个两位数用字母可以表示为( )
A. nm B. mn
C. 10m+n D. 10n+m
5 (2024徐州邳州期中)某种商品原价每件m元,先打6折(按原价的60%)出售,随后每件又降价8元,则此时的售价为 元.
6 (2025南通通州期末)棱长为a的正方体的体积为 .(用含有字母a的式子表示)
7 如图,表示图中最大的长方形与六个小长方形间面积关系的等式为 .
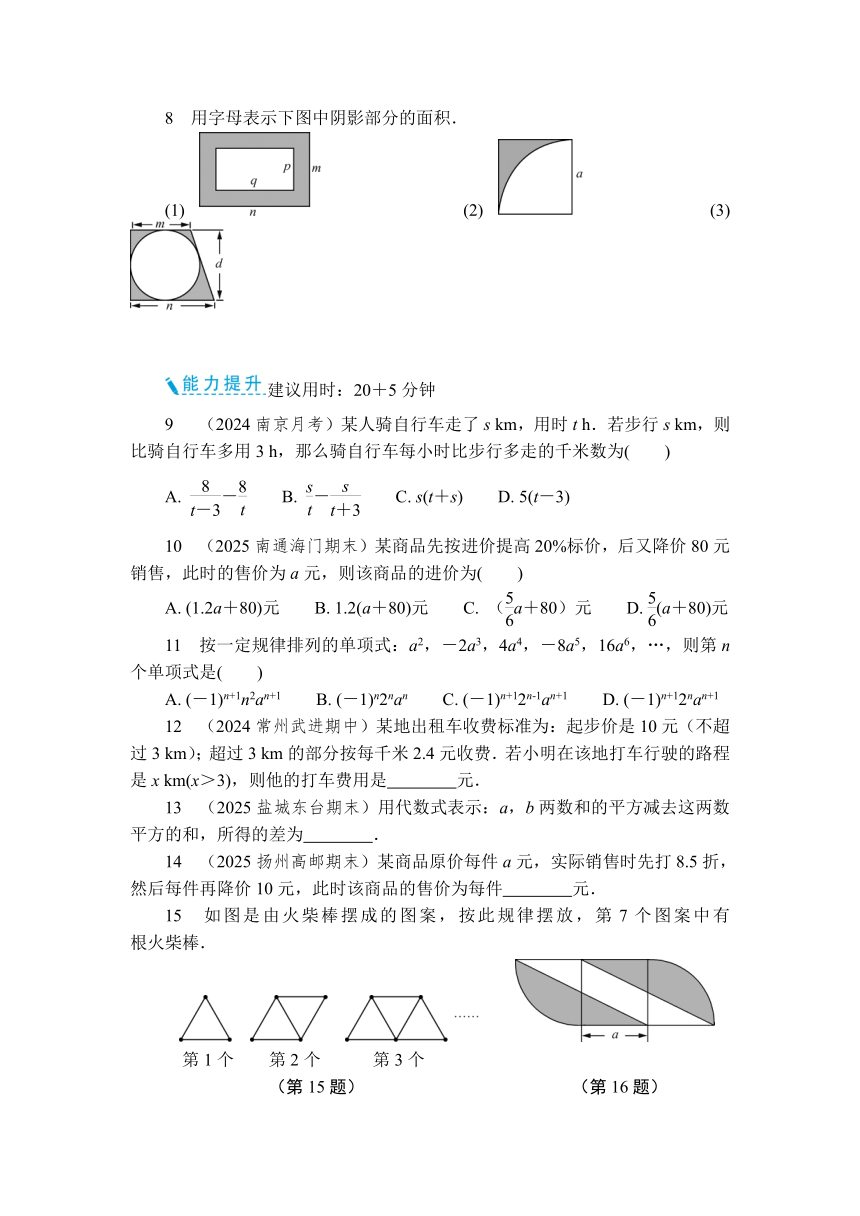
8 用字母表示下图中阴影部分的面积.
(1) (2) (3)
建议用时:20+5分钟
9 (2024南京月考)某人骑自行车走了s km,用时t h.若步行s km,则比骑自行车多用3 h,那么骑自行车每小时比步行多走的千米数为( )
A. - B. - C. s(t+s) D. 5(t-3)
10 (2025南通海门期末)某商品先按进价提高20%标价,后又降价80元销售,此时的售价为a元,则该商品的进价为( )
A. (1.2a+80)元 B. 1.2(a+80)元 C. (a+80)元 D. (a+80)元
11 按一定规律排列的单项式:a2,-2a3,4a4,-8a5,16a6,…,则第n个单项式是( )
A. (-1)n+1n2an+1 B. (-1)n2nan C. (-1)n+12n-1an+1 D. (-1)n+12nan+1
12 (2024常州武进期中)某地出租车收费标准为:起步价是10元(不超过3 km);超过3 km的部分按每千米2.4元收费.若小明在该地打车行驶的路程是x km(x>3),则他的打车费用是 元.
13 (2025盐城东台期末)用代数式表示:a,b两数和的平方减去这两数平方的和,所得的差为 .
14 (2025扬州高邮期末)某商品原价每件a元,实际销售时先打8.5折,然后每件再降价10元,此时该商品的售价为每件 元.
15 如图是由火柴棒摆成的图案,按此规律摆放,第7个图案中有 根火柴棒.
第1个 第2个 第3个
(第15题) (第16题)
16 如图,正方形的边长为a,以正方形的边长a为半径向外分别作两个四分之一圆,则阴影部分的面积可表示为 .(用含a的代数式表示,结果保留π)
17 将若干个棱长为a的正方体按如图所示的方式摆放在一起.
(1) 填表:
正方体的个数 1 2 3 4 5 …
图形的表面积…
(2) 照这样的规律摆下去,用n个这样的正方体摆成的图形的表面积是多少?
3.1 字母表示数
1. A 2. D 3. A 4. D 5. 0.6m-8 6. a3
7. (a+b)(2a+b)=2a2+3ab+b2
8. (1) mn-pq
(2) a2-πa2
(3) -2
9. B 10. D 11. C 12. 2.4x+2.8
13. (a+b)2-(a2+b2) 14. 0.85a-10 15. 15
16. πa2
17. (1) 6a2 10a2 14a2 18a2 22a2
(2) (2+4n)a2
1. 借助现实情境进一步理解用字母表示数的意义.
2. 会用字母表示简单问题中的性质、关系和规律.
建议用时:15分钟
1 小明买了m kg橘子,花了n元,则每千克橘子的价格是( )
A. 元 B. 元 C. mn元 D. (m-n)元
2 “m与n差的3倍”可表示为( )
A. m-n B. m-3n
C. 3(n-m) D. 3(m-n)
3 若有三个连续的偶数,最大的一个数是2n+2,则最小的一个数可以表示为( )
A. 2n-2 B. 2n
C. 2n+1 D. 2n-1
4 若一个两位数,个位数字为m,十位数字为n,则这个两位数用字母可以表示为( )
A. nm B. mn
C. 10m+n D. 10n+m
5 (2024徐州邳州期中)某种商品原价每件m元,先打6折(按原价的60%)出售,随后每件又降价8元,则此时的售价为 元.
6 (2025南通通州期末)棱长为a的正方体的体积为 .(用含有字母a的式子表示)
7 如图,表示图中最大的长方形与六个小长方形间面积关系的等式为 .
8 用字母表示下图中阴影部分的面积.
(1) (2) (3)
建议用时:20+5分钟
9 (2024南京月考)某人骑自行车走了s km,用时t h.若步行s km,则比骑自行车多用3 h,那么骑自行车每小时比步行多走的千米数为( )
A. - B. - C. s(t+s) D. 5(t-3)
10 (2025南通海门期末)某商品先按进价提高20%标价,后又降价80元销售,此时的售价为a元,则该商品的进价为( )
A. (1.2a+80)元 B. 1.2(a+80)元 C. (a+80)元 D. (a+80)元
11 按一定规律排列的单项式:a2,-2a3,4a4,-8a5,16a6,…,则第n个单项式是( )
A. (-1)n+1n2an+1 B. (-1)n2nan C. (-1)n+12n-1an+1 D. (-1)n+12nan+1
12 (2024常州武进期中)某地出租车收费标准为:起步价是10元(不超过3 km);超过3 km的部分按每千米2.4元收费.若小明在该地打车行驶的路程是x km(x>3),则他的打车费用是 元.
13 (2025盐城东台期末)用代数式表示:a,b两数和的平方减去这两数平方的和,所得的差为 .
14 (2025扬州高邮期末)某商品原价每件a元,实际销售时先打8.5折,然后每件再降价10元,此时该商品的售价为每件 元.
15 如图是由火柴棒摆成的图案,按此规律摆放,第7个图案中有 根火柴棒.
第1个 第2个 第3个
(第15题) (第16题)
16 如图,正方形的边长为a,以正方形的边长a为半径向外分别作两个四分之一圆,则阴影部分的面积可表示为 .(用含a的代数式表示,结果保留π)
17 将若干个棱长为a的正方体按如图所示的方式摆放在一起.
(1) 填表:
正方体的个数 1 2 3 4 5 …
图形的表面积…
(2) 照这样的规律摆下去,用n个这样的正方体摆成的图形的表面积是多少?
3.1 字母表示数
1. A 2. D 3. A 4. D 5. 0.6m-8 6. a3
7. (a+b)(2a+b)=2a2+3ab+b2
8. (1) mn-pq
(2) a2-πa2
(3) -2
9. B 10. D 11. C 12. 2.4x+2.8
13. (a+b)2-(a2+b2) 14. 0.85a-10 15. 15
16. πa2
17. (1) 6a2 10a2 14a2 18a2 22a2
(2) (2+4n)a2
同课章节目录
