6.1 直线、射线、线段 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 6.1 直线、射线、线段 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册 | 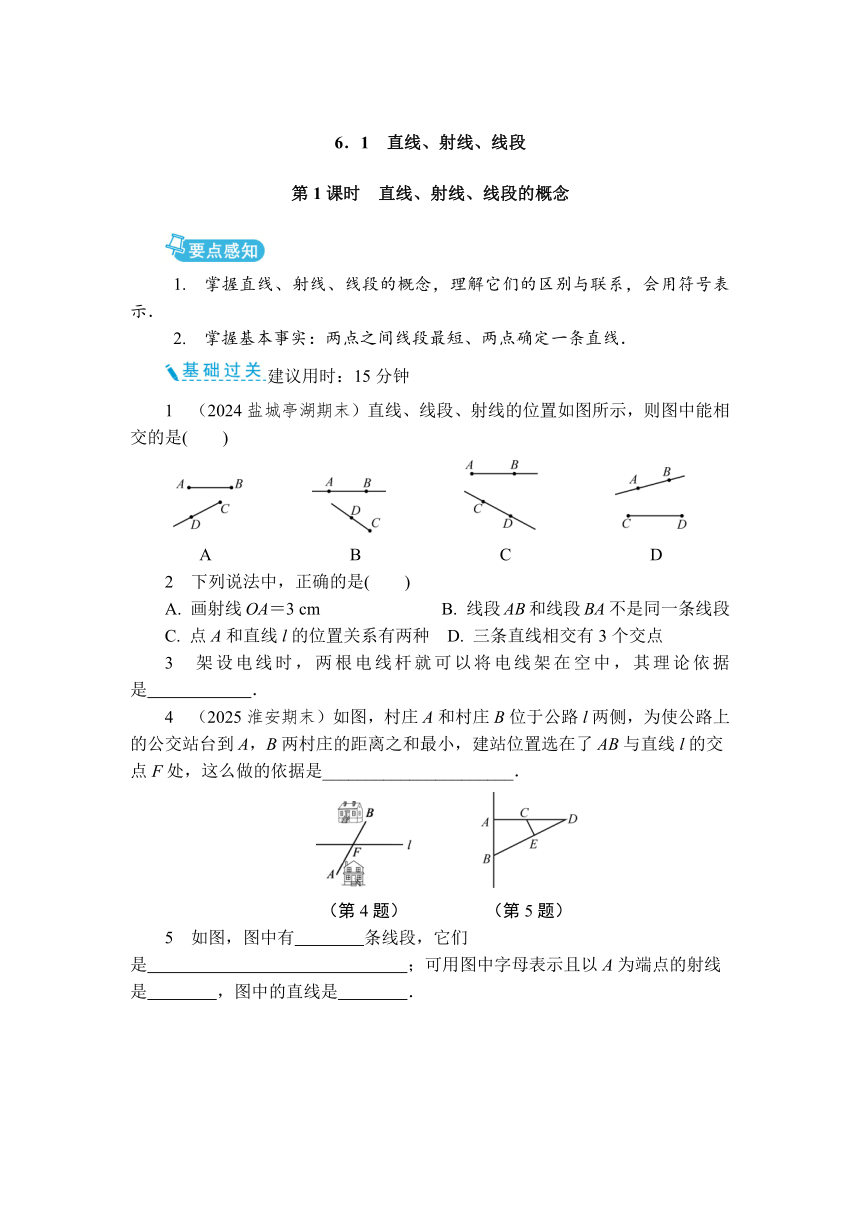 | |
| 格式 | docx | ||
| 文件大小 | 971.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 19:33:28 | ||
图片预览




文档简介
6.1 直线、射线、线段
第1课时 直线、射线、线段的概念
1. 掌握直线、射线、线段的概念,理解它们的区别与联系,会用符号表示.
2. 掌握基本事实:两点之间线段最短、两点确定一条直线.
建议用时:15分钟
1 (2024盐城亭湖期末)直线、线段、射线的位置如图所示,则图中能相交的是( )
A B C D
2 下列说法中,正确的是( )
A. 画射线OA=3 cm B. 线段AB和线段BA不是同一条线段
C. 点A和直线l的位置关系有两种 D. 三条直线相交有3个交点
3 架设电线时,两根电线杆就可以将电线架在空中,其理论依据是 .
4 (2025淮安期末)如图,村庄A和村庄B位于公路l两侧,为使公路上的公交站台到A,B两村庄的距离之和最小,建站位置选在了AB与直线l的交点F处,这么做的依据是______________________.
(第4题) (第5题)
5 如图,图中有 条线段,它们是 ;可用图中字母表示且以A为端点的射线是 ,图中的直线是 .
6 如图,平面上有四个点A,B,C,D,根据下列语句画图.
①画直线AB,CD交于点E;②画线段AC,BD交于点F;③连接EF交BC于点G;④连接AD,并将其反向延长;⑤作射线BC.
建议用时:20+5分钟
7 任意画三条不重合的直线,交点的个数是( )
A. 1 B. 1或3 C. 0或1或2或3 D. 不能确定
8 如果A站与B站之间还有3个车站,那么往返于A站与B站之间的车辆,应安排车票的种类数为( )
A. 4 B. 20 C. 10 D. 9
9 下列说法:①平面内两条不同的线段最多有一个公共点;②平面内两条不同的射线最多有一个公共点;③平面内两条不同的直线最多有一个公共点;④平面内一条直线和一条线段最多有一个公共点,其中正确的是 W.(填序号)
10 阅读下表:
线段AB上的点数n(包括A,B两点) 图例 线段总条数N
3 3=2+1
4 6=3+2+1
5 10=4+3+2+1
6 15=5+4+3+2+1
7
解答下列问题:
(1) 在表中空白处分别画出图形,写出线段总条数;
(2) 猜测线段总条数N与线段上的点数n(包括线段的两个端点)的关系是 ;
(3) 变式练习①:如果过每两点可以画一条直线,那么请在下面三组图中分别画直线,并回答问题:
图1最多可以画 条直线;图2最多可以画 条直线;图3最多可以画 条直线;
图1 图2 图3
归纳结论:如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画出直线 条(用含n的代数式表示);
变式练习②:某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物;
变式练习③:从A地到B地的火车途中共停靠7个站(不包括出发站和终点站),则共需准备 种车票.
第2课时 线段的长短
1. 学会比较线段的大小,学会画一条线段等于已知线段.
2. 理解线段的和、差,以及线段中点的意义,并会进行线段计算.
建议用时:15分钟
1 (2024南通启东期末)已知点M在线段AB上,则下列条件中不能判定M是线段AB中点的是( )
A. AM=BM B. AB=2AM C. BM=AB D. AM+BM=AB
2 如图,点B,C在线段AD上,且AB=CD,则AC与BD的大小关系是( )
A. AC>BD B. AC=BD C. AC<BD D. 不能确定
(第2题) (第3题) (第4题) (第5题)
3 如图,C是线段AB上一点,D是线段AC的中点,则下列等式中不一定成立的是( )
A. AD+BD=AB B. AC+BD-CD=AB
C. BD-BC=AD D. AB=2AC
4 如图,线段AB=3 cm,延长线段AB到点C,使BC=2AB,则AC=
cm.
5 如图,线段AB=18 cm,C是线段AB的中点,点D在线段CB上,DB=3 cm,则CD= cm.
6 (2025淮安淮阴期末)已知点A,B,C在同一直线上,AB=3 cm,BC=1 cm,则线段AC的长为 cm.
7 如图,C为线段AB上的一点,D为线段BC的中点,且BC=6 cm,AB=6CD.
(1) 图中共有 条线段;
(2) 求线段AC的长.
8 (2025南通通州期末)如图,已知线段a,b.
(1) 作线段AB=2a-b(要求:尺规作图,保留作图痕迹不写作法);
(2) 当a=2,b=3时,延长(1)中线段BA至点C,使AC=2AB,D是BC的中点,求BD的长.
建议用时:20+5分钟
9 (2024淮安金湖一模)如图,A,B,C,D是平面内的四点,若AC=4,BD=3, AD=BC=2, 则线段AB的长度可能是( )
A. 2 B. 4 C. 5 D. 6
(第9题) (第12题)
10 (2025南通如皋期末)已知互不重合的A,B,C三点在同一直线上,AB=2m,AC=2m+4,BC=4m+2,则这三点的位置关系是( )
A. 点A在B,C两点之间 B. 点C在A,B两点之间
C. 点B在A,C两点之间 D. 无法确定
11 (2025南京建邺期末)已知线段AB=5 cm,延长AB到点C,D是AC的中点,BD=1 cm,则线段AC的长是 cm.
12 (2024南通崇川月考)如图,C,D是线段AB上两点,已知图中所有线段的长度都是正整数,且总和为29,则线段AB的长度是 .
13 如图,已知C是线段AB上的一点,且AC∶BC=3∶2,D是线段AB的中点,且DC=6,求AD的长.
14 (2024泰州开学考试)如图,已知线段AB=12 cm,C为线段AB上的一个动点,D,E分别是AC和BC的中点.
若C恰好是AB的中点,则DE= cm;若AC=4 cm,则DE=
cm;
(2) 利用“字母代替数”的方法,证明不论AC取何值(不超过12 cm),DE的长不变.
6.1 直线、射线、线段
第1课时 直线、射线、线段的概念
1. B 2. C 3. 两点确定一条直线
4. 两点之间线段最短
5. 8 AD,AB,AC,BD,BE,CE,CD,DE AB AB
6. 如图所示.
7. C 8. B 9. ③
10. (1)
21=6+5+4+3+2+1
(2) N=
(3) ①3 6 10
画图如下:
图1 图2 图3
②1 225 2 450 ③36
第2课时 线段的长短
1. D 2. B 3. D 4. 9 5. 6 6. 2或4
7. (1) 6
(2) 因为D为线段BC的中点,BC=6 cm,
所以BD=CD=3 cm,
所以AB=6CD=6×3=18(cm),
所以AC=AB-BC=18-6=12(cm).
8. (1)
(2) 因为a=2,b=3,所以AB=2a-b=1.
因为AC=2AB,所以AC=2,所以BC=3.
因为D是BC的中点,所以BD=BC=1.5.
9. B 10. C 11. 8或12 12. 9或8
13. 设AC=3x,则BC=2x,AB=AC+BC=5x.
因为D为线段AB的中点,
所以AD=BD=AB=,
所以DC=BD-BC=-2x==6,
解得x=12,
所以AD=x=30.
14. (1) 6 6
(2) 因为D,E分别是AC,BC的中点,
所以CD=AC,CE=BC,
所以DE=CD+CE=AC+BC =(AC+BC) =AB.
因为AB=12 cm是固定值,所以DE的长不变.
第1课时 直线、射线、线段的概念
1. 掌握直线、射线、线段的概念,理解它们的区别与联系,会用符号表示.
2. 掌握基本事实:两点之间线段最短、两点确定一条直线.
建议用时:15分钟
1 (2024盐城亭湖期末)直线、线段、射线的位置如图所示,则图中能相交的是( )
A B C D
2 下列说法中,正确的是( )
A. 画射线OA=3 cm B. 线段AB和线段BA不是同一条线段
C. 点A和直线l的位置关系有两种 D. 三条直线相交有3个交点
3 架设电线时,两根电线杆就可以将电线架在空中,其理论依据是 .
4 (2025淮安期末)如图,村庄A和村庄B位于公路l两侧,为使公路上的公交站台到A,B两村庄的距离之和最小,建站位置选在了AB与直线l的交点F处,这么做的依据是______________________.
(第4题) (第5题)
5 如图,图中有 条线段,它们是 ;可用图中字母表示且以A为端点的射线是 ,图中的直线是 .
6 如图,平面上有四个点A,B,C,D,根据下列语句画图.
①画直线AB,CD交于点E;②画线段AC,BD交于点F;③连接EF交BC于点G;④连接AD,并将其反向延长;⑤作射线BC.
建议用时:20+5分钟
7 任意画三条不重合的直线,交点的个数是( )
A. 1 B. 1或3 C. 0或1或2或3 D. 不能确定
8 如果A站与B站之间还有3个车站,那么往返于A站与B站之间的车辆,应安排车票的种类数为( )
A. 4 B. 20 C. 10 D. 9
9 下列说法:①平面内两条不同的线段最多有一个公共点;②平面内两条不同的射线最多有一个公共点;③平面内两条不同的直线最多有一个公共点;④平面内一条直线和一条线段最多有一个公共点,其中正确的是 W.(填序号)
10 阅读下表:
线段AB上的点数n(包括A,B两点) 图例 线段总条数N
3 3=2+1
4 6=3+2+1
5 10=4+3+2+1
6 15=5+4+3+2+1
7
解答下列问题:
(1) 在表中空白处分别画出图形,写出线段总条数;
(2) 猜测线段总条数N与线段上的点数n(包括线段的两个端点)的关系是 ;
(3) 变式练习①:如果过每两点可以画一条直线,那么请在下面三组图中分别画直线,并回答问题:
图1最多可以画 条直线;图2最多可以画 条直线;图3最多可以画 条直线;
图1 图2 图3
归纳结论:如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画出直线 条(用含n的代数式表示);
变式练习②:某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物;
变式练习③:从A地到B地的火车途中共停靠7个站(不包括出发站和终点站),则共需准备 种车票.
第2课时 线段的长短
1. 学会比较线段的大小,学会画一条线段等于已知线段.
2. 理解线段的和、差,以及线段中点的意义,并会进行线段计算.
建议用时:15分钟
1 (2024南通启东期末)已知点M在线段AB上,则下列条件中不能判定M是线段AB中点的是( )
A. AM=BM B. AB=2AM C. BM=AB D. AM+BM=AB
2 如图,点B,C在线段AD上,且AB=CD,则AC与BD的大小关系是( )
A. AC>BD B. AC=BD C. AC<BD D. 不能确定
(第2题) (第3题) (第4题) (第5题)
3 如图,C是线段AB上一点,D是线段AC的中点,则下列等式中不一定成立的是( )
A. AD+BD=AB B. AC+BD-CD=AB
C. BD-BC=AD D. AB=2AC
4 如图,线段AB=3 cm,延长线段AB到点C,使BC=2AB,则AC=
cm.
5 如图,线段AB=18 cm,C是线段AB的中点,点D在线段CB上,DB=3 cm,则CD= cm.
6 (2025淮安淮阴期末)已知点A,B,C在同一直线上,AB=3 cm,BC=1 cm,则线段AC的长为 cm.
7 如图,C为线段AB上的一点,D为线段BC的中点,且BC=6 cm,AB=6CD.
(1) 图中共有 条线段;
(2) 求线段AC的长.
8 (2025南通通州期末)如图,已知线段a,b.
(1) 作线段AB=2a-b(要求:尺规作图,保留作图痕迹不写作法);
(2) 当a=2,b=3时,延长(1)中线段BA至点C,使AC=2AB,D是BC的中点,求BD的长.
建议用时:20+5分钟
9 (2024淮安金湖一模)如图,A,B,C,D是平面内的四点,若AC=4,BD=3, AD=BC=2, 则线段AB的长度可能是( )
A. 2 B. 4 C. 5 D. 6
(第9题) (第12题)
10 (2025南通如皋期末)已知互不重合的A,B,C三点在同一直线上,AB=2m,AC=2m+4,BC=4m+2,则这三点的位置关系是( )
A. 点A在B,C两点之间 B. 点C在A,B两点之间
C. 点B在A,C两点之间 D. 无法确定
11 (2025南京建邺期末)已知线段AB=5 cm,延长AB到点C,D是AC的中点,BD=1 cm,则线段AC的长是 cm.
12 (2024南通崇川月考)如图,C,D是线段AB上两点,已知图中所有线段的长度都是正整数,且总和为29,则线段AB的长度是 .
13 如图,已知C是线段AB上的一点,且AC∶BC=3∶2,D是线段AB的中点,且DC=6,求AD的长.
14 (2024泰州开学考试)如图,已知线段AB=12 cm,C为线段AB上的一个动点,D,E分别是AC和BC的中点.
若C恰好是AB的中点,则DE= cm;若AC=4 cm,则DE=
cm;
(2) 利用“字母代替数”的方法,证明不论AC取何值(不超过12 cm),DE的长不变.
6.1 直线、射线、线段
第1课时 直线、射线、线段的概念
1. B 2. C 3. 两点确定一条直线
4. 两点之间线段最短
5. 8 AD,AB,AC,BD,BE,CE,CD,DE AB AB
6. 如图所示.
7. C 8. B 9. ③
10. (1)
21=6+5+4+3+2+1
(2) N=
(3) ①3 6 10
画图如下:
图1 图2 图3
②1 225 2 450 ③36
第2课时 线段的长短
1. D 2. B 3. D 4. 9 5. 6 6. 2或4
7. (1) 6
(2) 因为D为线段BC的中点,BC=6 cm,
所以BD=CD=3 cm,
所以AB=6CD=6×3=18(cm),
所以AC=AB-BC=18-6=12(cm).
8. (1)
(2) 因为a=2,b=3,所以AB=2a-b=1.
因为AC=2AB,所以AC=2,所以BC=3.
因为D是BC的中点,所以BD=BC=1.5.
9. B 10. C 11. 8或12 12. 9或8
13. 设AC=3x,则BC=2x,AB=AC+BC=5x.
因为D为线段AB的中点,
所以AD=BD=AB=,
所以DC=BD-BC=-2x==6,
解得x=12,
所以AD=x=30.
14. (1) 6 6
(2) 因为D,E分别是AC,BC的中点,
所以CD=AC,CE=BC,
所以DE=CD+CE=AC+BC =(AC+BC) =AB.
因为AB=12 cm是固定值,所以DE的长不变.
同课章节目录
