6.2角 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 6.2角 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册 | 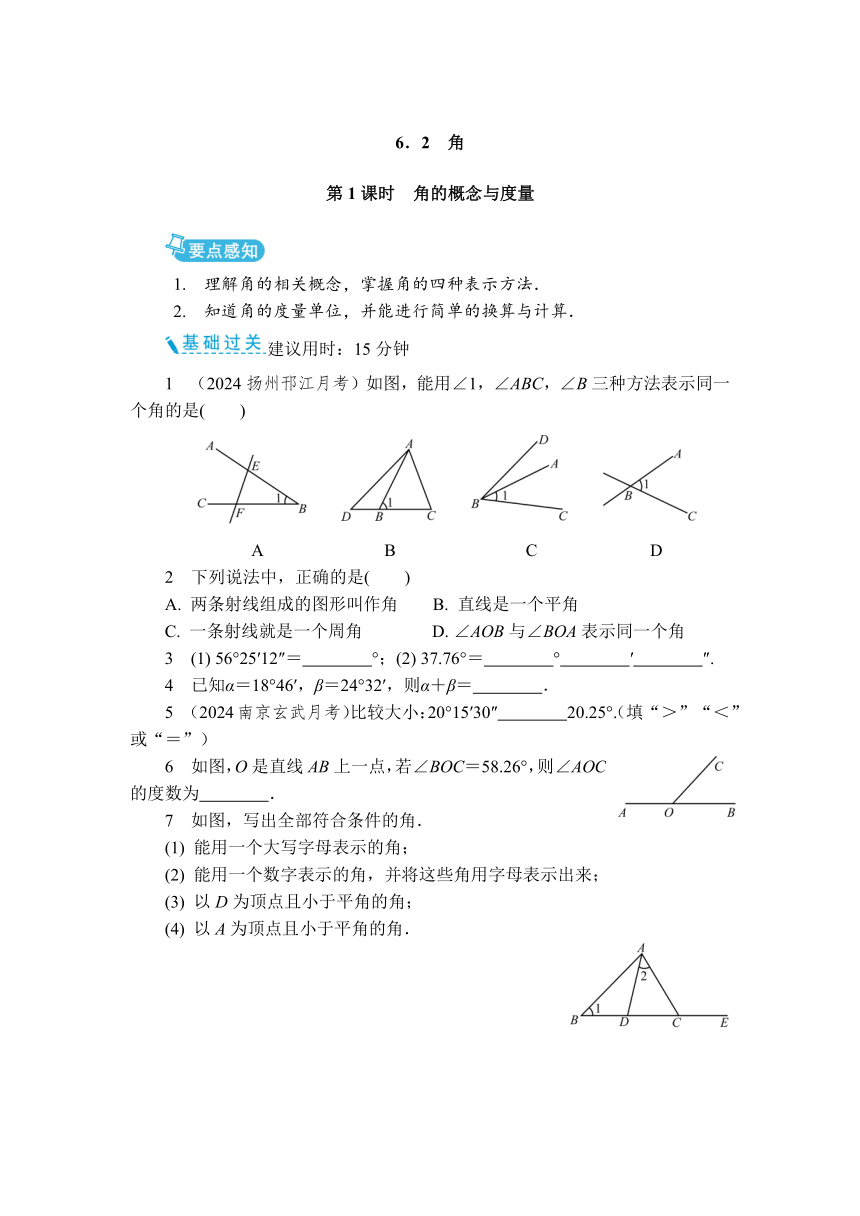 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 19:34:01 | ||
图片预览





文档简介
6.2 角
第1课时 角的概念与度量
1. 理解角的相关概念,掌握角的四种表示方法.
2. 知道角的度量单位,并能进行简单的换算与计算.
建议用时:15分钟
1 (2024扬州邗江月考)如图,能用∠1,∠ABC,∠B三种方法表示同一个角的是( )
A B C D
2 下列说法中,正确的是( )
A. 两条射线组成的图形叫作角 B. 直线是一个平角
C. 一条射线就是一个周角 D. ∠AOB与∠BOA表示同一个角
3 (1) 56°25′12″= °;(2) 37.76°= ° ′ ″.
4 已知α=18°46′,β=24°32′,则α+β= .
5 (2024南京玄武月考)比较大小:20°15′30″ 20.25°.(填“>”“<”或“=”)
6 如图,O是直线AB上一点,若∠BOC=58.26°,则∠AOC的度数为 .
7 如图,写出全部符合条件的角.
(1) 能用一个大写字母表示的角;
(2) 能用一个数字表示的角,并将这些角用字母表示出来;
(3) 以D为顶点且小于平角的角;
(4) 以A为顶点且小于平角的角.
8 计算:
(1) 49°38′+66°22′; (2) 180°-79°19′;
(3) 22°16′×5; (4) 182°36′÷4.
建议用时:20+5分钟
9 如图,直线m外有一定点O,A是直线m上的一个动点,当点A从右向左运动时,∠α和∠β的关系是( )
A. ∠α越来越小 B. ∠β越来越大
C. ∠α+∠β=180° D. ∠α和∠β均保持不变
(第9题) (第11题)
10 若∠AOB=45°,∠BOC=30°,则∠AOC等于( )
A. 75° B. 15° C. 75°或15° D. 不能确定
11 如图,若在∠AOE的内部从点O引出3条射线,则图中共有 个角;若引出5条射线,则有 个角;若引出n条射线,则有 个角.
12 如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC∶∠BOC=1∶2.
(1) 求∠AOC的度数;
(2) 过点O在∠AOB的内部作射线OD,若∠AOD=∠AOB,求∠COD的度数.
13 钟面角是指时钟的时针与分针所成的角.如图,在钟面上,点O为钟面的圆心,图中的圆我们称之为钟面圆.为便于研究,我们规定:钟面圆的半径OA表示时针,半径OB表示分针,它们所成的钟面角为∠AOB.本题中所提到的角都不小于0°,且不大于180°,所指的时刻都介于0点整到12点整之间.
(1) 时针每分钟转动的角度为 ,分针每分钟转动的角度为 ;
(2) 8点整,钟面角∠AOB= ,钟面角与此相等的整点还有 点;
(3) 在备用图中画出6点15分时半径OA,OB的大概位置,并求出此时∠AOB的度数.
备用图
第2课时 补角、余角
1. 理解补角、余角等概念,掌握同角(等角)的余角相等,同角(等角)的补角相等的性质.
2. 学会运用余角和补角的性质进行简单的推理计算.
建议用时:15分钟
1 (2024兰州)若∠A=80°,则∠A的补角是( )
A. 100° B. 80° C. 40° D. 10°
2 (2025盐城东台期末)小明同学用一副标准三角板想摆成∠α与∠β互余,下面摆放方式中符合要求的是( )
A B C D
3 已知∠1+∠2=180°,∠2+∠3=180°,则下列结论中正确的是( )
A. ∠1=∠3 B. ∠2=∠3
C. ∠1=∠2 D. ∠1=∠2=∠3
4 (2024泰州姜堰月考)已知∠1与∠2互余,∠2与∠3互补,且∠3=3∠1,则∠2的度数为( )
A. 30° B. 45° C. 60° D. 75°
5 (1) 若∠α=65°14′15″,则∠α的余角等于 ;
(2) 若∠A=59.6°,则它的余角为 ° ′.
6 已知∠1与∠2互余,∠1与∠3互补,则∠3-∠2= .
7 若一个角是另一个角的3倍,且小角的余角比大角的补角大20°,求这两个角的大小.
8 (2025苏州张家港期末)如图,已知∠α.
(1) 试画出∠α的一个余角(用∠1表示)和∠α的一个补角(用∠2表示);
(2) 若∠α=32°33′,则∠1= °,∠2= °.
建议用时:20+5分钟
9 (2025南通海安期末)若∠α和∠β互余,则下列式子中不能表示∠α补角的是( )
A. 180°-∠α B. ∠α+2∠β C. ∠β+90° D. 2∠α+∠β
10 如图,∠AOC=90°,点B,O,D在同一直线上.若∠1=26°,则∠2的大小为( )
A. 116° B. 84° C. 124° D. 106°
(第10题) (第11题)
11 (2025南京玄武期末)如图,点O在直线AB上,∠EOD=90°,∠COB=90°,则下列说法中错误的是( )
A. ∠1与∠2相等 B. ∠AOE与∠2互余
C. ∠AOE与∠COD互余 D. ∠AOC与∠COB互补
12 一个角的余角比这个角补角的大10°,则这个角的大小为 .
13 (2024泰州泰兴期中)将一副标准三角板的直角顶点O按如图所示位置叠放在一起.
(1) 填表:
∠BOD的大小 50° 60°
∠AOC的大小 150°
(2) 猜想∠BOD与∠AOC之间的数量关系,并说明理由.
14 以直线AB上的一点O为端点作射线OC,使∠BOC=40°,将一个直角三角板的直角顶点放在点O处,即∠DOE=90°.
(1) 如图1,若将直角三角板DOE的一边OE放在射线OA上,则∠COD= ;
(2) 如图2,将直角三角板DOE绕点O顺时针转动到某个位置,使得∠AOE=∠COE,则∠COD= ;
(3) 在直角三角板DOE绕点O顺时针转动(OD与OB重合时停止)的过程中,恰好有∠COD=∠AOE,求此时∠BOD的大小.
图1 图2
第3课时 角的大小比较
1. 通过度量、叠合等方法,会估计、比较角的大小.
2. 会用直尺和圆规作一个角等于已知角.
3. 理解并应用角平分线的概念解决问题.
建议用时:15分钟
1 如图,用三角板比较∠A与∠B的大小,其中正确的是( )
A. ∠A>∠B B. ∠A<∠B C. ∠A=∠B D. 不能确定
(第1题) (第2题) (第3题)
2 (2025无锡期末)如图,∠AOB是直角,∠AOC=50°, 射线OP从边OA出发,绕点O逆时针旋转直至与边OB重合,在旋转过程中,下列情形不可能出现的是( )
A. OP平分∠AOC B. OP平分∠AOB
C. OC平分∠BOP D. OC平分∠AOP
3 (2024泰州海陵期中)如图,∠DAE=100°,∠EAB=65°,根据图中尺规作图的痕迹,可知∠ABC的度数为 .
4 (2024连云港东海期末)已知小正方形网格如图所示,A,B,C,D,O均为格点,则∠AOB ∠COD.(填“>”“<”或“=”)
(第4题) (第5题)
5 (2024南京)如图,点A,O,B在同一条直线上,OD是∠AOC的平分线,OE是∠BOC的平分线.若∠AOE=162°,则∠BOD的度数为 W.
6 (2024南京期末)读句画图并求解:
(1) 如图,已知∠α.利用直尺和圆规画∠AOB,使∠AOB=∠α(保留作图痕迹,不写作法);
(2) 以∠AOB的顶点O为顶点,OB为一边画∠BOC,且∠BOC=60°;
(3) 若∠AOB=100°,求∠AOC的度数.
建议用时:20+5分钟
7 (2025南通启东期末)如图,已知∠AOB,以OA为边作∠AOC,使∠BOC=∠AOB,则下列结论中成立的是( )
A. ∠AOC=∠BOC
B. ∠AOC<∠AOB
C. ∠AOC=∠BOC或∠AOC=2∠BOC
D. ∠AOC=∠BOC或∠AOC=3∠BOC
(第7题) (第9题)
8 (2024徐州沛县月考)已知OC是∠AOB的平分线,∠BOD=∠COD,OE平分∠COD,设∠AOB=a,则∠BOE等于( )
A. a或a B. a或a C. a或a D. a
9 (2024南京玄武月考)如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°,那么∠2的度数是 W.
10 如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC∶∠BOC=1∶2.
(1) 求∠AOC和∠BOC的度数;
(2) 作射线OM平分∠AOC,在∠BOC内作射线ON,使得∠CON∶∠BON=1∶3,求∠MON的度数.
11 如图,将一副标准三角板摆放在一起,∠DAB=m°.
(1) 当0<m<45时,
①若m=20,则∠CAD= ,∠BAE= ;
②∠CAD与∠BAE的数量关系为 ;
(2) 当0<m<120,且∠BAE=6∠CAD时,求m的值.
6.2 角
第1课时 角的概念与度量
1. A 2. D 3. (1) 56.42 (2) 37 45 36
4. 43°18′ 5. > 6. 121.74°
7. (1) ∠B.
(2) ∠1可用∠ABD(∠ABC,∠ABE,∠B)表示,∠2可用∠CAD表示.
(3) ∠ADC,∠ADB.
(4) ∠BAD,∠DAC(∠2),∠BAC.
8. (1) 116° (2) 100°41′ (3) 111°20′ (4) 45°39′
9. C 10. C
11. 10 21 (n+1)(n+2)
12. (1) 因为∠AOC∶∠BOC=1∶2,∠AOB=120°,
所以∠AOC=∠AOB=×120°=40°.
(2) 因为∠AOD=∠AOB,
所以∠AOD=×120°=60°,
所以∠COD=∠AOD-∠AOC=60°-40°=20°.
13. (1) 0.5° 6°
(2) 120° 4
(3) 如图,∠AOB=6×30°+15×0.5°-15×6°=97.5°.
第2课时 补角、余角
1. A 2. A 3. A 4. B
5. (1) 24°45′45″ (2) 30 24
6. 90°
7. 设小角的大小为x°,则大角的大小为3x°.
由题意,得(90-x)-(180-3x)=20,
解得x=55,则3x=3×55=165.
故小角的大小为55°,大角的大小为165°.
8. (1) 如图.
(2) 57.45 147.45
9. D 10. A 11. C 12. 55°
13. (1) 30° 130° 120°
(2) ∠BOD+∠AOC=180°,理由如下:
设∠BOD=α,
则∠BOC=∠COD-∠BOD=90°-α,
所以∠AOC=∠BOC+∠AOB=90°-α+90°=180°-α,
所以∠BOD+∠AOC=180°.
14. (1) 50° (2) 20°
(3) ①如图1,当∠COD在∠BOC的内部时,
因为∠BOC=40°,
所以∠COD=40°-∠BOD.
因为∠AOE+∠EOD+∠BOD=180°,∠EOD=90°,
所以∠AOE=90°-∠BOD.
又因为∠COD=∠AOE,
所以40°-∠BOD=(90°-∠BOD),
解得∠BOD=15°;
②如图2,当∠COD在∠BOC的外部时,
因为∠BOC=40°,
所以∠COD=∠BOD-40°.
因为∠AOE+∠EOD+∠BOD=180°,∠EOD=90°,
所以∠AOE=90°-∠BOD.
又因为∠COD=∠AOE,
所以∠BOD-40°=(90°-∠BOD),
解得∠BOD=52.5°.
综上,∠BOD的大小为15°或52.5°.
图1 图2
第3课时 角的大小比较
1. B 2. D 3. 35° 4. > 5. 108°
6. (1) 如图所示,∠AOB即为所示.
(2) 如图所示,∠BOC和∠BOC′均为所求.
(3) 当射线OA和射线OC在射线OB同侧时,∠AOC=∠AOB-∠BOC=100°-60°=40°;
当射线OA和射线OC在射线OB异侧时,由图可知此时OC为OC′,则∠AOC′=∠AOB+∠BOC′=100°+60°=160°.
综上,∠AOC的度数为40°或160°.
7. D 8. A 9. 15°
10. (1) 设∠AOC=α,则∠BOC=2α,
因为∠AOB=120°,∠AOC+∠BOC=∠AOB,
所以α+2α=120°,
所以α=40°,所以∠AOC=40°,∠BOC=80°.
(2) 因为OM平分∠AOC,
所以∠MOC=∠COA=×40°=20°.
因为∠CON∶∠BON=1∶3,
所以∠NOC=∠COB=×80°=20°,
所以∠MON=∠COM+∠CON=20°+20°=40°.
11. (1) ① 25° 80° ②∠CAD+∠BAE=105°
(2) 当0<m≤45时,由∠BAE=6∠CAD,
得60+m=6(45-m),解得m=30;
当45<m<120时,由∠BAE=6∠CAD,
得m+60=6(m-45),解得m=66.
综上,m的值为30或66.
第1课时 角的概念与度量
1. 理解角的相关概念,掌握角的四种表示方法.
2. 知道角的度量单位,并能进行简单的换算与计算.
建议用时:15分钟
1 (2024扬州邗江月考)如图,能用∠1,∠ABC,∠B三种方法表示同一个角的是( )
A B C D
2 下列说法中,正确的是( )
A. 两条射线组成的图形叫作角 B. 直线是一个平角
C. 一条射线就是一个周角 D. ∠AOB与∠BOA表示同一个角
3 (1) 56°25′12″= °;(2) 37.76°= ° ′ ″.
4 已知α=18°46′,β=24°32′,则α+β= .
5 (2024南京玄武月考)比较大小:20°15′30″ 20.25°.(填“>”“<”或“=”)
6 如图,O是直线AB上一点,若∠BOC=58.26°,则∠AOC的度数为 .
7 如图,写出全部符合条件的角.
(1) 能用一个大写字母表示的角;
(2) 能用一个数字表示的角,并将这些角用字母表示出来;
(3) 以D为顶点且小于平角的角;
(4) 以A为顶点且小于平角的角.
8 计算:
(1) 49°38′+66°22′; (2) 180°-79°19′;
(3) 22°16′×5; (4) 182°36′÷4.
建议用时:20+5分钟
9 如图,直线m外有一定点O,A是直线m上的一个动点,当点A从右向左运动时,∠α和∠β的关系是( )
A. ∠α越来越小 B. ∠β越来越大
C. ∠α+∠β=180° D. ∠α和∠β均保持不变
(第9题) (第11题)
10 若∠AOB=45°,∠BOC=30°,则∠AOC等于( )
A. 75° B. 15° C. 75°或15° D. 不能确定
11 如图,若在∠AOE的内部从点O引出3条射线,则图中共有 个角;若引出5条射线,则有 个角;若引出n条射线,则有 个角.
12 如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC∶∠BOC=1∶2.
(1) 求∠AOC的度数;
(2) 过点O在∠AOB的内部作射线OD,若∠AOD=∠AOB,求∠COD的度数.
13 钟面角是指时钟的时针与分针所成的角.如图,在钟面上,点O为钟面的圆心,图中的圆我们称之为钟面圆.为便于研究,我们规定:钟面圆的半径OA表示时针,半径OB表示分针,它们所成的钟面角为∠AOB.本题中所提到的角都不小于0°,且不大于180°,所指的时刻都介于0点整到12点整之间.
(1) 时针每分钟转动的角度为 ,分针每分钟转动的角度为 ;
(2) 8点整,钟面角∠AOB= ,钟面角与此相等的整点还有 点;
(3) 在备用图中画出6点15分时半径OA,OB的大概位置,并求出此时∠AOB的度数.
备用图
第2课时 补角、余角
1. 理解补角、余角等概念,掌握同角(等角)的余角相等,同角(等角)的补角相等的性质.
2. 学会运用余角和补角的性质进行简单的推理计算.
建议用时:15分钟
1 (2024兰州)若∠A=80°,则∠A的补角是( )
A. 100° B. 80° C. 40° D. 10°
2 (2025盐城东台期末)小明同学用一副标准三角板想摆成∠α与∠β互余,下面摆放方式中符合要求的是( )
A B C D
3 已知∠1+∠2=180°,∠2+∠3=180°,则下列结论中正确的是( )
A. ∠1=∠3 B. ∠2=∠3
C. ∠1=∠2 D. ∠1=∠2=∠3
4 (2024泰州姜堰月考)已知∠1与∠2互余,∠2与∠3互补,且∠3=3∠1,则∠2的度数为( )
A. 30° B. 45° C. 60° D. 75°
5 (1) 若∠α=65°14′15″,则∠α的余角等于 ;
(2) 若∠A=59.6°,则它的余角为 ° ′.
6 已知∠1与∠2互余,∠1与∠3互补,则∠3-∠2= .
7 若一个角是另一个角的3倍,且小角的余角比大角的补角大20°,求这两个角的大小.
8 (2025苏州张家港期末)如图,已知∠α.
(1) 试画出∠α的一个余角(用∠1表示)和∠α的一个补角(用∠2表示);
(2) 若∠α=32°33′,则∠1= °,∠2= °.
建议用时:20+5分钟
9 (2025南通海安期末)若∠α和∠β互余,则下列式子中不能表示∠α补角的是( )
A. 180°-∠α B. ∠α+2∠β C. ∠β+90° D. 2∠α+∠β
10 如图,∠AOC=90°,点B,O,D在同一直线上.若∠1=26°,则∠2的大小为( )
A. 116° B. 84° C. 124° D. 106°
(第10题) (第11题)
11 (2025南京玄武期末)如图,点O在直线AB上,∠EOD=90°,∠COB=90°,则下列说法中错误的是( )
A. ∠1与∠2相等 B. ∠AOE与∠2互余
C. ∠AOE与∠COD互余 D. ∠AOC与∠COB互补
12 一个角的余角比这个角补角的大10°,则这个角的大小为 .
13 (2024泰州泰兴期中)将一副标准三角板的直角顶点O按如图所示位置叠放在一起.
(1) 填表:
∠BOD的大小 50° 60°
∠AOC的大小 150°
(2) 猜想∠BOD与∠AOC之间的数量关系,并说明理由.
14 以直线AB上的一点O为端点作射线OC,使∠BOC=40°,将一个直角三角板的直角顶点放在点O处,即∠DOE=90°.
(1) 如图1,若将直角三角板DOE的一边OE放在射线OA上,则∠COD= ;
(2) 如图2,将直角三角板DOE绕点O顺时针转动到某个位置,使得∠AOE=∠COE,则∠COD= ;
(3) 在直角三角板DOE绕点O顺时针转动(OD与OB重合时停止)的过程中,恰好有∠COD=∠AOE,求此时∠BOD的大小.
图1 图2
第3课时 角的大小比较
1. 通过度量、叠合等方法,会估计、比较角的大小.
2. 会用直尺和圆规作一个角等于已知角.
3. 理解并应用角平分线的概念解决问题.
建议用时:15分钟
1 如图,用三角板比较∠A与∠B的大小,其中正确的是( )
A. ∠A>∠B B. ∠A<∠B C. ∠A=∠B D. 不能确定
(第1题) (第2题) (第3题)
2 (2025无锡期末)如图,∠AOB是直角,∠AOC=50°, 射线OP从边OA出发,绕点O逆时针旋转直至与边OB重合,在旋转过程中,下列情形不可能出现的是( )
A. OP平分∠AOC B. OP平分∠AOB
C. OC平分∠BOP D. OC平分∠AOP
3 (2024泰州海陵期中)如图,∠DAE=100°,∠EAB=65°,根据图中尺规作图的痕迹,可知∠ABC的度数为 .
4 (2024连云港东海期末)已知小正方形网格如图所示,A,B,C,D,O均为格点,则∠AOB ∠COD.(填“>”“<”或“=”)
(第4题) (第5题)
5 (2024南京)如图,点A,O,B在同一条直线上,OD是∠AOC的平分线,OE是∠BOC的平分线.若∠AOE=162°,则∠BOD的度数为 W.
6 (2024南京期末)读句画图并求解:
(1) 如图,已知∠α.利用直尺和圆规画∠AOB,使∠AOB=∠α(保留作图痕迹,不写作法);
(2) 以∠AOB的顶点O为顶点,OB为一边画∠BOC,且∠BOC=60°;
(3) 若∠AOB=100°,求∠AOC的度数.
建议用时:20+5分钟
7 (2025南通启东期末)如图,已知∠AOB,以OA为边作∠AOC,使∠BOC=∠AOB,则下列结论中成立的是( )
A. ∠AOC=∠BOC
B. ∠AOC<∠AOB
C. ∠AOC=∠BOC或∠AOC=2∠BOC
D. ∠AOC=∠BOC或∠AOC=3∠BOC
(第7题) (第9题)
8 (2024徐州沛县月考)已知OC是∠AOB的平分线,∠BOD=∠COD,OE平分∠COD,设∠AOB=a,则∠BOE等于( )
A. a或a B. a或a C. a或a D. a
9 (2024南京玄武月考)如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°,那么∠2的度数是 W.
10 如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC∶∠BOC=1∶2.
(1) 求∠AOC和∠BOC的度数;
(2) 作射线OM平分∠AOC,在∠BOC内作射线ON,使得∠CON∶∠BON=1∶3,求∠MON的度数.
11 如图,将一副标准三角板摆放在一起,∠DAB=m°.
(1) 当0<m<45时,
①若m=20,则∠CAD= ,∠BAE= ;
②∠CAD与∠BAE的数量关系为 ;
(2) 当0<m<120,且∠BAE=6∠CAD时,求m的值.
6.2 角
第1课时 角的概念与度量
1. A 2. D 3. (1) 56.42 (2) 37 45 36
4. 43°18′ 5. > 6. 121.74°
7. (1) ∠B.
(2) ∠1可用∠ABD(∠ABC,∠ABE,∠B)表示,∠2可用∠CAD表示.
(3) ∠ADC,∠ADB.
(4) ∠BAD,∠DAC(∠2),∠BAC.
8. (1) 116° (2) 100°41′ (3) 111°20′ (4) 45°39′
9. C 10. C
11. 10 21 (n+1)(n+2)
12. (1) 因为∠AOC∶∠BOC=1∶2,∠AOB=120°,
所以∠AOC=∠AOB=×120°=40°.
(2) 因为∠AOD=∠AOB,
所以∠AOD=×120°=60°,
所以∠COD=∠AOD-∠AOC=60°-40°=20°.
13. (1) 0.5° 6°
(2) 120° 4
(3) 如图,∠AOB=6×30°+15×0.5°-15×6°=97.5°.
第2课时 补角、余角
1. A 2. A 3. A 4. B
5. (1) 24°45′45″ (2) 30 24
6. 90°
7. 设小角的大小为x°,则大角的大小为3x°.
由题意,得(90-x)-(180-3x)=20,
解得x=55,则3x=3×55=165.
故小角的大小为55°,大角的大小为165°.
8. (1) 如图.
(2) 57.45 147.45
9. D 10. A 11. C 12. 55°
13. (1) 30° 130° 120°
(2) ∠BOD+∠AOC=180°,理由如下:
设∠BOD=α,
则∠BOC=∠COD-∠BOD=90°-α,
所以∠AOC=∠BOC+∠AOB=90°-α+90°=180°-α,
所以∠BOD+∠AOC=180°.
14. (1) 50° (2) 20°
(3) ①如图1,当∠COD在∠BOC的内部时,
因为∠BOC=40°,
所以∠COD=40°-∠BOD.
因为∠AOE+∠EOD+∠BOD=180°,∠EOD=90°,
所以∠AOE=90°-∠BOD.
又因为∠COD=∠AOE,
所以40°-∠BOD=(90°-∠BOD),
解得∠BOD=15°;
②如图2,当∠COD在∠BOC的外部时,
因为∠BOC=40°,
所以∠COD=∠BOD-40°.
因为∠AOE+∠EOD+∠BOD=180°,∠EOD=90°,
所以∠AOE=90°-∠BOD.
又因为∠COD=∠AOE,
所以∠BOD-40°=(90°-∠BOD),
解得∠BOD=52.5°.
综上,∠BOD的大小为15°或52.5°.
图1 图2
第3课时 角的大小比较
1. B 2. D 3. 35° 4. > 5. 108°
6. (1) 如图所示,∠AOB即为所示.
(2) 如图所示,∠BOC和∠BOC′均为所求.
(3) 当射线OA和射线OC在射线OB同侧时,∠AOC=∠AOB-∠BOC=100°-60°=40°;
当射线OA和射线OC在射线OB异侧时,由图可知此时OC为OC′,则∠AOC′=∠AOB+∠BOC′=100°+60°=160°.
综上,∠AOC的度数为40°或160°.
7. D 8. A 9. 15°
10. (1) 设∠AOC=α,则∠BOC=2α,
因为∠AOB=120°,∠AOC+∠BOC=∠AOB,
所以α+2α=120°,
所以α=40°,所以∠AOC=40°,∠BOC=80°.
(2) 因为OM平分∠AOC,
所以∠MOC=∠COA=×40°=20°.
因为∠CON∶∠BON=1∶3,
所以∠NOC=∠COB=×80°=20°,
所以∠MON=∠COM+∠CON=20°+20°=40°.
11. (1) ① 25° 80° ②∠CAD+∠BAE=105°
(2) 当0<m≤45时,由∠BAE=6∠CAD,
得60+m=6(45-m),解得m=30;
当45<m<120时,由∠BAE=6∠CAD,
得m+60=6(m-45),解得m=66.
综上,m的值为30或66.
同课章节目录
