6.3 相交线 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 6.3 相交线 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 19:35:05 | ||
图片预览



文档简介
6.4 平 行 线
第1课时 平行线的概念
1. 会用平行线的概念判断两条直线平行,会过直线外一点画这条直线的平行线 .
2. 掌握平行线基本事实1:过直线外一点有且只有一条直线与这条直线平行.
建议用时:15分钟
1 关于同一平面内的两条线段,下列说法中正确的是( )
A. 一定平行 B. 一定相交
C. 可以既不平行又不相交 D. 不平行就相交
2 过直线l外一点A作l的平行线,可以作( )
A. 1条 B. 2条 C. 3条 D. 4条
3 (2025苏州高新区模拟)平面上两条直线的位置关系是 或 .
4 如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来: .
5 在同一平面内有两条不同的直线a,b,分别根据下列情形,写出a,b的位置关系.
(1) 如果它们没有公共点,那么 ;
(2) 如果它们都平行于第三条直线,那么 ;
(3) 如果它们有且只有一个公共点,那么 .
6 如图,已知直线a,点B,C.
(1) 过点B画直线a的平行线,能画几条?
(2) 过点C画直线a的平行线,它与过点B的平行线平行吗?
7 如图,在∠AOB内有一点P.
(1) 过点P画l1∥OA;
(2) 过点P画l2∥OB;
(3) l1,l2的夹角与∠O的大小有怎样的关系?
建议用时:20+5分钟
8 已知∠AOB,P是任意一点,过点P画一条直线与OA平行,则这样的直线( )
A. 有且仅有一条 B. 有两条
C. 不存在 D. 有一条或不存在
9 同一平面内的四条直线无论其位置关系如何,它们的交点个数不可能是( )
A. 0 B. 2 C. 3 D. 5
10 同一平面内有三条直线,如果只有两条平行,那么它们的交点个数为( )
A. 0 B. 1 C. 2 D. 3
11 给出下列说法:①不相交的两条直线是平行线;②过一点有且只有一条直线和已知直线平行;③过两条直线a,b外的一点P,画直线c,使c∥a,且c∥b;④在同一平面内,不相交的两条直线一定平行.其中正确的个数为( )
A. 4 B. 3 C. 2 D. 1
12 平面内四条直线共有三个交点,则这四条直线中最多有 条平行线.
13 如图,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字母“M”.
(1) 请从正面、上面、右面三个不同方向上各找出一组平行线段,并用字母表示出来;
(2) EF与A′B′有何位置关系?
14 (2024苏州期末)如图,方格纸中每个小正方形的边长都是1.
(1) 过点P分别画PM∥AC,PN∥AB,PM与AB相交于点M,PN与AC相交于点N;
(2) 求四边形PMAN的面积.
15 平面内的1条直线可以将平面分成2个部分,2条直线最多可以将平面分成4个部分,3条直线最多可以将平面分成7个部分……总结规律,10条直线最多可以将平面分成几个部分?
第2课时 平行线的判定——同位角
1. 会正确识别同位角.
2. 会用同位角相等判定两直线平行.
建议用时:15分钟
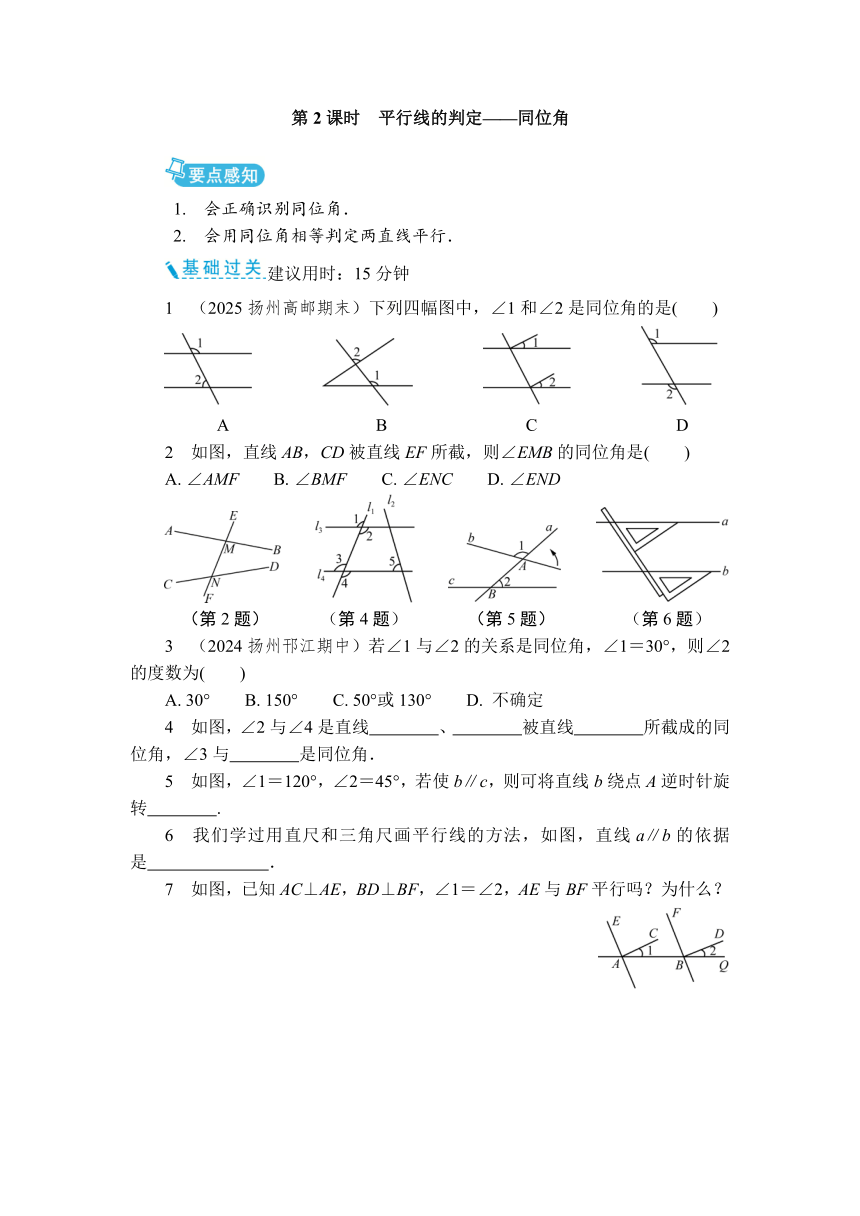
1 (2025扬州高邮期末)下列四幅图中,∠1和∠2是同位角的是( )
A B C D
2 如图,直线AB,CD被直线EF所截,则∠EMB的同位角是( )
A. ∠AMF B. ∠BMF C. ∠ENC D. ∠END
(第2题) (第4题) (第5题) (第6题)
3 (2024扬州邗江期中)若∠1与∠2的关系是同位角,∠1=30°,则∠2的度数为( )
A. 30° B. 150° C. 50°或130° D. 不确定
4 如图,∠2与∠4是直线 、 被直线 所截成的同位角,∠3与 是同位角.
5 如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转 .
6 我们学过用直尺和三角尺画平行线的方法,如图,直线a∥b的依据是 .
7 如图,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
建议用时:20+5分钟
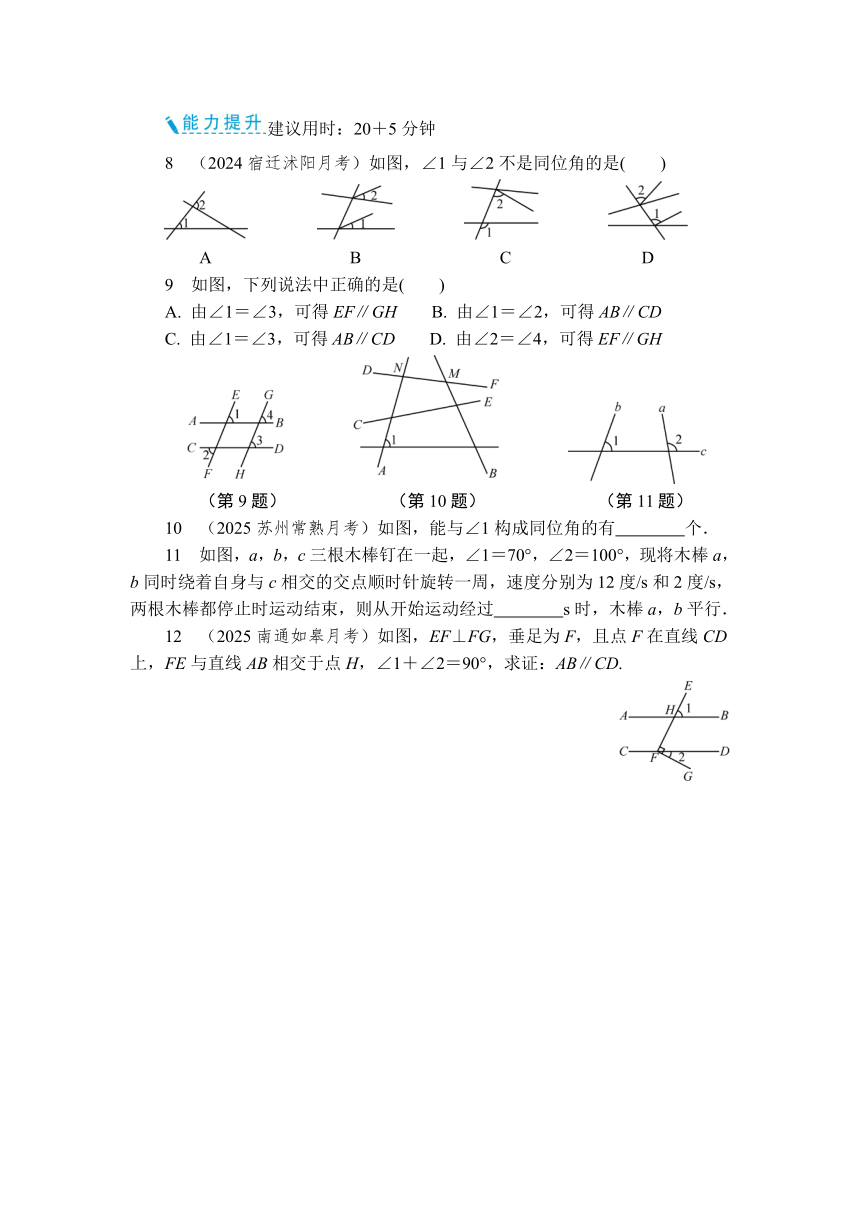
8 (2024宿迁沭阳月考)如图,∠1与∠2不是同位角的是( )
A B C D
9 如图,下列说法中正确的是( )
A. 由∠1=∠3,可得EF∥GH B. 由∠1=∠2,可得AB∥CD
C. 由∠1=∠3,可得AB∥CD D. 由∠2=∠4,可得EF∥GH
(第9题) (第10题) (第11题)
10 (2025苏州常熟月考)如图,能与∠1构成同位角的有 个.
11 如图,a,b,c三根木棒钉在一起,∠1=70°,∠2=100°,现将木棒a,b同时绕着自身与c相交的交点顺时针旋转一周,速度分别为12度/s和2度/s,两根木棒都停止时运动结束,则从开始运动经过 s时,木棒a,b平行.
12 (2025南通如皋月考)如图,EF⊥FG,垂足为F,且点F在直线CD上,FE与直线AB相交于点H,∠1+∠2=90°,求证:AB∥CD.
13 我们知道“在同一平面内,经过直线外一点有且只有一条直线与已知直线平行”.
小伟同学想通过“同位角相等,两直线平行”作出图形,具体作法是:过点P任意作一条直线a与直线l相交,再以P为顶点作一个角,直线a为角的一边所在直线,则角的另一边所在直线与直线l平行.
(1) 请你参照小伟同学的作法,帮他完成剩余的作图(保留作图痕迹,不写作法);
(2) 你还有其他办法吗?请在备用图中完成(只需一种即可,保留作图痕迹,不写作法).
备用图
第3课时 平行线的判定——内错角、同旁内角
1. 会正确识别内错角,同旁内角.
2. 能用内错角相等(或同旁内角互补),判定两直线平行.
建议用时:15分钟
1 (2024宿迁宿豫期中)如图,下列结论中错误的是( )
A. ∠1与∠2是同旁内角 B. ∠1与∠6是内错角
C. ∠2与∠5是内错角 D. ∠3与∠5是同位角
(第1题) (第2题) (第3题) (第4题) (第5题)
2 (2025泰州姜堰期末)如图,下列条件中不能判定AB∥CD的是( )
A. ∠3+∠5=180° B. ∠1=∠5 C. ∠3=∠4 D. ∠1=∠2
3 如图,(1) ∠1与∠2是直线 、 被直线 所截的 角;
(2) ∠3与 是内错角;
(3) ∠2与 是直线 、 被直线 所截的同旁内角;
(4) ∠1与∠3是直线 、 被直线 所截的 角.
4 如图,若添加一个条件可使DE∥AC,则任意写一个符合要求的条件: W.
5 如图,(1) 从∠1=∠4,可以推出 ∥ ,理由是
;
(2) 从∠ABC+∠ =180°,可以推出AB∥CD,理由是
;
(3) 从∠3=∠ ,可以推出AD∥BC,理由是 ;
(4) 从∠5=∠ ,可以推出AB∥CD,理由是 .
6 如图,CE平分∠ACD,∠1=∠2.判断AB与CD是否平行,并说明理由.
解:AB∥CD,理由如下:
因为CE平分∠ACD,
所以∠ =∠ ( ).
因为∠1=∠2(已知),
所以∠1=∠ ( ),
所以AB∥CD( ).
建议用时:20+5分钟
7 (2024徐州邳州期中)如图,直线AD,BE被直线BF和AC所截,则下列说法中正确的是( )
A. ∠3与∠4是同旁内角 B. ∠2与∠5是同位角
C. ∠6与∠1是内错角 D. ∠2与∠6是同旁内角
(第7题) (第8题) (第9题) (第10题)
8 (2025南通海门月考)如图,下列条件中不能判定CF∥BE的是( )
A. ∠1=∠B B. ∠1=∠C
C. ∠CFB+∠B=180° D. ∠CFP=∠FPB
9 将一副标准三角板按如图方式(共顶点A)叠放在一起,若固定三角板ABC,改变三角板ADE的位置(其中点A位置始终不变),当∠BAD= 时,DE∥AB.
10 (2024常州天宁期中)如图,直线EF上有两点A,C,分别引两条射线AB,CD,∠DCF=60°,∠EAB=70°,射线AB,CD分别绕点A,C以1度/s和4度/s的速度同时顺时针转动,在射线CD转动一周的时间内,使得CD∥AB的所有满足条件的时间为 s.
11 (2024无锡锡山月考)如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,求证:EC∥DF.
12 已知直线AB和CD被直线MN所截.
(1) 如图1,若EG平分∠BEF,FH平分∠DFE,则∠1与∠2满足什么条件时,AB∥CD?为什么?
(2) 如图2,若EG平分∠MEB,FH平分∠DFE,则∠1与∠2满足什么条件时,AB∥CD?为什么?
(3) 如图3,若EG平分∠AEF,FH平分∠DFE,则∠1与∠2满足什么条件时,AB∥CD?为什么?
图1 图2 图3
第4课时 平行线的性质
1. 掌握平行线的三条性质定理.
2. 综合运用平行线的性质和判定定理解决问题.
建议用时:15分钟
1 (2024重庆)如图,AB∥CD,∠1=65°,则∠2的度数是( )
A. 105° B. 115° C. 125° D. 135°
(第1题) (第2题) (第3题) (第4题)
2 (2024盐城)小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为( )
A. 25° B. 35° C. 45° D. 55°
3 (2024资阳)如图,AB∥CD,过点D作DE⊥AC于点E. 若∠D=50°,则∠A的度数为( )
A. 130° B. 140° C. 150° D. 160°
4 (2024陕西)如图,AB∥DC,BC∥DE,∠B=145°,则∠D的度数为( )
A. 25° B. 35° C. 45° D. 55°
5 将一副标准三角板按如图方式放置,其中AB∥DE,则∠CDF= .
(第5题) (第6题)
6 (2024常州天宁期中)如图,将一个宽度相等的纸条按如图所示沿AB折叠,已知∠1=50°,则∠2= .
7 如图,AE∥BD,∠EAB=130°,∠EFD=30°,求∠C的度数.
建议用时:20+5分钟
8 (2024南充)如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40°,则∠3的度数为( )
A. 80° B. 90° C. 100° D. 120°
图1 图2
(第8题) (第10题) (第11题)
9 (2025南通海门月考)若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x-20)°,则∠α的度数为( )
A. 70° B. 30° C. 70°或86° D. 30°或38°
10 (2025南通启东月考)如图,直尺的一边经过直角三角板60°的顶点,另一边与三角板的两条直角边分别相交,若∠1=32°,则∠2= .
11 (2025南通启东月考)图1是一打孔器的实物图,图2是使用打孔器的侧面示意图,AD∥BC,使用打孔器时,AD,DE,DC分别移动到AD′,D′E′,D′C,此时D′E′∥BC,DD′平分∠ADC,若∠DD′E′=62°,则∠DCB= .
12 (2024苏州吴江期中)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
13 (2025南通如皋月考)如图,AC∥FE,∠1+∠2=180°.
(1) 求证:∠FAB=∠BDC;
(2) 若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
6.4 平 行 线
第1课时 平行线的概念
1. C 2. A 3. 相交 平行 4. CD∥MN,GH∥PN
5. (1) a∥b (2) a∥b (3) a与b相交
6. (1) 一条
(2) 平行
7. (1) 略 (2) 略
(3) l1,l2的夹角与∠O相等或互补.
8. D 9. B 10. C 11. D 12. 3
13. (1) (答案不唯一)正面:AB∥EF;上面:A′B′∥AB;右面:DD′∥HR
(2) EF∥A′B′
14. (1) 如图,点M,点N即为所求.
(2) 四边形PMAN的面积为5×7-×3×3-×2×4-×3×3-×2×4=18.
15. 由图可知,
有一条直线时,最多分成2部分;
有两条直线时,最多分成2+2=4部分;
有三条直线时,最多分成1+1+2+3=7部分;
设有n条直线,分成的平面最多有m个,则
m=1+1+…+(n-1)+n=n(n+1)+1,
当n=10时,×10×11+1=56,
故10条直线最多可以将平面分成56个部分.
第2课时 平行线的判定——同位角
1. B 2. D 3. D 4. l3 l4 l1 ∠1,∠5
5. 15° 6. 同位角相等,两直线平行
7. 平行,理由如下:
因为AC⊥AE,BD⊥BF,∠1=∠2,
所以∠EAB=∠FBQ,
所以AE∥BF(同位角相等,两直线平行).
8. B 9. B 10. 3 11. 3或21或75或165
12. 因为EF⊥FG,
所以∠EFG=90°,
即∠EFD+∠2=90°.
又因为∠1+∠2=90°,
所以∠EFD=∠1,
所以AB∥CD.
13. (1) 如图,直线m即为所求.
(2) 如图,直线m即为所求.
第3课时 平行线的判定——内错角、同旁内角
1. C 2. D
3. (1) DE BC AB 同位 (2) ∠4 (3) ∠BFA AB AF BC或∠BED ED BC AB (4) AB AF DE 内错
4. ∠1=∠A(答案不唯一)
5. (1) AB CD 内错角相等,两直线平行
(2) BCD 同旁内角互补,两直线平行
(3) 2 内错角相等,两直线平行
(4) ABC 同位角相等,两直线平行
6. 2 ECD 角平分线的定义
ECD 等量代换
内错角相等,两直线平行
7. D 8. B 9. 30°或150° 10. 或
11. 因为BD平分∠ABC,
所以∠DBF=∠ABC.
因为CE平分∠ACB,
所以∠ECB=∠ACB.
因为∠ABC=∠ACB,
所以∠DBF=∠ECB.
因为∠DBF=∠F,
所以∠ECB=∠F,
所以EC∥DF.
12. (1) 当∠1+∠2=90°时,AB∥CD,理由如下:
因为EG平分∠BEF,FH平分∠DFE,
所以∠BEF=2∠1,∠DFE=2∠2.
因为∠1+∠2=90°,
所以∠BEF+∠DFE=180°,
所以AB∥CD.
(2) 当∠1=∠2时,AB∥CD,理由如下:
因为EG平分∠BEM,FH平分∠DFE,
所以∠BEM=2∠1,∠DFE=2∠2.
因为∠1=∠2,
所以∠BEM=∠DFE,
所以AB∥CD.
(3) 当∠1=∠2时,AB∥CD,理由如下:
因为EG平分∠AEF,FH平分∠DFE,
所以∠AEF=2∠1,∠DFE=2∠2.
因为∠1=∠2,
所以∠AEF=∠DFE,
所以AB∥CD.
第4课时 平行线的性质
1. B 2. B 3. B 4. B 5. 105° 6. 100°
7. 因为AE∥BD,∠EAB=130°,∠EFD=30°,
所以∠CBD=130°,∠CFB=30°,
所以∠C=180°-∠CBD-∠CFB=180°-130°-30°=20°.
8. C 9. C 10. 152° 11. 56°
12. 因为EF∥AD,
所以∠2=∠3.
因为∠1=∠2,
所以∠1=∠3,
所以DG∥AB,
所以∠BAC+∠AGD=180°.
因为∠BAC=70°,所以∠AGD=110°.
13. (1) 因为AC∥EF,
所以∠1+∠FAC=180°.
因为∠1+∠2=180°,
所以∠FAC=∠2,
所以FA∥CD,
所以∠FAB=∠BDC.
(2) 因为AC平分∠FAD,
所以∠FAC=∠CAD,∠FAD=2∠FAC.
由(1)知∠FAC=∠2,
所以∠FAD=2∠2,
所以∠2=∠FAD.
因为∠FAD=80°,
所以∠2=×80°=40°.
因为EF⊥BE,AC∥EF,
所以AC⊥BE,
所以∠ACB=90°,
所以∠BCD=90°-∠2=50°.
第1课时 平行线的概念
1. 会用平行线的概念判断两条直线平行,会过直线外一点画这条直线的平行线 .
2. 掌握平行线基本事实1:过直线外一点有且只有一条直线与这条直线平行.
建议用时:15分钟
1 关于同一平面内的两条线段,下列说法中正确的是( )
A. 一定平行 B. 一定相交
C. 可以既不平行又不相交 D. 不平行就相交
2 过直线l外一点A作l的平行线,可以作( )
A. 1条 B. 2条 C. 3条 D. 4条
3 (2025苏州高新区模拟)平面上两条直线的位置关系是 或 .
4 如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来: .
5 在同一平面内有两条不同的直线a,b,分别根据下列情形,写出a,b的位置关系.
(1) 如果它们没有公共点,那么 ;
(2) 如果它们都平行于第三条直线,那么 ;
(3) 如果它们有且只有一个公共点,那么 .
6 如图,已知直线a,点B,C.
(1) 过点B画直线a的平行线,能画几条?
(2) 过点C画直线a的平行线,它与过点B的平行线平行吗?
7 如图,在∠AOB内有一点P.
(1) 过点P画l1∥OA;
(2) 过点P画l2∥OB;
(3) l1,l2的夹角与∠O的大小有怎样的关系?
建议用时:20+5分钟
8 已知∠AOB,P是任意一点,过点P画一条直线与OA平行,则这样的直线( )
A. 有且仅有一条 B. 有两条
C. 不存在 D. 有一条或不存在
9 同一平面内的四条直线无论其位置关系如何,它们的交点个数不可能是( )
A. 0 B. 2 C. 3 D. 5
10 同一平面内有三条直线,如果只有两条平行,那么它们的交点个数为( )
A. 0 B. 1 C. 2 D. 3
11 给出下列说法:①不相交的两条直线是平行线;②过一点有且只有一条直线和已知直线平行;③过两条直线a,b外的一点P,画直线c,使c∥a,且c∥b;④在同一平面内,不相交的两条直线一定平行.其中正确的个数为( )
A. 4 B. 3 C. 2 D. 1
12 平面内四条直线共有三个交点,则这四条直线中最多有 条平行线.
13 如图,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字母“M”.
(1) 请从正面、上面、右面三个不同方向上各找出一组平行线段,并用字母表示出来;
(2) EF与A′B′有何位置关系?
14 (2024苏州期末)如图,方格纸中每个小正方形的边长都是1.
(1) 过点P分别画PM∥AC,PN∥AB,PM与AB相交于点M,PN与AC相交于点N;
(2) 求四边形PMAN的面积.
15 平面内的1条直线可以将平面分成2个部分,2条直线最多可以将平面分成4个部分,3条直线最多可以将平面分成7个部分……总结规律,10条直线最多可以将平面分成几个部分?
第2课时 平行线的判定——同位角
1. 会正确识别同位角.
2. 会用同位角相等判定两直线平行.
建议用时:15分钟
1 (2025扬州高邮期末)下列四幅图中,∠1和∠2是同位角的是( )
A B C D
2 如图,直线AB,CD被直线EF所截,则∠EMB的同位角是( )
A. ∠AMF B. ∠BMF C. ∠ENC D. ∠END
(第2题) (第4题) (第5题) (第6题)
3 (2024扬州邗江期中)若∠1与∠2的关系是同位角,∠1=30°,则∠2的度数为( )
A. 30° B. 150° C. 50°或130° D. 不确定
4 如图,∠2与∠4是直线 、 被直线 所截成的同位角,∠3与 是同位角.
5 如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转 .
6 我们学过用直尺和三角尺画平行线的方法,如图,直线a∥b的依据是 .
7 如图,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
建议用时:20+5分钟
8 (2024宿迁沭阳月考)如图,∠1与∠2不是同位角的是( )
A B C D
9 如图,下列说法中正确的是( )
A. 由∠1=∠3,可得EF∥GH B. 由∠1=∠2,可得AB∥CD
C. 由∠1=∠3,可得AB∥CD D. 由∠2=∠4,可得EF∥GH
(第9题) (第10题) (第11题)
10 (2025苏州常熟月考)如图,能与∠1构成同位角的有 个.
11 如图,a,b,c三根木棒钉在一起,∠1=70°,∠2=100°,现将木棒a,b同时绕着自身与c相交的交点顺时针旋转一周,速度分别为12度/s和2度/s,两根木棒都停止时运动结束,则从开始运动经过 s时,木棒a,b平行.
12 (2025南通如皋月考)如图,EF⊥FG,垂足为F,且点F在直线CD上,FE与直线AB相交于点H,∠1+∠2=90°,求证:AB∥CD.
13 我们知道“在同一平面内,经过直线外一点有且只有一条直线与已知直线平行”.
小伟同学想通过“同位角相等,两直线平行”作出图形,具体作法是:过点P任意作一条直线a与直线l相交,再以P为顶点作一个角,直线a为角的一边所在直线,则角的另一边所在直线与直线l平行.
(1) 请你参照小伟同学的作法,帮他完成剩余的作图(保留作图痕迹,不写作法);
(2) 你还有其他办法吗?请在备用图中完成(只需一种即可,保留作图痕迹,不写作法).
备用图
第3课时 平行线的判定——内错角、同旁内角
1. 会正确识别内错角,同旁内角.
2. 能用内错角相等(或同旁内角互补),判定两直线平行.
建议用时:15分钟
1 (2024宿迁宿豫期中)如图,下列结论中错误的是( )
A. ∠1与∠2是同旁内角 B. ∠1与∠6是内错角
C. ∠2与∠5是内错角 D. ∠3与∠5是同位角
(第1题) (第2题) (第3题) (第4题) (第5题)
2 (2025泰州姜堰期末)如图,下列条件中不能判定AB∥CD的是( )
A. ∠3+∠5=180° B. ∠1=∠5 C. ∠3=∠4 D. ∠1=∠2
3 如图,(1) ∠1与∠2是直线 、 被直线 所截的 角;
(2) ∠3与 是内错角;
(3) ∠2与 是直线 、 被直线 所截的同旁内角;
(4) ∠1与∠3是直线 、 被直线 所截的 角.
4 如图,若添加一个条件可使DE∥AC,则任意写一个符合要求的条件: W.
5 如图,(1) 从∠1=∠4,可以推出 ∥ ,理由是
;
(2) 从∠ABC+∠ =180°,可以推出AB∥CD,理由是
;
(3) 从∠3=∠ ,可以推出AD∥BC,理由是 ;
(4) 从∠5=∠ ,可以推出AB∥CD,理由是 .
6 如图,CE平分∠ACD,∠1=∠2.判断AB与CD是否平行,并说明理由.
解:AB∥CD,理由如下:
因为CE平分∠ACD,
所以∠ =∠ ( ).
因为∠1=∠2(已知),
所以∠1=∠ ( ),
所以AB∥CD( ).
建议用时:20+5分钟
7 (2024徐州邳州期中)如图,直线AD,BE被直线BF和AC所截,则下列说法中正确的是( )
A. ∠3与∠4是同旁内角 B. ∠2与∠5是同位角
C. ∠6与∠1是内错角 D. ∠2与∠6是同旁内角
(第7题) (第8题) (第9题) (第10题)
8 (2025南通海门月考)如图,下列条件中不能判定CF∥BE的是( )
A. ∠1=∠B B. ∠1=∠C
C. ∠CFB+∠B=180° D. ∠CFP=∠FPB
9 将一副标准三角板按如图方式(共顶点A)叠放在一起,若固定三角板ABC,改变三角板ADE的位置(其中点A位置始终不变),当∠BAD= 时,DE∥AB.
10 (2024常州天宁期中)如图,直线EF上有两点A,C,分别引两条射线AB,CD,∠DCF=60°,∠EAB=70°,射线AB,CD分别绕点A,C以1度/s和4度/s的速度同时顺时针转动,在射线CD转动一周的时间内,使得CD∥AB的所有满足条件的时间为 s.
11 (2024无锡锡山月考)如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,求证:EC∥DF.
12 已知直线AB和CD被直线MN所截.
(1) 如图1,若EG平分∠BEF,FH平分∠DFE,则∠1与∠2满足什么条件时,AB∥CD?为什么?
(2) 如图2,若EG平分∠MEB,FH平分∠DFE,则∠1与∠2满足什么条件时,AB∥CD?为什么?
(3) 如图3,若EG平分∠AEF,FH平分∠DFE,则∠1与∠2满足什么条件时,AB∥CD?为什么?
图1 图2 图3
第4课时 平行线的性质
1. 掌握平行线的三条性质定理.
2. 综合运用平行线的性质和判定定理解决问题.
建议用时:15分钟
1 (2024重庆)如图,AB∥CD,∠1=65°,则∠2的度数是( )
A. 105° B. 115° C. 125° D. 135°
(第1题) (第2题) (第3题) (第4题)
2 (2024盐城)小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为( )
A. 25° B. 35° C. 45° D. 55°
3 (2024资阳)如图,AB∥CD,过点D作DE⊥AC于点E. 若∠D=50°,则∠A的度数为( )
A. 130° B. 140° C. 150° D. 160°
4 (2024陕西)如图,AB∥DC,BC∥DE,∠B=145°,则∠D的度数为( )
A. 25° B. 35° C. 45° D. 55°
5 将一副标准三角板按如图方式放置,其中AB∥DE,则∠CDF= .
(第5题) (第6题)
6 (2024常州天宁期中)如图,将一个宽度相等的纸条按如图所示沿AB折叠,已知∠1=50°,则∠2= .
7 如图,AE∥BD,∠EAB=130°,∠EFD=30°,求∠C的度数.
建议用时:20+5分钟
8 (2024南充)如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40°,则∠3的度数为( )
A. 80° B. 90° C. 100° D. 120°
图1 图2
(第8题) (第10题) (第11题)
9 (2025南通海门月考)若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x-20)°,则∠α的度数为( )
A. 70° B. 30° C. 70°或86° D. 30°或38°
10 (2025南通启东月考)如图,直尺的一边经过直角三角板60°的顶点,另一边与三角板的两条直角边分别相交,若∠1=32°,则∠2= .
11 (2025南通启东月考)图1是一打孔器的实物图,图2是使用打孔器的侧面示意图,AD∥BC,使用打孔器时,AD,DE,DC分别移动到AD′,D′E′,D′C,此时D′E′∥BC,DD′平分∠ADC,若∠DD′E′=62°,则∠DCB= .
12 (2024苏州吴江期中)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
13 (2025南通如皋月考)如图,AC∥FE,∠1+∠2=180°.
(1) 求证:∠FAB=∠BDC;
(2) 若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
6.4 平 行 线
第1课时 平行线的概念
1. C 2. A 3. 相交 平行 4. CD∥MN,GH∥PN
5. (1) a∥b (2) a∥b (3) a与b相交
6. (1) 一条
(2) 平行
7. (1) 略 (2) 略
(3) l1,l2的夹角与∠O相等或互补.
8. D 9. B 10. C 11. D 12. 3
13. (1) (答案不唯一)正面:AB∥EF;上面:A′B′∥AB;右面:DD′∥HR
(2) EF∥A′B′
14. (1) 如图,点M,点N即为所求.
(2) 四边形PMAN的面积为5×7-×3×3-×2×4-×3×3-×2×4=18.
15. 由图可知,
有一条直线时,最多分成2部分;
有两条直线时,最多分成2+2=4部分;
有三条直线时,最多分成1+1+2+3=7部分;
设有n条直线,分成的平面最多有m个,则
m=1+1+…+(n-1)+n=n(n+1)+1,
当n=10时,×10×11+1=56,
故10条直线最多可以将平面分成56个部分.
第2课时 平行线的判定——同位角
1. B 2. D 3. D 4. l3 l4 l1 ∠1,∠5
5. 15° 6. 同位角相等,两直线平行
7. 平行,理由如下:
因为AC⊥AE,BD⊥BF,∠1=∠2,
所以∠EAB=∠FBQ,
所以AE∥BF(同位角相等,两直线平行).
8. B 9. B 10. 3 11. 3或21或75或165
12. 因为EF⊥FG,
所以∠EFG=90°,
即∠EFD+∠2=90°.
又因为∠1+∠2=90°,
所以∠EFD=∠1,
所以AB∥CD.
13. (1) 如图,直线m即为所求.
(2) 如图,直线m即为所求.
第3课时 平行线的判定——内错角、同旁内角
1. C 2. D
3. (1) DE BC AB 同位 (2) ∠4 (3) ∠BFA AB AF BC或∠BED ED BC AB (4) AB AF DE 内错
4. ∠1=∠A(答案不唯一)
5. (1) AB CD 内错角相等,两直线平行
(2) BCD 同旁内角互补,两直线平行
(3) 2 内错角相等,两直线平行
(4) ABC 同位角相等,两直线平行
6. 2 ECD 角平分线的定义
ECD 等量代换
内错角相等,两直线平行
7. D 8. B 9. 30°或150° 10. 或
11. 因为BD平分∠ABC,
所以∠DBF=∠ABC.
因为CE平分∠ACB,
所以∠ECB=∠ACB.
因为∠ABC=∠ACB,
所以∠DBF=∠ECB.
因为∠DBF=∠F,
所以∠ECB=∠F,
所以EC∥DF.
12. (1) 当∠1+∠2=90°时,AB∥CD,理由如下:
因为EG平分∠BEF,FH平分∠DFE,
所以∠BEF=2∠1,∠DFE=2∠2.
因为∠1+∠2=90°,
所以∠BEF+∠DFE=180°,
所以AB∥CD.
(2) 当∠1=∠2时,AB∥CD,理由如下:
因为EG平分∠BEM,FH平分∠DFE,
所以∠BEM=2∠1,∠DFE=2∠2.
因为∠1=∠2,
所以∠BEM=∠DFE,
所以AB∥CD.
(3) 当∠1=∠2时,AB∥CD,理由如下:
因为EG平分∠AEF,FH平分∠DFE,
所以∠AEF=2∠1,∠DFE=2∠2.
因为∠1=∠2,
所以∠AEF=∠DFE,
所以AB∥CD.
第4课时 平行线的性质
1. B 2. B 3. B 4. B 5. 105° 6. 100°
7. 因为AE∥BD,∠EAB=130°,∠EFD=30°,
所以∠CBD=130°,∠CFB=30°,
所以∠C=180°-∠CBD-∠CFB=180°-130°-30°=20°.
8. C 9. C 10. 152° 11. 56°
12. 因为EF∥AD,
所以∠2=∠3.
因为∠1=∠2,
所以∠1=∠3,
所以DG∥AB,
所以∠BAC+∠AGD=180°.
因为∠BAC=70°,所以∠AGD=110°.
13. (1) 因为AC∥EF,
所以∠1+∠FAC=180°.
因为∠1+∠2=180°,
所以∠FAC=∠2,
所以FA∥CD,
所以∠FAB=∠BDC.
(2) 因为AC平分∠FAD,
所以∠FAC=∠CAD,∠FAD=2∠FAC.
由(1)知∠FAC=∠2,
所以∠FAD=2∠2,
所以∠2=∠FAD.
因为∠FAD=80°,
所以∠2=×80°=40°.
因为EF⊥BE,AC∥EF,
所以AC⊥BE,
所以∠ACB=90°,
所以∠BCD=90°-∠2=50°.
同课章节目录
