6.5 多边形 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 6.5 多边形 同步练(含答案)2025-2026学年数学苏科版(2024)七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览

文档简介
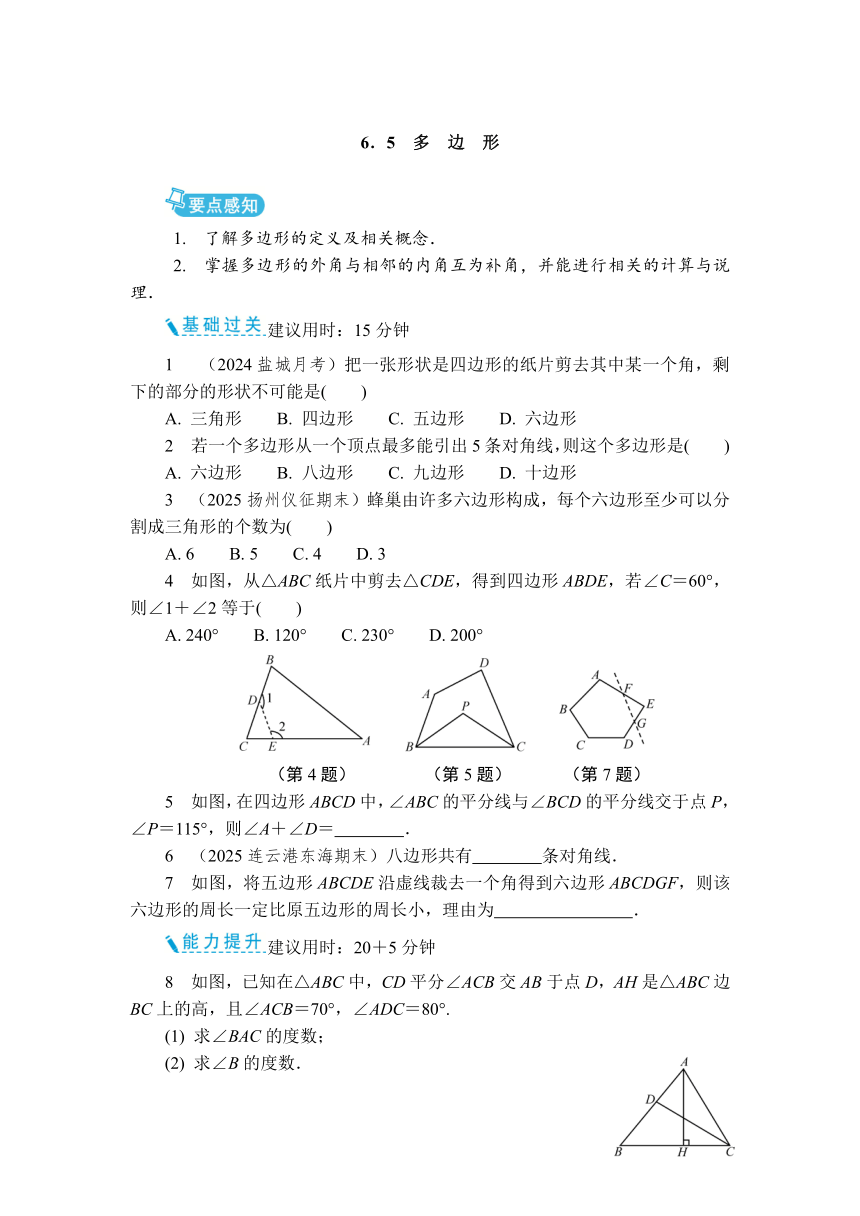
6.5 多 边 形
1. 了解多边形的定义及相关概念.
2. 掌握多边形的外角与相邻的内角互为补角,并能进行相关的计算与说理.
建议用时:15分钟
1 (2024盐城月考)把一张形状是四边形的纸片剪去其中某一个角,剩下的部分的形状不可能是( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
2 若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A. 六边形 B. 八边形 C. 九边形 D. 十边形
3 (2025扬州仪征期末)蜂巢由许多六边形构成,每个六边形至少可以分割成三角形的个数为( )
A. 6 B. 5 C. 4 D. 3
4 如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°,则∠1+∠2等于( )
A. 240° B. 120° C. 230° D. 200°
(第4题) (第5题) (第7题)
5 如图,在四边形ABCD中,∠ABC的平分线与∠BCD的平分线交于点P,∠P=115°,则∠A+∠D= .
6 (2025连云港东海期末)八边形共有 条对角线.
7 如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由为 .
建议用时:20+5分钟
8 如图,已知在△ABC中,CD平分∠ACB交AB于点D,AH是△ABC边BC上的高,且∠ACB=70°,∠ADC=80°.
(1) 求∠BAC的度数;
(2) 求∠B的度数.
9 如图,点D在线段BC的延长线上,过点B作射线BF交AC于点E,则下列是△ABE外角的是( )
A. ∠ACD B. ∠AEB C. ∠AEF D. ∠CEF
(第9题) (第10题)
10 (教材P195习题2变式)完美五边形是指可以无重叠、无间隙铺满整个平面的凸五边形.展示了数学与艺术的完美结合,它不仅是数学领域中的一个重要发现,还在建筑设计、艺术创作等领域中具有重要的美学价值.如图,五边形ABCDE是人类发现的第15种完美五边形的示意图,其中∠1+∠5=120°,则∠2+∠3+∠4等于( )
A. 145° B. 180° C. 240° D. 325°
11 已知一个多边形的边数恰好是从一个顶点出发的对角线条数的2倍,则这个多边形的边数是 .
12 如图,将三角形纸片ABC沿虚线剪掉两角得五边形CDEFG,若DE∥CG,FG∥CD,根据所标数据,求∠A的度数.
13 【观察思考】
如图,五边形ABCDE内部有若干个点,用这些点以及五边形ABCDE的顶点A,B,C,D,E把原五边形分割成一些三角形(互相不重叠).
内部有1个点 内部有2个点 内部有3个点
【规律总结】
(1) 填写下表:
五边形ABCDE内点的个数 1 2 3 4 … n
分割成的三角形的个数 5 7 9 …
【问题解决】
(2) 原五边形能否被分割成2 026个三角形?若能,求此时五边形ABCDE内部点的个数;若不能,请说明理由.
6.5 多 边 形
1. D 2. B 3. C 4. A 5. 230° 6. 20
7. 两点之间,线段最短
8. (1) 因为CD平分∠ACB,∠ACB=70°,
所以∠ACD=∠ACB=35°.
在△ACD中,∠ACD=35°,∠ADC=80°,
所以∠BAC=180°-∠ACD-∠ADC=180°-35°-80°=65°.
(2) 在△ABC中,∠BAC=65°,∠ACB=70°,
所以∠B=180°-∠BAC-∠ACB=180°-65°-70°=45°.
9. C 10. C 11. 6
12. 如图,根据题意得∠DEF=126°,∠FGC=118°,
所以∠AED=180°-126°=54°,∠BGF=180°-118°=62°.
因为DE∥CG,FG∥CD,
所以∠B=∠AED=54°,∠C=∠BGF=62°,
所以∠A=180°-∠B-∠C=64°.
13. (1) 11 2n+3
(2) 原五边形不能被分割成2 026个三角形,理由如下:
由题意,得2n+3=2 026,
解得n=1 011.5,不符合实际,
所以原五边形不能被分割成2 026个三角形.
1. 了解多边形的定义及相关概念.
2. 掌握多边形的外角与相邻的内角互为补角,并能进行相关的计算与说理.
建议用时:15分钟
1 (2024盐城月考)把一张形状是四边形的纸片剪去其中某一个角,剩下的部分的形状不可能是( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
2 若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A. 六边形 B. 八边形 C. 九边形 D. 十边形
3 (2025扬州仪征期末)蜂巢由许多六边形构成,每个六边形至少可以分割成三角形的个数为( )
A. 6 B. 5 C. 4 D. 3
4 如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°,则∠1+∠2等于( )
A. 240° B. 120° C. 230° D. 200°
(第4题) (第5题) (第7题)
5 如图,在四边形ABCD中,∠ABC的平分线与∠BCD的平分线交于点P,∠P=115°,则∠A+∠D= .
6 (2025连云港东海期末)八边形共有 条对角线.
7 如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由为 .
建议用时:20+5分钟
8 如图,已知在△ABC中,CD平分∠ACB交AB于点D,AH是△ABC边BC上的高,且∠ACB=70°,∠ADC=80°.
(1) 求∠BAC的度数;
(2) 求∠B的度数.
9 如图,点D在线段BC的延长线上,过点B作射线BF交AC于点E,则下列是△ABE外角的是( )
A. ∠ACD B. ∠AEB C. ∠AEF D. ∠CEF
(第9题) (第10题)
10 (教材P195习题2变式)完美五边形是指可以无重叠、无间隙铺满整个平面的凸五边形.展示了数学与艺术的完美结合,它不仅是数学领域中的一个重要发现,还在建筑设计、艺术创作等领域中具有重要的美学价值.如图,五边形ABCDE是人类发现的第15种完美五边形的示意图,其中∠1+∠5=120°,则∠2+∠3+∠4等于( )
A. 145° B. 180° C. 240° D. 325°
11 已知一个多边形的边数恰好是从一个顶点出发的对角线条数的2倍,则这个多边形的边数是 .
12 如图,将三角形纸片ABC沿虚线剪掉两角得五边形CDEFG,若DE∥CG,FG∥CD,根据所标数据,求∠A的度数.
13 【观察思考】
如图,五边形ABCDE内部有若干个点,用这些点以及五边形ABCDE的顶点A,B,C,D,E把原五边形分割成一些三角形(互相不重叠).
内部有1个点 内部有2个点 内部有3个点
【规律总结】
(1) 填写下表:
五边形ABCDE内点的个数 1 2 3 4 … n
分割成的三角形的个数 5 7 9 …
【问题解决】
(2) 原五边形能否被分割成2 026个三角形?若能,求此时五边形ABCDE内部点的个数;若不能,请说明理由.
6.5 多 边 形
1. D 2. B 3. C 4. A 5. 230° 6. 20
7. 两点之间,线段最短
8. (1) 因为CD平分∠ACB,∠ACB=70°,
所以∠ACD=∠ACB=35°.
在△ACD中,∠ACD=35°,∠ADC=80°,
所以∠BAC=180°-∠ACD-∠ADC=180°-35°-80°=65°.
(2) 在△ABC中,∠BAC=65°,∠ACB=70°,
所以∠B=180°-∠BAC-∠ACB=180°-65°-70°=45°.
9. C 10. C 11. 6
12. 如图,根据题意得∠DEF=126°,∠FGC=118°,
所以∠AED=180°-126°=54°,∠BGF=180°-118°=62°.
因为DE∥CG,FG∥CD,
所以∠B=∠AED=54°,∠C=∠BGF=62°,
所以∠A=180°-∠B-∠C=64°.
13. (1) 11 2n+3
(2) 原五边形不能被分割成2 026个三角形,理由如下:
由题意,得2n+3=2 026,
解得n=1 011.5,不符合实际,
所以原五边形不能被分割成2 026个三角形.
同课章节目录
