第5章走进几何世界 达标检测卷(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 第5章走进几何世界 达标检测卷(含答案)2025-2026学年数学苏科版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 19:41:10 | ||
图片预览

文档简介
第5章 走进几何世界 达标检测卷
(时间:120分钟 满分:120分)
班级:________姓名:________学号:________得分:________
一、 选择题(每小题3分,共30分)
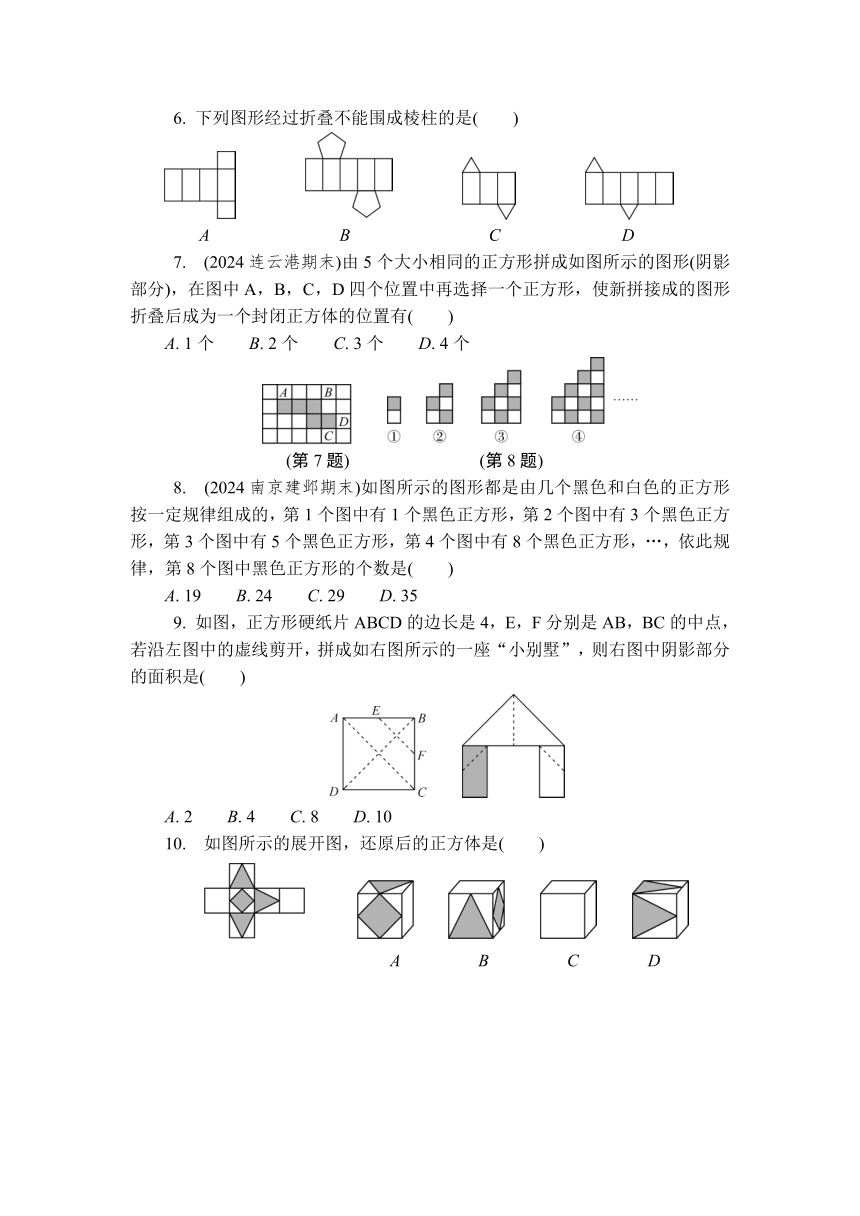
1. (2024镇江句容期末)如图为小文同学的几何体素描作品,该作品中不存在的几何体为( )
A. 棱柱 B. 球 C. 圆柱 D. 棱锥
2. 将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A. 96 B. 69 C. 66 D. 99
3. 如图是一个几何体的展开图,该几何体是( )
A. 圆柱 B. 三棱锥
C. 四棱柱 D. 三棱柱
4. 如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的几何体是( )
A B C D
5. 如图是一个几何体的侧面展开图,则该几何体是( )
A. 三棱柱 B. 三棱锥
C. 五棱柱 D. 五棱锥
6. 下列图形经过折叠不能围成棱柱的是( )
A B C D
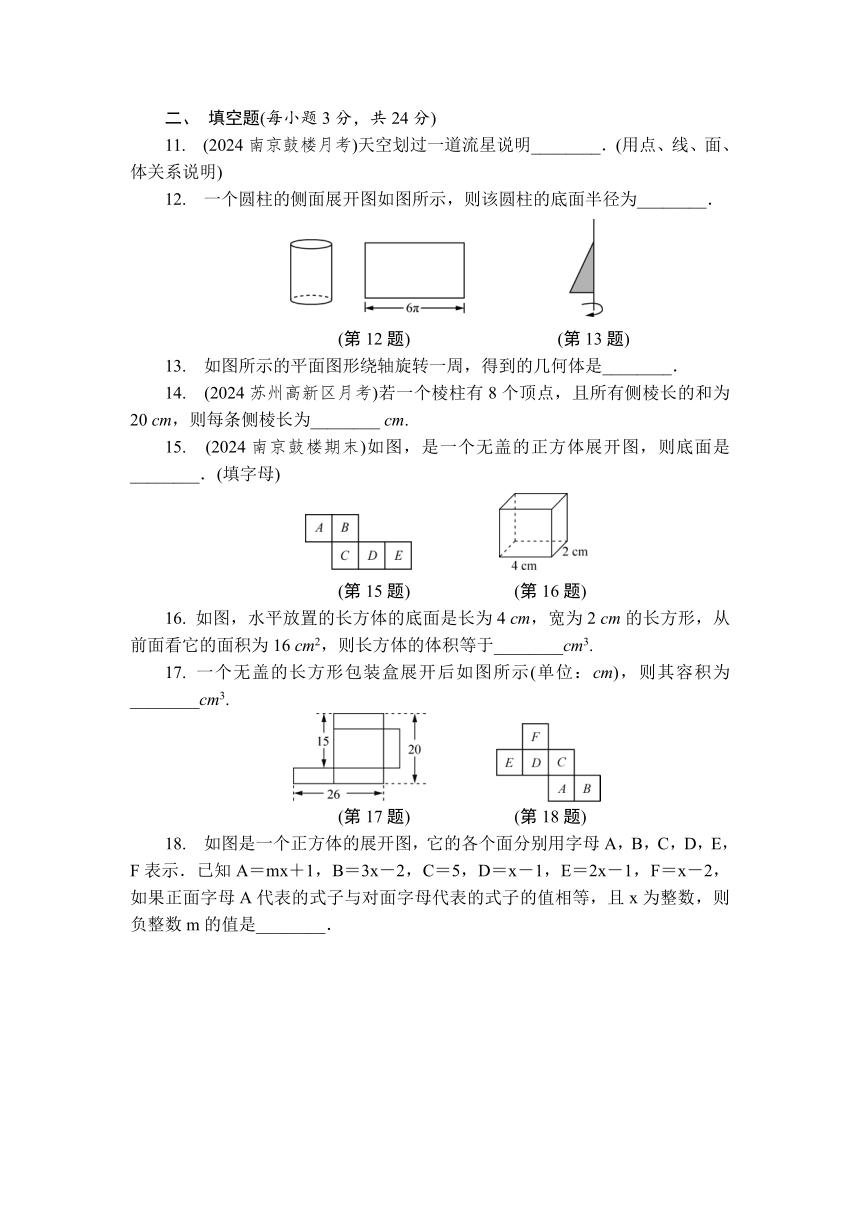
7. (2024连云港期末)由5个大小相同的正方形拼成如图所示的图形(阴影部分),在图中A,B,C,D四个位置中再选择一个正方形,使新拼接成的图形折叠后成为一个封闭正方体的位置有( )
A. 1个 B. 2个 C. 3个 D. 4个
(第7题) (第8题)
8. (2024南京建邺期末)如图所示的图形都是由几个黑色和白色的正方形按一定规律组成的,第1个图中有1个黑色正方形,第2个图中有3个黑色正方形,第3个图中有5个黑色正方形,第4个图中有8个黑色正方形,…,依此规律,第8个图中黑色正方形的个数是( )
A. 19 B. 24 C. 29 D. 35
9. 如图,正方形硬纸片ABCD的边长是4,E,F分别是AB,BC的中点,若沿左图中的虚线剪开,拼成如右图所示的一座“小别墅”,则右图中阴影部分的面积是( )
A. 2 B. 4 C. 8 D. 10
10. 如图所示的展开图,还原后的正方体是( )
A B C D
二、 填空题(每小题3分,共24分)
11. (2024南京鼓楼月考)天空划过一道流星说明________.(用点、线、面、体关系说明)
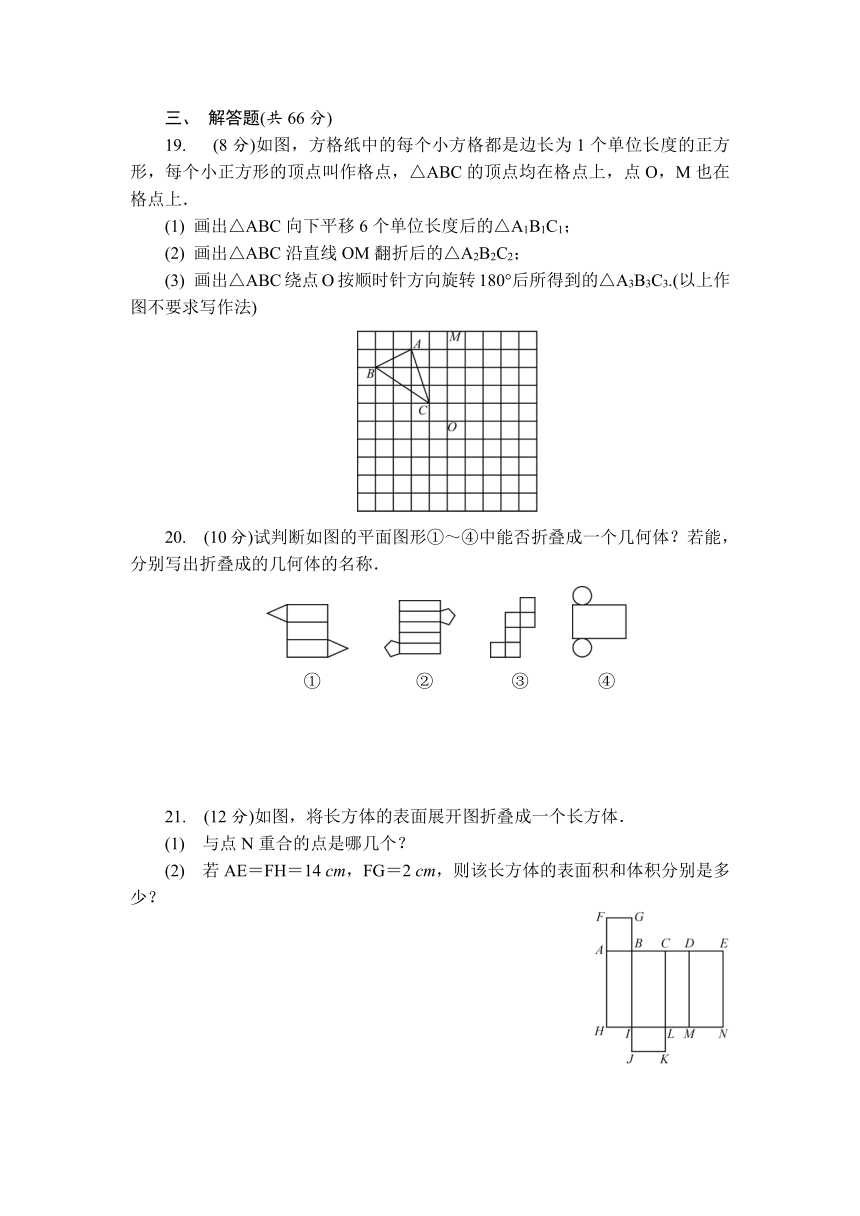
12. 一个圆柱的侧面展开图如图所示,则该圆柱的底面半径为________.
(第12题) (第13题)
13. 如图所示的平面图形绕轴旋转一周,得到的几何体是________.
14. (2024苏州高新区月考)若一个棱柱有8个顶点,且所有侧棱长的和为20 cm,则每条侧棱长为________ cm.
15. (2024南京鼓楼期末)如图,是一个无盖的正方体展开图,则底面是________.(填字母)
(第15题) (第16题)
16. 如图,水平放置的长方体的底面是长为4 cm,宽为2 cm的长方形,从前面看它的面积为16 cm2,则长方体的体积等于________cm3.
17. 一个无盖的长方形包装盒展开后如图所示(单位:cm),则其容积为________cm3.
(第17题) (第18题)
18. 如图是一个正方体的展开图,它的各个面分别用字母A,B,C,D,E,F表示.已知A=mx+1,B=3x-2,C=5,D=x-1,E=2x-1,F=x-2,如果正面字母A代表的式子与对面字母代表的式子的值相等,且x为整数,则负整数m的值是________.
三、 解答题(共66分)
19. (8分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫作格点,△ABC的顶点均在格点上,点O,M也在格点上.
(1) 画出△ABC向下平移6个单位长度后的△A1B1C1;
(2) 画出△ABC沿直线OM翻折后的△A2B2C2;
(3) 画出△ABC绕点O按顺时针方向旋转180°后所得到的△A3B3C3.(以上作图不要求写作法)
20. (10分)试判断如图的平面图形①~④中能否折叠成一个几何体?若能,分别写出折叠成的几何体的名称.
① ② ③ ④
21. (12分)如图,将长方体的表面展开图折叠成一个长方体.
(1) 与点N重合的点是哪几个?
(2) 若AE=FH=14 cm,FG=2 cm,则该长方体的表面积和体积分别是多少?
22. (12分)如图1是一个三角形,分别连接这个三角形三边的中点得到图2,再分别连接图2中间的小三角形三边中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,解答下列问题:
(1) 将下表填写完整:
图形编号 1 2 3 4 5
三角形个数 1 5
(2) 按照这样的规律,在第n个图形中有多少个三角形(用含n的式子表示)
(3) 按照这样的规律,在第100个图形里有多少个三角形?
(4) 按照这样的规律,当三角形个数为600时,如果能出现,出现在第几个图形里?如果不能出现,请说明理由.
图1 图2 图3
23. (12分)一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示.
(1) A的相对面是________,B的相对面是________,C的相对面是________;
(2) 若A=-5,B=|m-1|,C=m-4n-,E=,且小正方体各相对面上的两个数都互为相反数,试求出F所表示的数.
24. (12分)十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V),面数(F),棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下图中几种简单的多面体模型,并解答下列问题:
(1) 根据上面的多面体模型完成下表:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4
长方体 8 6 12
正八面体 8 12
正十二面体 20 12 30
则顶点数(V),面数(F),棱数(E)之间存在的关系式是____________;
(2) 若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是________;
(3) 某个玻璃饰品的外形是简单多面体,它的外表面由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.
第5章达标检测卷
1. D 2. B 3. D 4. A 5. D 6. D 7. B 8. B
9. B 10. D
11. 点动成线 12. 3 13. 圆锥 14. 5 15. B
16. 32 17. 800 18. -2
19. (1) 如图,△A1B1C1为所作.
(2) 如图,△A2B2C2为所作.
(3) 如图,△A3B3C3为所作.
20. 观察图形,由几何体及其表面展开图的特点可知:图①~④都能折叠成一个几何体,其中
①是三棱柱,②是五棱柱,③是正方体,④是圆柱.
21. (1) 与点N重合的点有点H和点J.
(2) 根据题意,得FG=AB=CD=2 cm,
所以AF=BC=DE=(14-2×2)÷2=5(cm),
所以AH=FH-AF=14-5=9(cm),
所以S=(9×5+5×2+9×2)×2=146(cm2),
所以V=2×5×9=90(cm3).
故该长方体的表面积和体积分别为146 cm2和90 cm3.
22. (1) 9 13 17
(2) 4n-3
(3) 当n=100时,4n-3=4×100-3=397(个),
所以在第100个图形里有397个三角形.
(4) 根据题意,得4n-3=600,
解得n=150.75.
因为n不是整数,
所以不能出现三角形个数为600个的图形.
23. (1) D E F
(2) 因为B面上的数与E面上的数互为相反数,
所以|m-1|+=0,
解得m=1,n=-,
所以C=m-4n-=9.5.
又C面上的数与F面上的数互为相反数,
故F所表示的数为-9.5.
24. (1) 6 6 V+F-E=2 (2) 20
(3) 根据题意,得E=24×3÷2=36.
由V+F-E=2,得24+F-36=2,
解得F=14,
所以x+y=14.
(时间:120分钟 满分:120分)
班级:________姓名:________学号:________得分:________
一、 选择题(每小题3分,共30分)
1. (2024镇江句容期末)如图为小文同学的几何体素描作品,该作品中不存在的几何体为( )
A. 棱柱 B. 球 C. 圆柱 D. 棱锥
2. 将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A. 96 B. 69 C. 66 D. 99
3. 如图是一个几何体的展开图,该几何体是( )
A. 圆柱 B. 三棱锥
C. 四棱柱 D. 三棱柱
4. 如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的几何体是( )
A B C D
5. 如图是一个几何体的侧面展开图,则该几何体是( )
A. 三棱柱 B. 三棱锥
C. 五棱柱 D. 五棱锥
6. 下列图形经过折叠不能围成棱柱的是( )
A B C D
7. (2024连云港期末)由5个大小相同的正方形拼成如图所示的图形(阴影部分),在图中A,B,C,D四个位置中再选择一个正方形,使新拼接成的图形折叠后成为一个封闭正方体的位置有( )
A. 1个 B. 2个 C. 3个 D. 4个
(第7题) (第8题)
8. (2024南京建邺期末)如图所示的图形都是由几个黑色和白色的正方形按一定规律组成的,第1个图中有1个黑色正方形,第2个图中有3个黑色正方形,第3个图中有5个黑色正方形,第4个图中有8个黑色正方形,…,依此规律,第8个图中黑色正方形的个数是( )
A. 19 B. 24 C. 29 D. 35
9. 如图,正方形硬纸片ABCD的边长是4,E,F分别是AB,BC的中点,若沿左图中的虚线剪开,拼成如右图所示的一座“小别墅”,则右图中阴影部分的面积是( )
A. 2 B. 4 C. 8 D. 10
10. 如图所示的展开图,还原后的正方体是( )
A B C D
二、 填空题(每小题3分,共24分)
11. (2024南京鼓楼月考)天空划过一道流星说明________.(用点、线、面、体关系说明)
12. 一个圆柱的侧面展开图如图所示,则该圆柱的底面半径为________.
(第12题) (第13题)
13. 如图所示的平面图形绕轴旋转一周,得到的几何体是________.
14. (2024苏州高新区月考)若一个棱柱有8个顶点,且所有侧棱长的和为20 cm,则每条侧棱长为________ cm.
15. (2024南京鼓楼期末)如图,是一个无盖的正方体展开图,则底面是________.(填字母)
(第15题) (第16题)
16. 如图,水平放置的长方体的底面是长为4 cm,宽为2 cm的长方形,从前面看它的面积为16 cm2,则长方体的体积等于________cm3.
17. 一个无盖的长方形包装盒展开后如图所示(单位:cm),则其容积为________cm3.
(第17题) (第18题)
18. 如图是一个正方体的展开图,它的各个面分别用字母A,B,C,D,E,F表示.已知A=mx+1,B=3x-2,C=5,D=x-1,E=2x-1,F=x-2,如果正面字母A代表的式子与对面字母代表的式子的值相等,且x为整数,则负整数m的值是________.
三、 解答题(共66分)
19. (8分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫作格点,△ABC的顶点均在格点上,点O,M也在格点上.
(1) 画出△ABC向下平移6个单位长度后的△A1B1C1;
(2) 画出△ABC沿直线OM翻折后的△A2B2C2;
(3) 画出△ABC绕点O按顺时针方向旋转180°后所得到的△A3B3C3.(以上作图不要求写作法)
20. (10分)试判断如图的平面图形①~④中能否折叠成一个几何体?若能,分别写出折叠成的几何体的名称.
① ② ③ ④
21. (12分)如图,将长方体的表面展开图折叠成一个长方体.
(1) 与点N重合的点是哪几个?
(2) 若AE=FH=14 cm,FG=2 cm,则该长方体的表面积和体积分别是多少?
22. (12分)如图1是一个三角形,分别连接这个三角形三边的中点得到图2,再分别连接图2中间的小三角形三边中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,解答下列问题:
(1) 将下表填写完整:
图形编号 1 2 3 4 5
三角形个数 1 5
(2) 按照这样的规律,在第n个图形中有多少个三角形(用含n的式子表示)
(3) 按照这样的规律,在第100个图形里有多少个三角形?
(4) 按照这样的规律,当三角形个数为600时,如果能出现,出现在第几个图形里?如果不能出现,请说明理由.
图1 图2 图3
23. (12分)一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示.
(1) A的相对面是________,B的相对面是________,C的相对面是________;
(2) 若A=-5,B=|m-1|,C=m-4n-,E=,且小正方体各相对面上的两个数都互为相反数,试求出F所表示的数.
24. (12分)十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V),面数(F),棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下图中几种简单的多面体模型,并解答下列问题:
(1) 根据上面的多面体模型完成下表:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4
长方体 8 6 12
正八面体 8 12
正十二面体 20 12 30
则顶点数(V),面数(F),棱数(E)之间存在的关系式是____________;
(2) 若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是________;
(3) 某个玻璃饰品的外形是简单多面体,它的外表面由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.
第5章达标检测卷
1. D 2. B 3. D 4. A 5. D 6. D 7. B 8. B
9. B 10. D
11. 点动成线 12. 3 13. 圆锥 14. 5 15. B
16. 32 17. 800 18. -2
19. (1) 如图,△A1B1C1为所作.
(2) 如图,△A2B2C2为所作.
(3) 如图,△A3B3C3为所作.
20. 观察图形,由几何体及其表面展开图的特点可知:图①~④都能折叠成一个几何体,其中
①是三棱柱,②是五棱柱,③是正方体,④是圆柱.
21. (1) 与点N重合的点有点H和点J.
(2) 根据题意,得FG=AB=CD=2 cm,
所以AF=BC=DE=(14-2×2)÷2=5(cm),
所以AH=FH-AF=14-5=9(cm),
所以S=(9×5+5×2+9×2)×2=146(cm2),
所以V=2×5×9=90(cm3).
故该长方体的表面积和体积分别为146 cm2和90 cm3.
22. (1) 9 13 17
(2) 4n-3
(3) 当n=100时,4n-3=4×100-3=397(个),
所以在第100个图形里有397个三角形.
(4) 根据题意,得4n-3=600,
解得n=150.75.
因为n不是整数,
所以不能出现三角形个数为600个的图形.
23. (1) D E F
(2) 因为B面上的数与E面上的数互为相反数,
所以|m-1|+=0,
解得m=1,n=-,
所以C=m-4n-=9.5.
又C面上的数与F面上的数互为相反数,
故F所表示的数为-9.5.
24. (1) 6 6 V+F-E=2 (2) 20
(3) 根据题意,得E=24×3÷2=36.
由V+F-E=2,得24+F-36=2,
解得F=14,
所以x+y=14.
同课章节目录
