第6章平面图形的初步认识 达标检测卷(含答案)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 第6章平面图形的初步认识 达标检测卷(含答案)2025-2026学年数学苏科版(2024)七年级上册 | 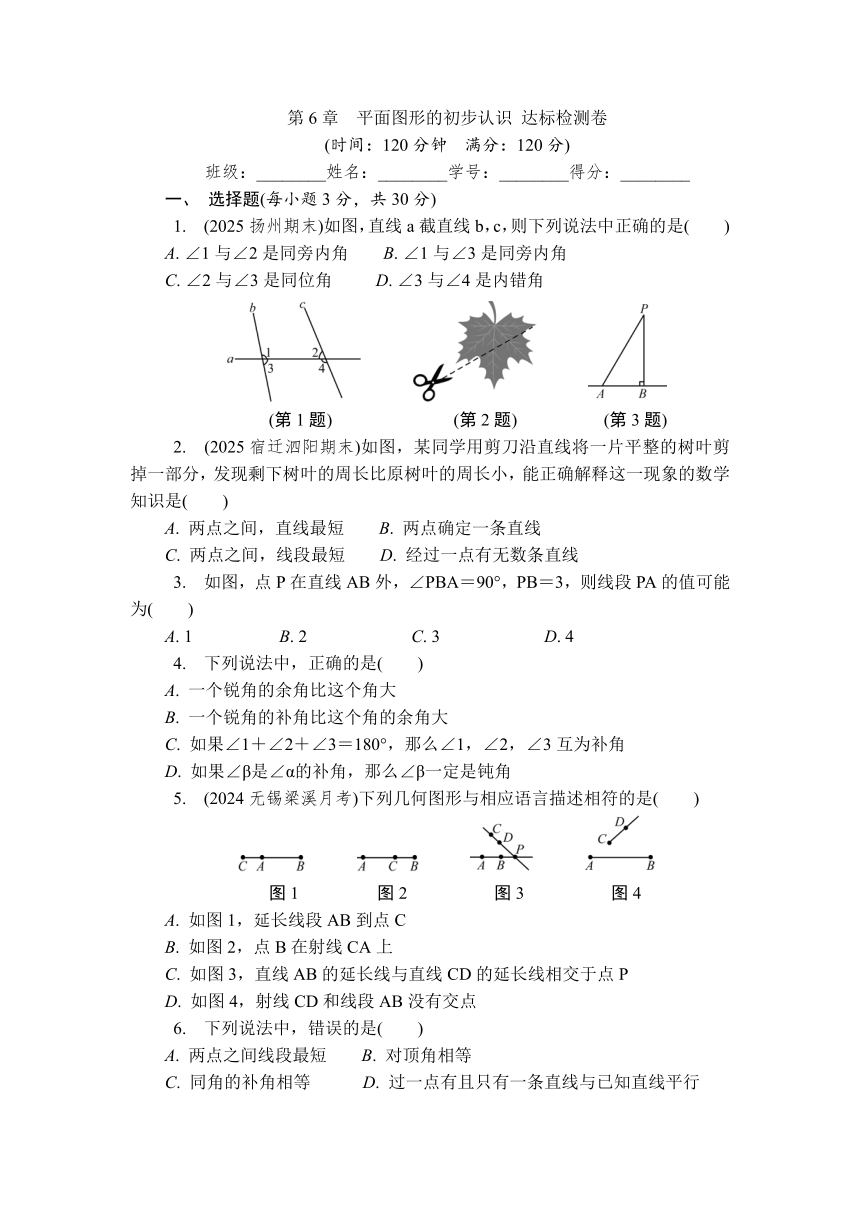 | |
| 格式 | docx | ||
| 文件大小 | 275.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 19:41:50 | ||
图片预览




文档简介
第6章 平面图形的初步认识 达标检测卷
(时间:120分钟 满分:120分)
班级:________姓名:________学号:________得分:________
一、 选择题(每小题3分,共30分)
1. (2025扬州期末)如图,直线a截直线b,c,则下列说法中正确的是( )
A. ∠1与∠2是同旁内角 B. ∠1与∠3是同旁内角
C. ∠2与∠3是同位角 D. ∠3与∠4是内错角
(第1题) (第2题) (第3题)
2. (2025宿迁泗阳期末)如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
A. 两点之间,直线最短 B. 两点确定一条直线
C. 两点之间,线段最短 D. 经过一点有无数条直线
3. 如图,点P在直线AB外,∠PBA=90°,PB=3,则线段PA的值可能为( )
A. 1 B. 2 C. 3 D. 4
4. 下列说法中,正确的是( )
A. 一个锐角的余角比这个角大
B. 一个锐角的补角比这个角的余角大
C. 如果∠1+∠2+∠3=180°,那么∠1,∠2,∠3互为补角
D. 如果∠β是∠α的补角,那么∠β一定是钝角
5. (2024无锡梁溪月考)下列几何图形与相应语言描述相符的是( )
图1 图2 图3 图4
A. 如图1,延长线段AB到点C
B. 如图2,点B在射线CA上
C. 如图3,直线AB的延长线与直线CD的延长线相交于点P
D. 如图4,射线CD和线段AB没有交点
6. 下列说法中,错误的是( )
A. 两点之间线段最短 B. 对顶角相等
C. 同角的补角相等 D. 过一点有且只有一条直线与已知直线平行
7. 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A. ∠3=∠4 B. ∠D+∠ACD=180°
C. ∠D=∠DCE D. ∠1=∠2
8. 如图,M是线段AB的中点,NB为MB的,MN=a,则AB的长为( )
A. a B. a C. 2a D. 1.5a
9. (2024南通通州月考)如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=60°,则∠BOF的度数是( )
A. 50° B. 60° C. 65° D. 55°
(第9题) (第10题)
10. (2024常州期末)将一块含30°角的直角三角板与一把直尺按如图所示方式摆放,∠C=90°,∠A=30°.若∠1=α°,则∠3-∠2的大小为( )
A. 30° B. 60°
C. (30+α)° D. (30+2α)°
二、 填空题(每小题3分,共24分)
11. (2024巴中)从五边形的一个顶点出发可以引________条对角线.
12. 在墙上固定一根木棒时,至少需要两根钉子,其中所体现的基本事实是____________.
13. (2024南京玄武月考)比较大小:25°15′________25.15°.(填“>”“<”或“=”)
14. 如图,线段AB=8,C是线段AB的中点,点D在CB上,DB=1.5,则线段CD的长等于________.
(第14题) (第17题) (第18题)
15. 已知直线上有A,B,C三点,AB=4,BC=6,则AC=________.
16. (2024南京建邺开学考试)12:10时针和分针所夹的较小角的度数为________.
17. 如图是一款长臂折叠LED护眼灯示意图,EF与桌面MN垂直,当发光的灯管AB恰好与桌面MN平行时,∠DEF=120°,∠BCD=110°,则∠CDE的度数为________.
18. 将一副标准三角板中的两个直角顶点C按如图方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°),当ACE<180°,且点E在直线AC的上方时,满足△BCE有一条边与斜边AD平行,则此时∠ACE=________.
三、 解答题(共66分)
19. (6分) 如图,已知四点A,B,C,D,请用尺规作图.(保留作图痕迹)
(1) 画直线AB;
(2) 画射线AC;
(3) 连接BC并延长至点F,使得CF=AB,比较AC与BF的大小:________;
(4) 在直线AC上确定一点E,使它到点D,B的距离之和最小.
20. (8分)(2025南京浦口月考)请把下列说理过程及理由补充完整.
已知:如图,∠1=∠2,∠B=∠C.
求证:∠B+∠BFC=180°.
证明:因为∠1=∠2(已知),
且∠1=∠CGD(____________),
所以∠2=∠CGD(等量代换).
所以CE∥BF(________________________),
所以________=∠C(____________________).
因为∠B=∠C(已知),
所以∠BFD=∠B(____________________),
所以AB∥CD(______________________),
所以∠B+∠BFC=180°(____________).
21. (8分)(2024泰州月考)如图,BD平分∠ABC,∠C=30°,∠ABD=75°,AE,BD交于点F.
(1) 求证:AB∥CD;
(2) 若AE∥BC,求________的度数.
请从“①∠AFD;②∠A”中选择一项填在上面横线处(填序号),并写出求解过程.
22. (10分)如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2∶∠1=4∶1.
(1) 求∠AOF的大小;
(2) 判断OE与OF的位置关系,并说明理由.
23. (10分)已知线段AB=12,线段CD=6,线段CD在直线AB上运动(点A在点B的左侧,点C在点D的左侧).
(1) M,N分别是线段AC,BD的中点,若线段BC=4,求线段MN的长度;
(2) 当CD运动到点D与点B重合时,P是线段AB延长线上的一点,下列两个结论:①是定值;②是定值,请作出正确的选择,并求出其定值.
24. (10分)如图,直线AB,CD相交于点O.
(1) 如图1,若∠AOC=30°,则∠BOC=________,∠BOD=________;
(2) 如图2,将直线CD绕点O旋转,请根据下表所给数据将表格补充完整;
∠AOC 60° 90° x°
∠BOD ________ ________ ________
(3) 如图3,过点O分别作∠AOC与∠AOD的平分线OE,OF,若∠BOD的大小为α,请用含α的代数式表示∠COF的大小.
图1 图2 图3
25. (14分)数轴上A,B两点对应的数分别是-4,12,线段CE在数轴上运动,点C在点E的左边,且CE=8,F是AE的中点.
(1) 如图1,当线段CE运动到点C,E均在点A,B之间时,若CF=1,则AC=________,BE=________;
(2) 当线段CE运动到点A在点C,E之间时.
①设AF的长为x,用含x的代数式表示BE=________;
②求BE与CF的数量关系;
(3) 当点C运动到数轴上表示数-14的位置时,动点P从点E出发,以每秒3个单位长度的速度向右运动,抵达点B后,立即以每秒2个单位长度的速度返回;动点P出发时,点Q从点A出发,以每秒2个单位长度的速度向终点B运动;当点Q到达点B时,P,Q两点都停止,设它们运动的时间为t s,求t为何值时,P,Q两点间的距离为1个单位长度.
图1 备用图
第6章达标检测卷
1. A 2. C 3. D 4. B 5. D 6. D 7. D 8. A
9. B 10. D
11. 2 12. 两点确定一条直线 13. > 14. 2.5 15. 10或2 16. 55° 17. 100°
18. 30°或120°或165°
19. (1) 如图,直线AB即为所画的直线.
(2) 如图,射线AC即为所画的射线.
(3) 如图,线段CF即为所画的线段.
BF>AC
(4) 如图,E为AC,BD的交点.
20. 对顶角相等
同位角相等,两直线平行
∠BFD 两直线平行,同位角相等
等量代换
内错角相等,两直线平行
两直线平行,同旁内角互补
21. (1) 因为BD平分∠ABC,∠ABD=75°,
所以∠ABC=2∠DBC=2∠ABD=150°.
因为∠C=30°,
所以∠C+∠ABC=180°,
所以AB∥CD.
(2) 若选①:因为BD平分∠ABC,∠ABD=75°,
所以∠DBC=∠ABD=75°.
因为AE∥BC,
所以∠DFE=∠DBC=75°,
所以∠AFD=180°-75°=105°.
若选②:因为AE∥BC,
所以∠ABC+∠A=180°.
又∠ABC=150°,
所以∠A=180°-150°=30°.
22. (1) 因为OE平分∠BOD,OF平分∠BOC,
所以∠1=∠BOE=∠BOD,∠2=∠BOF=∠BOC.
又因为∠BOC+∠BOD=180°,∠2∶∠1=4∶1,
所以∠1=180°×=18°,∠2=180°×=72°,
所以∠AOC=∠BOD=2∠1=36°,
所以∠AOF=∠AOC+∠2=36°+72°=108°.
(2) OE⊥OF,理由如下:
因为OE平分∠BOD,OF平分∠BOC,
所以∠1=∠BOE=∠BOD,∠2=∠BOF=∠BOC.
又因为∠BOC+∠BOD=180°,
所以∠BOE+∠BOF=×(∠BOC+∠BOD)=×180°=90°,
所以OE⊥OF.
23. (1) 如图1,因为M,N分别为线段AC,BD的中点,
所以AM=AC=(AB+BC)=8,
DN=BD=(CD+BC)=5,
所以MN=AD-AM-DN=12+4+6-8-5=9;
如图2,因为M,N分别为线段AC,BD的中点,
所以AM=AC=(AB-BC)=4,
DN=BD=(CD-BC)=1,
所以MN=AD-AM-DN=12+6-4-4-1=9.
综上,线段MN的长度为9.
图1 图2
(2) ①正确,=2,理由如下:
由题意,得当CD运动到点D与点B重合时,AC=BC,
所以===2,
所以是定值2.
24. (1) 150° 30°
(2) 60° 90° x°
(3) 因为∠AOC=∠BOD=α,OE平分∠AOC,
所以∠EOC=α.
因为OF平分∠AOD,
所以∠AOF=∠AOD,
所以∠EOF=∠AOE+∠AOF=(∠AOC+∠AOD)=90°,
所以∠COF=∠EOC+∠EOF=90°+α.
25. (1) 6 2
(2) ①16-2x
②因为CF=CE-EF=CE-AF=8-x,
所以BE=2CF.
(3) 因为点C运动到数轴上表示数-14的位置,CE=8,
所以点E表示的数为-6.
当点P向数轴正方向运动,且与点Q没有相遇时,
由题意,得3t+1=2t+2,解得t=1;
当点P向数轴正方向运动,且与点Q相遇后时,
由题意,得3t-1=2t+2,解得t=3;
当点P向数轴负方向运动,且与点Q没有相遇时,
由题意,得2(t-6)+1+2t=16,解得t=;
当点P向数轴负方向运动,且与点Q相遇后时,
由题意,得2(t-6)+2t=16+1,解得t=.
综上,当t的值为1或3或或时,P,Q两点间的距离为1个单位长度.
(时间:120分钟 满分:120分)
班级:________姓名:________学号:________得分:________
一、 选择题(每小题3分,共30分)
1. (2025扬州期末)如图,直线a截直线b,c,则下列说法中正确的是( )
A. ∠1与∠2是同旁内角 B. ∠1与∠3是同旁内角
C. ∠2与∠3是同位角 D. ∠3与∠4是内错角
(第1题) (第2题) (第3题)
2. (2025宿迁泗阳期末)如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
A. 两点之间,直线最短 B. 两点确定一条直线
C. 两点之间,线段最短 D. 经过一点有无数条直线
3. 如图,点P在直线AB外,∠PBA=90°,PB=3,则线段PA的值可能为( )
A. 1 B. 2 C. 3 D. 4
4. 下列说法中,正确的是( )
A. 一个锐角的余角比这个角大
B. 一个锐角的补角比这个角的余角大
C. 如果∠1+∠2+∠3=180°,那么∠1,∠2,∠3互为补角
D. 如果∠β是∠α的补角,那么∠β一定是钝角
5. (2024无锡梁溪月考)下列几何图形与相应语言描述相符的是( )
图1 图2 图3 图4
A. 如图1,延长线段AB到点C
B. 如图2,点B在射线CA上
C. 如图3,直线AB的延长线与直线CD的延长线相交于点P
D. 如图4,射线CD和线段AB没有交点
6. 下列说法中,错误的是( )
A. 两点之间线段最短 B. 对顶角相等
C. 同角的补角相等 D. 过一点有且只有一条直线与已知直线平行
7. 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A. ∠3=∠4 B. ∠D+∠ACD=180°
C. ∠D=∠DCE D. ∠1=∠2
8. 如图,M是线段AB的中点,NB为MB的,MN=a,则AB的长为( )
A. a B. a C. 2a D. 1.5a
9. (2024南通通州月考)如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=60°,则∠BOF的度数是( )
A. 50° B. 60° C. 65° D. 55°
(第9题) (第10题)
10. (2024常州期末)将一块含30°角的直角三角板与一把直尺按如图所示方式摆放,∠C=90°,∠A=30°.若∠1=α°,则∠3-∠2的大小为( )
A. 30° B. 60°
C. (30+α)° D. (30+2α)°
二、 填空题(每小题3分,共24分)
11. (2024巴中)从五边形的一个顶点出发可以引________条对角线.
12. 在墙上固定一根木棒时,至少需要两根钉子,其中所体现的基本事实是____________.
13. (2024南京玄武月考)比较大小:25°15′________25.15°.(填“>”“<”或“=”)
14. 如图,线段AB=8,C是线段AB的中点,点D在CB上,DB=1.5,则线段CD的长等于________.
(第14题) (第17题) (第18题)
15. 已知直线上有A,B,C三点,AB=4,BC=6,则AC=________.
16. (2024南京建邺开学考试)12:10时针和分针所夹的较小角的度数为________.
17. 如图是一款长臂折叠LED护眼灯示意图,EF与桌面MN垂直,当发光的灯管AB恰好与桌面MN平行时,∠DEF=120°,∠BCD=110°,则∠CDE的度数为________.
18. 将一副标准三角板中的两个直角顶点C按如图方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°),当ACE<180°,且点E在直线AC的上方时,满足△BCE有一条边与斜边AD平行,则此时∠ACE=________.
三、 解答题(共66分)
19. (6分) 如图,已知四点A,B,C,D,请用尺规作图.(保留作图痕迹)
(1) 画直线AB;
(2) 画射线AC;
(3) 连接BC并延长至点F,使得CF=AB,比较AC与BF的大小:________;
(4) 在直线AC上确定一点E,使它到点D,B的距离之和最小.
20. (8分)(2025南京浦口月考)请把下列说理过程及理由补充完整.
已知:如图,∠1=∠2,∠B=∠C.
求证:∠B+∠BFC=180°.
证明:因为∠1=∠2(已知),
且∠1=∠CGD(____________),
所以∠2=∠CGD(等量代换).
所以CE∥BF(________________________),
所以________=∠C(____________________).
因为∠B=∠C(已知),
所以∠BFD=∠B(____________________),
所以AB∥CD(______________________),
所以∠B+∠BFC=180°(____________).
21. (8分)(2024泰州月考)如图,BD平分∠ABC,∠C=30°,∠ABD=75°,AE,BD交于点F.
(1) 求证:AB∥CD;
(2) 若AE∥BC,求________的度数.
请从“①∠AFD;②∠A”中选择一项填在上面横线处(填序号),并写出求解过程.
22. (10分)如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2∶∠1=4∶1.
(1) 求∠AOF的大小;
(2) 判断OE与OF的位置关系,并说明理由.
23. (10分)已知线段AB=12,线段CD=6,线段CD在直线AB上运动(点A在点B的左侧,点C在点D的左侧).
(1) M,N分别是线段AC,BD的中点,若线段BC=4,求线段MN的长度;
(2) 当CD运动到点D与点B重合时,P是线段AB延长线上的一点,下列两个结论:①是定值;②是定值,请作出正确的选择,并求出其定值.
24. (10分)如图,直线AB,CD相交于点O.
(1) 如图1,若∠AOC=30°,则∠BOC=________,∠BOD=________;
(2) 如图2,将直线CD绕点O旋转,请根据下表所给数据将表格补充完整;
∠AOC 60° 90° x°
∠BOD ________ ________ ________
(3) 如图3,过点O分别作∠AOC与∠AOD的平分线OE,OF,若∠BOD的大小为α,请用含α的代数式表示∠COF的大小.
图1 图2 图3
25. (14分)数轴上A,B两点对应的数分别是-4,12,线段CE在数轴上运动,点C在点E的左边,且CE=8,F是AE的中点.
(1) 如图1,当线段CE运动到点C,E均在点A,B之间时,若CF=1,则AC=________,BE=________;
(2) 当线段CE运动到点A在点C,E之间时.
①设AF的长为x,用含x的代数式表示BE=________;
②求BE与CF的数量关系;
(3) 当点C运动到数轴上表示数-14的位置时,动点P从点E出发,以每秒3个单位长度的速度向右运动,抵达点B后,立即以每秒2个单位长度的速度返回;动点P出发时,点Q从点A出发,以每秒2个单位长度的速度向终点B运动;当点Q到达点B时,P,Q两点都停止,设它们运动的时间为t s,求t为何值时,P,Q两点间的距离为1个单位长度.
图1 备用图
第6章达标检测卷
1. A 2. C 3. D 4. B 5. D 6. D 7. D 8. A
9. B 10. D
11. 2 12. 两点确定一条直线 13. > 14. 2.5 15. 10或2 16. 55° 17. 100°
18. 30°或120°或165°
19. (1) 如图,直线AB即为所画的直线.
(2) 如图,射线AC即为所画的射线.
(3) 如图,线段CF即为所画的线段.
BF>AC
(4) 如图,E为AC,BD的交点.
20. 对顶角相等
同位角相等,两直线平行
∠BFD 两直线平行,同位角相等
等量代换
内错角相等,两直线平行
两直线平行,同旁内角互补
21. (1) 因为BD平分∠ABC,∠ABD=75°,
所以∠ABC=2∠DBC=2∠ABD=150°.
因为∠C=30°,
所以∠C+∠ABC=180°,
所以AB∥CD.
(2) 若选①:因为BD平分∠ABC,∠ABD=75°,
所以∠DBC=∠ABD=75°.
因为AE∥BC,
所以∠DFE=∠DBC=75°,
所以∠AFD=180°-75°=105°.
若选②:因为AE∥BC,
所以∠ABC+∠A=180°.
又∠ABC=150°,
所以∠A=180°-150°=30°.
22. (1) 因为OE平分∠BOD,OF平分∠BOC,
所以∠1=∠BOE=∠BOD,∠2=∠BOF=∠BOC.
又因为∠BOC+∠BOD=180°,∠2∶∠1=4∶1,
所以∠1=180°×=18°,∠2=180°×=72°,
所以∠AOC=∠BOD=2∠1=36°,
所以∠AOF=∠AOC+∠2=36°+72°=108°.
(2) OE⊥OF,理由如下:
因为OE平分∠BOD,OF平分∠BOC,
所以∠1=∠BOE=∠BOD,∠2=∠BOF=∠BOC.
又因为∠BOC+∠BOD=180°,
所以∠BOE+∠BOF=×(∠BOC+∠BOD)=×180°=90°,
所以OE⊥OF.
23. (1) 如图1,因为M,N分别为线段AC,BD的中点,
所以AM=AC=(AB+BC)=8,
DN=BD=(CD+BC)=5,
所以MN=AD-AM-DN=12+4+6-8-5=9;
如图2,因为M,N分别为线段AC,BD的中点,
所以AM=AC=(AB-BC)=4,
DN=BD=(CD-BC)=1,
所以MN=AD-AM-DN=12+6-4-4-1=9.
综上,线段MN的长度为9.
图1 图2
(2) ①正确,=2,理由如下:
由题意,得当CD运动到点D与点B重合时,AC=BC,
所以===2,
所以是定值2.
24. (1) 150° 30°
(2) 60° 90° x°
(3) 因为∠AOC=∠BOD=α,OE平分∠AOC,
所以∠EOC=α.
因为OF平分∠AOD,
所以∠AOF=∠AOD,
所以∠EOF=∠AOE+∠AOF=(∠AOC+∠AOD)=90°,
所以∠COF=∠EOC+∠EOF=90°+α.
25. (1) 6 2
(2) ①16-2x
②因为CF=CE-EF=CE-AF=8-x,
所以BE=2CF.
(3) 因为点C运动到数轴上表示数-14的位置,CE=8,
所以点E表示的数为-6.
当点P向数轴正方向运动,且与点Q没有相遇时,
由题意,得3t+1=2t+2,解得t=1;
当点P向数轴正方向运动,且与点Q相遇后时,
由题意,得3t-1=2t+2,解得t=3;
当点P向数轴负方向运动,且与点Q没有相遇时,
由题意,得2(t-6)+1+2t=16,解得t=;
当点P向数轴负方向运动,且与点Q相遇后时,
由题意,得2(t-6)+2t=16+1,解得t=.
综上,当t的值为1或3或或时,P,Q两点间的距离为1个单位长度.
同课章节目录
