人教版九年级上册第二十二章 二次函数 单元试卷(含答案)
文档属性
| 名称 | 人教版九年级上册第二十二章 二次函数 单元试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 516.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 20:52:41 | ||
图片预览




文档简介
第二十二章 二次函数 单元试卷
一、选择题
1.下列函数解析式中,一定为二次函数的是( )
A. B. C. D.
2.抛物线 的对称轴是( )
A.直线 B.直线 C.直线 D.直线
3.将拋物线 向上平移 3 个单位后得到的拋物线的函数表达式是( )
A. B. C. D.
4.一个矩形周长为,不能围成的面积是( )
A. B. C. D.
5.已知二次函数y=ax2+bx+c中自变量x和函数y的部分对应值如下表:
x … -3 -2 -1 0 1 …
y … -1 -4 -1 8 23 …
则方程 ax2+bx+c=0的一个解x=t的取值范围下列可能的是( )
A.-36.若函数y=-2x2+bx+c的图象经过点(-1,1)和(1,-7),则当-3≤x≤0时,函数的最大值与最小值之和是( )
A.-8 B.-6 C.-3 D.0
7.在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
A. B.
C. D.
8.某抛物线型拱桥的示意图如图所示,水面,拱桥最高处点C到水面的距离为,在该抛物线上的点E,F处要安装两盏警示灯(点E,F关于y轴对称),警示灯F距水面的高度是,则这两盏灯的水平距离是( )
A. B. C. D.
9.二次函数的图象如图所示,则下列各式正确的是( )
A. B. C. D.
10.已知二次函数 及一次函数y=-x+m.将该二次函数在x 轴上方的图象沿x轴翻折到x 轴下方,图象的其余部分不变,得到一个新图象(如图所示).当直线 y=-x+m与新图象有4个交点时,m的取值范围是( ).
A. B.
C.-2二、填空题
11.若抛物线(是常数)与轴没有交点,则的取值范围是 .
12.拋物线 的开口向下,则 的值可以取 .(写出一个即可)
13.已知二次函数(,均是实数),设该函数最小值为,若,,则的取值范围是 .
14.抛物线的部分图像如图所示,则一元二次方程的根为 .
15.在中考体育测试中,小刚投出的实心球在空中的运动轨迹如图所示.实心球行进的高度与水平距离之间满足关系式,则实心球投出的水平距离为 .
16.建水双龙桥,俗称“十七孔桥”,位于云南省建水县,是一座具有极高历史,艺术和科学价值的古桥,如图,古桥横断面是抛物线形状,当水面在时,拱顶(拱桥洞的最高点)离水面,水面宽.则水面上升米后水面宽度为 米.
17.某宾馆有 120 间标准房,当标准房价格为 100 元时,每天都客满,市场调查表明单间房价在 元之间(含 100 元, 150 元)浮动时,每提高 10 元,日均入住数减少 6 间。如果不考虑其他因素,该宾馆将标准房价格提高到 元时,客房的日营业收入最大。
18.在“探索二次函数的系数a,b,c与图象的关系”活动中,老师给出了坐标系中的四个点:,,,.同学们分别画出了经过这四个点中的三个点的二次函数图象,并得到对应的函数表达式,则的最大值等于 .
三、解答题
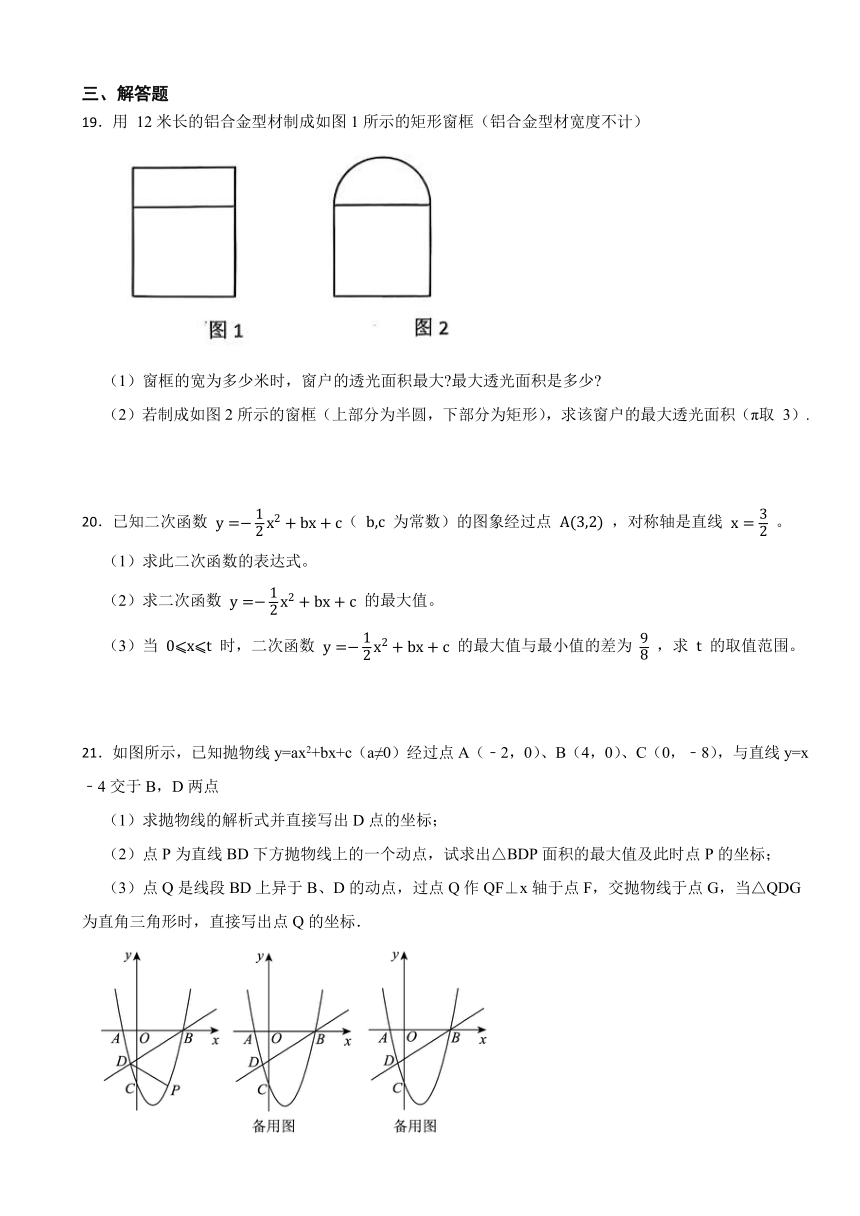
19.用 12米长的铝合金型材制成如图1所示的矩形窗框(铝合金型材宽度不计)
(1)窗框的宽为多少米时,窗户的透光面积最大 最大透光面积是多少
(2)若制成如图2所示的窗框(上部分为半圆,下部分为矩形),求该窗户的最大透光面积(π取 3).
20.已知二次函数 ( 为常数)的图象经过点 ,对称轴是直线 。
(1)求此二次函数的表达式。
(2)求二次函数 的最大值。
(3)当 时,二次函数 的最大值与最小值的差为 ,求 的取值范围。
21.如图所示,已知抛物线y=ax2+bx+c(a≠0)经过点A(﹣2,0)、B(4,0)、C(0,﹣8),与直线y=x﹣4交于B,D两点
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为直线BD下方抛物线上的一个动点,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G,当△QDG为直角三角形时,直接写出点Q的坐标.
22.今年“双”网上购物节,某童装专卖店在销售中发现,一款童装每件进价为元,销售价为元时,每天可售出件,商店决定采取适当的降价措施,以扩大销售量,尽快减少库存,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件,设每件童装降价元.
(1)每天可销售__________件,每件盈利__________元;(用含的代数式表示)
(2)若每天销售利润为元,当降价多少元时,每天的利润最大?
23.2024年巴黎奥运会女子单人10米跳台决赛中,全红婵以425.60分的总分夺得金牌.在精彩的比赛过程中,全红婵选择了一个极具难度的动作(如图1),为了分析这个动作我们可以建立如图2所示的平面直角坐标系,将她从点起跳后的运动路线看作抛物线的一部分,从起跳到入水的过程中,她的竖直高度(单位:)与水平距离(单位:)近似满足二次函数关系.
(1)下表为平时训练中完成一次动作,全红婵的水平距离与竖直高度的几组数据:
水平距离 3 4 4.5
竖直高度 10 11.25 10 6.25
根据表中数据,求与近似满足的二次函数解析式,并求出的值;
(2)某一次10米跳台练习中,如果与之间近似满足二次函数,则全红婵完成跳水动作入水时的入水点到点的距离是多少?
答案解析部分
1.【答案】B
2.【答案】A
【解析】【解答】解:抛物线y=(x-1)2的对称轴为直线x=1.
故答案选:A.
【分析】根据二次函数的顶点式方程y=(x -k)2+h的对称轴为x=k,顶点坐标为(k,h).
3.【答案】B
【解析】【解答】解:将抛物线y=x2向上平移3个单位后得到的抛物线的函数表达式是y=x2+3.
故答案为:B.
【分析】根据二次函数图象的平移变换规律,上加下减,左加右减,即可得出平移后的函数表达式.
4.【答案】D
5.【答案】C
【解析】【解答】解:由所给表格可知,当 时, y取值为负, 当 时, y取值为正,
所以 的一个解的取值范围为:
故答案为:C.
【分析】根据所给表格,得出当 时, y取值为负, 当 时,y取值为正,据此可得出方程 的一个解的取值范围.
6.【答案】B
【解析】【解答】解:由题意,∵函数 的图象经过点
和
∴函数为
∴当 时, 当 时,y最大值为1;当 时,y取最小值为
∴函数的最大值与最小值之和是:
故答案为:B.
【分析】依据题意,代入 和 求出b,c的值,即可得到函数解析式,再由二次函数的性质,结合 进而可以判断得解.
7.【答案】C
【解析】【解答】解:A、由直线经过一、二、三象限可得:a>0;
由抛物线的顶点在y轴的负半轴可得a<0;
∴矛盾,
∴此选项不符合题意;
B、由直线经过一、二、三象限可得:a>0;
由抛物线的开口向下可得,抛物线的二次项系数<0,
而抛物线的二次项系数为1>0,
∴矛盾,
∴此选项不符合题意;
C、由直线经过一、二、四象限可得:a<0;
由抛物线的顶点在y轴的负半轴可得a<0;
∴此选项符合题意;
D、由直线经过二、三、四象限可得:a<0,b<0,
而一次函数的解析式中b=2>0;
∴矛盾,
∴此选项不符合题意.
故答案为:C.
【分析】根据二次函数及一次函数的图象及性质可得,当a<0时,二次函数图象开口向上,顶点在y轴负半轴,一次函数经过一、二、四象限;当a>0时,二次函数图象开口向上,顶点在y轴正半轴,一次函数经过一、二、三象限;再结合各选项即可判断求解.
8.【答案】A
9.【答案】C
10.【答案】D
【解析】【解答】解:当y=0时,-x2+x+6=0,
解之:x1=3,x2=-2,
∴抛物线与x轴的交点坐标为(3,0),(-2,0)
当直线过点(-2,0)时,直线与新图象有3个交点,
∴2+m=0
解之:m=-2;
当直线与翻折到x轴下方的部分相切时,直线与新图象有3个交点,
∴即x2-6-m=0
∴△=0-4(-6-m)=0
解之:m=-6,
∵ 得到一个新图象(如图所示),直线 y=-x+m与新图象有4个交点,
∴ -6故答案为:D
【分析】由y=0可得到关于x的方程,解方程求出x的值,可得到抛物线与x轴的两个交点坐标,当直线过点(-2,0)时,直线与新图象有3个交点,可得到m的值,当直线与翻折到x轴下方的部分相切时,直线与新图象有3个交点,将两函数联立方程组,可得到关于x的方程有两个相等的实数根,可求出m的值;再根据直线 y=-x+m与新图象有4个交点,可得到m的取值范围.
11.【答案】
【解析】【解答】解:∵抛物线与x轴没有交点,
∴没有实数根,
∴,.
故答案为:.
【分析】
抛物线与x轴无交点,则关于x的一元二次方程无实数根,即.
12.【答案】-1
【解析】【解答】解:∵抛物线 的开口向下,
∴a的值可以为 .
故答案为:
【分析】二次函数的开口方向由二次项系数a决定, 当时, 开口向上, 当 时,开口向下.
13.【答案】
14.【答案】,
15.【答案】8
16.【答案】
17.【答案】150
【解析】【解答】解:设宾馆客房租金每间日租金提高x个10元,
将有6x间客房空出,客房租金总收入为y,
由题意可得:
y=(100+10x)(120-6x)(10≤x≤ 50且x是整数),
=60(-x2+10x+200)
=-60(x-5)2+13500
当x=5时,ymax=13500,
因此每间租金100+10×5=150元时,客房租金总收入最高,日租金13500元.
故答案为:150.
【分析】设标准房价格为x元,客房的日营业收入为y元,根据题意列出函数关系式,然后根据二次函数的性质即可求解.
18.【答案】2
【解析】【解答】解:∵A、B、C的纵坐标相同,
∴抛物线不会同时经过A、B、C三点,
∴抛物线可能经过A、D、C或者B、D、C或者A、B、D,
如图,经过A、D、C三点的抛物线,当时,y的值最大,
把代入,得,
解得,
∴经过A、D、C三点的抛物线的解析式为,
当时,,
故的最大值等于2,
故答案为:2.
【分析】由于A、B、C三点在同一条直线上,故抛物线不可能同时过这三点,因此抛物线可能经过A、D、C或者B、D、C或者A、B、D,画出图象后,则只有抛物线经过A、D、C三点且当时,y的值最大,然后用待定系数法求出函数解析式,再求出当时的函数值即可.
19.【答案】(1)设矩形窗框的宽AD为x米,窗户的透光面积为S平方米,如图所示:
则 (米) ,
根据题意得:
∴当 时, S最大, 最大值为6,∴窗框的宽为2米时,窗户的透光面积最大,最大透光面积是6平方米;
(2)解:设矩形窗框的宽AD为x米,窗户的透光面积为S平方米,如上图所示:
则半圆周长为 (米),
米,
∴当 时,S最大,最大值为
答:该窗户的最大透光面积为 平方米.
【解析】【分析】(1)设窗框的宽为. 则长为 (米),表示出面积利用二次函数最值求法得出即可;
(2)设矩形窗框的宽AD为x米,窗户的透光面积为S平方米,则半圆周长为 (米),
米,根据窗户的透光面积=半圆的面积+矩形的面积列出函数解析式,根据函数的性质求最值.
20.【答案】(1)解: 对称轴是直线 .
的图象经过点 .
(2)解: ,
其最大值为
(3)解: 的对称轴是直线 .
当 时,二次函数取得最大值 .
当 时,二次函数值为 2 .
而 当 时,恰好符合.
根据二次函数的对称性可得,
当 时,最大值仍然为函数本身的最大值,最小值为 时对应的函数值,亦符合.
故
【解析】【分析】(1)利用点A(3,2)和对称轴求出函数表达式;
(2)利用公式求出函数最大值;
(3)利用图象分析即可.
21.【答案】(1)y=(x+2)(x﹣4),D的坐标是(﹣1,﹣5);(2)P(,﹣);(3)点Q的坐标为(2,﹣2)或(3,﹣1).
22.【答案】(1),
(2)当降价为元时,每天的利润最大.
23.【答案】(1),
(2)
一、选择题
1.下列函数解析式中,一定为二次函数的是( )
A. B. C. D.
2.抛物线 的对称轴是( )
A.直线 B.直线 C.直线 D.直线
3.将拋物线 向上平移 3 个单位后得到的拋物线的函数表达式是( )
A. B. C. D.
4.一个矩形周长为,不能围成的面积是( )
A. B. C. D.
5.已知二次函数y=ax2+bx+c中自变量x和函数y的部分对应值如下表:
x … -3 -2 -1 0 1 …
y … -1 -4 -1 8 23 …
则方程 ax2+bx+c=0的一个解x=t的取值范围下列可能的是( )
A.-3
A.-8 B.-6 C.-3 D.0
7.在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
A. B.
C. D.
8.某抛物线型拱桥的示意图如图所示,水面,拱桥最高处点C到水面的距离为,在该抛物线上的点E,F处要安装两盏警示灯(点E,F关于y轴对称),警示灯F距水面的高度是,则这两盏灯的水平距离是( )
A. B. C. D.
9.二次函数的图象如图所示,则下列各式正确的是( )
A. B. C. D.
10.已知二次函数 及一次函数y=-x+m.将该二次函数在x 轴上方的图象沿x轴翻折到x 轴下方,图象的其余部分不变,得到一个新图象(如图所示).当直线 y=-x+m与新图象有4个交点时,m的取值范围是( ).
A. B.
C.-2
11.若抛物线(是常数)与轴没有交点,则的取值范围是 .
12.拋物线 的开口向下,则 的值可以取 .(写出一个即可)
13.已知二次函数(,均是实数),设该函数最小值为,若,,则的取值范围是 .
14.抛物线的部分图像如图所示,则一元二次方程的根为 .
15.在中考体育测试中,小刚投出的实心球在空中的运动轨迹如图所示.实心球行进的高度与水平距离之间满足关系式,则实心球投出的水平距离为 .
16.建水双龙桥,俗称“十七孔桥”,位于云南省建水县,是一座具有极高历史,艺术和科学价值的古桥,如图,古桥横断面是抛物线形状,当水面在时,拱顶(拱桥洞的最高点)离水面,水面宽.则水面上升米后水面宽度为 米.
17.某宾馆有 120 间标准房,当标准房价格为 100 元时,每天都客满,市场调查表明单间房价在 元之间(含 100 元, 150 元)浮动时,每提高 10 元,日均入住数减少 6 间。如果不考虑其他因素,该宾馆将标准房价格提高到 元时,客房的日营业收入最大。
18.在“探索二次函数的系数a,b,c与图象的关系”活动中,老师给出了坐标系中的四个点:,,,.同学们分别画出了经过这四个点中的三个点的二次函数图象,并得到对应的函数表达式,则的最大值等于 .
三、解答题
19.用 12米长的铝合金型材制成如图1所示的矩形窗框(铝合金型材宽度不计)
(1)窗框的宽为多少米时,窗户的透光面积最大 最大透光面积是多少
(2)若制成如图2所示的窗框(上部分为半圆,下部分为矩形),求该窗户的最大透光面积(π取 3).
20.已知二次函数 ( 为常数)的图象经过点 ,对称轴是直线 。
(1)求此二次函数的表达式。
(2)求二次函数 的最大值。
(3)当 时,二次函数 的最大值与最小值的差为 ,求 的取值范围。
21.如图所示,已知抛物线y=ax2+bx+c(a≠0)经过点A(﹣2,0)、B(4,0)、C(0,﹣8),与直线y=x﹣4交于B,D两点
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为直线BD下方抛物线上的一个动点,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G,当△QDG为直角三角形时,直接写出点Q的坐标.
22.今年“双”网上购物节,某童装专卖店在销售中发现,一款童装每件进价为元,销售价为元时,每天可售出件,商店决定采取适当的降价措施,以扩大销售量,尽快减少库存,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件,设每件童装降价元.
(1)每天可销售__________件,每件盈利__________元;(用含的代数式表示)
(2)若每天销售利润为元,当降价多少元时,每天的利润最大?
23.2024年巴黎奥运会女子单人10米跳台决赛中,全红婵以425.60分的总分夺得金牌.在精彩的比赛过程中,全红婵选择了一个极具难度的动作(如图1),为了分析这个动作我们可以建立如图2所示的平面直角坐标系,将她从点起跳后的运动路线看作抛物线的一部分,从起跳到入水的过程中,她的竖直高度(单位:)与水平距离(单位:)近似满足二次函数关系.
(1)下表为平时训练中完成一次动作,全红婵的水平距离与竖直高度的几组数据:
水平距离 3 4 4.5
竖直高度 10 11.25 10 6.25
根据表中数据,求与近似满足的二次函数解析式,并求出的值;
(2)某一次10米跳台练习中,如果与之间近似满足二次函数,则全红婵完成跳水动作入水时的入水点到点的距离是多少?
答案解析部分
1.【答案】B
2.【答案】A
【解析】【解答】解:抛物线y=(x-1)2的对称轴为直线x=1.
故答案选:A.
【分析】根据二次函数的顶点式方程y=(x -k)2+h的对称轴为x=k,顶点坐标为(k,h).
3.【答案】B
【解析】【解答】解:将抛物线y=x2向上平移3个单位后得到的抛物线的函数表达式是y=x2+3.
故答案为:B.
【分析】根据二次函数图象的平移变换规律,上加下减,左加右减,即可得出平移后的函数表达式.
4.【答案】D
5.【答案】C
【解析】【解答】解:由所给表格可知,当 时, y取值为负, 当 时, y取值为正,
所以 的一个解的取值范围为:
故答案为:C.
【分析】根据所给表格,得出当 时, y取值为负, 当 时,y取值为正,据此可得出方程 的一个解的取值范围.
6.【答案】B
【解析】【解答】解:由题意,∵函数 的图象经过点
和
∴函数为
∴当 时, 当 时,y最大值为1;当 时,y取最小值为
∴函数的最大值与最小值之和是:
故答案为:B.
【分析】依据题意,代入 和 求出b,c的值,即可得到函数解析式,再由二次函数的性质,结合 进而可以判断得解.
7.【答案】C
【解析】【解答】解:A、由直线经过一、二、三象限可得:a>0;
由抛物线的顶点在y轴的负半轴可得a<0;
∴矛盾,
∴此选项不符合题意;
B、由直线经过一、二、三象限可得:a>0;
由抛物线的开口向下可得,抛物线的二次项系数<0,
而抛物线的二次项系数为1>0,
∴矛盾,
∴此选项不符合题意;
C、由直线经过一、二、四象限可得:a<0;
由抛物线的顶点在y轴的负半轴可得a<0;
∴此选项符合题意;
D、由直线经过二、三、四象限可得:a<0,b<0,
而一次函数的解析式中b=2>0;
∴矛盾,
∴此选项不符合题意.
故答案为:C.
【分析】根据二次函数及一次函数的图象及性质可得,当a<0时,二次函数图象开口向上,顶点在y轴负半轴,一次函数经过一、二、四象限;当a>0时,二次函数图象开口向上,顶点在y轴正半轴,一次函数经过一、二、三象限;再结合各选项即可判断求解.
8.【答案】A
9.【答案】C
10.【答案】D
【解析】【解答】解:当y=0时,-x2+x+6=0,
解之:x1=3,x2=-2,
∴抛物线与x轴的交点坐标为(3,0),(-2,0)
当直线过点(-2,0)时,直线与新图象有3个交点,
∴2+m=0
解之:m=-2;
当直线与翻折到x轴下方的部分相切时,直线与新图象有3个交点,
∴即x2-6-m=0
∴△=0-4(-6-m)=0
解之:m=-6,
∵ 得到一个新图象(如图所示),直线 y=-x+m与新图象有4个交点,
∴ -6
【分析】由y=0可得到关于x的方程,解方程求出x的值,可得到抛物线与x轴的两个交点坐标,当直线过点(-2,0)时,直线与新图象有3个交点,可得到m的值,当直线与翻折到x轴下方的部分相切时,直线与新图象有3个交点,将两函数联立方程组,可得到关于x的方程有两个相等的实数根,可求出m的值;再根据直线 y=-x+m与新图象有4个交点,可得到m的取值范围.
11.【答案】
【解析】【解答】解:∵抛物线与x轴没有交点,
∴没有实数根,
∴,.
故答案为:.
【分析】
抛物线与x轴无交点,则关于x的一元二次方程无实数根,即.
12.【答案】-1
【解析】【解答】解:∵抛物线 的开口向下,
∴a的值可以为 .
故答案为:
【分析】二次函数的开口方向由二次项系数a决定, 当时, 开口向上, 当 时,开口向下.
13.【答案】
14.【答案】,
15.【答案】8
16.【答案】
17.【答案】150
【解析】【解答】解:设宾馆客房租金每间日租金提高x个10元,
将有6x间客房空出,客房租金总收入为y,
由题意可得:
y=(100+10x)(120-6x)(10≤x≤ 50且x是整数),
=60(-x2+10x+200)
=-60(x-5)2+13500
当x=5时,ymax=13500,
因此每间租金100+10×5=150元时,客房租金总收入最高,日租金13500元.
故答案为:150.
【分析】设标准房价格为x元,客房的日营业收入为y元,根据题意列出函数关系式,然后根据二次函数的性质即可求解.
18.【答案】2
【解析】【解答】解:∵A、B、C的纵坐标相同,
∴抛物线不会同时经过A、B、C三点,
∴抛物线可能经过A、D、C或者B、D、C或者A、B、D,
如图,经过A、D、C三点的抛物线,当时,y的值最大,
把代入,得,
解得,
∴经过A、D、C三点的抛物线的解析式为,
当时,,
故的最大值等于2,
故答案为:2.
【分析】由于A、B、C三点在同一条直线上,故抛物线不可能同时过这三点,因此抛物线可能经过A、D、C或者B、D、C或者A、B、D,画出图象后,则只有抛物线经过A、D、C三点且当时,y的值最大,然后用待定系数法求出函数解析式,再求出当时的函数值即可.
19.【答案】(1)设矩形窗框的宽AD为x米,窗户的透光面积为S平方米,如图所示:
则 (米) ,
根据题意得:
∴当 时, S最大, 最大值为6,∴窗框的宽为2米时,窗户的透光面积最大,最大透光面积是6平方米;
(2)解:设矩形窗框的宽AD为x米,窗户的透光面积为S平方米,如上图所示:
则半圆周长为 (米),
米,
∴当 时,S最大,最大值为
答:该窗户的最大透光面积为 平方米.
【解析】【分析】(1)设窗框的宽为. 则长为 (米),表示出面积利用二次函数最值求法得出即可;
(2)设矩形窗框的宽AD为x米,窗户的透光面积为S平方米,则半圆周长为 (米),
米,根据窗户的透光面积=半圆的面积+矩形的面积列出函数解析式,根据函数的性质求最值.
20.【答案】(1)解: 对称轴是直线 .
的图象经过点 .
(2)解: ,
其最大值为
(3)解: 的对称轴是直线 .
当 时,二次函数取得最大值 .
当 时,二次函数值为 2 .
而 当 时,恰好符合.
根据二次函数的对称性可得,
当 时,最大值仍然为函数本身的最大值,最小值为 时对应的函数值,亦符合.
故
【解析】【分析】(1)利用点A(3,2)和对称轴求出函数表达式;
(2)利用公式求出函数最大值;
(3)利用图象分析即可.
21.【答案】(1)y=(x+2)(x﹣4),D的坐标是(﹣1,﹣5);(2)P(,﹣);(3)点Q的坐标为(2,﹣2)或(3,﹣1).
22.【答案】(1),
(2)当降价为元时,每天的利润最大.
23.【答案】(1),
(2)
同课章节目录
