2025年辽宁省抚顺市新宾县木奇镇中学中考数学模拟试卷(一)(含部分答案)
文档属性
| 名称 | 2025年辽宁省抚顺市新宾县木奇镇中学中考数学模拟试卷(一)(含部分答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 231.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 00:00:00 | ||
图片预览




文档简介
2025年辽宁省抚顺市新宾县木奇镇中学中考数学模拟试卷(一)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.南湖公园是长春市著名旅游景点之一,图①是公园中“四角亭”景观的照片,图②是其航拍照片,则图③是“四角亭”景观的( )
A. 主视图 B. 俯视图 C. 左视图 D. 右视图
2.四个城市某天中午12时的气温如表所示,其中气温最低的城市是( )
城市 鞍山 沈阳 抚顺 大连
气温/℃ 0 -1 -2 3
A. 沈阳 B. 大连 C. 鞍山 D. 抚顺
3.2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为( )
A. 3.84×104 B. 3.84×105 C. 3.84×106 D. 38.4×105
4.如图,AB∥CD,若∠1=65°,∠2=120°,则∠3的度数为( )
A. 45
B. 55°
C. 60°
D. 65°
5.下列运算正确的是( )
A. a7-a3=a4 B. 3a2 2a2=6a2 C. (-2a)3=-8a3 D. a4÷a4=a
6.七巧板、九连环、华容道、鲁班锁是深受大家喜爱的益智玩具.现将1个七巧板,2个九连环,1个华容道,2个鲁班锁分别装在6个不透明的盒子中(每个盒子装1个),所有盒子除里面的玩具外均相同.从这6个盒子中随机抽取1个盒子,抽中七巧板的概率是( )
A. B. C. D.
7.端午节是中国传统节日,下列与端午节有关的文创图案中,是轴对称图形的是( )
A. B.
C. D.
8.《九章算术》中记载这样一个题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,问牛和羊各值多少金?设每头牛值x金,每只羊值y金,可列方程为( )
A. B. C. D.
9.如图,在平面直角坐标系中,正方形OABC的顶点A在x轴上,顶点C在y轴上,顶点B的坐标为(6,6).若直线l经过点(-1,0),且将正方形OABC分割成面积相等的两部分,则直线l的函数解析式是( )
A. y=x-1
B.
C.
D.
10.如图,四边形ABCD为平行四边形,AB=4,BC=5,对角线BD=3,P为AD上的一个动点,Q为AB上的一个定点,则的最小值为( )
A. 4 B. 3 C. 6 D. 5
二、填空题:本题共5小题,每小题3分,共15分。
11.分式方程的解是______.
12.如图,在等腰三角形ABC中,AB=AC=2,∠BAC=120°,将△ABC沿其底边中线向下平移,使点A的对应点满足,则平移前后的两个三角形重叠部分的面积是______.
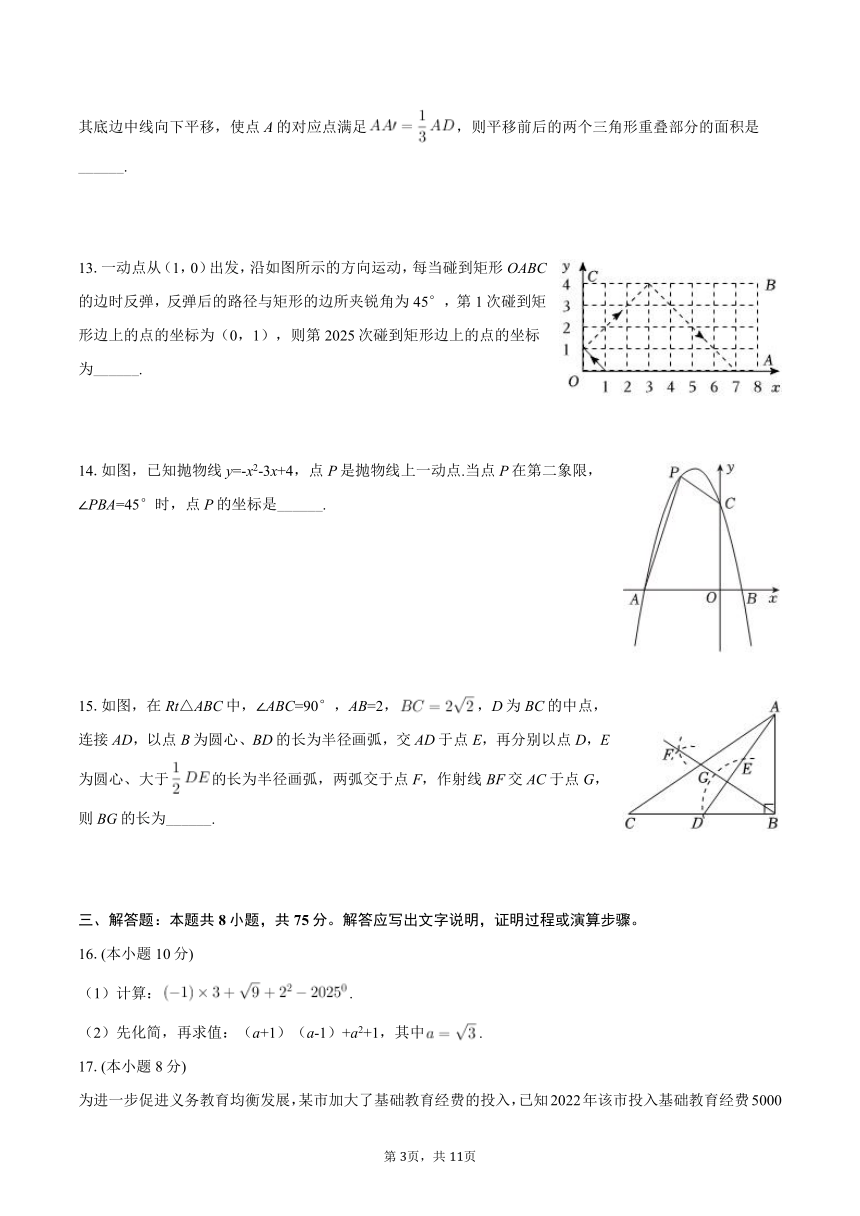
13.一动点从(1,0)出发,沿如图所示的方向运动,每当碰到矩形OABC的边时反弹,反弹后的路径与矩形的边所夹锐角为45°,第1次碰到矩形边上的点的坐标为(0,1),则第2025次碰到矩形边上的点的坐标为______.
14.如图,已知抛物线y=-x2-3x+4,点P是抛物线上一动点.当点P在第二象限,∠PBA=45°时,点P的坐标是______.
15.如图,在Rt△ABC中,∠ABC=90°,AB=2,,D为BC的中点,连接AD,以点B为圆心、BD的长为半径画弧,交AD于点E,再分别以点D,E为圆心、大于的长为半径画弧,两弧交于点F,作射线BF交AC于点G,则BG的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
(1)计算:.
(2)先化简,再求值:(a+1)(a-1)+a2+1,其中.
17.(本小题8分)
为进一步促进义务教育均衡发展,某市加大了基础教育经费的投入,已知2022年该市投入基础教育经费5000万元,2024年投入基础教育经费7200万元.
(1)求该市这两年投入基础教育经费的年平均增长率.
(2)如果按(1)中基础教育经费投入的年平均增长率计算,该市计划2025年用不超过当年基础教育经费的5%购买电脑和实物投影仪共2000台,调配给农村学校.若购买一台电脑需3000元,购买一台实物投影仪需1500元,则最多可购买电脑多少台?
18.(本小题8分)
水资源问题是全球关注的热点,节约用水已成为全民共识.某校课外兴趣小组想了解居民家庭用水情况,他们从一小区随机抽取了30户家庭,收集了这30户家庭去年7月份的用水量,并对这30个数据进行整理,绘制了如下统计图表:
组别 用水量x/m3 组内平均数/m3
A 2≤x<6 5.3
B 6≤x<10 8.0
C 10≤x<14 12.5
D 14≤x<18 15.5
根据以上信息,解答下列问题:
(1)这30个数据的中位数落在______组(填组别);
(2)求这30户家庭去年7月份的总用水量;
(3)该小区有1000户家庭,若每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约10%,请估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约多少m3?
19.(本小题8分)
伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销售量y(吨)与每吨的销售价x(万元)之间的函数关系如图所示.
(1)求出y与x之间的函数关系式.
(2)如果销售利润为W万元,当每吨的销售价定为多少万元时,销售利润最大?最大利润是多少?
20.(本小题8分)
中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,∠ABQ=60°,AB=5.4m,CE=1.6m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1m,参考数据≈1.73)
(1)求PQ的长;
(2)该充电站有20个停车位,求PN的长.
21.(本小题8分)
如图,已知AB是⊙O的直径,点C,D在⊙O上,且BC=CD.点E是线段AB延长线上一点,连接EC并延长交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°.
(1)求证:EF是⊙O的切线;
(2)若BE=2,CE=4,求AF的长.
22.(本小题12分)
如图1,一副三角板分别记作△ABC和△DEF,其中∠ABC=∠DEF=90°,∠BAC=45°,∠EDF=30°,AC=DF=4,作∠ABC的平分线BQ交AC于点M.
(1)求证:BM=EF.
(2)在同一平面内,将图1中的两个三角形按如图2所示的方式放置,点A与点D重合,点E落在AC上.将图2中的△AEF绕点A按逆时针方向旋转,连接CE.
①如图3,在旋转△AEF的过程中,当点F落在角平分线BQ上时,求CE的长;
②如图4,在旋转△AEF的过程中,当AF∥BQ时,连接BF,CF,求△BCF的面积.
(3)在(2)的条件下,连接CF.如图5,在△AEF旋转的过程中,当CE落在△ABC的边BC所在的直线上时,求△CEF的面积.
23.(本小题13分)
如图,已知抛物线y=-x2+2x+1与y轴交于点A(0,1).过点A作直线AB∥x轴,交抛物线于另一点B,此时,我们将这条直线AB命名为抛物线y=-x2+2x+1的“最美分割线”,于是我们定义:在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴的交点坐标为(0,c),那么我们把经过点(0,c)且平行于x轴的直线称为这条抛物线的“最美分割线”.
(1)求抛物线y=x2-2x+3的“最美分割线”与这条抛物线的交点坐标.
(2)经过点A(-4,0)和B(x,0)(x>-4)的抛物线与y轴交于点C,它的“最美分割线”与该抛物线的另一个交点为D,请用含m的代数式表示点D的坐标.
(3)在(2)的条件下,设抛物线的顶点为P,直线EF垂直平分OC,垂足为E,交该抛物线的对称轴于点F.
①连接CF,DF,当∠DFC=90°时,求点P的坐标.
②若直线EF与直线MN关于“最美分割线”对称,是否存在使点P到直线MN的距离与点B到直线EF的距离之比为3:2的m的值?若存在,请直接写出m的值;若不存在,请说明理由.
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】x=3
12.【答案】
13.【答案】(7,0)
14.【答案】(-3,4)
15.【答案】
16.【答案】3;
2 a2,6.
17.【答案】20%;
880台.
18.【答案】解:(1)B;
(2)这30户家庭去年7月份的总用水量为5.3×10+8.0×12+12.5×6+15.5×2=255(m3);
(3)这30户家庭去年7月份的平均用水量为255÷30=8.5(m3),
∵每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约10%,
∴今年每户家庭7月份节约的用水量为8.5×10%=0.85(m3),
∴估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约0.85×1000=850(m3).
19.【答案】y与x之间的函数关系式为y=-x+2.6;
当每吨的销售价定为1.5万元时,销售利润最大,最大利润是1.21万元.
20.【答案】解:(1)∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
在Rt△ABQ中,∠ABQ=60°,AB=5.4m,
∴AQ=AB sin,∠QAB=30°,
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°,
∴∠CBE=30°,
∴,
∴,
∵∠PAD=180°-30°-90°=60°,
∴,
∴;
(2)在Rt△BCE中,,
在Rt△ABQ中,BQ=AB cos∠ABQ=2.7m,
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7m,
∵四边形ABCD是矩形,
∴PN=QM=66.7m.
21.【答案】(1)证明:如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵BC=CD,
∴∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AF,
∵EH平分∠FEG,
∴∠FEH=∠GEH,
∵∠GEH=∠H+∠BAC,∠FEH=∠F+∠BAF,
∴2∠H+2∠BAC=∠F+∠BAF,
∴∠BAF=2∠BAC,
∴∠F=2∠H=90°,
∴∠OCE=∠F=90°,
即OC⊥EF,
∵OC是半径,
∴EF是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,即∠OCB+∠BCE=90°,
∴∠OBC+∠BAC=90°,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠BCE=∠EAC,
∵∠CEB=∠CAE,
∴△BCE∽△CAE,
∴====,
∴CE2=BE AE,即16=2AE,
解得AE=8,
∴AB=8-2=6,
在Rt△ABC中,AB=6,=,
∴BC=,AC=,
∵∠F=∠ACB=90°,∠FAC=∠BAC,
∴△FAC∽△CAB,
∴=,
∴AF==.
22.【答案】见解析;
②2;
②8;
或.
23.【答案】“最美分制线”与这条抛物线的交点坐标为(0.3)和(2,3);
点D的坐标为(2m,4m+8);
①点P的坐标为;
②存在,m的值为或.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.南湖公园是长春市著名旅游景点之一,图①是公园中“四角亭”景观的照片,图②是其航拍照片,则图③是“四角亭”景观的( )
A. 主视图 B. 俯视图 C. 左视图 D. 右视图
2.四个城市某天中午12时的气温如表所示,其中气温最低的城市是( )
城市 鞍山 沈阳 抚顺 大连
气温/℃ 0 -1 -2 3
A. 沈阳 B. 大连 C. 鞍山 D. 抚顺
3.2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为( )
A. 3.84×104 B. 3.84×105 C. 3.84×106 D. 38.4×105
4.如图,AB∥CD,若∠1=65°,∠2=120°,则∠3的度数为( )
A. 45
B. 55°
C. 60°
D. 65°
5.下列运算正确的是( )
A. a7-a3=a4 B. 3a2 2a2=6a2 C. (-2a)3=-8a3 D. a4÷a4=a
6.七巧板、九连环、华容道、鲁班锁是深受大家喜爱的益智玩具.现将1个七巧板,2个九连环,1个华容道,2个鲁班锁分别装在6个不透明的盒子中(每个盒子装1个),所有盒子除里面的玩具外均相同.从这6个盒子中随机抽取1个盒子,抽中七巧板的概率是( )
A. B. C. D.
7.端午节是中国传统节日,下列与端午节有关的文创图案中,是轴对称图形的是( )
A. B.
C. D.
8.《九章算术》中记载这样一个题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,问牛和羊各值多少金?设每头牛值x金,每只羊值y金,可列方程为( )
A. B. C. D.
9.如图,在平面直角坐标系中,正方形OABC的顶点A在x轴上,顶点C在y轴上,顶点B的坐标为(6,6).若直线l经过点(-1,0),且将正方形OABC分割成面积相等的两部分,则直线l的函数解析式是( )
A. y=x-1
B.
C.
D.
10.如图,四边形ABCD为平行四边形,AB=4,BC=5,对角线BD=3,P为AD上的一个动点,Q为AB上的一个定点,则的最小值为( )
A. 4 B. 3 C. 6 D. 5
二、填空题:本题共5小题,每小题3分,共15分。
11.分式方程的解是______.
12.如图,在等腰三角形ABC中,AB=AC=2,∠BAC=120°,将△ABC沿其底边中线向下平移,使点A的对应点满足,则平移前后的两个三角形重叠部分的面积是______.
13.一动点从(1,0)出发,沿如图所示的方向运动,每当碰到矩形OABC的边时反弹,反弹后的路径与矩形的边所夹锐角为45°,第1次碰到矩形边上的点的坐标为(0,1),则第2025次碰到矩形边上的点的坐标为______.
14.如图,已知抛物线y=-x2-3x+4,点P是抛物线上一动点.当点P在第二象限,∠PBA=45°时,点P的坐标是______.
15.如图,在Rt△ABC中,∠ABC=90°,AB=2,,D为BC的中点,连接AD,以点B为圆心、BD的长为半径画弧,交AD于点E,再分别以点D,E为圆心、大于的长为半径画弧,两弧交于点F,作射线BF交AC于点G,则BG的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
(1)计算:.
(2)先化简,再求值:(a+1)(a-1)+a2+1,其中.
17.(本小题8分)
为进一步促进义务教育均衡发展,某市加大了基础教育经费的投入,已知2022年该市投入基础教育经费5000万元,2024年投入基础教育经费7200万元.
(1)求该市这两年投入基础教育经费的年平均增长率.
(2)如果按(1)中基础教育经费投入的年平均增长率计算,该市计划2025年用不超过当年基础教育经费的5%购买电脑和实物投影仪共2000台,调配给农村学校.若购买一台电脑需3000元,购买一台实物投影仪需1500元,则最多可购买电脑多少台?
18.(本小题8分)
水资源问题是全球关注的热点,节约用水已成为全民共识.某校课外兴趣小组想了解居民家庭用水情况,他们从一小区随机抽取了30户家庭,收集了这30户家庭去年7月份的用水量,并对这30个数据进行整理,绘制了如下统计图表:
组别 用水量x/m3 组内平均数/m3
A 2≤x<6 5.3
B 6≤x<10 8.0
C 10≤x<14 12.5
D 14≤x<18 15.5
根据以上信息,解答下列问题:
(1)这30个数据的中位数落在______组(填组别);
(2)求这30户家庭去年7月份的总用水量;
(3)该小区有1000户家庭,若每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约10%,请估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约多少m3?
19.(本小题8分)
伴随经济发展和生活水平的日益提高,水果超市如雨后春笋般兴起.万松园一水果超市从外地购进一批水果,其进货成本是每吨0.4万元,根据预测,此批水果一段时间内的销售量y(吨)与每吨的销售价x(万元)之间的函数关系如图所示.
(1)求出y与x之间的函数关系式.
(2)如果销售利润为W万元,当每吨的销售价定为多少万元时,销售利润最大?最大利润是多少?
20.(本小题8分)
中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,∠ABQ=60°,AB=5.4m,CE=1.6m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1m,参考数据≈1.73)
(1)求PQ的长;
(2)该充电站有20个停车位,求PN的长.
21.(本小题8分)
如图,已知AB是⊙O的直径,点C,D在⊙O上,且BC=CD.点E是线段AB延长线上一点,连接EC并延长交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°.
(1)求证:EF是⊙O的切线;
(2)若BE=2,CE=4,求AF的长.
22.(本小题12分)
如图1,一副三角板分别记作△ABC和△DEF,其中∠ABC=∠DEF=90°,∠BAC=45°,∠EDF=30°,AC=DF=4,作∠ABC的平分线BQ交AC于点M.
(1)求证:BM=EF.
(2)在同一平面内,将图1中的两个三角形按如图2所示的方式放置,点A与点D重合,点E落在AC上.将图2中的△AEF绕点A按逆时针方向旋转,连接CE.
①如图3,在旋转△AEF的过程中,当点F落在角平分线BQ上时,求CE的长;
②如图4,在旋转△AEF的过程中,当AF∥BQ时,连接BF,CF,求△BCF的面积.
(3)在(2)的条件下,连接CF.如图5,在△AEF旋转的过程中,当CE落在△ABC的边BC所在的直线上时,求△CEF的面积.
23.(本小题13分)
如图,已知抛物线y=-x2+2x+1与y轴交于点A(0,1).过点A作直线AB∥x轴,交抛物线于另一点B,此时,我们将这条直线AB命名为抛物线y=-x2+2x+1的“最美分割线”,于是我们定义:在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴的交点坐标为(0,c),那么我们把经过点(0,c)且平行于x轴的直线称为这条抛物线的“最美分割线”.
(1)求抛物线y=x2-2x+3的“最美分割线”与这条抛物线的交点坐标.
(2)经过点A(-4,0)和B(x,0)(x>-4)的抛物线与y轴交于点C,它的“最美分割线”与该抛物线的另一个交点为D,请用含m的代数式表示点D的坐标.
(3)在(2)的条件下,设抛物线的顶点为P,直线EF垂直平分OC,垂足为E,交该抛物线的对称轴于点F.
①连接CF,DF,当∠DFC=90°时,求点P的坐标.
②若直线EF与直线MN关于“最美分割线”对称,是否存在使点P到直线MN的距离与点B到直线EF的距离之比为3:2的m的值?若存在,请直接写出m的值;若不存在,请说明理由.
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】x=3
12.【答案】
13.【答案】(7,0)
14.【答案】(-3,4)
15.【答案】
16.【答案】3;
2 a2,6.
17.【答案】20%;
880台.
18.【答案】解:(1)B;
(2)这30户家庭去年7月份的总用水量为5.3×10+8.0×12+12.5×6+15.5×2=255(m3);
(3)这30户家庭去年7月份的平均用水量为255÷30=8.5(m3),
∵每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约10%,
∴今年每户家庭7月份节约的用水量为8.5×10%=0.85(m3),
∴估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约0.85×1000=850(m3).
19.【答案】y与x之间的函数关系式为y=-x+2.6;
当每吨的销售价定为1.5万元时,销售利润最大,最大利润是1.21万元.
20.【答案】解:(1)∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
在Rt△ABQ中,∠ABQ=60°,AB=5.4m,
∴AQ=AB sin,∠QAB=30°,
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°,
∴∠CBE=30°,
∴,
∴,
∵∠PAD=180°-30°-90°=60°,
∴,
∴;
(2)在Rt△BCE中,,
在Rt△ABQ中,BQ=AB cos∠ABQ=2.7m,
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7m,
∵四边形ABCD是矩形,
∴PN=QM=66.7m.
21.【答案】(1)证明:如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵BC=CD,
∴∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AF,
∵EH平分∠FEG,
∴∠FEH=∠GEH,
∵∠GEH=∠H+∠BAC,∠FEH=∠F+∠BAF,
∴2∠H+2∠BAC=∠F+∠BAF,
∴∠BAF=2∠BAC,
∴∠F=2∠H=90°,
∴∠OCE=∠F=90°,
即OC⊥EF,
∵OC是半径,
∴EF是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,即∠OCB+∠BCE=90°,
∴∠OBC+∠BAC=90°,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠BCE=∠EAC,
∵∠CEB=∠CAE,
∴△BCE∽△CAE,
∴====,
∴CE2=BE AE,即16=2AE,
解得AE=8,
∴AB=8-2=6,
在Rt△ABC中,AB=6,=,
∴BC=,AC=,
∵∠F=∠ACB=90°,∠FAC=∠BAC,
∴△FAC∽△CAB,
∴=,
∴AF==.
22.【答案】见解析;
②2;
②8;
或.
23.【答案】“最美分制线”与这条抛物线的交点坐标为(0.3)和(2,3);
点D的坐标为(2m,4m+8);
①点P的坐标为;
②存在,m的值为或.
第1页,共1页
同课章节目录
