2024-2025学年黑龙江省绥化市兰西一中高二(下)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年黑龙江省绥化市兰西一中高二(下)期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 81.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 13:47:28 | ||
图片预览


文档简介
2024-2025学年黑龙江省绥化市兰西一中高二(下)期中数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某邮局有4个不同的信箱,现有5封不同的信需要邮寄,则不同的投递方法共有( )
A. 45种 B. 54种 C. C种 D. A种
2.有10台不同的电视机,其中甲型3台,乙型3台,丙型4台.现从中任意取出3台,若其中至少含有两种不同的型号,则不同的取法共有( )
A. 96种 B. 108种 C. 114种 D. 118种
3.在的二项展开式中,x的系数为( )
A. -10 B. 10 C. -40 D. 40
4.如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
A. 84 B. 72 C. 64 D. 56
5.在正项等比数列{an}中,a3a4a5=512,a7=64,若当x∈N*时,2an-8n-t≥0恒成立,则实数t的取值范围为( )
A. (-∞,16] B. (-∞,-16] C. (-∞,-20] D. (-∞,20]
6.若点P是曲线y=x2-lnx上任意一点,则点P到直线y=x-1的最小距离为( )
A. 0 B. C. D.
7.已知数列{an}满足a1=1,,,则数列{an}的前2025项的和( )
A. 31012-2025 B. 31012-2027 C. 31013-2025 D. 31013-2027
8.已知函数f(x)是定义在R上的奇函数,f(x)的图象连续,且f(1)=0,记f(x)的导函数为f′(x),若xlnx f′(x)+f(x)<0在(0,+∞)上恒成立,则使(x2-x-6)f(x)>0成立的x的取值范围是( )
A. (-2,-1)∪(-1,0)∪(0,1)∪(1,3)
B. (-∞,-2)∪(3,+∞)
C. (-2,-1)∪(-1,0)∪(3,+∞)
D. (-∞,-2)∪(0,1)∪(1,3)
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
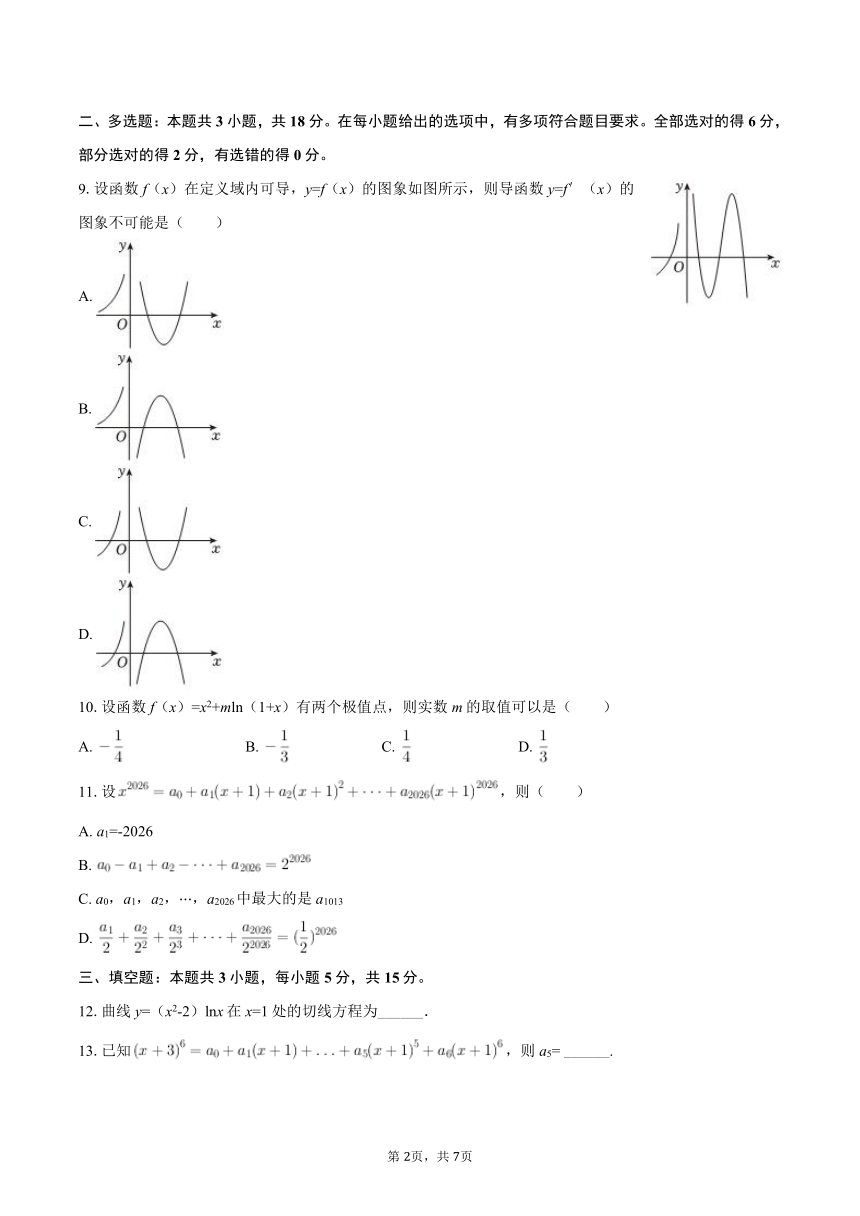
9.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象不可能是( )
A.
B.
C.
D.
10.设函数f(x)=x2+mln(1+x)有两个极值点,则实数m的取值可以是( )
A. B. C. D.
11.设,则( )
A. a1=-2026
B.
C. a0,a1,a2, ,a2026中最大的是a1013
D.
三、填空题:本题共3小题,每小题5分,共15分。
12.曲线y=(x2-2)lnx在x=1处的切线方程为______.
13.已知,则a5= ______.
14.已知函数在区间(2,3)上存在极小值点,则实数a的取值范围为______.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
有5名同学站成一排拍照.
(1)若甲乙必须站一起,则共有多少种不同的排法?
(2)若最左端只能排甲或乙,且最右端不能排甲,则共有多少种不同的排法?
(3)求出现甲必须站正中间,并且乙、丙两位同学不能相邻的排法?
16.(本小题12分)
的展开式一共有16项.
(1)求展开式中二项式系数之和;
(2)求展开式中的常数项.
17.(本小题12分)
已知函数f(x)=xlnx+2x-1.
(1)求f(x)的单调区间;
(2)若对任意的x>1,都有f(x)-k(x-1)>0(k∈Z)恒成立,求k的最大值.
18.(本小题12分)
已知正项数列{an}满足,a1=1.数列{bn}满足各项均不为0,b1=4,其前n项的乘积.
(1)求数列{an}通项公式;
(2)设cn=log2bn,求数列{cn}的通项公式;
(3)记数列{(-1)nan}的前2m项的和S2m,求使得不等式S2m≥c1+c2+ +c10成立的正整数m的最小值.
19.(本小题12分)
已知函数.
(1)求证:对于任意实数a,曲线y=f(x)在x=1处的切线恒过原点;
(2)讨论函数f(x)的零点个数.
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】ACD
10.【答案】CD
11.【答案】AB
12.【答案】x+y-1=0
13.【答案】12
14.【答案】
15.【答案】解:(1)根据题意,将甲乙看成一个元素,再与其他3人全排列即可,
有AA=48种排法;
(2)根据题意,分2种情况讨论:
①甲在最左端,有A=24种排法,
②乙在最左端,有CA=18种排法,
则共有24+18=42种排法;
(3)根据题意,甲师必须站正中间,有1种情况,
若乙、丙两位同学不能相邻,即乙丙在甲的两边,有2×2×2×2=16种排法;
故有1×16=16种排法.
16.【答案】215; 96096.
17.【答案】解:(1)已知f(x)=xlnx+2x-1,函数的定义域为(0,+∞),
可得f′(x)=lnx+3,
当0<x<e-3时,f′(x)<0,当x>e-3时,f′(x)>0,
则函数f(x)的单调减区间为(0,e-3),单调增区间为(e-3,+∞);
(2)若对任意的x>1,都有f(x)-k(x-1)>0(k∈Z)恒成立,
即在x>1上恒成立,
不妨设,
可得,
不妨设h(x)=x-2-lnx,函数定义域为(1,+∞),
可得,
所以函数h(x)在(1,+∞)上单调递增,
又h(3)=1-ln3<0,h(4)=2-ln4>0,
所以存在唯一的x0∈(3,4),使得h(x0)=0,
此时lnx0=x0-2,
当x∈(1,x0)时,h(x)<0,g′(x)<0,g(x)单调递减;
当x∈(x0,+∞)时,h(x)>0,g′(x)>0,g(x)单调递增,
所以,
则k<x0+1∈(4,5),
又k∈Z,
故实数k的最大值为4.
18.【答案】解:(1)依题意,当n≥2时,
由an-an-1=+,
可得(+)(-)=+,
∵an>0,n∈N*,
∴+>0,
∴,
∵=1,
∴数列是以1为首项为1,1为公差的等差数列,
∴,
∴,n∈N*.
(2)由题意,当n=1时,4=b1=T1=20b2,即b2=4,
当n≥2时,由①,
可得②,
,可得,
整理,得2bn+1=,
∵当n=1时,b1=4,b2=4,2b2≠不满足上式,
∴2bn+1=,(n∈N*,n≥2),
当n≥2时,对2bn+1=两边取以2为底的对数,
可得log22bn+1=log2,
化简,得log2bn+1+1=2log2bn,
即cn+1+1=2cn,
则cn+1=2cn-1,
两边同时减1,可得cn+1-1=2cn-1-1=2(cn-1),
∵c2-1=log2b2-1=1,
∴数列{cn-1}从第二项起是以1为首项,2为公比的等比数列,
∴,
∴,
∵c1=log2b1=2,
∴.
(3)∵,
∴,
而,
∴2log2bn=log2bn+1+1 2cn=cn+1+1 2(cn-1)=cn+1-1(n≥2),
而c2-1=log2b2-1=1,
∴n≥2时,{cn-1}成首项为1,公比为2的等比数列,
∴2m2+m≥522 m≥16且m∈N*,
∴正整数m的最小值为16.
19.【答案】由题可得f = e-a,,
则f′ = e-a,
所以曲线y=f(x)在x=1处的切线方程为y-(e-a)=(e-a)(x-1),
即y=(e-a)x,
所以曲线y=f(x)在x=1处的切线恒过原点;
当0≤a<e时,f(x)没有零点;
当a<0或a=e时,f(x)有一个零点;
当a>e时,f(x)有两个零点.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某邮局有4个不同的信箱,现有5封不同的信需要邮寄,则不同的投递方法共有( )
A. 45种 B. 54种 C. C种 D. A种
2.有10台不同的电视机,其中甲型3台,乙型3台,丙型4台.现从中任意取出3台,若其中至少含有两种不同的型号,则不同的取法共有( )
A. 96种 B. 108种 C. 114种 D. 118种
3.在的二项展开式中,x的系数为( )
A. -10 B. 10 C. -40 D. 40
4.如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
A. 84 B. 72 C. 64 D. 56
5.在正项等比数列{an}中,a3a4a5=512,a7=64,若当x∈N*时,2an-8n-t≥0恒成立,则实数t的取值范围为( )
A. (-∞,16] B. (-∞,-16] C. (-∞,-20] D. (-∞,20]
6.若点P是曲线y=x2-lnx上任意一点,则点P到直线y=x-1的最小距离为( )
A. 0 B. C. D.
7.已知数列{an}满足a1=1,,,则数列{an}的前2025项的和( )
A. 31012-2025 B. 31012-2027 C. 31013-2025 D. 31013-2027
8.已知函数f(x)是定义在R上的奇函数,f(x)的图象连续,且f(1)=0,记f(x)的导函数为f′(x),若xlnx f′(x)+f(x)<0在(0,+∞)上恒成立,则使(x2-x-6)f(x)>0成立的x的取值范围是( )
A. (-2,-1)∪(-1,0)∪(0,1)∪(1,3)
B. (-∞,-2)∪(3,+∞)
C. (-2,-1)∪(-1,0)∪(3,+∞)
D. (-∞,-2)∪(0,1)∪(1,3)
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象不可能是( )
A.
B.
C.
D.
10.设函数f(x)=x2+mln(1+x)有两个极值点,则实数m的取值可以是( )
A. B. C. D.
11.设,则( )
A. a1=-2026
B.
C. a0,a1,a2, ,a2026中最大的是a1013
D.
三、填空题:本题共3小题,每小题5分,共15分。
12.曲线y=(x2-2)lnx在x=1处的切线方程为______.
13.已知,则a5= ______.
14.已知函数在区间(2,3)上存在极小值点,则实数a的取值范围为______.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
有5名同学站成一排拍照.
(1)若甲乙必须站一起,则共有多少种不同的排法?
(2)若最左端只能排甲或乙,且最右端不能排甲,则共有多少种不同的排法?
(3)求出现甲必须站正中间,并且乙、丙两位同学不能相邻的排法?
16.(本小题12分)
的展开式一共有16项.
(1)求展开式中二项式系数之和;
(2)求展开式中的常数项.
17.(本小题12分)
已知函数f(x)=xlnx+2x-1.
(1)求f(x)的单调区间;
(2)若对任意的x>1,都有f(x)-k(x-1)>0(k∈Z)恒成立,求k的最大值.
18.(本小题12分)
已知正项数列{an}满足,a1=1.数列{bn}满足各项均不为0,b1=4,其前n项的乘积.
(1)求数列{an}通项公式;
(2)设cn=log2bn,求数列{cn}的通项公式;
(3)记数列{(-1)nan}的前2m项的和S2m,求使得不等式S2m≥c1+c2+ +c10成立的正整数m的最小值.
19.(本小题12分)
已知函数.
(1)求证:对于任意实数a,曲线y=f(x)在x=1处的切线恒过原点;
(2)讨论函数f(x)的零点个数.
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】ACD
10.【答案】CD
11.【答案】AB
12.【答案】x+y-1=0
13.【答案】12
14.【答案】
15.【答案】解:(1)根据题意,将甲乙看成一个元素,再与其他3人全排列即可,
有AA=48种排法;
(2)根据题意,分2种情况讨论:
①甲在最左端,有A=24种排法,
②乙在最左端,有CA=18种排法,
则共有24+18=42种排法;
(3)根据题意,甲师必须站正中间,有1种情况,
若乙、丙两位同学不能相邻,即乙丙在甲的两边,有2×2×2×2=16种排法;
故有1×16=16种排法.
16.【答案】215; 96096.
17.【答案】解:(1)已知f(x)=xlnx+2x-1,函数的定义域为(0,+∞),
可得f′(x)=lnx+3,
当0<x<e-3时,f′(x)<0,当x>e-3时,f′(x)>0,
则函数f(x)的单调减区间为(0,e-3),单调增区间为(e-3,+∞);
(2)若对任意的x>1,都有f(x)-k(x-1)>0(k∈Z)恒成立,
即在x>1上恒成立,
不妨设,
可得,
不妨设h(x)=x-2-lnx,函数定义域为(1,+∞),
可得,
所以函数h(x)在(1,+∞)上单调递增,
又h(3)=1-ln3<0,h(4)=2-ln4>0,
所以存在唯一的x0∈(3,4),使得h(x0)=0,
此时lnx0=x0-2,
当x∈(1,x0)时,h(x)<0,g′(x)<0,g(x)单调递减;
当x∈(x0,+∞)时,h(x)>0,g′(x)>0,g(x)单调递增,
所以,
则k<x0+1∈(4,5),
又k∈Z,
故实数k的最大值为4.
18.【答案】解:(1)依题意,当n≥2时,
由an-an-1=+,
可得(+)(-)=+,
∵an>0,n∈N*,
∴+>0,
∴,
∵=1,
∴数列是以1为首项为1,1为公差的等差数列,
∴,
∴,n∈N*.
(2)由题意,当n=1时,4=b1=T1=20b2,即b2=4,
当n≥2时,由①,
可得②,
,可得,
整理,得2bn+1=,
∵当n=1时,b1=4,b2=4,2b2≠不满足上式,
∴2bn+1=,(n∈N*,n≥2),
当n≥2时,对2bn+1=两边取以2为底的对数,
可得log22bn+1=log2,
化简,得log2bn+1+1=2log2bn,
即cn+1+1=2cn,
则cn+1=2cn-1,
两边同时减1,可得cn+1-1=2cn-1-1=2(cn-1),
∵c2-1=log2b2-1=1,
∴数列{cn-1}从第二项起是以1为首项,2为公比的等比数列,
∴,
∴,
∵c1=log2b1=2,
∴.
(3)∵,
∴,
而,
∴2log2bn=log2bn+1+1 2cn=cn+1+1 2(cn-1)=cn+1-1(n≥2),
而c2-1=log2b2-1=1,
∴n≥2时,{cn-1}成首项为1,公比为2的等比数列,
∴2m2+m≥522 m≥16且m∈N*,
∴正整数m的最小值为16.
19.【答案】由题可得f = e-a,,
则f′ = e-a,
所以曲线y=f(x)在x=1处的切线方程为y-(e-a)=(e-a)(x-1),
即y=(e-a)x,
所以曲线y=f(x)在x=1处的切线恒过原点;
当0≤a<e时,f(x)没有零点;
当a<0或a=e时,f(x)有一个零点;
当a>e时,f(x)有两个零点.
第1页,共1页
同课章节目录
