第二章 实数小结与复习 课件(共30张PPT) 2025-2026学年度北师版数学八年级上册
文档属性
| 名称 | 第二章 实数小结与复习 课件(共30张PPT) 2025-2026学年度北师版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 410.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 05:57:58 | ||
图片预览








文档简介
(共30张PPT)
小结与复习
第二章 实数
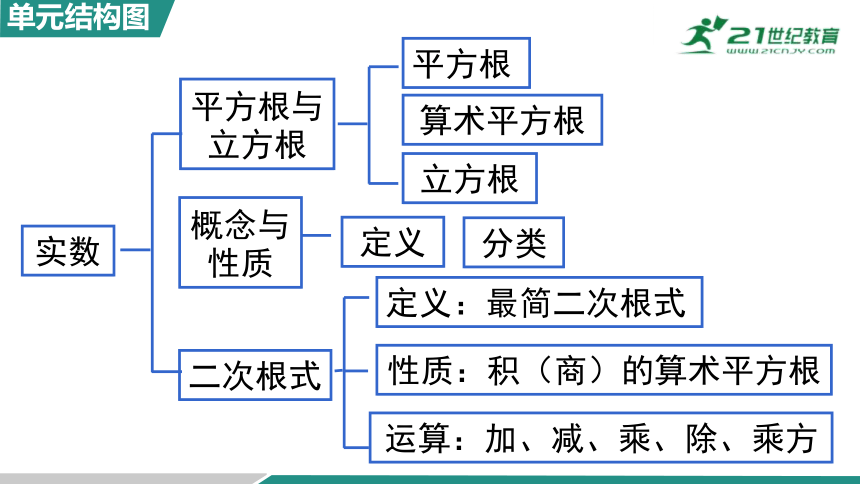
平方根与立方根
二次根式
实数
平方根
算术平方根
定义:最简二次根式
性质:积(商)的算术平方根
运算:加、减、乘、除、乘方
立方根
概念与性质
定义
分类
一、无理数
1. 无限不循环小数称为无理数.
如 π = 3.14159265…,
0.585 885 888 588 885…
(相邻两个 5 之间 8 的个数逐次加 1)
想一想:你能找到其他的无理数吗?
二、平方根与立方根
2. 算术平方根的意义:
算术平方根具有双重非负性.
非负数
≥0
(a≥0)
1. 正数 a 的正的平方根,叫作这个正数的算术平方根.
0 的算术平方根是 0 ,即
①若 ,则 x 叫 a 的平方根,即 .
②当 ,则 x 叫 a 的立方根.
即:
3. 平方根的定义:
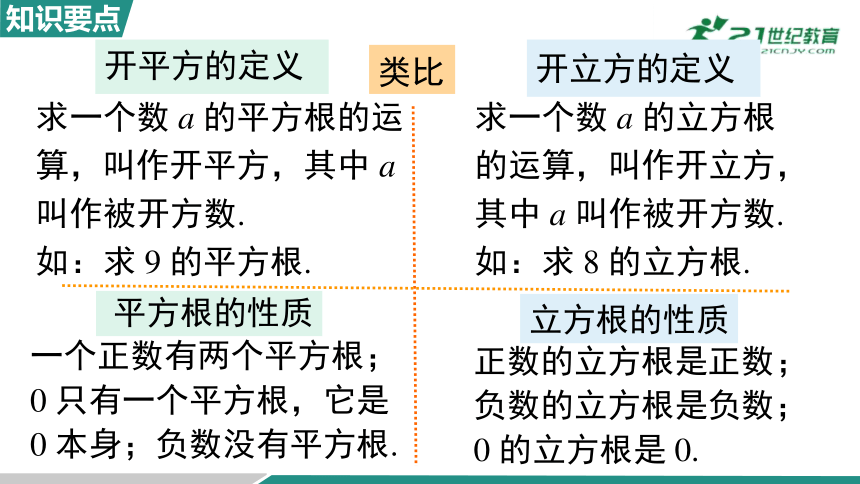
开平方的定义
类比
开立方的定义
平方根的性质
立方根的性质
求一个数 a 的立方根的运算,叫作开立方,其中 a 叫作被开方数.
如:求 8 的立方根.
一个正数有两个平方根;0 只有一个平方根,它是 0 本身;负数没有平方根.
正数的立方根是正数;
负数的立方根是负数;
0 的立方根是 0.
求一个数 a 的平方根的运算,叫作开平方,其中 a叫作被开方数.
如:求 9 的平方根.
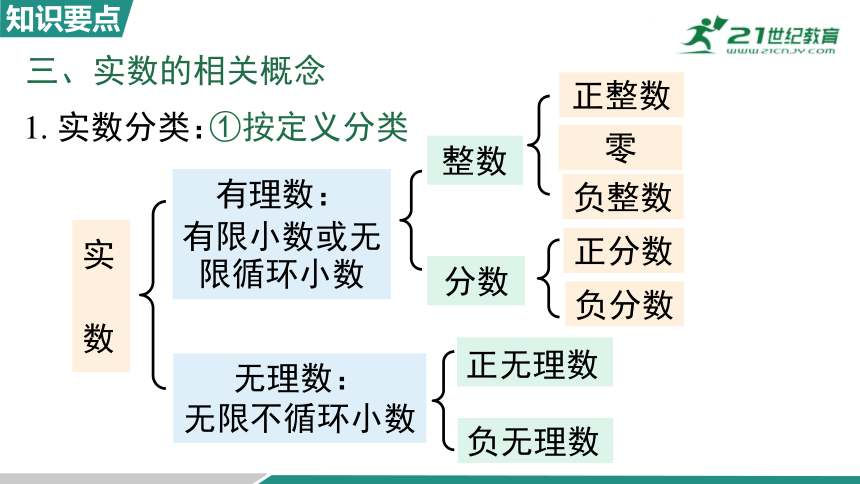
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
分数
整数
①按定义分类
正整数
零
负整数
正分数
负分数
正无理数
负无理数
三、实数的相关概念
1. 实数分类:
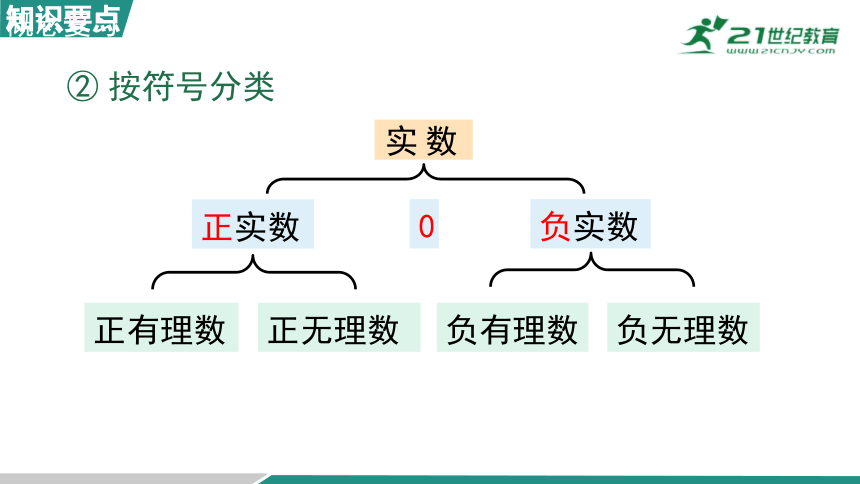
负实数
正实数
数实
正有理数
负有理数
② 按符号分类
0
正无理数
负无理数
概念复习
2. 数轴
① 实数和数轴上的点是一一对应的.
② 在数轴上,右边的点表示的数比左边的点表示的数大.
3. 相反数、倒数
a 与 -a 相反数的两数和为 0 (a与b互为相反数 a+b = 0)
b 与 互为倒数的两数积为 1 (a 与 b 互为倒数 ab = 1)
4. 绝对值(到原点的距离)
|a|=
a (a > 0)
0 (a = 0)
-a (a < 0)
|a| 为非负数,即 |a|≥0
② 非负式的常见形式有:|a|; a2; ;
5. 实数的大小比较
① 利用数轴(右边的数总比左边大);
② 作差与 0 比;
③ 作商与 1 比(分母的符号已知).
①
概念复习
四、二次根式
1、定义:
形如 的式子叫作二次根式,
2、性质:
⑴ 积的算术平方根,
等于算术平方根的积.
⑵ 商的算术平方根,
等于算术平方根的商.
其中 a 叫作被开方数.
概念复习
3、最简二次根式 :
满足以下三个条件的二次根式叫最简二次根式:
⑴被开方数不能含有开得尽方的因数或因式;
⑵被开方数不能含有分母;
⑶分母不能含有根号.
注意:
二次根式的化简与运算,最后结果应化成最简二次根式.
概念复习
4、二次根式的运算:
(1) 二次根式的加减:
类似合并同类项;
(2) 二次根式的乘法:
(3) 二次根式的除法:
(4) 二次根式的平方:
例1 下面四个数中,属于无理数的是 ( )
A. 0 B. π C. D. -3.14
B
考点一 无理数的概念
中无理数的个数是( )
A. 2 B. 3 C. 4 D. 5
A
1. 下列各数
2. 一个长方形的长与宽分别是 6、3,它的对角线的长是( )
A. 整数
D. 无理数
C. 有理数
B. 分数
D
【变式训练1】
例2 有一个数值转换器,原理如下:
当输入的 x 为 81 时, 输出的 y 是 ( )
A. 9 B. C. 3 D.
D
考点二 平方根与立方根
例3 下列说法正确的是 ( )
A. (-3)2 的平方根是 3 B. = ±4
C. 4 的算术平方根是 2 D. 9 的平方根是 3
C
3. 下列语句中正确的是( )
A.
-9 的平方根是 -3
B.
9 的平方根是 3
C.
9 的算术平方根是±3
D. 9 的算术平方根是 3
D
【变式训练2】
4. 下列运算中,正确的是( )
A
考点二 平方根与立方根
6. 下列等式正确的是( )
【变式训练3】
例4 下列结果为 -1 的是 ( )
A. B. C. D.
例5 若 ,则 a = 。
C
a = (-2)3 = -8
-8
考点二 平方根与立方根
D
例6 与 最接近的整数是 ( )
A.2 B.3 C.4 D.5
分析:32<15<42,
且 15 更接近 16,
C
例7 已知 的整数部分为 a,则 2a - 1 = .
分析:∵ 22<5<32,
∴ 的整数部分 a 为 2.
∴ 2a - 1 = 3.
3
考点二 平方根与立方根
8. 估计 的值在 ( )
A. 5 到 6 之间 B. 6 到 7 之间
C. 7 到 8 之间 D. 8 到 9 之间
C
9. 已知 a 的立方根是 2,b 是 的整数部分,
则 a + b 的算术平方根是 .
分析: a = 23 = 8
32<12<42
→ b = 3
a + b = 11
考点讲练
【变式训练4】
考点二 平方根与立方根
考点三 实数
1.实数的概念与分类
例7 将下列各数填入相应的集合中:
无理数集合:{ …};
分数集合:{ …};
正数集合:{ …};
负整数集合:{ …}。
2.实数的性质
例7 有下列语句:
① 带根号的数都是无理数;
② 任何实数的绝对值都是非负数;
③ 所有有理数都可以用数轴上的点表示,反过来,数轴上的所有点都表示有理数;
④ 若两个非负数的和为零,则这两个数都为零.
其中,错误的是 .
①③
考点三 实数
3.实数的性质与大小比较
例8 实数 a,b,c,d 在数轴上的对应点如图所示,则
将它们用“ < ”连接是 .
c d 0 b a
其中:
c < d < b < a
a + b
-d - c
b - c
a - d
| c-b|=
| a-d|=
考点三 实数
11. 比较大小: 与
解:∵ (-2 + )-(-2+ ) = -2+ +2- = - >0,
∴ -2+ >-2+
另解:直接由正负决定-2+ >-2+
【变式训练5】
考点三 实数
4.实数的运算
例9 计算:
(2) 原式
解:(1) 原式 = 3 + 1 - 3 + 6
= 7.
= -1.
考点三 实数
1.二次根式有意义的条件
例10 若要使 有意义,则 x 的取值范围为 .
分析:被开方数为非负数
分母不为 0
→ x - 4 ≠ 0
x≤3
→ 3 - x ≥ 0
x≤3
考点四 二次根式
13. 已知 ,那么 xy = .
分析:被开方数为非负数
2x - 1≥0,1 - 2x≥0,
∴ y = 2.
1
考点四 二次根式
2.二次根式的化简
例11 下列各式中,计算正确的是 ( )
C
(a≥0)
考点讲练
考点四 二次根式
14. 先化简再求值:当 a = 时,
求 的值.
解:原式
当 a = 时,
原式
考点四 二次根式
考点讲练
3.二次根式的运算
例12 计算:
解:(1) 原式
(2) 原式
考点四 二次根式
15. 计算:
解:(1) 原式 =
(2) 原式 =
= 6 - 5
= 1.
= 5 + 1
= 6.
考点讲练
考点四 二次根式
小结与复习
第二章 实数
平方根与立方根
二次根式
实数
平方根
算术平方根
定义:最简二次根式
性质:积(商)的算术平方根
运算:加、减、乘、除、乘方
立方根
概念与性质
定义
分类
一、无理数
1. 无限不循环小数称为无理数.
如 π = 3.14159265…,
0.585 885 888 588 885…
(相邻两个 5 之间 8 的个数逐次加 1)
想一想:你能找到其他的无理数吗?
二、平方根与立方根
2. 算术平方根的意义:
算术平方根具有双重非负性.
非负数
≥0
(a≥0)
1. 正数 a 的正的平方根,叫作这个正数的算术平方根.
0 的算术平方根是 0 ,即
①若 ,则 x 叫 a 的平方根,即 .
②当 ,则 x 叫 a 的立方根.
即:
3. 平方根的定义:
开平方的定义
类比
开立方的定义
平方根的性质
立方根的性质
求一个数 a 的立方根的运算,叫作开立方,其中 a 叫作被开方数.
如:求 8 的立方根.
一个正数有两个平方根;0 只有一个平方根,它是 0 本身;负数没有平方根.
正数的立方根是正数;
负数的立方根是负数;
0 的立方根是 0.
求一个数 a 的平方根的运算,叫作开平方,其中 a叫作被开方数.
如:求 9 的平方根.
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
分数
整数
①按定义分类
正整数
零
负整数
正分数
负分数
正无理数
负无理数
三、实数的相关概念
1. 实数分类:
负实数
正实数
数实
正有理数
负有理数
② 按符号分类
0
正无理数
负无理数
概念复习
2. 数轴
① 实数和数轴上的点是一一对应的.
② 在数轴上,右边的点表示的数比左边的点表示的数大.
3. 相反数、倒数
a 与 -a 相反数的两数和为 0 (a与b互为相反数 a+b = 0)
b 与 互为倒数的两数积为 1 (a 与 b 互为倒数 ab = 1)
4. 绝对值(到原点的距离)
|a|=
a (a > 0)
0 (a = 0)
-a (a < 0)
|a| 为非负数,即 |a|≥0
② 非负式的常见形式有:|a|; a2; ;
5. 实数的大小比较
① 利用数轴(右边的数总比左边大);
② 作差与 0 比;
③ 作商与 1 比(分母的符号已知).
①
概念复习
四、二次根式
1、定义:
形如 的式子叫作二次根式,
2、性质:
⑴ 积的算术平方根,
等于算术平方根的积.
⑵ 商的算术平方根,
等于算术平方根的商.
其中 a 叫作被开方数.
概念复习
3、最简二次根式 :
满足以下三个条件的二次根式叫最简二次根式:
⑴被开方数不能含有开得尽方的因数或因式;
⑵被开方数不能含有分母;
⑶分母不能含有根号.
注意:
二次根式的化简与运算,最后结果应化成最简二次根式.
概念复习
4、二次根式的运算:
(1) 二次根式的加减:
类似合并同类项;
(2) 二次根式的乘法:
(3) 二次根式的除法:
(4) 二次根式的平方:
例1 下面四个数中,属于无理数的是 ( )
A. 0 B. π C. D. -3.14
B
考点一 无理数的概念
中无理数的个数是( )
A. 2 B. 3 C. 4 D. 5
A
1. 下列各数
2. 一个长方形的长与宽分别是 6、3,它的对角线的长是( )
A. 整数
D. 无理数
C. 有理数
B. 分数
D
【变式训练1】
例2 有一个数值转换器,原理如下:
当输入的 x 为 81 时, 输出的 y 是 ( )
A. 9 B. C. 3 D.
D
考点二 平方根与立方根
例3 下列说法正确的是 ( )
A. (-3)2 的平方根是 3 B. = ±4
C. 4 的算术平方根是 2 D. 9 的平方根是 3
C
3. 下列语句中正确的是( )
A.
-9 的平方根是 -3
B.
9 的平方根是 3
C.
9 的算术平方根是±3
D. 9 的算术平方根是 3
D
【变式训练2】
4. 下列运算中,正确的是( )
A
考点二 平方根与立方根
6. 下列等式正确的是( )
【变式训练3】
例4 下列结果为 -1 的是 ( )
A. B. C. D.
例5 若 ,则 a = 。
C
a = (-2)3 = -8
-8
考点二 平方根与立方根
D
例6 与 最接近的整数是 ( )
A.2 B.3 C.4 D.5
分析:32<15<42,
且 15 更接近 16,
C
例7 已知 的整数部分为 a,则 2a - 1 = .
分析:∵ 22<5<32,
∴ 的整数部分 a 为 2.
∴ 2a - 1 = 3.
3
考点二 平方根与立方根
8. 估计 的值在 ( )
A. 5 到 6 之间 B. 6 到 7 之间
C. 7 到 8 之间 D. 8 到 9 之间
C
9. 已知 a 的立方根是 2,b 是 的整数部分,
则 a + b 的算术平方根是 .
分析: a = 23 = 8
32<12<42
→ b = 3
a + b = 11
考点讲练
【变式训练4】
考点二 平方根与立方根
考点三 实数
1.实数的概念与分类
例7 将下列各数填入相应的集合中:
无理数集合:{ …};
分数集合:{ …};
正数集合:{ …};
负整数集合:{ …}。
2.实数的性质
例7 有下列语句:
① 带根号的数都是无理数;
② 任何实数的绝对值都是非负数;
③ 所有有理数都可以用数轴上的点表示,反过来,数轴上的所有点都表示有理数;
④ 若两个非负数的和为零,则这两个数都为零.
其中,错误的是 .
①③
考点三 实数
3.实数的性质与大小比较
例8 实数 a,b,c,d 在数轴上的对应点如图所示,则
将它们用“ < ”连接是 .
c d 0 b a
其中:
c < d < b < a
a + b
-d - c
b - c
a - d
| c-b|=
| a-d|=
考点三 实数
11. 比较大小: 与
解:∵ (-2 + )-(-2+ ) = -2+ +2- = - >0,
∴ -2+ >-2+
另解:直接由正负决定-2+ >-2+
【变式训练5】
考点三 实数
4.实数的运算
例9 计算:
(2) 原式
解:(1) 原式 = 3 + 1 - 3 + 6
= 7.
= -1.
考点三 实数
1.二次根式有意义的条件
例10 若要使 有意义,则 x 的取值范围为 .
分析:被开方数为非负数
分母不为 0
→ x - 4 ≠ 0
x≤3
→ 3 - x ≥ 0
x≤3
考点四 二次根式
13. 已知 ,那么 xy = .
分析:被开方数为非负数
2x - 1≥0,1 - 2x≥0,
∴ y = 2.
1
考点四 二次根式
2.二次根式的化简
例11 下列各式中,计算正确的是 ( )
C
(a≥0)
考点讲练
考点四 二次根式
14. 先化简再求值:当 a = 时,
求 的值.
解:原式
当 a = 时,
原式
考点四 二次根式
考点讲练
3.二次根式的运算
例12 计算:
解:(1) 原式
(2) 原式
考点四 二次根式
15. 计算:
解:(1) 原式 =
(2) 原式 =
= 6 - 5
= 1.
= 5 + 1
= 6.
考点讲练
考点四 二次根式
同课章节目录
