八年级上册数学第一次月考调研检测试卷(含答案)苏科版2025—2026学年
文档属性
| 名称 | 八年级上册数学第一次月考调研检测试卷(含答案)苏科版2025—2026学年 |  | |
| 格式 | docx | ||
| 文件大小 | 995.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 15:46:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级上册数学第一次月考调研检测试卷苏科版2025—2026学年
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,不是轴对称图形的是( )
A.B.C.D.
2.在联欢晚会上,有、、三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边上高的交点 D.三条垂直平分线的交点
3.下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
4.如图,∠A=∠D,BC=EF,要得到△ABC≌△DEF,可以添加( )
A.DE//AB B.EF//BC C.AB=DE D.AC=DF
5.如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为( )
A.30° B.50° C.90° D.100°
6.请仔细观察用直尺和圆规作一个角等于已知角的示意图如图所示,请你根据所学的三角形全等有关的知识,说明画出的依据是( )
A. B. C. D.
7.已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为( ).
A.100° B.40° C.40°或100° D.40°或70°
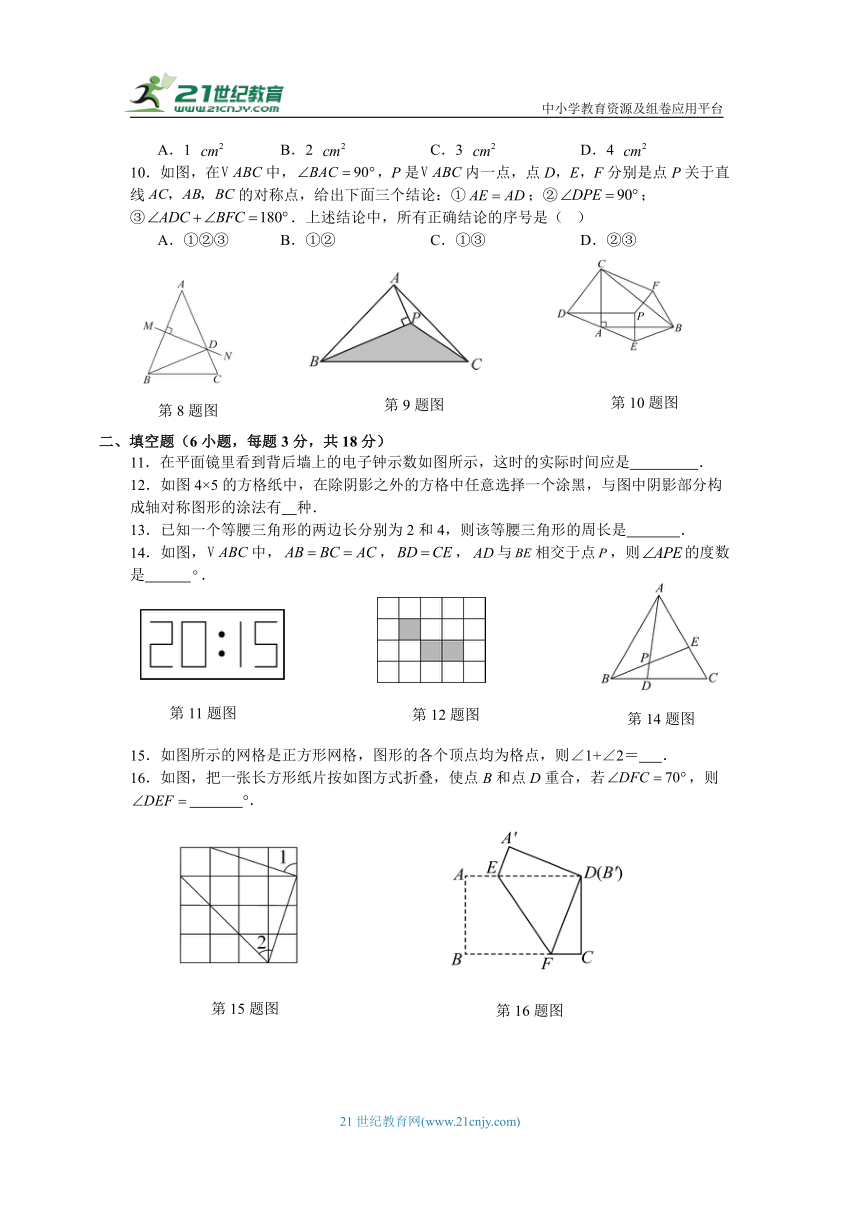
8.如图,在△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交于AC于D点,则∠DBC的度数是 ( )
A.15° B.20° C.25° D.30°
9.如图,的面积为,AP垂直∠B的平分线BP于P,则的面积为( )
A.1 B.2 C.3 D.4
10.如图,在中,,P是内一点,点D,E,F分别是点P关于直线的对称点,给出下面三个结论:①;②;③.上述结论中,所有正确结论的序号是( )
A.①②③ B.①② C.①③ D.②③
二、填空题(6小题,每题3分,共18分)
11.在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应是 .
12.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有 种.
13.已知一个等腰三角形的两边长分别为2和4,则该等腰三角形的周长是 .
14.如图,中,,,与相交于点,则的度数是 .
15.如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2= .
16.如图,把一张长方形纸片按如图方式折叠,使点B和点D重合,若,则 °.
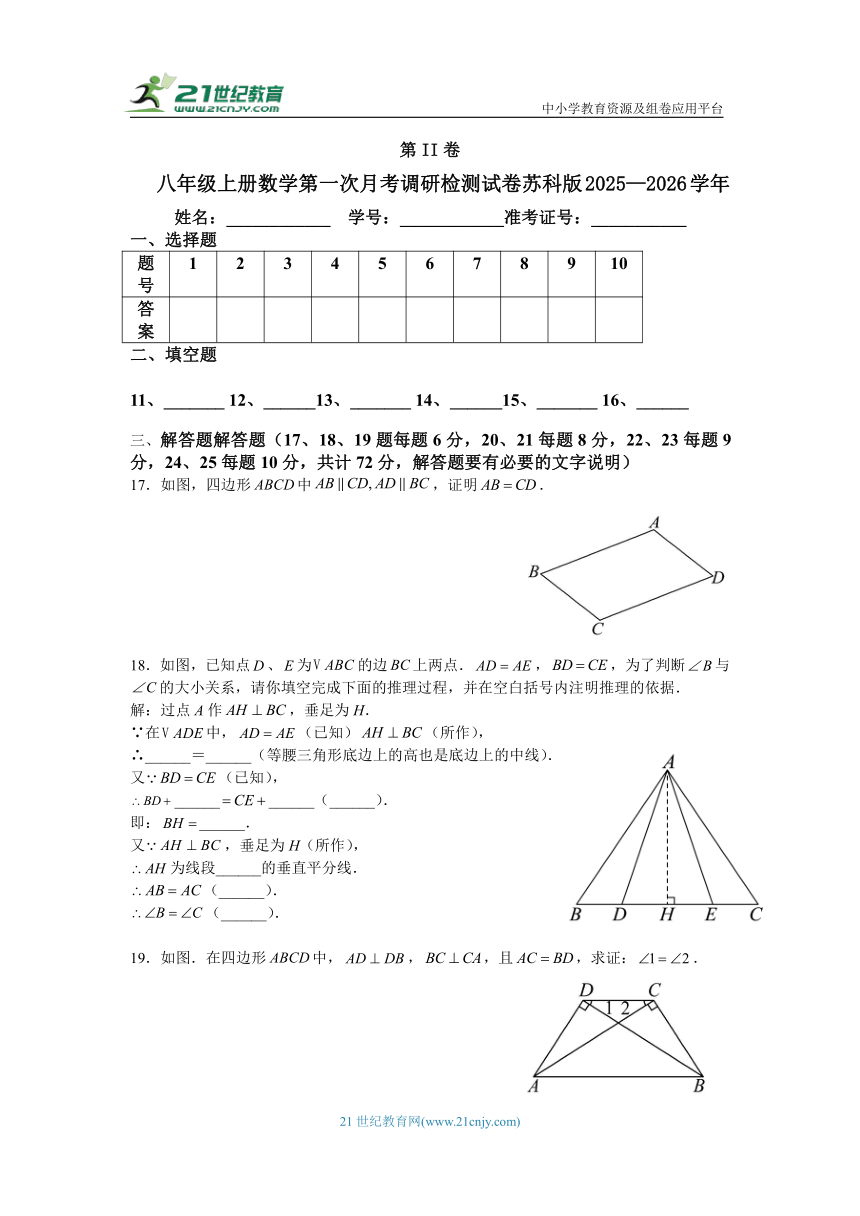
第II卷
八年级上册数学第一次月考调研检测试卷苏科版2025—2026学年
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.如图,四边形中,证明.
18.如图,已知点、为的边上两点.,,为了判断与的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.
解:过点A作,垂足为H.
∵在中,(已知)(所作),
∴______=______(等腰三角形底边上的高也是底边上的中线).
又(已知),
____________(______).
即:______.
又,垂足为H(所作),
为线段______的垂直平分线.
(______).
(______).
19.如图.在四边形中,,,且,求证:.
20.如图,在正方形网格中,点,,,,都在格点上.
(1)作关于直线对称的图形;
(2)若网格中最小正方形边长为1,求的面积;
(3)在直线上找一点,使得的值最大,并画出点的位置.
21.如图,在中,,于E,点F在边上.
(1)求证:;
(2)若,且的面积等于6,求的长.
22.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,求△ADE的周长;
(2) 设直线DM、EN交于点O
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数
23.【问题背景】
如图,在中,,和的平分线和相交于点 G.
【问题探究】
(1)的度数为 ;
(2)过G作交的延长线于点 F,交于点 H,判断与的数量关系,并说明理由;
(3)在(2)的条件下,若,求的长.
24.已知:中,,,D为直线上一动点,连接,在直线右侧作,且.
(1)如图1,当点在线段上时,过点作于.求证:;
(2)如图2,当点在线段的延长线上时,连接交的延长线于点M.求证:;
(3)当点在直线上时,连接交直线于,若,则___.(直接写出结果)
25.如图,在中,,D为直线上一动点(不与点B,C重合),在的右侧作,使得,连接.
(1)当D在线段上时,求证:.
(2)请判断点D在何处时,,并说明理由.
(3)当时,若中最小角为,直接写出的度数.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B B D C C A B B
二、填空题
11.【解】根据镜面对称的性质,题中所显示的时刻与成轴对称,所以此时实际时刻为:.
故答案为:.
12.【解】根据轴对称图形的概念可知,一共有四种涂法,如下图所示:
故答案为4.
13.【解】解:因为2+2=4,
所以腰长为2时不能构成三角形;
所以等腰三角形的腰的长度是4,底边长2,
周长:4+4+2=10,
答:它的周长是10,
故答案为:10.
14.【解】解:∵,
∴是等边三角形,
∴,
在和中,
,
,
,
,,
.
故答案为:
15.【解】解:如图所示:
可知:AB=CD=3,BC=DE=1,∠B=∠D=90°,
∴△ABC≌△CDE(SAS),
∴∠1=∠3,
则∠1+∠2=∠2+∠3=135°.
故答案为:135°.
16.【解】解:如图,由折叠的性质知:.
∵,,
∴.
又,
∴.
故答案为:55.
三、解答题
17.【解】证明:连接,
,
,
又,
在与中
,
,
.
18.【解】解:过点作,垂足为.
在中,(已知),(所作),
,(等腰三角形底边上的高也是底边上的中线).
又(已知),
(等式的性质).
即:.
又,垂足为(所作),
为线段的垂直平分线.
(线段垂直平分线的性质).
(同一个三角形中,等边对等角).
故答案为:;;;;等式的性质;;;线段垂直平分线的性质;同一个三角形中,等边对等角.
19.【解】证明:,,
在和中,
,
,
,
在和中,
,
,
.
20.【解】(1)如图,即为所求.
(2)的面积为
(3)点P即为所求
21.【解】(1)证明:∵
∴
∴
在和中,
,
∴,
∴;
(2)解:∵,,
而
,
∴,
∴.
22.【解】(1)∵在△ABC中,AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE,
又∵BC=10,
∴△ADE周长为:AD+DE+AE=BD+DE+EC=BC=10;
(2)①如图,连接OB,OA,OC,
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴BO=AO,CO=AO,
∴BO=CO,
∴O在BC的垂直平分线上;
②∵OM⊥AB,ON⊥AC,
∴∠AMO=∠ANO=90°,
∵∠BAC=100°,
∴∠MOM=360°-∠AMO-∠BAC-∠ANO=80°;
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴∠BOM=∠AOM,∠CON=∠AON,
∴∠BOC=2∠MON=160°.
23.【解】(1)解:∵在中,,
∴,
∵和的平分线和相交于点 G,
∴,
∴,
∴,
故答案为:;
(2)解:,理由如下:
∵,
∴,
∵,
∴,
又∵,
∴,
∵和的平分线和相交于点 G,
∴,
∴,
又∵,
∴,
∴;
(3)解:∵,
∴,
∴,
又∵,
∴,
∴.
24.【解】(1)证明:∵,,
∴,,
∵,
∴,
又∵,,
∴,
∴;
(2)证明:如图2,作的延长线于,
同理(1),,
∴,
∴,
又∵,,
∴,
∴;
(3)解:∵,
∴,
由题意知,分在线段上,在的延长线上两种情况求解;
当在线段上时,如图3,作的延长线于,
同理(1),,
∴,,
∴,
同理(2),,
∴,
设,则,,
∴,
∴,
∴;
当在的延长线上时,如图4,作的延长线于,
同理, ,,
设,则,,
∴,
∴,
∴;
综上所述,的值为4或,
故答案为:4或.
25.【解】(1)证明:∵,
∴,
在和中,
,
∴;
(2)解:若,
又∵,
∴平分,
∴,
∴平分,
又∵,
∴,
∴当点D在中点时,;
(3)解:由(1)可知,
∴,
当时,则,,
∵,
∴,
∴,
∴为等边三角形,
①如图1:D在线段上时,若,
则.
②如图2,点D在的延长线上,,
③如图3,点D在的延长线上,此时,.
④如图4,.
综上所述,满足条件的的度数为或或.
21世纪教育网(www.21cnjy.com)
八年级上册数学第一次月考调研检测试卷苏科版2025—2026学年
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,不是轴对称图形的是( )
A.B.C.D.
2.在联欢晚会上,有、、三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边上高的交点 D.三条垂直平分线的交点
3.下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
4.如图,∠A=∠D,BC=EF,要得到△ABC≌△DEF,可以添加( )
A.DE//AB B.EF//BC C.AB=DE D.AC=DF
5.如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为( )
A.30° B.50° C.90° D.100°
6.请仔细观察用直尺和圆规作一个角等于已知角的示意图如图所示,请你根据所学的三角形全等有关的知识,说明画出的依据是( )
A. B. C. D.
7.已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为( ).
A.100° B.40° C.40°或100° D.40°或70°
8.如图,在△ABC中,AB=AC,∠C=65°,AB的垂直平分线MN交于AC于D点,则∠DBC的度数是 ( )
A.15° B.20° C.25° D.30°
9.如图,的面积为,AP垂直∠B的平分线BP于P,则的面积为( )
A.1 B.2 C.3 D.4
10.如图,在中,,P是内一点,点D,E,F分别是点P关于直线的对称点,给出下面三个结论:①;②;③.上述结论中,所有正确结论的序号是( )
A.①②③ B.①② C.①③ D.②③
二、填空题(6小题,每题3分,共18分)
11.在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应是 .
12.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有 种.
13.已知一个等腰三角形的两边长分别为2和4,则该等腰三角形的周长是 .
14.如图,中,,,与相交于点,则的度数是 .
15.如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2= .
16.如图,把一张长方形纸片按如图方式折叠,使点B和点D重合,若,则 °.
第II卷
八年级上册数学第一次月考调研检测试卷苏科版2025—2026学年
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.如图,四边形中,证明.
18.如图,已知点、为的边上两点.,,为了判断与的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.
解:过点A作,垂足为H.
∵在中,(已知)(所作),
∴______=______(等腰三角形底边上的高也是底边上的中线).
又(已知),
____________(______).
即:______.
又,垂足为H(所作),
为线段______的垂直平分线.
(______).
(______).
19.如图.在四边形中,,,且,求证:.
20.如图,在正方形网格中,点,,,,都在格点上.
(1)作关于直线对称的图形;
(2)若网格中最小正方形边长为1,求的面积;
(3)在直线上找一点,使得的值最大,并画出点的位置.
21.如图,在中,,于E,点F在边上.
(1)求证:;
(2)若,且的面积等于6,求的长.
22.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,求△ADE的周长;
(2) 设直线DM、EN交于点O
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数
23.【问题背景】
如图,在中,,和的平分线和相交于点 G.
【问题探究】
(1)的度数为 ;
(2)过G作交的延长线于点 F,交于点 H,判断与的数量关系,并说明理由;
(3)在(2)的条件下,若,求的长.
24.已知:中,,,D为直线上一动点,连接,在直线右侧作,且.
(1)如图1,当点在线段上时,过点作于.求证:;
(2)如图2,当点在线段的延长线上时,连接交的延长线于点M.求证:;
(3)当点在直线上时,连接交直线于,若,则___.(直接写出结果)
25.如图,在中,,D为直线上一动点(不与点B,C重合),在的右侧作,使得,连接.
(1)当D在线段上时,求证:.
(2)请判断点D在何处时,,并说明理由.
(3)当时,若中最小角为,直接写出的度数.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B B D C C A B B
二、填空题
11.【解】根据镜面对称的性质,题中所显示的时刻与成轴对称,所以此时实际时刻为:.
故答案为:.
12.【解】根据轴对称图形的概念可知,一共有四种涂法,如下图所示:
故答案为4.
13.【解】解:因为2+2=4,
所以腰长为2时不能构成三角形;
所以等腰三角形的腰的长度是4,底边长2,
周长:4+4+2=10,
答:它的周长是10,
故答案为:10.
14.【解】解:∵,
∴是等边三角形,
∴,
在和中,
,
,
,
,,
.
故答案为:
15.【解】解:如图所示:
可知:AB=CD=3,BC=DE=1,∠B=∠D=90°,
∴△ABC≌△CDE(SAS),
∴∠1=∠3,
则∠1+∠2=∠2+∠3=135°.
故答案为:135°.
16.【解】解:如图,由折叠的性质知:.
∵,,
∴.
又,
∴.
故答案为:55.
三、解答题
17.【解】证明:连接,
,
,
又,
在与中
,
,
.
18.【解】解:过点作,垂足为.
在中,(已知),(所作),
,(等腰三角形底边上的高也是底边上的中线).
又(已知),
(等式的性质).
即:.
又,垂足为(所作),
为线段的垂直平分线.
(线段垂直平分线的性质).
(同一个三角形中,等边对等角).
故答案为:;;;;等式的性质;;;线段垂直平分线的性质;同一个三角形中,等边对等角.
19.【解】证明:,,
在和中,
,
,
,
在和中,
,
,
.
20.【解】(1)如图,即为所求.
(2)的面积为
(3)点P即为所求
21.【解】(1)证明:∵
∴
∴
在和中,
,
∴,
∴;
(2)解:∵,,
而
,
∴,
∴.
22.【解】(1)∵在△ABC中,AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE,
又∵BC=10,
∴△ADE周长为:AD+DE+AE=BD+DE+EC=BC=10;
(2)①如图,连接OB,OA,OC,
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴BO=AO,CO=AO,
∴BO=CO,
∴O在BC的垂直平分线上;
②∵OM⊥AB,ON⊥AC,
∴∠AMO=∠ANO=90°,
∵∠BAC=100°,
∴∠MOM=360°-∠AMO-∠BAC-∠ANO=80°;
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴∠BOM=∠AOM,∠CON=∠AON,
∴∠BOC=2∠MON=160°.
23.【解】(1)解:∵在中,,
∴,
∵和的平分线和相交于点 G,
∴,
∴,
∴,
故答案为:;
(2)解:,理由如下:
∵,
∴,
∵,
∴,
又∵,
∴,
∵和的平分线和相交于点 G,
∴,
∴,
又∵,
∴,
∴;
(3)解:∵,
∴,
∴,
又∵,
∴,
∴.
24.【解】(1)证明:∵,,
∴,,
∵,
∴,
又∵,,
∴,
∴;
(2)证明:如图2,作的延长线于,
同理(1),,
∴,
∴,
又∵,,
∴,
∴;
(3)解:∵,
∴,
由题意知,分在线段上,在的延长线上两种情况求解;
当在线段上时,如图3,作的延长线于,
同理(1),,
∴,,
∴,
同理(2),,
∴,
设,则,,
∴,
∴,
∴;
当在的延长线上时,如图4,作的延长线于,
同理, ,,
设,则,,
∴,
∴,
∴;
综上所述,的值为4或,
故答案为:4或.
25.【解】(1)证明:∵,
∴,
在和中,
,
∴;
(2)解:若,
又∵,
∴平分,
∴,
∴平分,
又∵,
∴,
∴当点D在中点时,;
(3)解:由(1)可知,
∴,
当时,则,,
∵,
∴,
∴,
∴为等边三角形,
①如图1:D在线段上时,若,
则.
②如图2,点D在的延长线上,,
③如图3,点D在的延长线上,此时,.
④如图4,.
综上所述,满足条件的的度数为或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
