八年级上册数学期中考试全真模拟试卷(含答案)苏科版2025—2026学年
文档属性
| 名称 | 八年级上册数学期中考试全真模拟试卷(含答案)苏科版2025—2026学年 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
八年级上册数学期中考试全真模拟试卷苏科版2025—2026学年
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.49的平方根为( )
A.7 B.-7 C.±7 D.±
2.以下是清华大学、北京大学、上海交通大学、中国人民大学四个大学的校徽,其中是轴对称图形的是( )
A.B. C. D.
3.我国是最早了解勾股定理的国家之一,它被记载于我国古代著名的数学著作《周髀算经》中,下列各组数中,是“勾股数”的是( )
A.1,1,2 B.1,,2 C.3,4,5 D.,,
4.下列条件不能判定△ABC是直角三角形的是( )
A. B.
C. D.
5.若,则的取值范围是( )
A. B. C. D.
6.下列运算正确的是( )
A.±5 B. C.2 D.4
7.数字中有理数的个数是( )
A.1 B.2 C.3 D.4
8.在的边上找一点P,使得.下面找法正确的是( )
A.B.C.D.
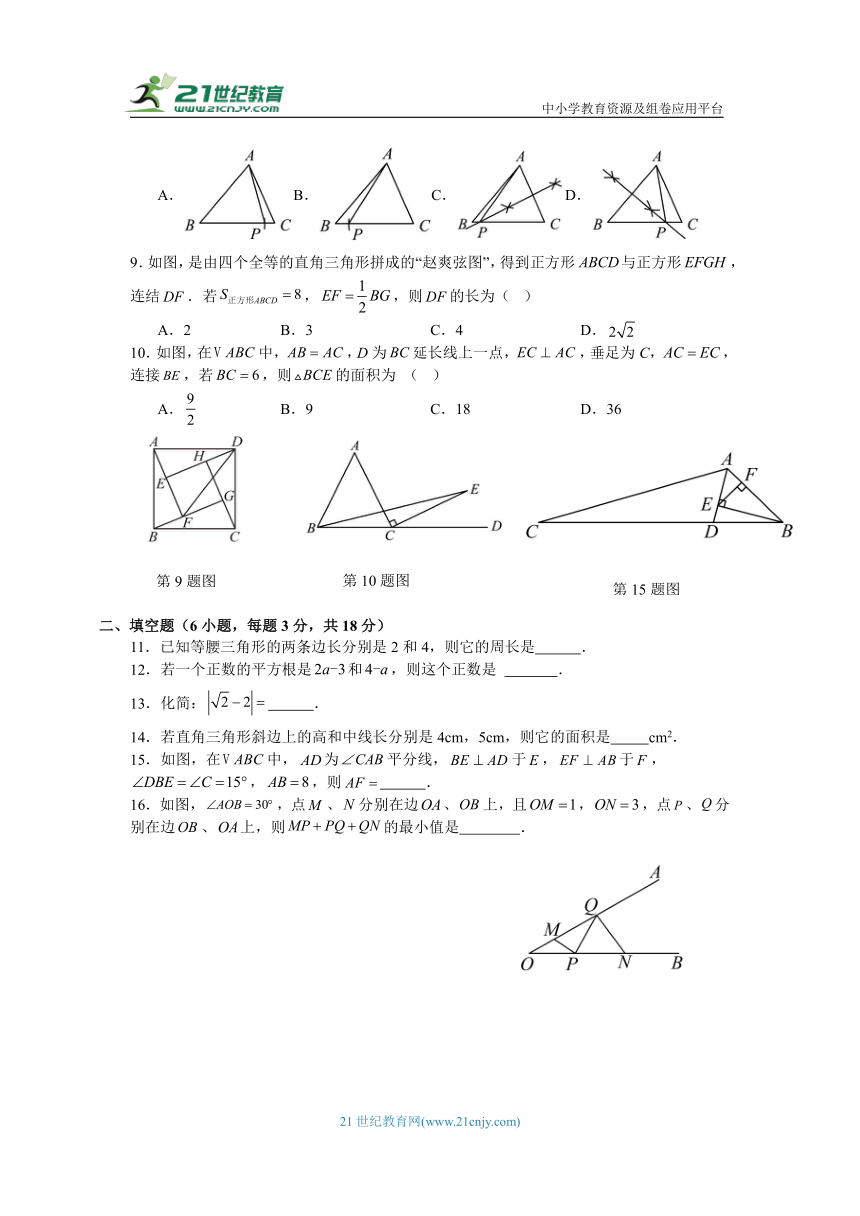
9.如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形与正方形,连结.若,,则的长为( )
A.2 B.3 C.4 D.
10.如图,在中,,D为延长线上一点,,垂足为C,,连接,若,则的面积为 ( )
A. B.9 C.18 D.36
二、填空题(6小题,每题3分,共18分)
11.已知等腰三角形的两条边长分别是2和4,则它的周长是 .
12.若一个正数的平方根是和,则这个正数是 .
13.化简: .
14.若直角三角形斜边上的高和中线长分别是4cm,5cm,则它的面积是 cm2.
15.如图,在中,为平分线,于,于,,,则 .
16.如图,,点、分别在边、上,且,,点、分别在边、上,则的最小值是 .
第II卷
八年级上册数学期中考试全真模拟试卷苏科版2025—2026学年
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
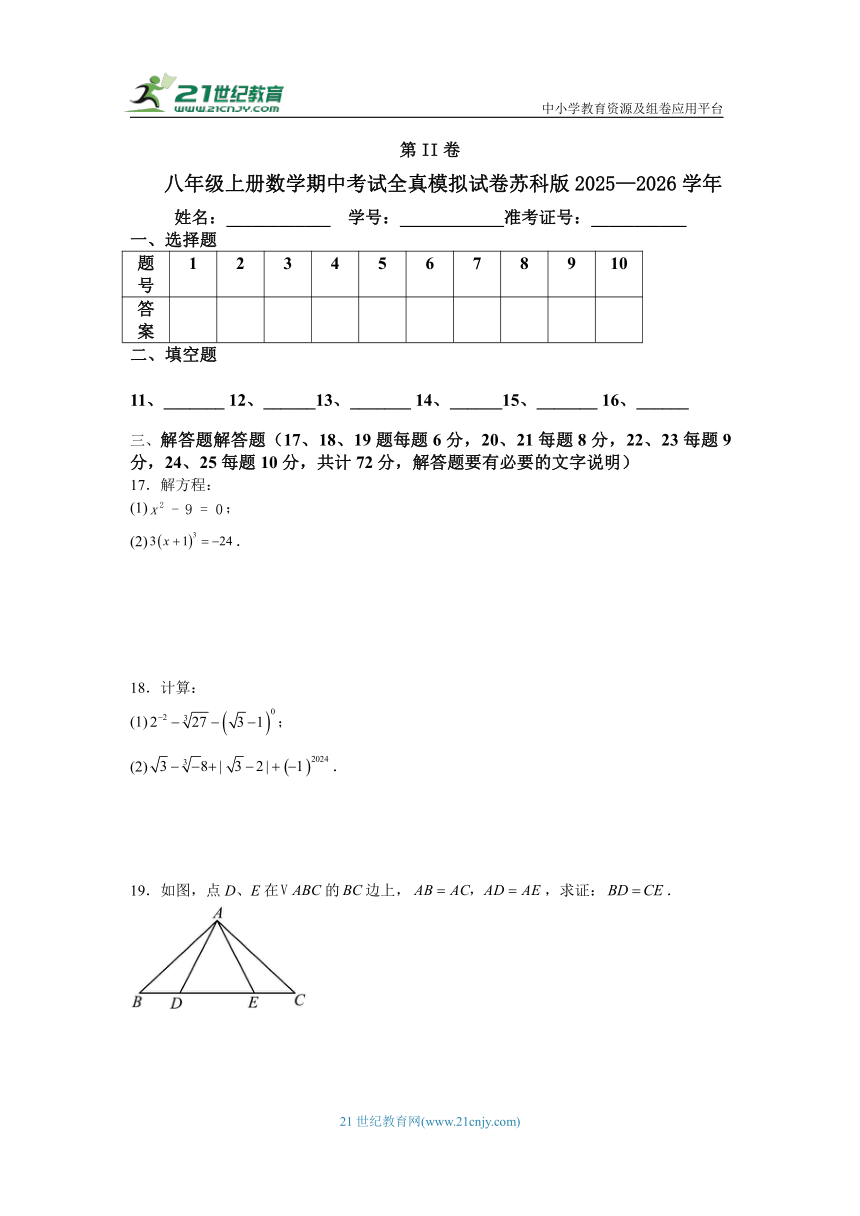
17.解方程:
(1);
(2).
18.计算:
(1);
(2).
19.如图,点D、E在的边上,,求证:.
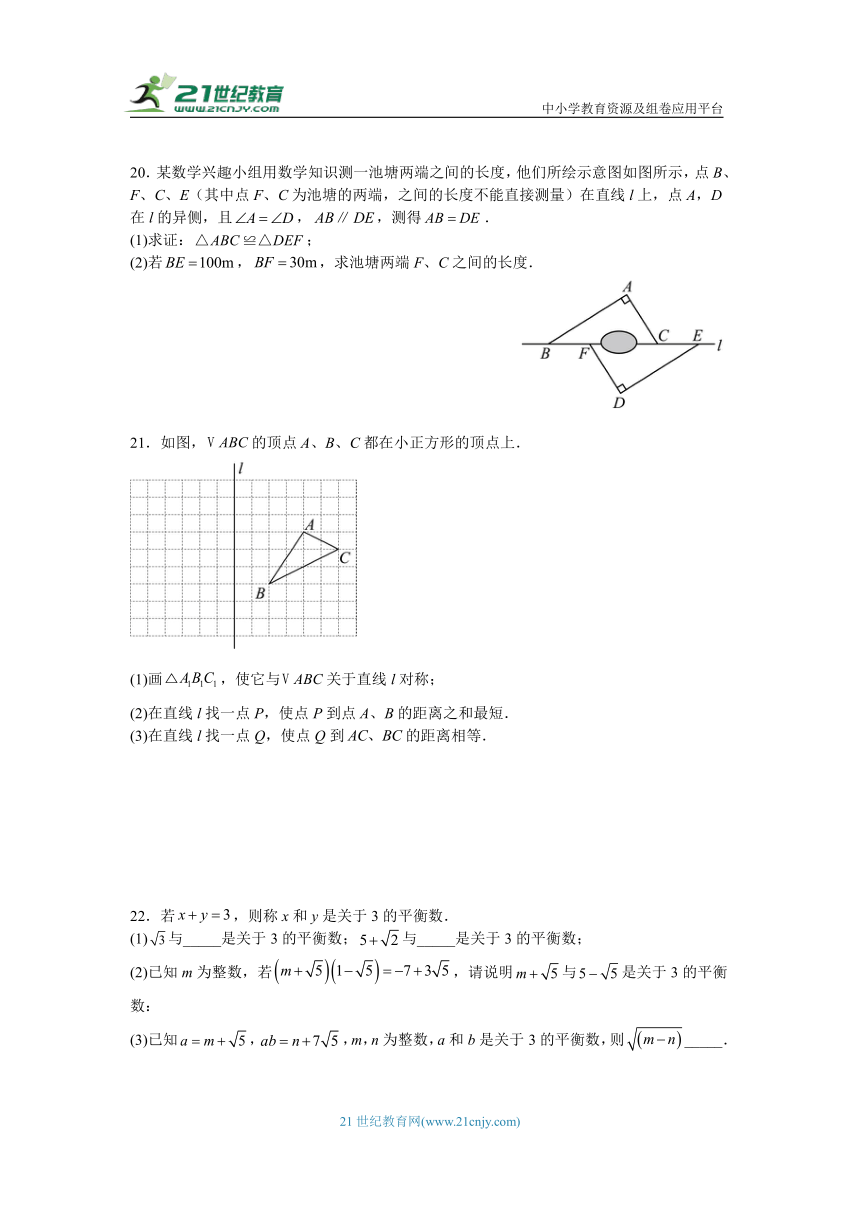
20.某数学兴趣小组用数学知识测一池塘两端之间的长度,他们所绘示意图如图所示,点B、F、C、E(其中点F、C为池塘的两端,之间的长度不能直接测量)在直线l上,点A,D在l的异侧,且,,测得.
(1)求证:;
(2)若,,求池塘两端F、C之间的长度.
21.如图,的顶点A、B、C都在小正方形的顶点上.
(1)画,使它与关于直线l对称;
(2)在直线l找一点P,使点P到点A、B的距离之和最短.
(3)在直线l找一点Q,使点Q到的距离相等.
22.若,则称x和y是关于3的平衡数.
(1)与_____是关于3的平衡数;与_____是关于3的平衡数;
(2)已知m为整数,若,请说明与是关于3的平衡数:
(3)已知,,m,n为整数,a和b是关于3的平衡数,则_____.
23.如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a.较短的直角边为b,斜边长为c,结合图①,试验证勾股定理;
(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓线的周长为80,,求该飞镖状图案的面积;
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形,正方形,正方形的面积分别为、、,若,求.
24.如图,中,,,过点任作一条直线,将线段沿直线翻折得线段,直线交直线于点,直线交直线于点.
(1)设,则______(用含m的代数式表示),并证明:;
(2)猜想线段、、之间的数量关系,并给出证明.
(3)若,,求的面积.
25.如图,在中,点在边上,,的平分线交于点,过点作,垂足为,且,连接.
(1)求的度数;
(2)求证:平分;
(3)若,,,且,求的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A B D D D D B
二、填空题
11.【解】解:当2为腰时,三边为2,2,4,由三角形三边关系定理可知,不能构成三角形,
当4为腰时,三边为4,4,2,符合三角形三边关系定理,周长为:4+4+2=10.
故答案为:10.
12.【解】解:根据题意得,,
解得,
,
∴这个正数是,
故答案为: 25.
13.【解】解:∵,
∴,
∴
∴.
故答案为:.
14.【解】解:由直角三角形斜边中线等于斜边的一半,可知斜边长为2×5=10cm,
所以它的面积是:×10×4=20(cm2);
故答案为:20
15.【解】解:
,
,
,
,,
,
为平分线,
,
于,
,,
设,则,,
,即,
解得:,
,
故答案为:.
16.【解】解:如图,作点关于的对称点,作点关于的对称点,连接,
由轴对称的性质得:,,,
∴,,
由两点之间线段最短可知,当点共线时,的值最小,最小值为,
即的最小值是,
故答案为:.
三、解答题
17.【解】(1)解:,
,
∴;
(2)解:,
,
,
∴.
18.【解】(1)解:
;
(2)解:
19.【解】证明:如图,过点A作C于P.
∵
∴;
∵,
∴,
∴,
∴.
20.【解】(1)证明:∵,
∴,
在与中,
,
;
(2)解:,
,
,
池塘两端F、C之间的长度是
21.【解】(1)解:如图,即为所求作.
(2)解:如图,点P即为所求作.
理由:根据(1)的结论,点A、点关于直线l成轴对称,
∴,
∴,
∴当点P在直线l和交点处时,,为最小值,
∴当点P在直线l和的交点处时,取最小值,
即点P到点A、点B的距离之和最短;
(3)解:如图,点Q即为所求作.
22.【解】(1)解:依题意,与是关于3的平衡数;
则,
与是关于3的平衡数,
故答案为:,
(2)解:依题意,,
∵ ,
∴,
解得,
∴,
则
∴与是关于3的平衡数;
(3)解:∵,a和b是关于3的平衡数,
∴,
∴
,
∵,
∴,
∵m,n为整数,
∴
∴
,
故答案为:.
23.【解】(1)解:根据题意得,
,
则;
(2)解:∵四个全等的直角三角形,外围轮廓线的周长为80,
∴,
设,则,
由勾股定理可得,,
,
,
解得:,
∴,
∴该飞镖状图案的面积是;
(3)解:设每个三角形的面积都为y,
∴,,
∴,
又∵,
∴.
24.【解】(1)解:∵线段沿直线翻折得线段,
∴, ,
∴,
∵,
∴,
∴,
∴
,
故答案为:;
证明:∵线段沿直线翻折得线段,
∴,
∴,
∴,
∵,
∴,
即.
(2)解:
证明:连接,如图,
,,
∴,
由翻折知,,
由(1)知,,
,
,
,
∴,
∴,
∴.
(3)解:过点C作于H,如图,
由翻折知,,,
∴,
由(1)知:,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
由勾股定理,得,
∴,
∴,
由(2)知:,
∴,
∴,
∴.
25.【解】(1)解:,
,
,
,
,,
;
(2)证明:过点作交于点,交于点,如图所示:
,,
,
由(1)可知,,
平分,
,,
,
平分,,,
,
,
,,
平分;
(3)解:,
,
,
,,,
,
,
,
,
.
21世纪教育网(www.21cnjy.com)
八年级上册数学期中考试全真模拟试卷苏科版2025—2026学年
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.49的平方根为( )
A.7 B.-7 C.±7 D.±
2.以下是清华大学、北京大学、上海交通大学、中国人民大学四个大学的校徽,其中是轴对称图形的是( )
A.B. C. D.
3.我国是最早了解勾股定理的国家之一,它被记载于我国古代著名的数学著作《周髀算经》中,下列各组数中,是“勾股数”的是( )
A.1,1,2 B.1,,2 C.3,4,5 D.,,
4.下列条件不能判定△ABC是直角三角形的是( )
A. B.
C. D.
5.若,则的取值范围是( )
A. B. C. D.
6.下列运算正确的是( )
A.±5 B. C.2 D.4
7.数字中有理数的个数是( )
A.1 B.2 C.3 D.4
8.在的边上找一点P,使得.下面找法正确的是( )
A.B.C.D.
9.如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形与正方形,连结.若,,则的长为( )
A.2 B.3 C.4 D.
10.如图,在中,,D为延长线上一点,,垂足为C,,连接,若,则的面积为 ( )
A. B.9 C.18 D.36
二、填空题(6小题,每题3分,共18分)
11.已知等腰三角形的两条边长分别是2和4,则它的周长是 .
12.若一个正数的平方根是和,则这个正数是 .
13.化简: .
14.若直角三角形斜边上的高和中线长分别是4cm,5cm,则它的面积是 cm2.
15.如图,在中,为平分线,于,于,,,则 .
16.如图,,点、分别在边、上,且,,点、分别在边、上,则的最小值是 .
第II卷
八年级上册数学期中考试全真模拟试卷苏科版2025—2026学年
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1);
(2).
18.计算:
(1);
(2).
19.如图,点D、E在的边上,,求证:.
20.某数学兴趣小组用数学知识测一池塘两端之间的长度,他们所绘示意图如图所示,点B、F、C、E(其中点F、C为池塘的两端,之间的长度不能直接测量)在直线l上,点A,D在l的异侧,且,,测得.
(1)求证:;
(2)若,,求池塘两端F、C之间的长度.
21.如图,的顶点A、B、C都在小正方形的顶点上.
(1)画,使它与关于直线l对称;
(2)在直线l找一点P,使点P到点A、B的距离之和最短.
(3)在直线l找一点Q,使点Q到的距离相等.
22.若,则称x和y是关于3的平衡数.
(1)与_____是关于3的平衡数;与_____是关于3的平衡数;
(2)已知m为整数,若,请说明与是关于3的平衡数:
(3)已知,,m,n为整数,a和b是关于3的平衡数,则_____.
23.如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a.较短的直角边为b,斜边长为c,结合图①,试验证勾股定理;
(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓线的周长为80,,求该飞镖状图案的面积;
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形,正方形,正方形的面积分别为、、,若,求.
24.如图,中,,,过点任作一条直线,将线段沿直线翻折得线段,直线交直线于点,直线交直线于点.
(1)设,则______(用含m的代数式表示),并证明:;
(2)猜想线段、、之间的数量关系,并给出证明.
(3)若,,求的面积.
25.如图,在中,点在边上,,的平分线交于点,过点作,垂足为,且,连接.
(1)求的度数;
(2)求证:平分;
(3)若,,,且,求的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A B D D D D B
二、填空题
11.【解】解:当2为腰时,三边为2,2,4,由三角形三边关系定理可知,不能构成三角形,
当4为腰时,三边为4,4,2,符合三角形三边关系定理,周长为:4+4+2=10.
故答案为:10.
12.【解】解:根据题意得,,
解得,
,
∴这个正数是,
故答案为: 25.
13.【解】解:∵,
∴,
∴
∴.
故答案为:.
14.【解】解:由直角三角形斜边中线等于斜边的一半,可知斜边长为2×5=10cm,
所以它的面积是:×10×4=20(cm2);
故答案为:20
15.【解】解:
,
,
,
,,
,
为平分线,
,
于,
,,
设,则,,
,即,
解得:,
,
故答案为:.
16.【解】解:如图,作点关于的对称点,作点关于的对称点,连接,
由轴对称的性质得:,,,
∴,,
由两点之间线段最短可知,当点共线时,的值最小,最小值为,
即的最小值是,
故答案为:.
三、解答题
17.【解】(1)解:,
,
∴;
(2)解:,
,
,
∴.
18.【解】(1)解:
;
(2)解:
19.【解】证明:如图,过点A作C于P.
∵
∴;
∵,
∴,
∴,
∴.
20.【解】(1)证明:∵,
∴,
在与中,
,
;
(2)解:,
,
,
池塘两端F、C之间的长度是
21.【解】(1)解:如图,即为所求作.
(2)解:如图,点P即为所求作.
理由:根据(1)的结论,点A、点关于直线l成轴对称,
∴,
∴,
∴当点P在直线l和交点处时,,为最小值,
∴当点P在直线l和的交点处时,取最小值,
即点P到点A、点B的距离之和最短;
(3)解:如图,点Q即为所求作.
22.【解】(1)解:依题意,与是关于3的平衡数;
则,
与是关于3的平衡数,
故答案为:,
(2)解:依题意,,
∵ ,
∴,
解得,
∴,
则
∴与是关于3的平衡数;
(3)解:∵,a和b是关于3的平衡数,
∴,
∴
,
∵,
∴,
∵m,n为整数,
∴
∴
,
故答案为:.
23.【解】(1)解:根据题意得,
,
则;
(2)解:∵四个全等的直角三角形,外围轮廓线的周长为80,
∴,
设,则,
由勾股定理可得,,
,
,
解得:,
∴,
∴该飞镖状图案的面积是;
(3)解:设每个三角形的面积都为y,
∴,,
∴,
又∵,
∴.
24.【解】(1)解:∵线段沿直线翻折得线段,
∴, ,
∴,
∵,
∴,
∴,
∴
,
故答案为:;
证明:∵线段沿直线翻折得线段,
∴,
∴,
∴,
∵,
∴,
即.
(2)解:
证明:连接,如图,
,,
∴,
由翻折知,,
由(1)知,,
,
,
,
∴,
∴,
∴.
(3)解:过点C作于H,如图,
由翻折知,,,
∴,
由(1)知:,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
由勾股定理,得,
∴,
∴,
由(2)知:,
∴,
∴,
∴.
25.【解】(1)解:,
,
,
,
,,
;
(2)证明:过点作交于点,交于点,如图所示:
,,
,
由(1)可知,,
平分,
,,
,
平分,,,
,
,
,,
平分;
(3)解:,
,
,
,,,
,
,
,
,
.
21世纪教育网(www.21cnjy.com)
同课章节目录
