第四章一次函数小结与复习 课件(共26张PPT) 2025-2026学年度北师版数学八年级上册
文档属性
| 名称 | 第四章一次函数小结与复习 课件(共26张PPT) 2025-2026学年度北师版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 413.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 05:57:33 | ||
图片预览







文档简介
(共26张PPT)
小结与复习
第四章 一次函数
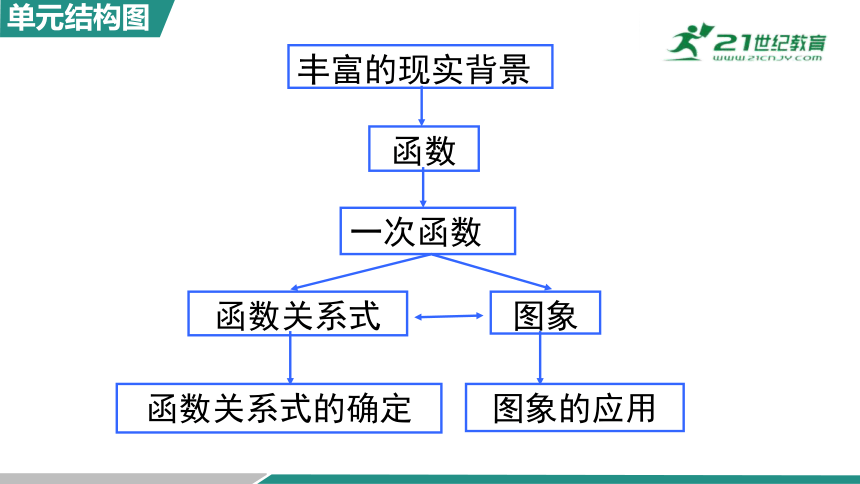
丰富的现实背景
函数
一次函数
函数关系式
图象
函数关系式的确定
图象的应用
1. 叫变量.
2.函数定义:
数值发生变化的量
在一个变化过程中,如果有两个变量 x 与 y,并且对于变量 x 的每一个确定的值,变量 y 都有唯一确定的值与它对应,那么我们称 y 是 x 的函数,其中 x 是自变量.
一、函数
(所用方法:描点法)
3.函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
关系式法
图象法
5.函数的三种表示方法:
4.描点法画图象的步骤:列表、描点、连线
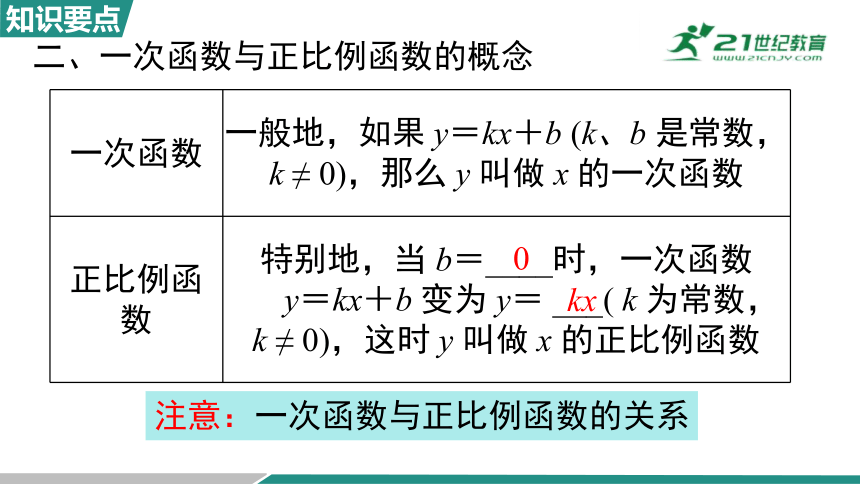
一次函数 一般地,如果 y=kx+b (k、b 是常数,k ≠ 0),那么 y 叫做 x 的一次函数
正比例函数 特别地,当 b=____时,一次函数
y=kx+b 变为 y= ___( k 为常数,k ≠ 0),这时 y 叫做 x 的正比例函数
注意:一次函数与正比例函数的关系
0
kx
二、一次函数与正比例函数的概念
函数 字母取值 ( k>0 ) 图象 经过的象限 函数性质
y=kx + b (k ≠ 0) b>0 y 随 x增大而
增大
b=0 b<0 一、三象限
一、二、三象限
一、三、四象限
三、一次函数的图象与性质
函数 字母取值 ( k<0 ) 图象 经过的象限 函数性质
y=kx + b (k ≠ 0) b>0 ________ y 随 x增大而
减小
b=0 ________ b<0 ________ 一、二、四象限
二、四象限
二、三、四象限
求一次函数关系式一般步骤:
(1)先设出函数关系式;
(2)根据条件列关于待定系数的方程;
(3)解方程求出关系式中未知的系数;
(4)把求出的系数代入设的关系式,从而具体写出这个关系式.
四、求一次函数的关系式
其中过原点的直线是_____;函数 y 随 x 的增大而增大的是___________;函数 y 随 x 的增大而减小的是______;图象在第一、二、三象限的是_____.
考点一 一次函数的图象与性质
例1 填空题:
②
①、②、③
④
③
有下列函数:① , ② ,
③ , ④ .
x
y
2
=
例2 已知函数 y = (2m + 1)x + m﹣3;
(1)若该函数是正比例函数,求 m 的值;
(2)若函数的图象平行直线 y = 3x﹣3,求 m 的值;
(3)若这个函数是一次函数,且 y 随着 x 的增大而减小,
求 m 的取值范围;
(4)若这个函数图象过点 (1,4),求这个函数的解析式.
【分析】(1)由函数是正比例函数得m-3=0且2m+1≠0;(2)由两直线平行得2m+1=3;(3)一次函数中 y 随着 x 的增大而减小,即2m+1<0;(4)代入该点坐标即可求解.
考点一 一次函数的图象与性质
解:(1) ∵函数是正比例函数,
∴m﹣3 = 0,且 2m + 1≠ 0,解得 m = 3.
(2) ∵ 函数的图象平行于直线 y = 3x﹣3,
∴ 2m + 1 = 3,解得 m = 1.
(3) ∵ y 随着 x 的增大而减小,
∴ 2m + 1<0,解得 m< .
(4)∵ 该函数图象过点 (1,4),代入得 2m + 1 + m - 3 = 4,
解得 m = 2,∴该函数的解析式为 y = 5x - 1.
考点一 一次函数的图象与性质
一次函数的图象与 y 轴交点的纵坐标就是 y = kx + b 中 b 的值;两条直线平行,其函数解析式中的自变量系数 k 相等;当 k>0 时,y 随 x 的增大而增大;当 k<0 时,y 随 x 的增大而减小.
总结
考点一 一次函数的图象与性质
1.函数 的图象与 x 轴交点的坐标为_______,
与 y 轴的交点坐标为______.
(-6,0)
(0,4)
2.已知函数 y = -x + 2 当 -1<x≤1 时,y 的取值范围是_______.
1≤y<3
【针对训练】
考点一 一次函数的图象与性质
3. 已知一次函数 y = kx + b,y 随着 x 的增大而减小,且 kb<0,则在直角坐标系内它的大致图象是( )
A B C D
A
x
y
O
O
x
y
x
y
y
x
O
O
考点一 一次函数的图象与性质
4. 一次函数 y = ax + b 与 y = ax + c (a>0) 在同一坐标系中的图象可能是( )
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
A
考点一 一次函数的图象与性质
例3 已知一次函数的图象经过 A (2,4),B (0,2) 两点,
求:
(1) 一次函数的表达式;
解:(1) 设一次函数的表达式为 y=kx+b (k≠0).
因为图象经过 A (2,4),B (0,2) 两点,
代入表达式中得
考点二 一次函数的图象与性质
2k + b = 4, b = 2,
解得 k = 1,b = 2.
因此这个一次函数的表达式为 y = x + 2.
(2) 求此函数图象与两坐标轴围成的三角形的面积 S.
解:(2) 因为一次函数 y=x+2 的图象与 x 轴、y 轴的交点坐标分别为 (-2,0) 和 (0,2) ,
考点二 一次函数的图象与性质
【针对训练】5. 如图,在平面直角坐标系中,已知直线 y=kx+3 与 x 轴相交于点 A(2,0),与 y 轴交于点 B.
(1) 求 k 的值及 △AOB 的面积;
解:(1) 把 A(2,0) 代入 y=kx+3,
得 2k+3=0,
所以 B(0,3).
当 x = 0 时,y = 3.
考点二 一次函数的图象与性质
(2) 点 C 在 x 轴上,若△ABC 是以 AB 为腰的等腰三角形,求点 C 的坐标.
解:(2) 设 C(m,0).
因为 A(2,0),B(0,3),
所以 AC2=(m-2)2,BC2=m2+9,
AB2=13.
①若 AB,AC 为腰,则 AC2=AB2,
所以 (m-2)2=13,
考点二 一次函数的图象与性质
②若 AB,BC 为腰,则 BC2=AB2,
所以 m2+9=13,
解得 m=2 (与点 A 重合,舍去)
或m=-2.
∴C(-2,0).
综上所述,△ABC 是以 AB 为腰的等腰三角形时,点 C 的坐标为(-2,0).
考点二 一次函数的图象与性质
例4 李老师开车从甲地到相距 240 千米的乙地,如果油箱剩余油量 y (升) 与行驶里程 x (千米) 之间是一次函数关系,其图象如图所示,那么
到达乙地时油箱剩余油量是多少升?
考点三 一次函数的图象与性质
解:设一次函数的关系式为 y=kx+35,
将(160,25)代入,得 160k+35=25,
解得 k= ,
所以一次函数的关系式为 y= x+35.
再将 x=240 代入 y= x+35,
得 y= ×240+35=20,
即到达乙地时油箱剩余油量是 20 升.
考点三 一次函数的图象与性质
【针对训练】6. 自来水公司有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池,甲、乙两个蓄水池中水的深度 y (米) 与注水时间 x (时) 之间的函数图象如图所示,结合图象回答下列问题.
(1) 分别求出甲、乙两个蓄水池中
水的深度 y 与注水时间 x 之间的
函数关系式;
考点三 一次函数的图象与性质
解:(1)设它们的函数关系式为
y=kx+b,根据甲的函数图象可知,
当 x=0,y=2;当 x=3时,y=0,
将它们代入关系式 y=kx+b 中,
得 k= ,b=2,
所以甲蓄水池中水的深度 y 与注水时间 x 之间的函数关系式为:y= x+2. 同理可得乙蓄水池中水的深度 y 与注水时间 x 之间的函数关系式为:y=x+1.
(1)分别求出甲、乙两个蓄水池中水的深度 y 与注水时间 x 之间的函数关系式;
(2)求注入多长时间后甲、乙两个蓄水池的深度相同;
(2) 由题意得 x+2=x+1,
解得 x= .
故当注水 小时后,甲、乙两个蓄水池水的深度相同;
(3) 求注入多长时间甲、乙两个蓄水池的蓄水量相同?
(3) 从函数图象判断当甲水池的水全部注入乙水池后,甲水池深度下降 2 米,而乙水池深度上升 3 米,所以甲乙水池的底面积之比为 S甲 : S乙 = 3 : 2,
S甲·( x+2) = S乙·(x+1),解得 x = 1.故注水 1 小时后,甲乙两蓄水池的蓄水量相同.
小结与复习
第四章 一次函数
丰富的现实背景
函数
一次函数
函数关系式
图象
函数关系式的确定
图象的应用
1. 叫变量.
2.函数定义:
数值发生变化的量
在一个变化过程中,如果有两个变量 x 与 y,并且对于变量 x 的每一个确定的值,变量 y 都有唯一确定的值与它对应,那么我们称 y 是 x 的函数,其中 x 是自变量.
一、函数
(所用方法:描点法)
3.函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
关系式法
图象法
5.函数的三种表示方法:
4.描点法画图象的步骤:列表、描点、连线
一次函数 一般地,如果 y=kx+b (k、b 是常数,k ≠ 0),那么 y 叫做 x 的一次函数
正比例函数 特别地,当 b=____时,一次函数
y=kx+b 变为 y= ___( k 为常数,k ≠ 0),这时 y 叫做 x 的正比例函数
注意:一次函数与正比例函数的关系
0
kx
二、一次函数与正比例函数的概念
函数 字母取值 ( k>0 ) 图象 经过的象限 函数性质
y=kx + b (k ≠ 0) b>0 y 随 x增大而
增大
b=0 b<0 一、三象限
一、二、三象限
一、三、四象限
三、一次函数的图象与性质
函数 字母取值 ( k<0 ) 图象 经过的象限 函数性质
y=kx + b (k ≠ 0) b>0 ________ y 随 x增大而
减小
b=0 ________ b<0 ________ 一、二、四象限
二、四象限
二、三、四象限
求一次函数关系式一般步骤:
(1)先设出函数关系式;
(2)根据条件列关于待定系数的方程;
(3)解方程求出关系式中未知的系数;
(4)把求出的系数代入设的关系式,从而具体写出这个关系式.
四、求一次函数的关系式
其中过原点的直线是_____;函数 y 随 x 的增大而增大的是___________;函数 y 随 x 的增大而减小的是______;图象在第一、二、三象限的是_____.
考点一 一次函数的图象与性质
例1 填空题:
②
①、②、③
④
③
有下列函数:① , ② ,
③ , ④ .
x
y
2
=
例2 已知函数 y = (2m + 1)x + m﹣3;
(1)若该函数是正比例函数,求 m 的值;
(2)若函数的图象平行直线 y = 3x﹣3,求 m 的值;
(3)若这个函数是一次函数,且 y 随着 x 的增大而减小,
求 m 的取值范围;
(4)若这个函数图象过点 (1,4),求这个函数的解析式.
【分析】(1)由函数是正比例函数得m-3=0且2m+1≠0;(2)由两直线平行得2m+1=3;(3)一次函数中 y 随着 x 的增大而减小,即2m+1<0;(4)代入该点坐标即可求解.
考点一 一次函数的图象与性质
解:(1) ∵函数是正比例函数,
∴m﹣3 = 0,且 2m + 1≠ 0,解得 m = 3.
(2) ∵ 函数的图象平行于直线 y = 3x﹣3,
∴ 2m + 1 = 3,解得 m = 1.
(3) ∵ y 随着 x 的增大而减小,
∴ 2m + 1<0,解得 m< .
(4)∵ 该函数图象过点 (1,4),代入得 2m + 1 + m - 3 = 4,
解得 m = 2,∴该函数的解析式为 y = 5x - 1.
考点一 一次函数的图象与性质
一次函数的图象与 y 轴交点的纵坐标就是 y = kx + b 中 b 的值;两条直线平行,其函数解析式中的自变量系数 k 相等;当 k>0 时,y 随 x 的增大而增大;当 k<0 时,y 随 x 的增大而减小.
总结
考点一 一次函数的图象与性质
1.函数 的图象与 x 轴交点的坐标为_______,
与 y 轴的交点坐标为______.
(-6,0)
(0,4)
2.已知函数 y = -x + 2 当 -1<x≤1 时,y 的取值范围是_______.
1≤y<3
【针对训练】
考点一 一次函数的图象与性质
3. 已知一次函数 y = kx + b,y 随着 x 的增大而减小,且 kb<0,则在直角坐标系内它的大致图象是( )
A B C D
A
x
y
O
O
x
y
x
y
y
x
O
O
考点一 一次函数的图象与性质
4. 一次函数 y = ax + b 与 y = ax + c (a>0) 在同一坐标系中的图象可能是( )
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
A
考点一 一次函数的图象与性质
例3 已知一次函数的图象经过 A (2,4),B (0,2) 两点,
求:
(1) 一次函数的表达式;
解:(1) 设一次函数的表达式为 y=kx+b (k≠0).
因为图象经过 A (2,4),B (0,2) 两点,
代入表达式中得
考点二 一次函数的图象与性质
2k + b = 4, b = 2,
解得 k = 1,b = 2.
因此这个一次函数的表达式为 y = x + 2.
(2) 求此函数图象与两坐标轴围成的三角形的面积 S.
解:(2) 因为一次函数 y=x+2 的图象与 x 轴、y 轴的交点坐标分别为 (-2,0) 和 (0,2) ,
考点二 一次函数的图象与性质
【针对训练】5. 如图,在平面直角坐标系中,已知直线 y=kx+3 与 x 轴相交于点 A(2,0),与 y 轴交于点 B.
(1) 求 k 的值及 △AOB 的面积;
解:(1) 把 A(2,0) 代入 y=kx+3,
得 2k+3=0,
所以 B(0,3).
当 x = 0 时,y = 3.
考点二 一次函数的图象与性质
(2) 点 C 在 x 轴上,若△ABC 是以 AB 为腰的等腰三角形,求点 C 的坐标.
解:(2) 设 C(m,0).
因为 A(2,0),B(0,3),
所以 AC2=(m-2)2,BC2=m2+9,
AB2=13.
①若 AB,AC 为腰,则 AC2=AB2,
所以 (m-2)2=13,
考点二 一次函数的图象与性质
②若 AB,BC 为腰,则 BC2=AB2,
所以 m2+9=13,
解得 m=2 (与点 A 重合,舍去)
或m=-2.
∴C(-2,0).
综上所述,△ABC 是以 AB 为腰的等腰三角形时,点 C 的坐标为(-2,0).
考点二 一次函数的图象与性质
例4 李老师开车从甲地到相距 240 千米的乙地,如果油箱剩余油量 y (升) 与行驶里程 x (千米) 之间是一次函数关系,其图象如图所示,那么
到达乙地时油箱剩余油量是多少升?
考点三 一次函数的图象与性质
解:设一次函数的关系式为 y=kx+35,
将(160,25)代入,得 160k+35=25,
解得 k= ,
所以一次函数的关系式为 y= x+35.
再将 x=240 代入 y= x+35,
得 y= ×240+35=20,
即到达乙地时油箱剩余油量是 20 升.
考点三 一次函数的图象与性质
【针对训练】6. 自来水公司有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池,甲、乙两个蓄水池中水的深度 y (米) 与注水时间 x (时) 之间的函数图象如图所示,结合图象回答下列问题.
(1) 分别求出甲、乙两个蓄水池中
水的深度 y 与注水时间 x 之间的
函数关系式;
考点三 一次函数的图象与性质
解:(1)设它们的函数关系式为
y=kx+b,根据甲的函数图象可知,
当 x=0,y=2;当 x=3时,y=0,
将它们代入关系式 y=kx+b 中,
得 k= ,b=2,
所以甲蓄水池中水的深度 y 与注水时间 x 之间的函数关系式为:y= x+2. 同理可得乙蓄水池中水的深度 y 与注水时间 x 之间的函数关系式为:y=x+1.
(1)分别求出甲、乙两个蓄水池中水的深度 y 与注水时间 x 之间的函数关系式;
(2)求注入多长时间后甲、乙两个蓄水池的深度相同;
(2) 由题意得 x+2=x+1,
解得 x= .
故当注水 小时后,甲、乙两个蓄水池水的深度相同;
(3) 求注入多长时间甲、乙两个蓄水池的蓄水量相同?
(3) 从函数图象判断当甲水池的水全部注入乙水池后,甲水池深度下降 2 米,而乙水池深度上升 3 米,所以甲乙水池的底面积之比为 S甲 : S乙 = 3 : 2,
S甲·( x+2) = S乙·(x+1),解得 x = 1.故注水 1 小时后,甲乙两蓄水池的蓄水量相同.
同课章节目录
