八年级上册数学第一次月考全真模拟试卷(含答案)苏科版2025—2026学年
文档属性
| 名称 | 八年级上册数学第一次月考全真模拟试卷(含答案)苏科版2025—2026学年 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 15:52:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级上册数学第一次月考全真模拟试卷苏科版2025—2026学年
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下列我国四大银行的商标图案中,不是轴对称图形的是( )
A. B. C. D.
2.下列条件中,不能判定的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.若两个图形关于某条直线对称,则这两个图形全等
B.等腰三角形一边上的中线和这条边上的高重合
C.面积相等的两个图形是全等形
D.周长相等的两个三角形全等
4.数学课上,同学们用纸片进行折纸操作.按照下列各图所示的折叠过程,线段是中线的是( )
A.B.C. D.
5.三角形中到三条边距离相等的点是( )
A.三条边的垂直平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条角平分线的交点
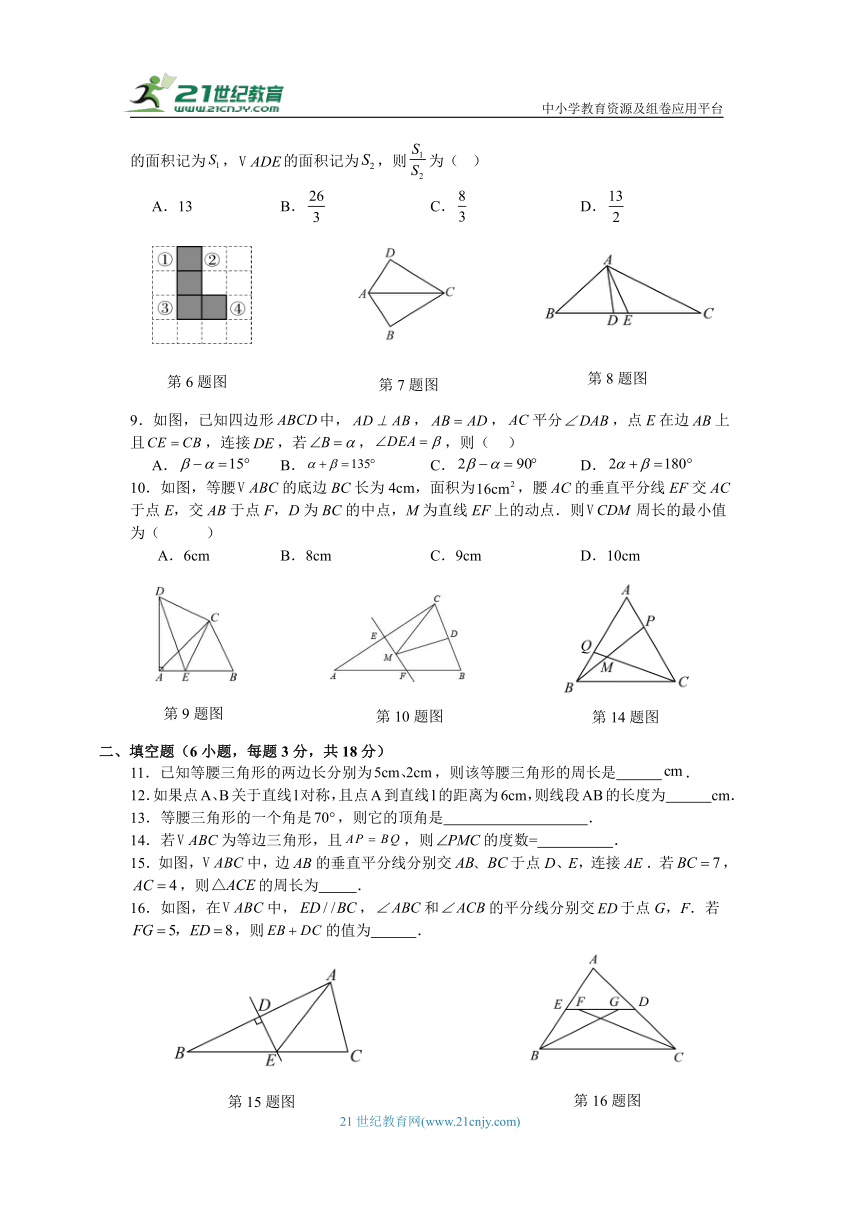
6.如图,在正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( )
A.① B.② C.③ D.④
7.如图,已知,那么添加下列一个条件后,仍然不能判定的是( )
A. B.
C. D.
8.如图,在中,,,为中点,为的角平分线,的面积记为,的面积记为,则为( )
A.13 B. C. D.
9.如图,已知四边形中,,,平分,点E在边上且,连接,若,,则( )
A. B. C. D.
10.如图,等腰的底边BC长为4cm,面积为,腰AC的垂直平分线EF交AC于点E,交AB于点F,D为BC的中点,M为直线EF上的动点.则周长的最小值为( )
A.6cm B.8cm C.9cm D.10cm
二、填空题(6小题,每题3分,共18分)
11.已知等腰三角形的两边长分别为,则该等腰三角形的周长是 .
12.如果点A、B关于直线l对称,且点A到直线l的距离为6cm,则线段AB的长度为 cm.
13.等腰三角形的一个角是,则它的顶角是 .
14.若为等边三角形,且,则的度数= .
15.如图,中,边的垂直平分线分别交于点D、E,连接.若,,则的周长为 .
16.如图,在中,,和的平分线分别交于点G,F.若,则的值为 .
第II卷
八年级上册数学第一次月考全真模拟试卷苏科版2025—2026学年
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
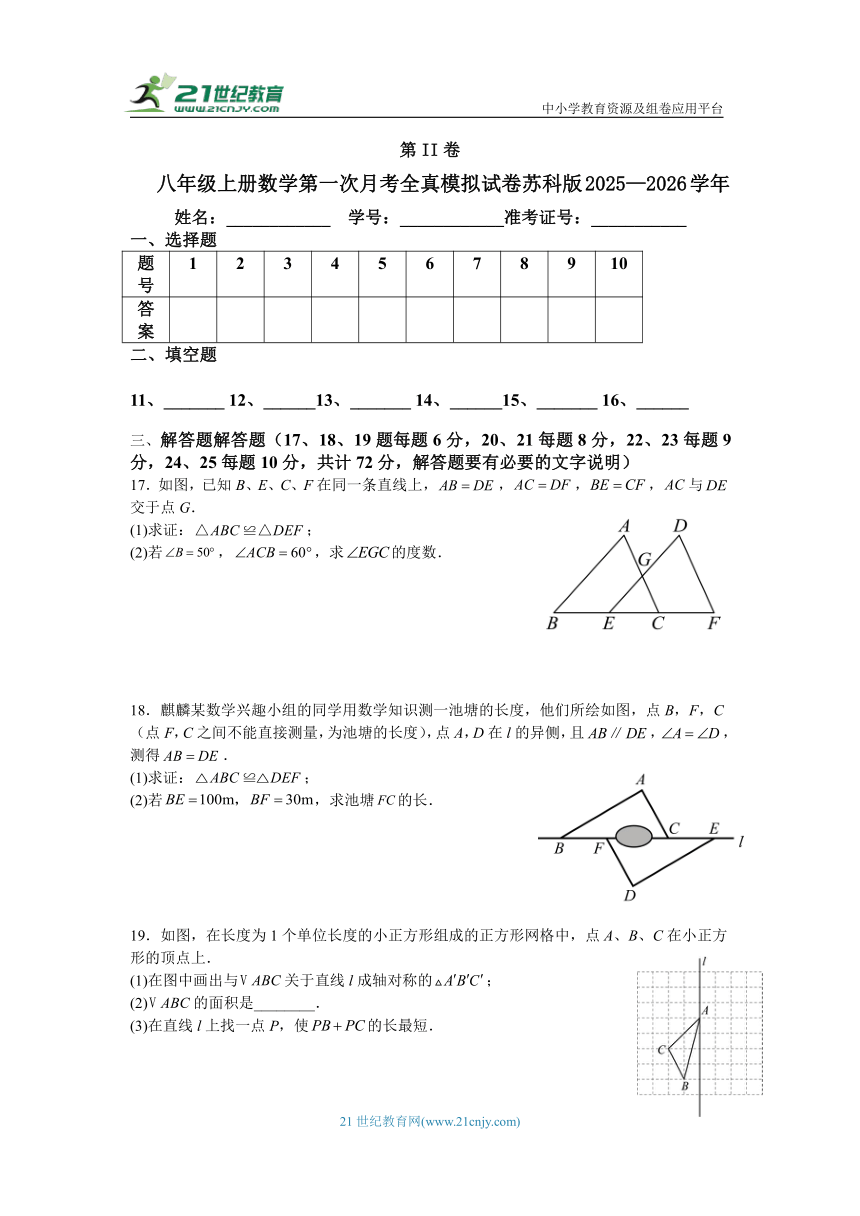
17.如图,已知B、E、C、F在同一条直线上,,,,与交于点G.
(1)求证:;
(2)若,,求的度数.
18.麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B,F,C(点F,C之间不能直接测量,为池塘的长度),点A,D在l的异侧,且,,测得.
(1)求证:;
(2)若,求池塘的长.
19.如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线l成轴对称的;
(2)的面积是________.
(3)在直线l上找一点P,使的长最短.
20.如图,在中,,的垂直平分线交于点,交于点.
(1)若,求的度数;
(2)若,的周长为,求的长.
21.如图,已知在四边形中,于B,于C,平分,且E为的中点.
(1)求证:平分;
(2)求的度数.
22.如图,在中,垂直平分边,交BC于点E,平分的外角,,垂足为点G,,垂足为点H.
(1)求证:;
(2)如果,求证:点E在的垂直平分线上.
23.如图,中,,D是延长线上一点,点E是的平分线上一点,过点E作于F,于G.
(1)求证:;
(2)若,,,求的长.
24.如图,在中,,,为直线上一动点,连接.在直线的右侧作,且.
观察发现:
(1)如图①,当点在线段上时,过点作的垂线,垂足为,判断线段与之间的关系,并说明理由;
探究迁移:
(2)将如图①中的,连接,交直线于点,我们很容易发现.如图②,当点在线段的延长线上时,连接交直线于点,线段和线段之间的关系有没有变化?此时吗?说说理由.
拓展应用:
(3)如图③,当点在线段的延长线上时,当,时,求和的面积.
25.如图,在中,为高线,.点为上一点,,连接,交于点,若.
(1)猜想线段与的位置关系,并证明;
(2)若动点从点出发沿射线以每秒6个单位长度的速度运动,运动的时间为秒.
①当点在线段上时,是否存在的值,使得的面积为27?若存在,请求出的值;若不存在,请说明理由;
②动点从点出发沿线段以每秒2个单位长度的速度向终点运动,,两点同时出发,当点到达点时,,两点同时停止运动.设运动时间为秒,点是直线上一点,且,当与全等时,请直接写出的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A C D A D B B D
二、填空题
11.【解】解:由等腰三角形性质,分两种情况:
当腰是时,三角形的边长为,则该等腰三角形的周长是;
当腰是时,边长为,则由构成三角形的三边关系可知三条边长不能构成三角形,此种情况不存在;
故答案为:12.
12.【解】试题分析:根据轴对称的性质得到A到直线l的距离与B到直线l的距离相等.
试题解析:线段AB的长度=6+6=12cm.
考点:轴对称的性质.
13.【解】解:①当角为顶角时,顶角度数为;
②当为底角时,顶角:,
故答案为:或.
14.【解】解:∵为等边三角形,
∴,
∵,
∴,
∴,
∴,
故答案为:
15.【解】解:是的垂直平分线,
,
的周长,
故答案为:11.
16.【解】∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
故答案为:13.
三、解答题
17.【解】(1)证明:∵,
∴,即,
在和中,
,
∴;
(2)解:如图:
∵,
∴,
∴.
18.【解】(1)证明:∵,
∴,
在与中,
∴;
(2)解:∵
∴
∴,
∴,
∵
∴m.
答:的长是40m
19.【解】(1)解:如图,即为所求.
(2)解:
(3)解:如图,点即为所求.
20.【解】(1)解:∵,,
∴ ,
∵是的垂直平分线,
∴,
∴,
∴;
(2)解:∵是的垂直平分线,,
∴,,
∴的周长为:,
∴.
21.【解】(1)证明:如图,过点E作于F,
∵,平分,
∴,
∵E是的中点,
∴,
∴,
又∵,,
∴平分;
(2)∵,
∴,
∴,
∴,
∵平分,平分,
∴,,
∴,
∴.
22.【解】(1)∵垂直平分,
∴.
∵平分的外角,,
∴.
在中,
,
∴;
(2)连接,
由(1)可得.
∵,
∴,
∴.
由题意可得点E是的中点,
∴,
∴,
∴点E在的垂直平分线上.
23.【解】(1)证明:∵平分,
∴.
又∵,,
∴.
在和中:
,,,
∴.
(2)解:∵平分且,,
∴.
∵
∴,
∵
∴
∴
即
在和中
,,
∴.
∴.
又∵,,
即,
又∵,
∴.
∴.
∴.
24.【解】(1)结论:,,理由如下,
根据题意可知,,
∴,
∴,
∵,
∴,
∴,
∴.
∵和,
,
∴,
∴,
∵,
∴,
故线段与之间的关系为:且;
(2)结论:线段与之间的关系不变,,理由如下:
从图②可知,,,
∴,
同理可得,,,
∴,
∵,
∴,
在和中,
,
∴,
∴,
故本题结论为:与之间的关系不变,;
(3)如图③,当点在线段的延长线上时,
同理可得,,,
∴,,,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,
则根据图形面积割补法可得:
,
∴,
∴和的面积分别为24和88.
25.【解】(1)解:,理由如下:
在中,为高,
,
又,
,
,,
,
;
(2)解:①存在的值,使得的面积为27,理由如下:
,,
,
,
,,
由(1)可知,,
,
在线段上,
,
解得:;
②,
,
、当点在线段延长线上时,如图3,
,
,
,
当时,,
此时,,
解得:;
、当点在线段上时,如图4,
,
,
,
当时,,
此时,,
解得:;
综上所述,当与全等时,的值为或.
21世纪教育网(www.21cnjy.com)
八年级上册数学第一次月考全真模拟试卷苏科版2025—2026学年
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下列我国四大银行的商标图案中,不是轴对称图形的是( )
A. B. C. D.
2.下列条件中,不能判定的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.若两个图形关于某条直线对称,则这两个图形全等
B.等腰三角形一边上的中线和这条边上的高重合
C.面积相等的两个图形是全等形
D.周长相等的两个三角形全等
4.数学课上,同学们用纸片进行折纸操作.按照下列各图所示的折叠过程,线段是中线的是( )
A.B.C. D.
5.三角形中到三条边距离相等的点是( )
A.三条边的垂直平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条角平分线的交点
6.如图,在正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( )
A.① B.② C.③ D.④
7.如图,已知,那么添加下列一个条件后,仍然不能判定的是( )
A. B.
C. D.
8.如图,在中,,,为中点,为的角平分线,的面积记为,的面积记为,则为( )
A.13 B. C. D.
9.如图,已知四边形中,,,平分,点E在边上且,连接,若,,则( )
A. B. C. D.
10.如图,等腰的底边BC长为4cm,面积为,腰AC的垂直平分线EF交AC于点E,交AB于点F,D为BC的中点,M为直线EF上的动点.则周长的最小值为( )
A.6cm B.8cm C.9cm D.10cm
二、填空题(6小题,每题3分,共18分)
11.已知等腰三角形的两边长分别为,则该等腰三角形的周长是 .
12.如果点A、B关于直线l对称,且点A到直线l的距离为6cm,则线段AB的长度为 cm.
13.等腰三角形的一个角是,则它的顶角是 .
14.若为等边三角形,且,则的度数= .
15.如图,中,边的垂直平分线分别交于点D、E,连接.若,,则的周长为 .
16.如图,在中,,和的平分线分别交于点G,F.若,则的值为 .
第II卷
八年级上册数学第一次月考全真模拟试卷苏科版2025—2026学年
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.如图,已知B、E、C、F在同一条直线上,,,,与交于点G.
(1)求证:;
(2)若,,求的度数.
18.麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B,F,C(点F,C之间不能直接测量,为池塘的长度),点A,D在l的异侧,且,,测得.
(1)求证:;
(2)若,求池塘的长.
19.如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线l成轴对称的;
(2)的面积是________.
(3)在直线l上找一点P,使的长最短.
20.如图,在中,,的垂直平分线交于点,交于点.
(1)若,求的度数;
(2)若,的周长为,求的长.
21.如图,已知在四边形中,于B,于C,平分,且E为的中点.
(1)求证:平分;
(2)求的度数.
22.如图,在中,垂直平分边,交BC于点E,平分的外角,,垂足为点G,,垂足为点H.
(1)求证:;
(2)如果,求证:点E在的垂直平分线上.
23.如图,中,,D是延长线上一点,点E是的平分线上一点,过点E作于F,于G.
(1)求证:;
(2)若,,,求的长.
24.如图,在中,,,为直线上一动点,连接.在直线的右侧作,且.
观察发现:
(1)如图①,当点在线段上时,过点作的垂线,垂足为,判断线段与之间的关系,并说明理由;
探究迁移:
(2)将如图①中的,连接,交直线于点,我们很容易发现.如图②,当点在线段的延长线上时,连接交直线于点,线段和线段之间的关系有没有变化?此时吗?说说理由.
拓展应用:
(3)如图③,当点在线段的延长线上时,当,时,求和的面积.
25.如图,在中,为高线,.点为上一点,,连接,交于点,若.
(1)猜想线段与的位置关系,并证明;
(2)若动点从点出发沿射线以每秒6个单位长度的速度运动,运动的时间为秒.
①当点在线段上时,是否存在的值,使得的面积为27?若存在,请求出的值;若不存在,请说明理由;
②动点从点出发沿线段以每秒2个单位长度的速度向终点运动,,两点同时出发,当点到达点时,,两点同时停止运动.设运动时间为秒,点是直线上一点,且,当与全等时,请直接写出的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A C D A D B B D
二、填空题
11.【解】解:由等腰三角形性质,分两种情况:
当腰是时,三角形的边长为,则该等腰三角形的周长是;
当腰是时,边长为,则由构成三角形的三边关系可知三条边长不能构成三角形,此种情况不存在;
故答案为:12.
12.【解】试题分析:根据轴对称的性质得到A到直线l的距离与B到直线l的距离相等.
试题解析:线段AB的长度=6+6=12cm.
考点:轴对称的性质.
13.【解】解:①当角为顶角时,顶角度数为;
②当为底角时,顶角:,
故答案为:或.
14.【解】解:∵为等边三角形,
∴,
∵,
∴,
∴,
∴,
故答案为:
15.【解】解:是的垂直平分线,
,
的周长,
故答案为:11.
16.【解】∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
故答案为:13.
三、解答题
17.【解】(1)证明:∵,
∴,即,
在和中,
,
∴;
(2)解:如图:
∵,
∴,
∴.
18.【解】(1)证明:∵,
∴,
在与中,
∴;
(2)解:∵
∴
∴,
∴,
∵
∴m.
答:的长是40m
19.【解】(1)解:如图,即为所求.
(2)解:
(3)解:如图,点即为所求.
20.【解】(1)解:∵,,
∴ ,
∵是的垂直平分线,
∴,
∴,
∴;
(2)解:∵是的垂直平分线,,
∴,,
∴的周长为:,
∴.
21.【解】(1)证明:如图,过点E作于F,
∵,平分,
∴,
∵E是的中点,
∴,
∴,
又∵,,
∴平分;
(2)∵,
∴,
∴,
∴,
∵平分,平分,
∴,,
∴,
∴.
22.【解】(1)∵垂直平分,
∴.
∵平分的外角,,
∴.
在中,
,
∴;
(2)连接,
由(1)可得.
∵,
∴,
∴.
由题意可得点E是的中点,
∴,
∴,
∴点E在的垂直平分线上.
23.【解】(1)证明:∵平分,
∴.
又∵,,
∴.
在和中:
,,,
∴.
(2)解:∵平分且,,
∴.
∵
∴,
∵
∴
∴
即
在和中
,,
∴.
∴.
又∵,,
即,
又∵,
∴.
∴.
∴.
24.【解】(1)结论:,,理由如下,
根据题意可知,,
∴,
∴,
∵,
∴,
∴,
∴.
∵和,
,
∴,
∴,
∵,
∴,
故线段与之间的关系为:且;
(2)结论:线段与之间的关系不变,,理由如下:
从图②可知,,,
∴,
同理可得,,,
∴,
∵,
∴,
在和中,
,
∴,
∴,
故本题结论为:与之间的关系不变,;
(3)如图③,当点在线段的延长线上时,
同理可得,,,
∴,,,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,
则根据图形面积割补法可得:
,
∴,
∴和的面积分别为24和88.
25.【解】(1)解:,理由如下:
在中,为高,
,
又,
,
,,
,
;
(2)解:①存在的值,使得的面积为27,理由如下:
,,
,
,
,,
由(1)可知,,
,
在线段上,
,
解得:;
②,
,
、当点在线段延长线上时,如图3,
,
,
,
当时,,
此时,,
解得:;
、当点在线段上时,如图4,
,
,
,
当时,,
此时,,
解得:;
综上所述,当与全等时,的值为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
