第五章走进几何世界单元测试卷(含答案)苏科版2025—2026学年七年级上册
文档属性
| 名称 | 第五章走进几何世界单元测试卷(含答案)苏科版2025—2026学年七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 591.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 20:31:03 | ||
图片预览

文档简介
第五章走进几何世界单元测试卷苏科版2025—2026学年七年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
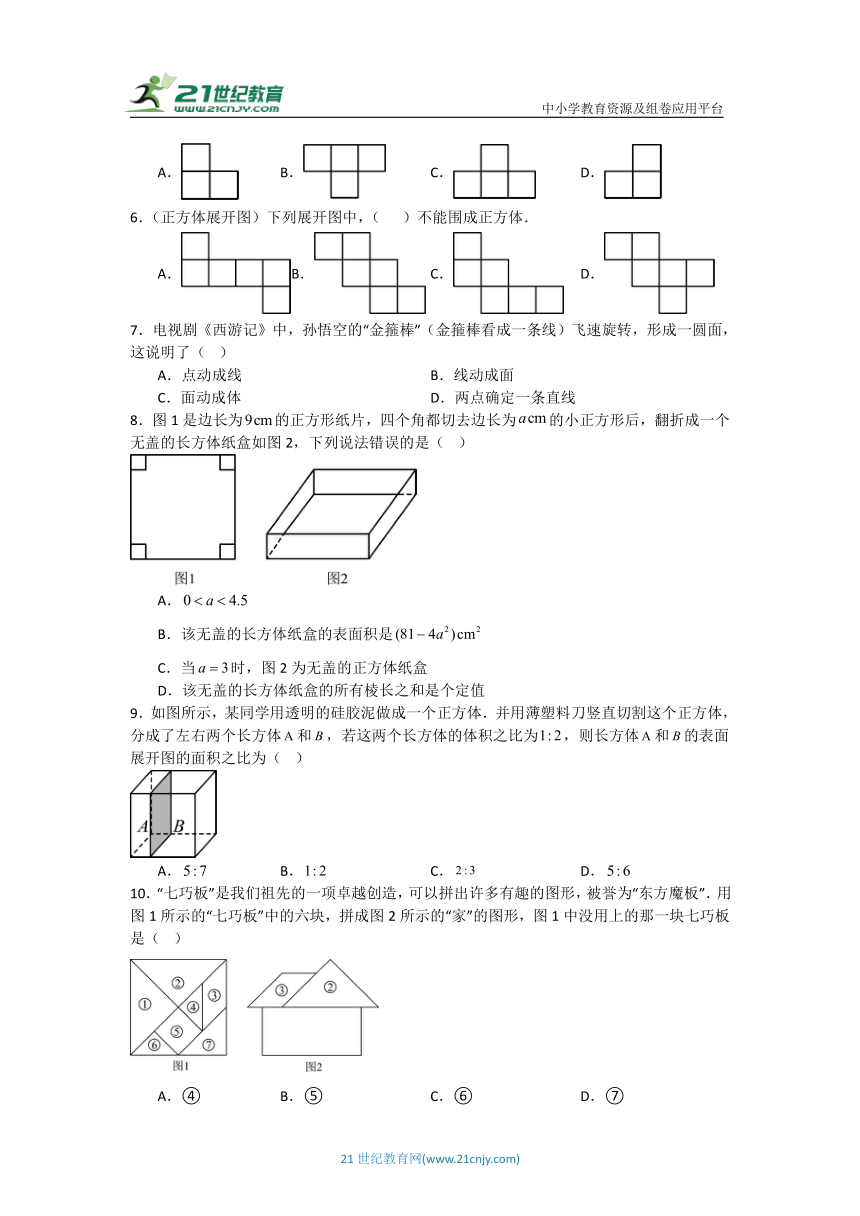
1.下面图形经过折叠不能围成棱柱的是( )
A. B. C. D.
2.下列图形中,为三棱柱的侧面展开图的是( )
A. B. C. D.
3.将如图所示的直角三角形绕直线l旋转一周,得到的立体图形是( )
A. B. C. D.
4.如图是一个正方体展开图,图中的六个正方形内分别标有:有、志、者、事、竟、成,将其围成一个正方体后,则与“成”相对的是( )
A.竞 B.有 C.事 D.者
5.一个由5个相同的小正方体组成的立体图形如图所示,则从正面看到的平面图形是( )
A. B. C. D.
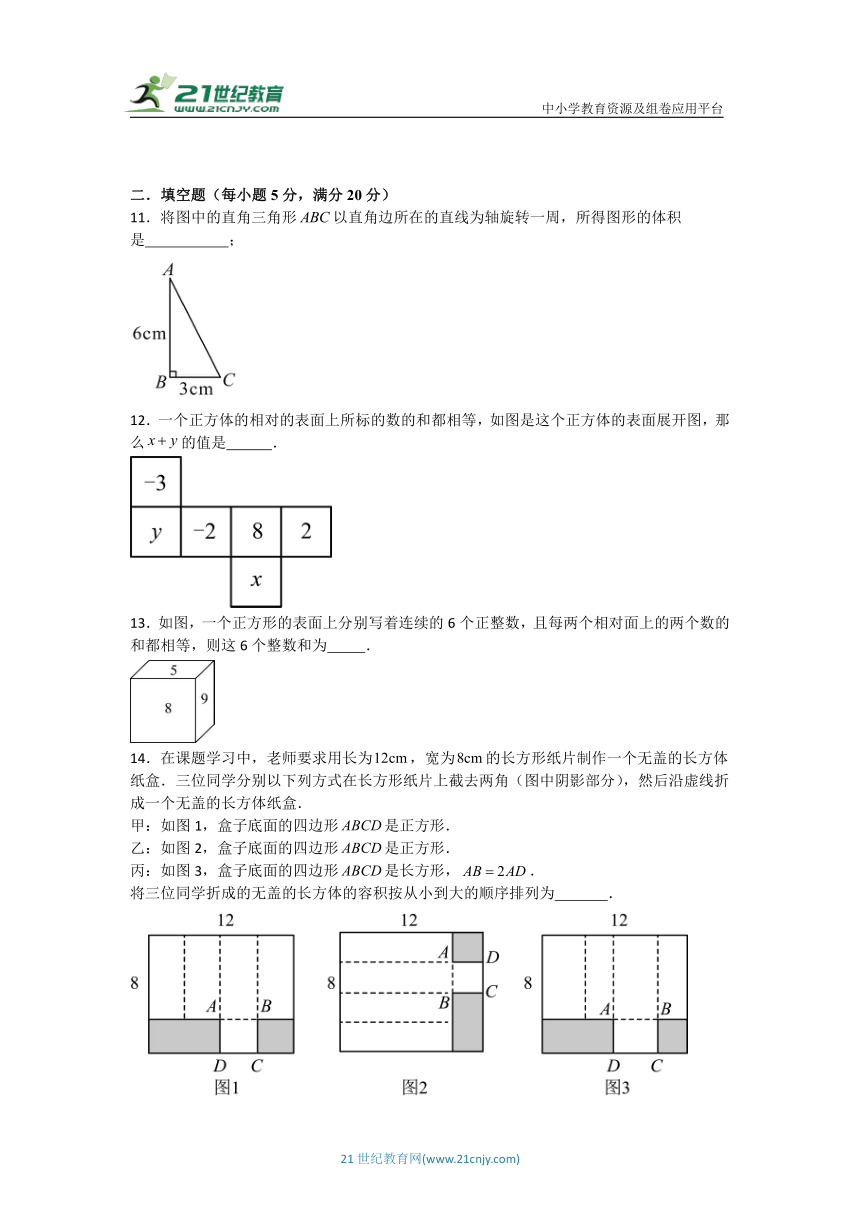
6.(正方体展开图)下列展开图中,( )不能围成正方体.
A.B. C. D.
7.电视剧《西游记》中,孙悟空的“金箍棒”(金箍棒看成一条线)飞速旋转,形成一圆面,这说明了( )
A.点动成线 B.线动成面
C.面动成体 D.两点确定一条直线
8.图1是边长为的正方形纸片,四个角都切去边长为的小正方形后,翻折成一个无盖的长方体纸盒如图2,下列说法错误的是( )
A.
B.该无盖的长方体纸盒的表面积是
C.当时,图2为无盖的正方体纸盒
D.该无盖的长方体纸盒的所有棱长之和是个定值
9.如图所示,某同学用透明的硅胶泥做成一个正方体.并用薄塑料刀竖直切割这个正方体,分成了左右两个长方体和,若这两个长方体的体积之比为,则长方体和的表面展开图的面积之比为( )
A. B. C. D.
10.“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”.用图1所示的“七巧板”中的六块,拼成图2所示的“家”的图形,图1中没用上的那一块七巧板是( )
A.④ B.⑤ C.⑥ D.⑦
二.填空题(每小题5分,满分20分)
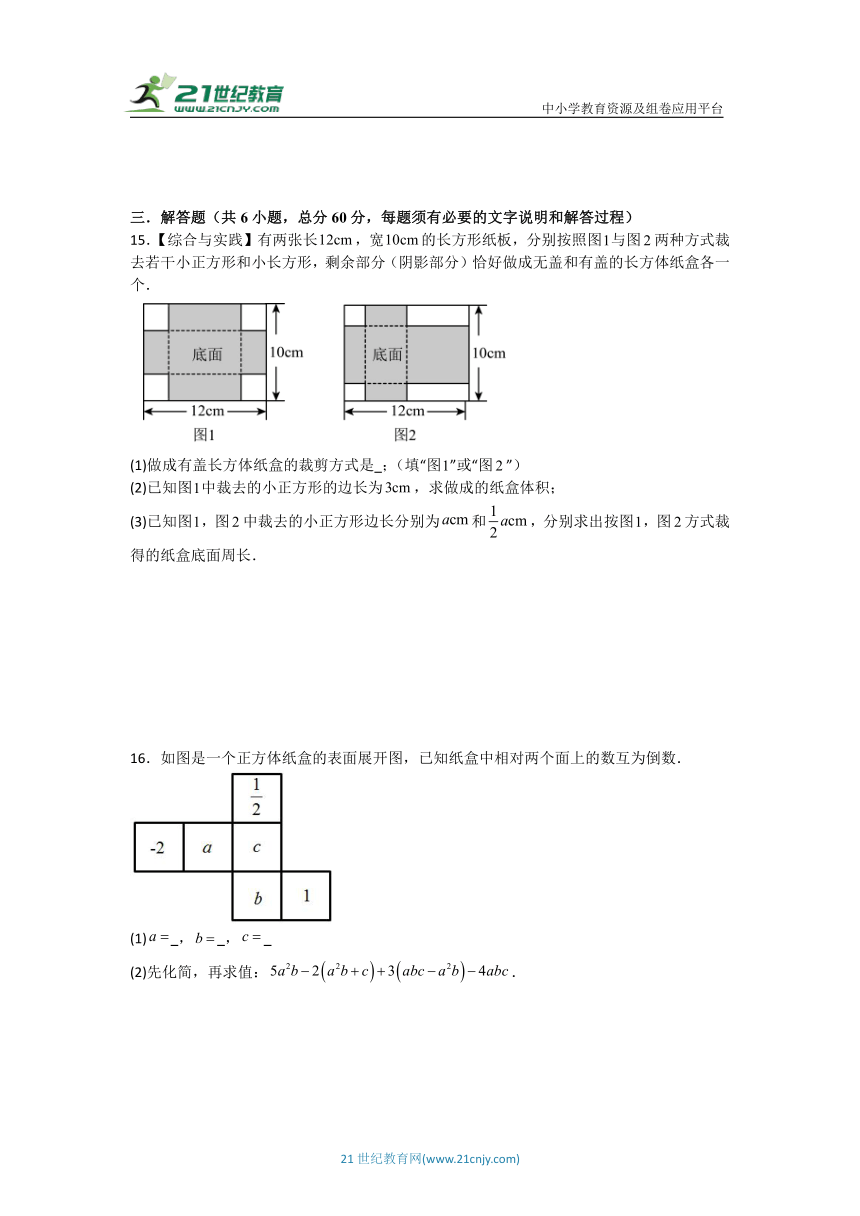
11.将图中的直角三角形以直角边所在的直线为轴旋转一周,所得图形的体积是 ;
12.一个正方体的相对的表面上所标的数的和都相等,如图是这个正方体的表面展开图,那么的值是 .
13.如图,一个正方形的表面上分别写着连续的6个正整数,且每两个相对面上的两个数的和都相等,则这6个整数和为 .
14.在课题学习中,老师要求用长为,宽为的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形是正方形.
乙:如图2,盒子底面的四边形是正方形.
丙:如图3,盒子底面的四边形是长方形,.
将三位同学折成的无盖的长方体的容积按从小到大的顺序排列为 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.【综合与实践】有两张长,宽的长方形纸板,分别按照图与图两种方式裁去若干小正方形和小长方形,剩余部分(阴影部分)恰好做成无盖和有盖的长方体纸盒各一个.
(1)做成有盖长方体纸盒的裁剪方式是 ;(填“图”或“图”)
(2)已知图中裁去的小正方形的边长为,求做成的纸盒体积;
(3)已知图,图中裁去的小正方形边长分别为和,分别求出按图,图方式裁得的纸盒底面周长.
16.如图是一个正方体纸盒的表面展开图,已知纸盒中相对两个面上的数互为倒数.
(1) , ,
(2)先化简,再求值:.
17.如图是某长方体包装盒的展开图,具体数据如图所示,且长方体盒子的长是高的2倍.
(1)展开图的6个面分别标有如图所示的序号,则原包装盒与①相对的面是________(填序号);
(2)若设长方体的高为,则:
①长方体的宽为_______________(用含x的式子表示);
②求长方体包装盒的体积.
18.用个棱长分米的正方体拼成一个几何体,按图的方式摆放在桌面上.
(1)这个几何体覆盖桌面的面积是( )平方分米.
(2)在这个几何体上又添加了两个棱长分米的正方体,得到一个新的几何体.从新几何体的前面看到的图形如图,从上面看到的图形和原来一样.在方格纸上画出从新几何体的上面和左面看到的图形.
19.在平整的地面上,有一个由9个完全相同的小立方块搭成的几何体,每个小正方体的棱长均为,如图所示.
(1)请画出这个几何体从三个方向看到的形状图;
(2)将原几何体露出的表面部分涂成红色,那么红色部分的面积 ___________ .
20.如图是某几何体从三个不同方向看到的形状图.
(1)这个几何体的名称是 ;
(2)若从正面看到的图形的宽为4,长为6,从上面看到的图形是直角三角形,其中斜边长为5,求这个几何体的表面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C B C C B D A B
二、填空题
11.【解】解:①当直角三角形以直角边所在直线为轴旋转一周得到一个圆锥,
所得图形的体积是:;
②当直角三角形以直角边所在直线为轴旋转一周得到一个圆锥,
所得图形的体积是:;
故答案为:或.
12.【解】解:依题意可知,x与是相对面,y与x是相对面,与2是相对面,
相对的表面上所标的数的和都相等,
,,
解得,,
.
故答案为:.
13.【解】解:根据题意分析可得:六个面上分别写着六个连续的整数,
故六个整数可能为5,6,7,8,9,10或4,5,6,7,8,9;
且每个相对面上的两个数之和相等,
,,,
,,(5与8相邻,不合题意,舍去)
∴这六个数是5,6,7,8,9,10,
∴这六个整数的和为:,
故答案为:45.
14.【解】解:由图形并结合题意可得:
甲所折成的无盖长方体的容积为,
乙所折成的无盖长方体的容积为,
丙所折成的无盖长方体的容积为,
所以从小到大排列顺序为乙甲丙,
故答案为:乙甲丙.
三、解答题
15.【解】(1)解:做成有盖长方体纸盒的裁剪方式是:图2;
(2)解:图1中裁去的小正方形边长为,
做成的纸盒的体积;
(3)解:图1的底面周长为,
图2的底面周长为.
16.【解】(1)解:由正方体的平面展开图的特点可知,与1处在相对两个面上,与处在相对两个面上,与处在相对两个面上,
∵正方体纸盒中相对两个面上的数互为倒数,
∴,
故答案为:1,2,.
(2)解:原式
,
将代入得:原式.
17.【解】(1)解:∵长方体展开图的“相间、端”是对面,
∴面和面是相对面,
故答案为:.
(2)解:设长方体的高为,
∴长方体的长为,
∴长方体的宽为:或,
故答案为:或;
∵长方体的宽为:或,
∴,
解得:,
∴长方体的高为:,长方体的长为:,长方体的宽为:,
∴长方体的体积为:,
答:长方体的体积为.
18.【解】(1)
解:从上面看立体图形是,
∵正方体每个面的面积是(平方分米,
∴几何体覆盖桌面的面积是平方分米,
故答案为:;
(2)解:画图如下:
19.【解】(1)解:画出图形如下:
(2);
故答案为:.
20.【解】(1)这个几何体是直三棱柱;
故答案为:直三棱柱;
(2)如图,
∵从正面看到的图形的宽为4,斜边长为5,
∴
由题意可得:它的表面积为:.
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.下面图形经过折叠不能围成棱柱的是( )
A. B. C. D.
2.下列图形中,为三棱柱的侧面展开图的是( )
A. B. C. D.
3.将如图所示的直角三角形绕直线l旋转一周,得到的立体图形是( )
A. B. C. D.
4.如图是一个正方体展开图,图中的六个正方形内分别标有:有、志、者、事、竟、成,将其围成一个正方体后,则与“成”相对的是( )
A.竞 B.有 C.事 D.者
5.一个由5个相同的小正方体组成的立体图形如图所示,则从正面看到的平面图形是( )
A. B. C. D.
6.(正方体展开图)下列展开图中,( )不能围成正方体.
A.B. C. D.
7.电视剧《西游记》中,孙悟空的“金箍棒”(金箍棒看成一条线)飞速旋转,形成一圆面,这说明了( )
A.点动成线 B.线动成面
C.面动成体 D.两点确定一条直线
8.图1是边长为的正方形纸片,四个角都切去边长为的小正方形后,翻折成一个无盖的长方体纸盒如图2,下列说法错误的是( )
A.
B.该无盖的长方体纸盒的表面积是
C.当时,图2为无盖的正方体纸盒
D.该无盖的长方体纸盒的所有棱长之和是个定值
9.如图所示,某同学用透明的硅胶泥做成一个正方体.并用薄塑料刀竖直切割这个正方体,分成了左右两个长方体和,若这两个长方体的体积之比为,则长方体和的表面展开图的面积之比为( )
A. B. C. D.
10.“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”.用图1所示的“七巧板”中的六块,拼成图2所示的“家”的图形,图1中没用上的那一块七巧板是( )
A.④ B.⑤ C.⑥ D.⑦
二.填空题(每小题5分,满分20分)
11.将图中的直角三角形以直角边所在的直线为轴旋转一周,所得图形的体积是 ;
12.一个正方体的相对的表面上所标的数的和都相等,如图是这个正方体的表面展开图,那么的值是 .
13.如图,一个正方形的表面上分别写着连续的6个正整数,且每两个相对面上的两个数的和都相等,则这6个整数和为 .
14.在课题学习中,老师要求用长为,宽为的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形是正方形.
乙:如图2,盒子底面的四边形是正方形.
丙:如图3,盒子底面的四边形是长方形,.
将三位同学折成的无盖的长方体的容积按从小到大的顺序排列为 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.【综合与实践】有两张长,宽的长方形纸板,分别按照图与图两种方式裁去若干小正方形和小长方形,剩余部分(阴影部分)恰好做成无盖和有盖的长方体纸盒各一个.
(1)做成有盖长方体纸盒的裁剪方式是 ;(填“图”或“图”)
(2)已知图中裁去的小正方形的边长为,求做成的纸盒体积;
(3)已知图,图中裁去的小正方形边长分别为和,分别求出按图,图方式裁得的纸盒底面周长.
16.如图是一个正方体纸盒的表面展开图,已知纸盒中相对两个面上的数互为倒数.
(1) , ,
(2)先化简,再求值:.
17.如图是某长方体包装盒的展开图,具体数据如图所示,且长方体盒子的长是高的2倍.
(1)展开图的6个面分别标有如图所示的序号,则原包装盒与①相对的面是________(填序号);
(2)若设长方体的高为,则:
①长方体的宽为_______________(用含x的式子表示);
②求长方体包装盒的体积.
18.用个棱长分米的正方体拼成一个几何体,按图的方式摆放在桌面上.
(1)这个几何体覆盖桌面的面积是( )平方分米.
(2)在这个几何体上又添加了两个棱长分米的正方体,得到一个新的几何体.从新几何体的前面看到的图形如图,从上面看到的图形和原来一样.在方格纸上画出从新几何体的上面和左面看到的图形.
19.在平整的地面上,有一个由9个完全相同的小立方块搭成的几何体,每个小正方体的棱长均为,如图所示.
(1)请画出这个几何体从三个方向看到的形状图;
(2)将原几何体露出的表面部分涂成红色,那么红色部分的面积 ___________ .
20.如图是某几何体从三个不同方向看到的形状图.
(1)这个几何体的名称是 ;
(2)若从正面看到的图形的宽为4,长为6,从上面看到的图形是直角三角形,其中斜边长为5,求这个几何体的表面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C B C C B D A B
二、填空题
11.【解】解:①当直角三角形以直角边所在直线为轴旋转一周得到一个圆锥,
所得图形的体积是:;
②当直角三角形以直角边所在直线为轴旋转一周得到一个圆锥,
所得图形的体积是:;
故答案为:或.
12.【解】解:依题意可知,x与是相对面,y与x是相对面,与2是相对面,
相对的表面上所标的数的和都相等,
,,
解得,,
.
故答案为:.
13.【解】解:根据题意分析可得:六个面上分别写着六个连续的整数,
故六个整数可能为5,6,7,8,9,10或4,5,6,7,8,9;
且每个相对面上的两个数之和相等,
,,,
,,(5与8相邻,不合题意,舍去)
∴这六个数是5,6,7,8,9,10,
∴这六个整数的和为:,
故答案为:45.
14.【解】解:由图形并结合题意可得:
甲所折成的无盖长方体的容积为,
乙所折成的无盖长方体的容积为,
丙所折成的无盖长方体的容积为,
所以从小到大排列顺序为乙甲丙,
故答案为:乙甲丙.
三、解答题
15.【解】(1)解:做成有盖长方体纸盒的裁剪方式是:图2;
(2)解:图1中裁去的小正方形边长为,
做成的纸盒的体积;
(3)解:图1的底面周长为,
图2的底面周长为.
16.【解】(1)解:由正方体的平面展开图的特点可知,与1处在相对两个面上,与处在相对两个面上,与处在相对两个面上,
∵正方体纸盒中相对两个面上的数互为倒数,
∴,
故答案为:1,2,.
(2)解:原式
,
将代入得:原式.
17.【解】(1)解:∵长方体展开图的“相间、端”是对面,
∴面和面是相对面,
故答案为:.
(2)解:设长方体的高为,
∴长方体的长为,
∴长方体的宽为:或,
故答案为:或;
∵长方体的宽为:或,
∴,
解得:,
∴长方体的高为:,长方体的长为:,长方体的宽为:,
∴长方体的体积为:,
答:长方体的体积为.
18.【解】(1)
解:从上面看立体图形是,
∵正方体每个面的面积是(平方分米,
∴几何体覆盖桌面的面积是平方分米,
故答案为:;
(2)解:画图如下:
19.【解】(1)解:画出图形如下:
(2);
故答案为:.
20.【解】(1)这个几何体是直三棱柱;
故答案为:直三棱柱;
(2)如图,
∵从正面看到的图形的宽为4,斜边长为5,
∴
由题意可得:它的表面积为:.
同课章节目录
