第二章代数式单元测试卷(含答案)湘教版2025—2026学年七年级上册
文档属性
| 名称 | 第二章代数式单元测试卷(含答案)湘教版2025—2026学年七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 547.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 20:29:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二章代数式单元测试卷湘教版2025—2026学年七年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.下列计算正确的是( )
A. B.
C. D.
2.多项式按字母的降幂排列正确的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.单项式的系数是
B.与不是同类项
C.最大的负整数是
D.多项式的次数是
4.已知代数式的值是3,则代数式的值为( )
A.8 B.9 C.10 D.11
5.一艘江轮在静水中的速度为,逆流速度为,则顺流速度为(顺流航行的速度=静水中速度+水流速度;逆流航行的速度=静水中速度水流速度)( )
A. B.
C. D.
6.若,,且,则的值为( )
A.2 B. C.2或8 D.8或
7.若代数式的值与的取值无关,则的值为( )
A. B. C. D.
8.有理数在数轴上的位置如图所示,则化简的结果是( )
A. B. C. D.
9.已知整数,,,满足下列条件:,,,,,以此类推,则的值为( )
A.1010 B.1011 C.1012 D.1013
10.如图所示的是一个大长方形,它被分割成4个大小不同的正方形①②③④和一个小长方形⑤,有下列结论:
(1)若已知正方形①和②的周长,就能求出大长方形的周长;
(2)若已知正方形③的周长,就能求出大长方形的周长;
(3)若已知正方形④的周长,就能求出大长方形的周长;
(4)若已知小长方形⑤的周长,就能求出大长方形的周长.其中正确的个数为( )
A. B. C. D.
二.填空题(每小题5分,满分20分)
11.若,则 .
12.由火柴棒摆成的3个图案如图所示,按图中规律摆放,则第n个图案需要 根火柴棒.
13.已知,,,则代数式的值为
14.已知关于的多项式化简后不含项,则的值是
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.先化简,再求值.
(1),其中,;
(2),其中.
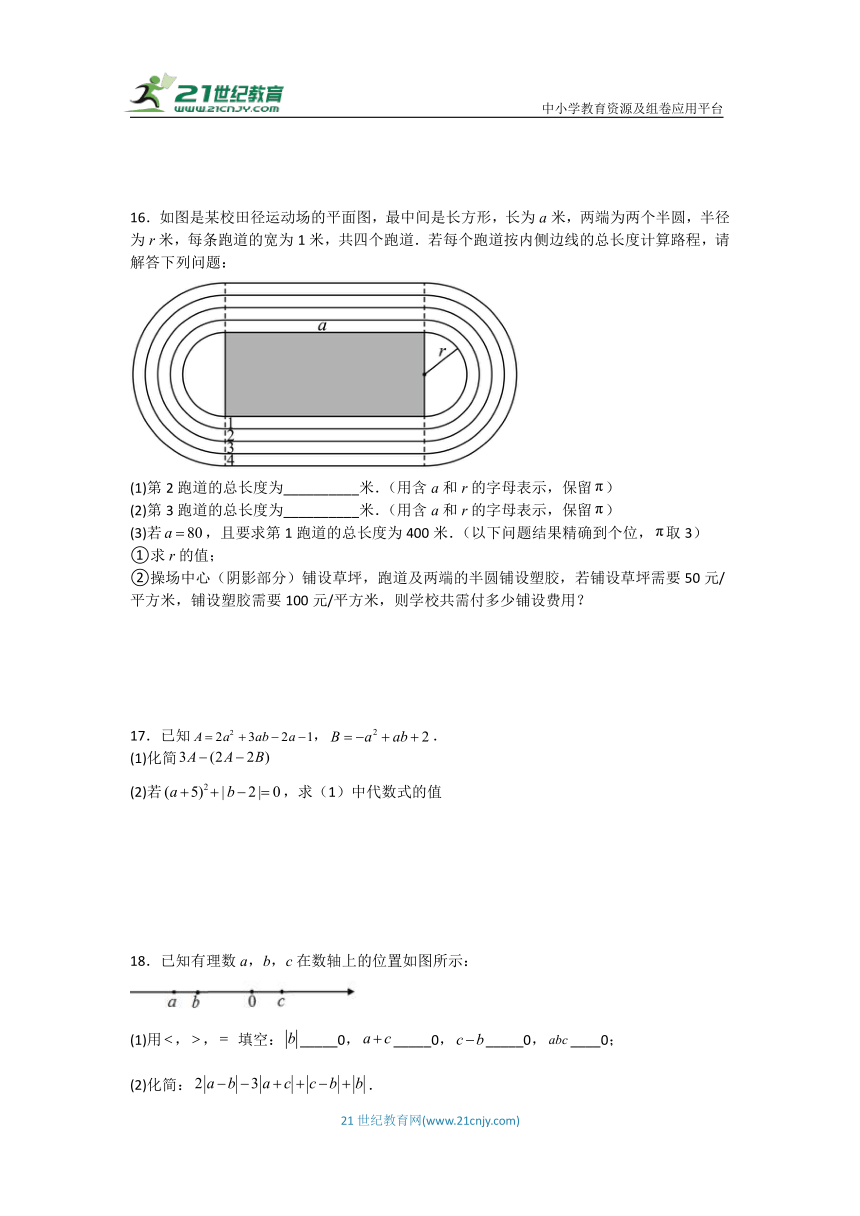
16.如图是某校田径运动场的平面图,最中间是长方形,长为a米,两端为两个半圆,半径为r米,每条跑道的宽为1米,共四个跑道.若每个跑道按内侧边线的总长度计算路程,请解答下列问题:
(1)第2跑道的总长度为__________米.(用含a和r的字母表示,保留)
(2)第3跑道的总长度为__________米.(用含a和r的字母表示,保留)
(3)若,且要求第1跑道的总长度为400米.(以下问题结果精确到个位,取3)
①求r的值;
②操场中心(阴影部分)铺设草坪,跑道及两端的半圆铺设塑胶,若铺设草坪需要50元/平方米,铺设塑胶需要100元/平方米,则学校共需付多少铺设费用?
17.已知,.
(1)化简
(2)若,求(1)中代数式的值
18.已知有理数a,b,c在数轴上的位置如图所示:
(1)用,, 填空:_____0,_____0,_____0,____0;
(2)化简:.
19.【观察思考】
【规律发现】
(1)观察各图案中灰色菱形和白色菱形的个数,绘制表格如下.
第1个图案 第2个图案 第3个图案 第4个图案 第5个图案 第6个图案 …
灰色菱形个数 1 2 5 8 13 b …
白色菱形个数 0 2 4 8 a 18 …
小菱形总个数 1 4 9 16 25 c …
填空:表格中,________,________,________.
(2)请写出第n个图案中灰色菱形,白色菱形各有几个.
【规律应用】
(3)某小区计划用边长为1米的菱形砖铺设一块菱形区域,该菱形区域边长为45米,若按以上规律图案进行设计,则需要购买的灰色菱形砖,白色菱形砖各多少块?
20.已知多项式.
(1)若多项式的值与字母的取值无关,求的值;
(2)在(1)的条件下,求多项式的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C A A D C D C C
二、填空题
11.【解】解:∵,
∴,
∴,
∴,
故答案为:6.
12.【解】解:根据题意,
第一图案有根火柴;
第2个图案中有根火柴;
第3个图案中有根火柴;
第n个图案中有根火柴,
故答案为:.
13.【解】解:,,
,,,
当,,时,原式
当、、中有一正两负时,不妨设,,,
原式
当、、中有两正一负时,不妨设,,,
原式
当,,时,
原式
综上,原式的值是或,
故答案为:或.
14.【解】解:
,
由题意得:,
解得:
故答案为:2.
三、解答题
15.【解】(1)解:原式
,
当时,原式
(2)解:原式
,
当时,原式.
16.【解】(1)解:第2跑道的直道总长为米,弯道总长为米,跑道总长度为米;
故答案为:;
(2)解:第3跑道的总长度为米;
故答案为:;
(3)解:①由题意可得:,
∵,
∴;
②由题意可得:
铺设草坪费用为:(元),
铺设塑胶费用为:(元),
∴(元),
∴学校共需付这两项铺设费用为964800元.
17.【解】(1)解:∵,
∴
(2)解:∵,
∴,
∴,,
∴原式.
18.【解】(1)解:由数轴可知,,且,
,,,,
故答案为:,,,;
(2)解:由数轴可知,,且,
∴,,,
∴
19.【解】解:(1)由所给图形可知,
第1个图案中灰色菱形的个数为:,白色菱形的个数为:,小菱形的总个数为:;
第2个图案中灰色菱形的个数为:,白色菱形的个数为:,小菱形的总个数为:;
第3个图案中灰色菱形的个数为:,白色菱形的个数为:,小菱形的总个数为:;
第4个图案中灰色菱形的个数为:,白色菱形的个数为:,小菱形的总个数为:;
…,
所以当n为奇数时,第n个图案中灰色菱形的个数为个,白色菱形的个数为个;
当n为偶数时,第n个图案中灰色菱形和白色菱形的个数都是个,
第n个图形中小菱形的总个数为个.
当时,;
当时,,.
故答案为:12,18,36.
(2)由(1)知,
当n为奇数时,第n个图案中灰色菱形的个数为个,白色菱形的个数为个;当n为偶数时,第n个图案中灰色菱形和白色菱形的个数都是个.
(3)由(1)知,当时,,,
所以需要购买1013块灰色菱形砖,1012块白色菱形砖.
20.【解】(1)解:∵
,
∵多项式的值与字母的取值无关,
,,
解得:,;
(2)
当,时,原式.
21世纪教育网(www.21cnjy.com)
第二章代数式单元测试卷湘教版2025—2026学年七年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.下列计算正确的是( )
A. B.
C. D.
2.多项式按字母的降幂排列正确的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.单项式的系数是
B.与不是同类项
C.最大的负整数是
D.多项式的次数是
4.已知代数式的值是3,则代数式的值为( )
A.8 B.9 C.10 D.11
5.一艘江轮在静水中的速度为,逆流速度为,则顺流速度为(顺流航行的速度=静水中速度+水流速度;逆流航行的速度=静水中速度水流速度)( )
A. B.
C. D.
6.若,,且,则的值为( )
A.2 B. C.2或8 D.8或
7.若代数式的值与的取值无关,则的值为( )
A. B. C. D.
8.有理数在数轴上的位置如图所示,则化简的结果是( )
A. B. C. D.
9.已知整数,,,满足下列条件:,,,,,以此类推,则的值为( )
A.1010 B.1011 C.1012 D.1013
10.如图所示的是一个大长方形,它被分割成4个大小不同的正方形①②③④和一个小长方形⑤,有下列结论:
(1)若已知正方形①和②的周长,就能求出大长方形的周长;
(2)若已知正方形③的周长,就能求出大长方形的周长;
(3)若已知正方形④的周长,就能求出大长方形的周长;
(4)若已知小长方形⑤的周长,就能求出大长方形的周长.其中正确的个数为( )
A. B. C. D.
二.填空题(每小题5分,满分20分)
11.若,则 .
12.由火柴棒摆成的3个图案如图所示,按图中规律摆放,则第n个图案需要 根火柴棒.
13.已知,,,则代数式的值为
14.已知关于的多项式化简后不含项,则的值是
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.先化简,再求值.
(1),其中,;
(2),其中.
16.如图是某校田径运动场的平面图,最中间是长方形,长为a米,两端为两个半圆,半径为r米,每条跑道的宽为1米,共四个跑道.若每个跑道按内侧边线的总长度计算路程,请解答下列问题:
(1)第2跑道的总长度为__________米.(用含a和r的字母表示,保留)
(2)第3跑道的总长度为__________米.(用含a和r的字母表示,保留)
(3)若,且要求第1跑道的总长度为400米.(以下问题结果精确到个位,取3)
①求r的值;
②操场中心(阴影部分)铺设草坪,跑道及两端的半圆铺设塑胶,若铺设草坪需要50元/平方米,铺设塑胶需要100元/平方米,则学校共需付多少铺设费用?
17.已知,.
(1)化简
(2)若,求(1)中代数式的值
18.已知有理数a,b,c在数轴上的位置如图所示:
(1)用,, 填空:_____0,_____0,_____0,____0;
(2)化简:.
19.【观察思考】
【规律发现】
(1)观察各图案中灰色菱形和白色菱形的个数,绘制表格如下.
第1个图案 第2个图案 第3个图案 第4个图案 第5个图案 第6个图案 …
灰色菱形个数 1 2 5 8 13 b …
白色菱形个数 0 2 4 8 a 18 …
小菱形总个数 1 4 9 16 25 c …
填空:表格中,________,________,________.
(2)请写出第n个图案中灰色菱形,白色菱形各有几个.
【规律应用】
(3)某小区计划用边长为1米的菱形砖铺设一块菱形区域,该菱形区域边长为45米,若按以上规律图案进行设计,则需要购买的灰色菱形砖,白色菱形砖各多少块?
20.已知多项式.
(1)若多项式的值与字母的取值无关,求的值;
(2)在(1)的条件下,求多项式的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C A A D C D C C
二、填空题
11.【解】解:∵,
∴,
∴,
∴,
故答案为:6.
12.【解】解:根据题意,
第一图案有根火柴;
第2个图案中有根火柴;
第3个图案中有根火柴;
第n个图案中有根火柴,
故答案为:.
13.【解】解:,,
,,,
当,,时,原式
当、、中有一正两负时,不妨设,,,
原式
当、、中有两正一负时,不妨设,,,
原式
当,,时,
原式
综上,原式的值是或,
故答案为:或.
14.【解】解:
,
由题意得:,
解得:
故答案为:2.
三、解答题
15.【解】(1)解:原式
,
当时,原式
(2)解:原式
,
当时,原式.
16.【解】(1)解:第2跑道的直道总长为米,弯道总长为米,跑道总长度为米;
故答案为:;
(2)解:第3跑道的总长度为米;
故答案为:;
(3)解:①由题意可得:,
∵,
∴;
②由题意可得:
铺设草坪费用为:(元),
铺设塑胶费用为:(元),
∴(元),
∴学校共需付这两项铺设费用为964800元.
17.【解】(1)解:∵,
∴
(2)解:∵,
∴,
∴,,
∴原式.
18.【解】(1)解:由数轴可知,,且,
,,,,
故答案为:,,,;
(2)解:由数轴可知,,且,
∴,,,
∴
19.【解】解:(1)由所给图形可知,
第1个图案中灰色菱形的个数为:,白色菱形的个数为:,小菱形的总个数为:;
第2个图案中灰色菱形的个数为:,白色菱形的个数为:,小菱形的总个数为:;
第3个图案中灰色菱形的个数为:,白色菱形的个数为:,小菱形的总个数为:;
第4个图案中灰色菱形的个数为:,白色菱形的个数为:,小菱形的总个数为:;
…,
所以当n为奇数时,第n个图案中灰色菱形的个数为个,白色菱形的个数为个;
当n为偶数时,第n个图案中灰色菱形和白色菱形的个数都是个,
第n个图形中小菱形的总个数为个.
当时,;
当时,,.
故答案为:12,18,36.
(2)由(1)知,
当n为奇数时,第n个图案中灰色菱形的个数为个,白色菱形的个数为个;当n为偶数时,第n个图案中灰色菱形和白色菱形的个数都是个.
(3)由(1)知,当时,,,
所以需要购买1013块灰色菱形砖,1012块白色菱形砖.
20.【解】(1)解:∵
,
∵多项式的值与字母的取值无关,
,,
解得:,;
(2)
当,时,原式.
21世纪教育网(www.21cnjy.com)
同课章节目录
