2.1.3代数式:探索规律 课件(共45张PPT) 沪科版(2024)数学七年级上册
文档属性
| 名称 | 2.1.3代数式:探索规律 课件(共45张PPT) 沪科版(2024)数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 955.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
代数式
-----探索规律
课前检测(5分钟)
1.按正确书写要求书写代数式
2.一个两位数的个位数字是a,十位数字是b,请用代数式表示这个两位数.
3.用代数式表示:数a的倒数与b的差的3倍为 .
4.代数式 (a–b) 的意义是________________.
5.用代数式表示: a与b的平方的和 .
例 结合你的生活经验对下列代数式作出具体解释:
(1)a – b (2) ab
解:(1) 今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a – b)岁;
(2) 长方形的长为a厘米,宽为b厘米,长方形的面积是ab平方厘米
例下列代数式,哪些书写不够规范,请改正过来
(1)5×a (2)m×n (3)4×(a+b) (4)3x+1 (5)m×n-3 (6)3×y
小结:1、能够用简单的语言表达代数式。2、写代数式时要注意三点:
(1)、代数式中出现乘号通常写成“ . ”或省略不写;
(2)、数字与字母相乘,数字写在前,字母写在后;
(3) 、除法运算写成分数形式
小试牛刀
仔细观察,按规律填空:
(1)、1,2,3,4, ,
(2)、2,4,6,8, ,
(3)、1,4,7,10, ,
5
10
13
2、找规律
① 2,4,8,16,___……(第n个数)_____
变式3,5,9,17, ___……(第n个数)_____
② 6,12,18,24, ___……(第n个数)_____
变式8,14,20,26,____……(第n个数)_______
32
2n
33
2n+1
30
6n
32
6n+2
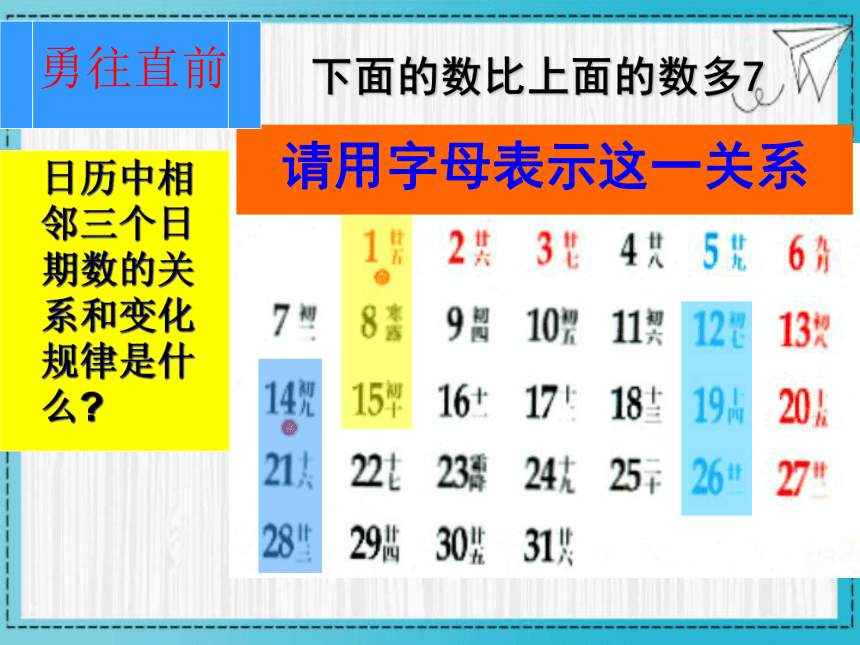
日历中相邻三个日期数的关系和变化规律是什么
后面的数比前面的数多1
请用字母表示这一关系
活动 一
下面的数比上面的数多7
请用字母表示这一关系
日历中相邻三个日期数的关系和变化规律是什么
勇往直前
(1) 日历中3×3方框内九数之和与方框中正中间的数有何等量关系?
矩形方框中九数之和等于中间数的9倍
探究活动
探究活动
这个关系在其它方框中成立吗
成立!
a
a-7
a+8
a-6
a-8
a+6
a+7
a-1
a+1
(a-8)+(a-7)+(a-6)+(a-1)+a+
(a+1)+(a+6)+(a+7)+(a+8) = ______
9a
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
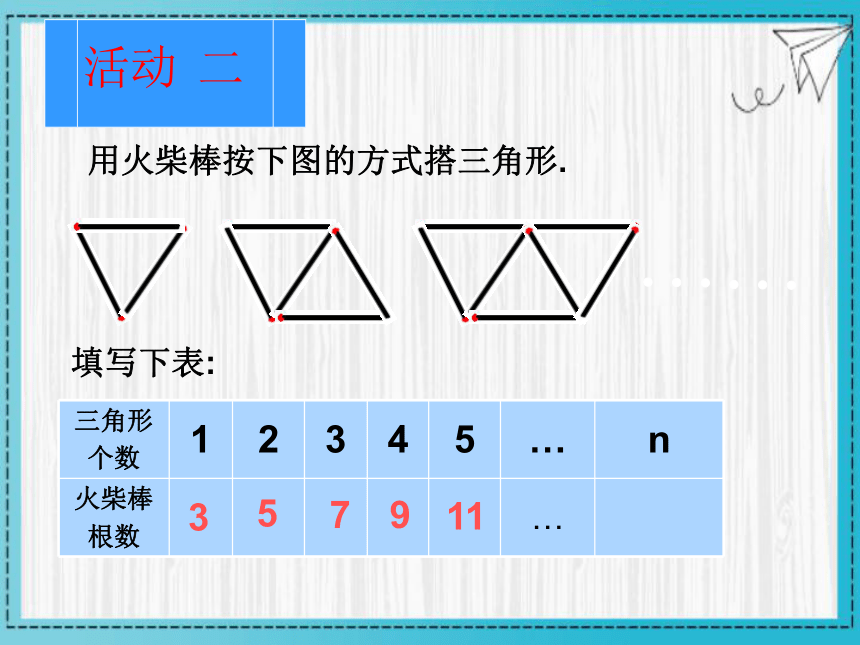
用火柴棒按下图的方式搭三角形.
三角形 个数 1 2 3 4 5 … n
火柴棒 根数 …
填写下表:
3
5
7
9
11
活动 二
三角形个数 火柴棒根数
1
2
3
4
5
…
n
3
+2
+2
+2
+2
+2
1+2
三角形个数 1 2 3 4 5 … n
火柴棒根数 …
3
5
7
9
11
2n+1
3=1+2
5=1+2+2
7=1+2+2+2
9=1+2+2+2+2
11=1+2+2+2+2+2
……
=1+2+2+2+2+2+2+…+2
1+2n
做题方法
探索规律的一般步骤:
猜 想 规 律
表 示 规 律
验 证 规 律
观 察 特 例
1、按左图方式摆放餐桌和椅子
(1) 1张餐桌可坐___人;
2张餐桌可坐___人.
(2) 按照左图的方式继续排列餐桌,完成下表:
桌子 张数 1 2 3 4 5 … n
可坐 人数 …
6
10
14
18
22
6
10
试一试
4
4
+4
+4
+4
……
(4n+2)
n张餐桌可坐 人
练一练(2):
如图是6月的日历。现用一个矩形在日历中任意框出4个数,
请你用一个等式表示a、b、c、d之间的关系:
。
a b
c d
a+d=b+c
a-c=b-d
3、研究下列算式,你发现了什么规律?
用字母表示这个规律.
1×3+1=22;
2×4+1=32;
3×5+1=42;
4×6+1=52;
……………
用n表示自然数,规律
是: 。
n(n+2)+1=(n+1)2
这节课你有什么收获?
请和你的同桌进行交流。
探索规律时遇到挫折,你会怎么办?
慧眼看出来
3n+1
2007a2007
1、4,7,10,13,16,19,…….,第n项为 _______.
2、a,-2a2,3a3,-4a4,5a5,-6a6,……. ,第2007项为________.
3、 , , , ……,第n项为_______.
1
3
1
5
1
7
1
9
1
2n+1
用火柴棒按以下方式搭小鱼
搭n条这样的小鱼需要多少根火柴棒?与同学交流。
搭20条这样的小鱼需要多少根火柴棒?
搭100条呢?
搭1条小鱼用___根火柴棒,搭2条小鱼用__根,搭3条小鱼用___根……每多搭1条小鱼增加___根火柴棒,搭n条小鱼需要____________根火柴棒。
8
14
20
6
[8+6(n-1)]
4
7
10
13
3n+1
……
火柴根数
4
3
2
1
正方形个数
例4、搭一搭,填一填:
(1)我们按如图的摆法搭一行正方形。记录你所搭的正方形的个数和所用的火柴棒的根数,并填表:
n
……
引题:
如图:工地上有一堆圆形钢管,第一层有2根,第二层3根,第三层4根,……
你能说出从第一层到第八层共有多少根吗?到第n层共有多少根呢?
……
解:当 n=8时,共有8×(8+3) ÷2=44根
n(n+3)
2
按下图方式摆放餐桌和椅子:
(1)1张餐桌可坐6人,2张餐桌可 人。
(2)按照上图的方式继续排列餐桌,完成下表:
桌子张数 3 4 5 6 ……
可坐人数
4+4
+4+2
4+4
+4+4+2
4+4+4+4+4+2
4+4+4
+4+4+4+2
4+4+2
……
(3)探索餐桌张数n与可坐人数w之间的关系。
W=4n+2
(4) 15张餐桌这样排,可坐多少人?
解:当n= 15时,w=4×15+2=62
别忘了
验证!
10
14
18
22
26
若按下图方式将桌子拼在一起。
(1)2张桌子拼在一起可坐 人,3张桌子可坐 人,n张桌子可坐 人。
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐 人;
(3)在(2)中,若改成每8张桌子拼成1张大桌子,则共可坐 人。
2×2+4
2n+4
112
100
2×3+4
练习:某种药品的数量与总价关系如下表:
写出药品数量x(克)与总价y(元)之间的关系。
y=2x+0.1
数量(克) 总价(元)
1 2.1
2 4.1
3 6.1
4 8.1
…… ……
=2+0.1
=4+0.1
=6+0.1
=8+0.1
1、你能搭出其他图形吗?并解决类似的问题?
课堂检测
n个三角形呢?
n层 呢?
2、下面的图形是由边长为1的正方形按照某种规律排列而组成的.
(1)观察图形,填写下表:
图形 ① ② ③
正方形的个数 8
(2)推测第n个图形中,正方形的个数为________ (用含n的代数式表示).
13
18
3、观察下面一列数:1,2,3,4,5,6,7,...,将这列数排成下列形式:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
… … … … … … … … … … …
按照上述规律排下去,那么第10行从左边第9个数是_______.
游戏规则 第一位同学将拿到的数字乘以2传给第二位同学,第二位同学将拿到的数加上3传给第三位同学,第三位同学将得到的数平方后传给第四位同学,第四位同学把结果减去5后传给第五位同学,第五位同学迅速将结果写在黑板上。
x
2x
2x+3
(2x+3)
(2x+3) -5
游戏
用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值。
例1.当a=3,b= -1时,求下列各代数式的值。
(1)(a+b) , (2) a +2ab+b , (3) (a-b) ,
(4) a -2ab+b
解:(1)当a=3,b= -1时,
(a+b) =[3+ (-1 )] =
(2)当a=3,b= -1时,
a +2ab+b =3 +2×3× (-1)+(-1)
=9+(-6)+1=
2 =4
4
(1)格式: “ 当 …… 时 ”
(2)代入时,数字要代入对应的字母的位置去;
(3)在求值时,原来省略的乘号要添上
( 4 )若代入 的是负数或分数,必须加上括号。
在我们求“代数式的值”时,有哪些是需要我们注意的呢?
解:(1)当a=3,b= -1时,
(a+b) =[3+(-1)] = 2 =4
(2)当a=3,b= -1时,
a +2ab+b =3 +2×3× (-1)+(-1)
=9+(-6)+1= 4
按右边图示的程序计算,若开始输入的n值为3,则最后输出的结果是 。
231
输入n
计算 的值
>200
输出结果
yes
no
你读懂了吗
挑战自我
1.若a+b=-1,求代数式
(1)a+b+2;
(2)3a+3b的值.
相同的代数式可以看作一个整体——整体代换.
解:∵a+b=-1
∴a+b+2=(-1)+2=1
解:∵a+b=-1
∴3a+3b+2=3(a+b)+2=3x(-1)+2
=-1
整体带入法
例1、若 的值为7,求代数式 的值。
解:由已知 ,则
=3 +4
(逆用乘法分配律)
例2、若2b-a=5,求代数式5(a-2b)2-3(a-2b)-60的值。
解:∵2b-a=5,∴a-2b=-5
∴ 5(a-2b)2-3(a-2b)-60=5×(-5)2-3×(-5)-60
=125+15-60
=80
1.代数式
挑战你自己
|x| - 5
________
x
中,x不能取的值是____;
x
_________
|x| - 5
中,x不能取得值是_____________.
0
+5与-5
2.已知x+y=5,求2(x+y) - ——— - (x+y)+1的值为 _________
10
x+y
44
4(a-b)
a+b
a+b
a-b
3.已知 ——
a-b
a+b
=3,则代数式 —— - —— 的
值为________
5
3
——
练习:
(1)若 ,则 ;
(2) 若 ,则 ;
(3) 若 ,则 ;
24
15
8
(4) 若 ,则 。
小结
1、求代数式的值的步骤:(1)写出字母的值,(2)代入,(3)计算;
2、求代数式的值的注意事项:
(1)代入数值前应先指明字母的取值,把“当……时”写出来。
(2)如果字母的值是负数、分数,并且要计算它的乘方,代入时应加上括号;
(3)代数式中省略了乘号时,代入数值以后必须添上乘号。
3、相同的代数式可以看作一个字母——整体代换。
4、代数式的值的广泛应用:计算机编程(包括用Excel处理数据等)、经济、生活等方面的应用。
试一试
1.若梯形的上底为a,下底为b,高为h,则
梯形的面积为_______________,
当a=2cm,b=3cm,h=4cm时,
s梯=____________.
S梯=
(a+b)h
10cm
2.测得某弹簧的长度y(厘米)与挂重x(千克)有下表关系(该弹簧挂重不得超过20千克):
X(千克) 0 1 2 3 ……
Y(厘米) 4 4.2 4.4 4.6 ……
(1)写出y与x的关系式:
(2)计算当弹簧的长度为5.6厘米的弹簧挂重.
3. 已知 ,求代数式
的值.
试一试
课后思考
若a2=1,则3a2=______
变式一:若a2+a=1,则3(a2+a)=______
变式二:若a2+a=1,则3a2+3a-5=______
变式三:若a2+a+3=0,则3a2+3a-5=______
1、今天星期五,再过100天星期几?
2、比较大小:
挑战自我,极限冲刺:
愿同学们越来越
聪明
不畏艰险,迎难而上!
代数式
-----探索规律
课前检测(5分钟)
1.按正确书写要求书写代数式
2.一个两位数的个位数字是a,十位数字是b,请用代数式表示这个两位数.
3.用代数式表示:数a的倒数与b的差的3倍为 .
4.代数式 (a–b) 的意义是________________.
5.用代数式表示: a与b的平方的和 .
例 结合你的生活经验对下列代数式作出具体解释:
(1)a – b (2) ab
解:(1) 今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a – b)岁;
(2) 长方形的长为a厘米,宽为b厘米,长方形的面积是ab平方厘米
例下列代数式,哪些书写不够规范,请改正过来
(1)5×a (2)m×n (3)4×(a+b) (4)3x+1 (5)m×n-3 (6)3×y
小结:1、能够用简单的语言表达代数式。2、写代数式时要注意三点:
(1)、代数式中出现乘号通常写成“ . ”或省略不写;
(2)、数字与字母相乘,数字写在前,字母写在后;
(3) 、除法运算写成分数形式
小试牛刀
仔细观察,按规律填空:
(1)、1,2,3,4, ,
(2)、2,4,6,8, ,
(3)、1,4,7,10, ,
5
10
13
2、找规律
① 2,4,8,16,___……(第n个数)_____
变式3,5,9,17, ___……(第n个数)_____
② 6,12,18,24, ___……(第n个数)_____
变式8,14,20,26,____……(第n个数)_______
32
2n
33
2n+1
30
6n
32
6n+2
日历中相邻三个日期数的关系和变化规律是什么
后面的数比前面的数多1
请用字母表示这一关系
活动 一
下面的数比上面的数多7
请用字母表示这一关系
日历中相邻三个日期数的关系和变化规律是什么
勇往直前
(1) 日历中3×3方框内九数之和与方框中正中间的数有何等量关系?
矩形方框中九数之和等于中间数的9倍
探究活动
探究活动
这个关系在其它方框中成立吗
成立!
a
a-7
a+8
a-6
a-8
a+6
a+7
a-1
a+1
(a-8)+(a-7)+(a-6)+(a-1)+a+
(a+1)+(a+6)+(a+7)+(a+8) = ______
9a
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
用火柴棒按下图的方式搭三角形.
三角形 个数 1 2 3 4 5 … n
火柴棒 根数 …
填写下表:
3
5
7
9
11
活动 二
三角形个数 火柴棒根数
1
2
3
4
5
…
n
3
+2
+2
+2
+2
+2
1+2
三角形个数 1 2 3 4 5 … n
火柴棒根数 …
3
5
7
9
11
2n+1
3=1+2
5=1+2+2
7=1+2+2+2
9=1+2+2+2+2
11=1+2+2+2+2+2
……
=1+2+2+2+2+2+2+…+2
1+2n
做题方法
探索规律的一般步骤:
猜 想 规 律
表 示 规 律
验 证 规 律
观 察 特 例
1、按左图方式摆放餐桌和椅子
(1) 1张餐桌可坐___人;
2张餐桌可坐___人.
(2) 按照左图的方式继续排列餐桌,完成下表:
桌子 张数 1 2 3 4 5 … n
可坐 人数 …
6
10
14
18
22
6
10
试一试
4
4
+4
+4
+4
……
(4n+2)
n张餐桌可坐 人
练一练(2):
如图是6月的日历。现用一个矩形在日历中任意框出4个数,
请你用一个等式表示a、b、c、d之间的关系:
。
a b
c d
a+d=b+c
a-c=b-d
3、研究下列算式,你发现了什么规律?
用字母表示这个规律.
1×3+1=22;
2×4+1=32;
3×5+1=42;
4×6+1=52;
……………
用n表示自然数,规律
是: 。
n(n+2)+1=(n+1)2
这节课你有什么收获?
请和你的同桌进行交流。
探索规律时遇到挫折,你会怎么办?
慧眼看出来
3n+1
2007a2007
1、4,7,10,13,16,19,…….,第n项为 _______.
2、a,-2a2,3a3,-4a4,5a5,-6a6,……. ,第2007项为________.
3、 , , , ……,第n项为_______.
1
3
1
5
1
7
1
9
1
2n+1
用火柴棒按以下方式搭小鱼
搭n条这样的小鱼需要多少根火柴棒?与同学交流。
搭20条这样的小鱼需要多少根火柴棒?
搭100条呢?
搭1条小鱼用___根火柴棒,搭2条小鱼用__根,搭3条小鱼用___根……每多搭1条小鱼增加___根火柴棒,搭n条小鱼需要____________根火柴棒。
8
14
20
6
[8+6(n-1)]
4
7
10
13
3n+1
……
火柴根数
4
3
2
1
正方形个数
例4、搭一搭,填一填:
(1)我们按如图的摆法搭一行正方形。记录你所搭的正方形的个数和所用的火柴棒的根数,并填表:
n
……
引题:
如图:工地上有一堆圆形钢管,第一层有2根,第二层3根,第三层4根,……
你能说出从第一层到第八层共有多少根吗?到第n层共有多少根呢?
……
解:当 n=8时,共有8×(8+3) ÷2=44根
n(n+3)
2
按下图方式摆放餐桌和椅子:
(1)1张餐桌可坐6人,2张餐桌可 人。
(2)按照上图的方式继续排列餐桌,完成下表:
桌子张数 3 4 5 6 ……
可坐人数
4+4
+4+2
4+4
+4+4+2
4+4+4+4+4+2
4+4+4
+4+4+4+2
4+4+2
……
(3)探索餐桌张数n与可坐人数w之间的关系。
W=4n+2
(4) 15张餐桌这样排,可坐多少人?
解:当n= 15时,w=4×15+2=62
别忘了
验证!
10
14
18
22
26
若按下图方式将桌子拼在一起。
(1)2张桌子拼在一起可坐 人,3张桌子可坐 人,n张桌子可坐 人。
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐 人;
(3)在(2)中,若改成每8张桌子拼成1张大桌子,则共可坐 人。
2×2+4
2n+4
112
100
2×3+4
练习:某种药品的数量与总价关系如下表:
写出药品数量x(克)与总价y(元)之间的关系。
y=2x+0.1
数量(克) 总价(元)
1 2.1
2 4.1
3 6.1
4 8.1
…… ……
=2+0.1
=4+0.1
=6+0.1
=8+0.1
1、你能搭出其他图形吗?并解决类似的问题?
课堂检测
n个三角形呢?
n层 呢?
2、下面的图形是由边长为1的正方形按照某种规律排列而组成的.
(1)观察图形,填写下表:
图形 ① ② ③
正方形的个数 8
(2)推测第n个图形中,正方形的个数为________ (用含n的代数式表示).
13
18
3、观察下面一列数:1,2,3,4,5,6,7,...,将这列数排成下列形式:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
… … … … … … … … … … …
按照上述规律排下去,那么第10行从左边第9个数是_______.
游戏规则 第一位同学将拿到的数字乘以2传给第二位同学,第二位同学将拿到的数加上3传给第三位同学,第三位同学将得到的数平方后传给第四位同学,第四位同学把结果减去5后传给第五位同学,第五位同学迅速将结果写在黑板上。
x
2x
2x+3
(2x+3)
(2x+3) -5
游戏
用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值。
例1.当a=3,b= -1时,求下列各代数式的值。
(1)(a+b) , (2) a +2ab+b , (3) (a-b) ,
(4) a -2ab+b
解:(1)当a=3,b= -1时,
(a+b) =[3+ (-1 )] =
(2)当a=3,b= -1时,
a +2ab+b =3 +2×3× (-1)+(-1)
=9+(-6)+1=
2 =4
4
(1)格式: “ 当 …… 时 ”
(2)代入时,数字要代入对应的字母的位置去;
(3)在求值时,原来省略的乘号要添上
( 4 )若代入 的是负数或分数,必须加上括号。
在我们求“代数式的值”时,有哪些是需要我们注意的呢?
解:(1)当a=3,b= -1时,
(a+b) =[3+(-1)] = 2 =4
(2)当a=3,b= -1时,
a +2ab+b =3 +2×3× (-1)+(-1)
=9+(-6)+1= 4
按右边图示的程序计算,若开始输入的n值为3,则最后输出的结果是 。
231
输入n
计算 的值
>200
输出结果
yes
no
你读懂了吗
挑战自我
1.若a+b=-1,求代数式
(1)a+b+2;
(2)3a+3b的值.
相同的代数式可以看作一个整体——整体代换.
解:∵a+b=-1
∴a+b+2=(-1)+2=1
解:∵a+b=-1
∴3a+3b+2=3(a+b)+2=3x(-1)+2
=-1
整体带入法
例1、若 的值为7,求代数式 的值。
解:由已知 ,则
=3 +4
(逆用乘法分配律)
例2、若2b-a=5,求代数式5(a-2b)2-3(a-2b)-60的值。
解:∵2b-a=5,∴a-2b=-5
∴ 5(a-2b)2-3(a-2b)-60=5×(-5)2-3×(-5)-60
=125+15-60
=80
1.代数式
挑战你自己
|x| - 5
________
x
中,x不能取的值是____;
x
_________
|x| - 5
中,x不能取得值是_____________.
0
+5与-5
2.已知x+y=5,求2(x+y) - ——— - (x+y)+1的值为 _________
10
x+y
44
4(a-b)
a+b
a+b
a-b
3.已知 ——
a-b
a+b
=3,则代数式 —— - —— 的
值为________
5
3
——
练习:
(1)若 ,则 ;
(2) 若 ,则 ;
(3) 若 ,则 ;
24
15
8
(4) 若 ,则 。
小结
1、求代数式的值的步骤:(1)写出字母的值,(2)代入,(3)计算;
2、求代数式的值的注意事项:
(1)代入数值前应先指明字母的取值,把“当……时”写出来。
(2)如果字母的值是负数、分数,并且要计算它的乘方,代入时应加上括号;
(3)代数式中省略了乘号时,代入数值以后必须添上乘号。
3、相同的代数式可以看作一个字母——整体代换。
4、代数式的值的广泛应用:计算机编程(包括用Excel处理数据等)、经济、生活等方面的应用。
试一试
1.若梯形的上底为a,下底为b,高为h,则
梯形的面积为_______________,
当a=2cm,b=3cm,h=4cm时,
s梯=____________.
S梯=
(a+b)h
10cm
2.测得某弹簧的长度y(厘米)与挂重x(千克)有下表关系(该弹簧挂重不得超过20千克):
X(千克) 0 1 2 3 ……
Y(厘米) 4 4.2 4.4 4.6 ……
(1)写出y与x的关系式:
(2)计算当弹簧的长度为5.6厘米的弹簧挂重.
3. 已知 ,求代数式
的值.
试一试
课后思考
若a2=1,则3a2=______
变式一:若a2+a=1,则3(a2+a)=______
变式二:若a2+a=1,则3a2+3a-5=______
变式三:若a2+a+3=0,则3a2+3a-5=______
1、今天星期五,再过100天星期几?
2、比较大小:
挑战自我,极限冲刺:
愿同学们越来越
聪明
不畏艰险,迎难而上!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
