21.3 实际问题与一元二次方程课件(共80张PPT)2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 21.3 实际问题与一元二次方程课件(共80张PPT)2025-2026学年数学人教版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:24:08 | ||
图片预览








文档简介
(共80张PPT)
第二十一章 一元二次方程
第一单元
21.3 实际问题与一元二次方程
第一课时 传播问题和变化率问题
1.根据实际问题中的数量关系,正确列出一元二次方程。
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识。
复习巩固
探究新知
典例分析
针对训练
探究新知
典例分析
针对训练
归纳小结
直击中考
布置作业
【提问】已经学过了哪些解一元二次方程的方法
x2=a (a≥0)
(x+m)2=n (n≥0)
直接开方法
配方法
公式法
因式分解法
(x-x1)(x-x2)=0
【提问】回顾列方程解决实际问题的基本步骤
1)审:分清已知未知,明确数量关系;
2)设:设未知数;
3)列:列方程;
4)解:解方程;
5)验:根据实际验结果;
6) 答:写出答案。
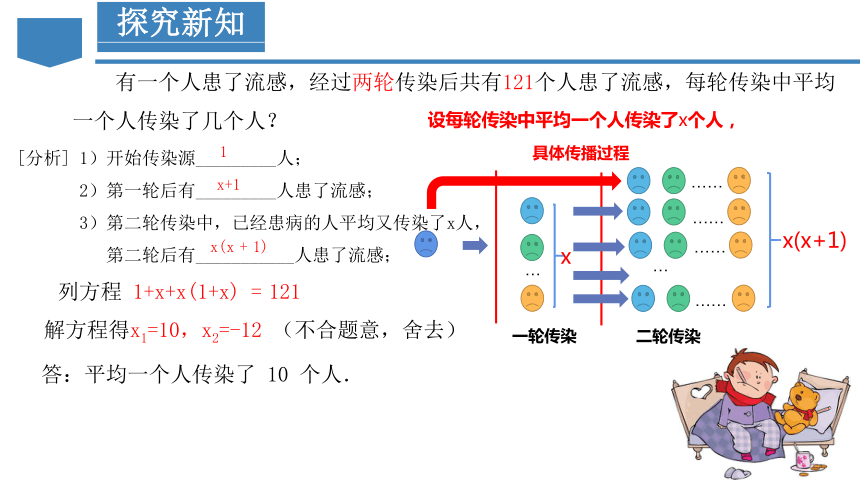
有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
[分析] 1)开始传染源_________人;
2)第一轮后有_________人患了流感;
3)第二轮传染中,已经患病的人平均又传染了x人,
第二轮后有___________人患了流感;
x+1
x(x + 1)
1
设每轮传染中平均一个人传染了x个人,
一轮传染
二轮传染
具体传播过程
…
……
……
……
……
…
x
x(x+1)
列方程 1+x+x(1+x) = 121
答:平均一个人传染了 10 个人.
解方程得x1=10,x2=-12 (不合题意,舍去)
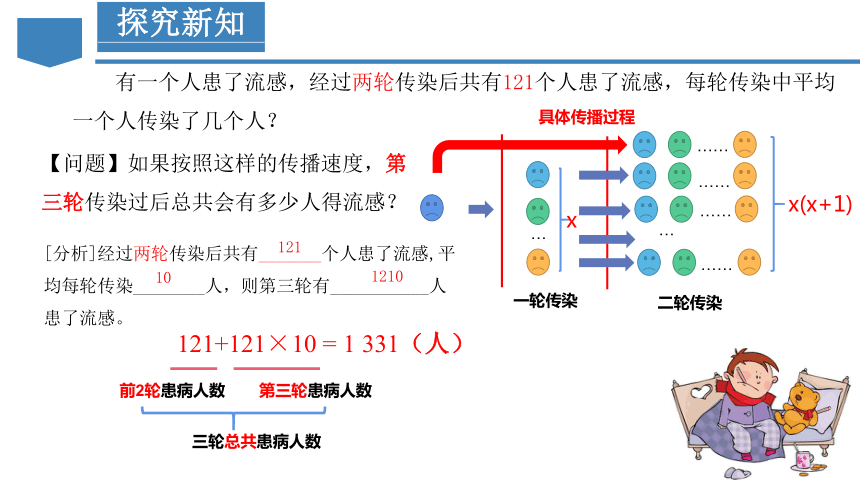
有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
一轮传染
二轮传染
具体传播过程
…
……
……
……
……
…
x
x(x+1)
【问题】如果按照这样的传播速度,第三轮传染过后总共会有多少人得流感?
[分析]经过两轮传染后共有_______个人患了流感,平均每轮传染________人,则第三轮有___________人患了流感。
121
10
1210
121+121×10 = 1 331(人)
前2轮患病人数
第三轮患病人数
三轮总共患病人数
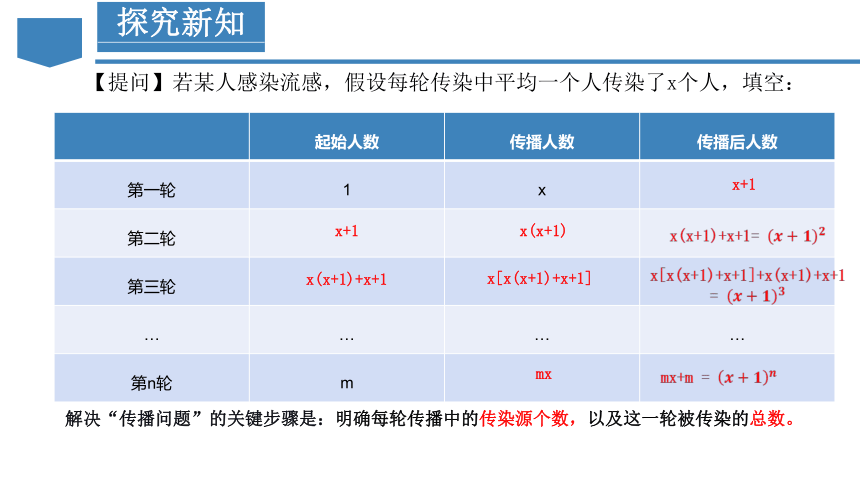
【提问】若某人感染流感,假设每轮传染中平均一个人传染了x个人,填空:
起始人数 传播人数 传播后人数
第一轮 1 x
第二轮
第三轮
… … … …
第n轮 m
x+1
x+1
x(x+1)
x(x+1)+x+1=
x(x+1)+x+1
x[x(x+1)+x+1]
x[x(x+1)+x+1]+x(x+1)+x+1
=
mx
mx+m =
解决“传播问题”的关键步骤是:明确每轮传播中的传染源个数,以及这一轮被传染的总数。
【详解】
解:设每轮感染中平均一台电脑会感染x台电脑,
由题可知,
整理得,
解得,(舍),
则(1+x)2+x(1+x)2=(1+x)3=(1+11)3=1728>1700.
答:每轮感染中平均一台电脑会感染11台电脑.若病毒得不到有效控制,3轮感染后,被感染的电脑会超过1700台;
例1 某种电脑病毒传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有144台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过1700台?
【解析】
(1)解:由题意可知:第一轮传染后患病的人数人,
(2)解:设在每轮传染中一人将平均传给人,
根据题意得:,
整理得:,
解得:,,
∵,都不是正整数,
∴第二轮传染后共会有21人患病的情况不会发生.
例2 某种流感病毒,若有一人患了这种流感,则在每轮传染中一人将平均传染x人.
(1)现有一人患上这种流感,求第一轮传染后患病的人数(用含x的代数式表示);
(2)在进入第二轮传染前,有两位患者被及时隔离并治愈,问第二轮传染后患病的人数会有21人吗?
【详解】(1)解:第一轮被感染的人数为x,第二轮被传染上流感人数是,
(2)解:经过两轮传染后不会有63人患病的情况发生,理由如下:
依题意得:,
整理得:,
解得:,(不合题意,舍去),
∵不为正整数,
∴第二轮传染后不会有63人患病的情况发生.
1.有一个人患了流感,经过两轮传染后有若干人被传染上流感.假设在每轮的传染中平均一个人传染了x个人.
(1)第二轮被传染上流感人数是______;(用含x的代数式表示)
(2)在进入第二轮传染之前,如果有4名患者被及时隔离(未治愈),经过两轮传染后是否会有63人患病的情况发生,并说明理由.
【详解】解:(1) (场),答:共进行6场比赛;
(2)设有 支球队参加比赛,根据题意得: ,
解得: (不合题意,舍去),
答:有9支球队参加比赛.
2. 学生会要组织“西实杯”篮球赛,赛制为单循环形式(每两队之间都赛一场).
(1)如果有4支球队参加比赛,那么共进行______场比赛;
(2)如果全校一共进行36场比赛,那么有多少支球队参加比赛?
3 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少个小分支?
假设每个支干长出2枝
1+2+=7
假设每个支干长出3枝
1+3+=13
假设每个支干长出n枝
1+n+
3 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少个小分支?
解:设每个支干长出 x 个小分支,
则 1 + x + x2 = 91
解方程,得x1 = 9,x2 = -10(不合题意,舍去)
答:每个支干长出 9 个小分支
1.某农户的小麦产量年平均增长率为 x,第一年的产量为 50 000 kg,第二年的产量为____________ kg,第三年的产量为______________ kg.
50 000(1 + x )
2.某粮食厂2021年面粉产量为a吨,如果在以后两年平均减产的百分率为 x,那么预计 2022年的产量将是_________吨.2023年的产量将是__________吨.
a(1–x)
年平均增长率为 x
50000
50 000(1 + x )
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
【提问】什么是下降额?下降率如何计算?
下降额=下降前的量-下降后的量
增长额=增长后的量-增长前的量
下降率= =
【提问】什么是增长额?增长率如何计算?
增长率= =
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
乙种药品成本的年平均下降额为(6000-3600)÷2=1200(元).
甲种药品成本的年平均下降额为(5000-3000)÷2=1000(元),
显然,乙种药品的年平均下降额较大,但是年平均下降额(元)不等同于年平均下降率(百分率)。
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
解:设甲种药品成本的年平均下降率为 x
一年后甲种药品成本为____________元,
两年后甲种药品成本为____________元.
列方程得=3000
解方程得 x1≈0.225,x2≈1.775(舍去).
答:甲种药品成本的年平均下降率为22.5%
-x)
【补充】下降率是用减少的数除以原数,则所得结果必定小于1,因此不能大于或等于1。
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
解:设乙种药品成本的年平均下降率为 y
一年后乙种药品成本为____________元,
两年后乙种药品成本为____________元.
列方程得=3600
解方程得 x1≈0.225,x2≈1.775(舍去).
答:乙种药品成本的年平均下降率为22.5%
1-y)
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
【问题】经过计算,你能得出什么结论?
【问题】成本下降额大的药品,它的成本下降率一定也大吗?
【问题】应怎样全面地比较几个对象的变化状况?
成本下降额表示绝对变化量,
成本下降率表示相对变化量,
两者兼顾才能全面比较对象的变化状况。
两种药品成本的年平均下降率相等
成本下降额较大的产品,其成本下降率不一定较大。
【详解】(1)设每个月生产成本的下降率为x,
根据题意得:400(1﹣x)2=361,
解得:x1=0.05=5%,x2=1.95(不合题意,舍去).
答:每个月生产成本的下降率为5%;
(2)361×(1﹣5%)=342.95(万元),
答:预测4月份该公司的生产成本为342.95万元.
例3 某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司2、3、4月每个月生产成本的下降率都相同.
(1)求每个月生产成本的下降率;
(2)请你预测4月份该公司的生产成本.
【详解】(1)解:设这两个月参观人数的月平均增长率为,
由题意得:,
解得:,(不合题意,舍去),
答:这两个月参观人数的月平均增长率为.
(2)(万人),
答:六月份的参观人数为13.31万人.
1.2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.
(1)求这两个月参观人数的月平均增长率;
(2)按照这个增长率,预计6月份的参观人数是多少?
1.2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,共有多少支队伍参加比赛?( )
A.8 B.10 C.7 D.9
2.某县年人均可支配收入为万元,年达到万元,若年至年间每年人均可支配收入的增长率都为,则下面所列方程正确的是( )
A. B.
C. D.
【详解】设有x支队伍,根据题意,得,解方程,得x1=10,x2=-9(舍去),故选B.
【详解】解:设年至年间每年人均可支配收入的增长率都为,根据题意得,
,故选:B.
【详解】
第一个月新建了301个充电桩,该市新建智能充电桩个数的月平均增长率为.
第二个月新建了个充电桩,
第三个月新建了个充电桩,
第三个月新建了500个充电桩,于是有,
故答案为.
3.为了加快数字化城市建设,某市计划新建一批智能充电桩,第一个月新建了301个充电桩,第三个月新建了500个充电桩,设该市新建智能充电桩个数的月平均增长率为,根据题意,请列出方程________.
【详解】(1)解:设这两个月中该景区游客人数的月平均增长率为,
由题意,得:,解得:(负值已舍掉);
答:这两个月中该景区游客人数的月平均增长率为;
(2)设5月份后10天日均接待游客人数是y万人,
由题意,得:,解得:;
∴5月份后10天日均接待游客人数最多是1万人.
4.随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.
(1)求这两个月中该景区游客人数的月平均增长率;
(2)预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?
【详解】
解:(1)设亩产量的平均增长率为x,
根据题意得:, 解得:,(舍去),
答:亩产量的平均增长率为20%.
(2)第四阶段的亩产量为(公斤),
∵,∴他们的目标可以实现.
5.“杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.
1. 本节课学习,你有哪些收获?请你用自己的语言简述一元二次方程解应用题的步骤?
2. 你知道本节课研究“传播问题”的基本特征吗?解决此类问题的关键步骤是什么?
“传播问题”的基本特征:以相同的速度逐轮传播。
解决此类问题的关键步骤:明确每轮传播中的传染源个数,以及这一轮被传染的总数。
第二十一章 一元二次方程
第一单元
21.3 实际问题与一元二次方程
第二课时 几何问题和数字问题
1.根据实际问题中的数量关系,正确列出一元二次方程。
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识。
复习巩固
探究新知
典例分析
针对训练
归纳小结
探究新知
典例分析
归纳小结
直击中考
布置作业
针对训练
【提问】回顾列方程解决实际问题的基本步骤
1)审:分清已知未知,明确数量关系;
2)设:设未知数;
3)列:列方程;
4)解:解方程;
5)验:根据实际验结果;
6) 答:写出答案。
【提问】计算下列图形面积
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
【分析】封面的长宽之比是9∶7,中央的矩形的长宽之比也应是9∶7。
设中央的矩形的长和宽分别是 9a cm和 7a cm,由此得上、下边衬与左、右边衬的宽度之比是:
9a
7a
(27-9a): (21-7a)= 9(3-a):7(3-a)= 9:7
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
解法一:设上、下边衬的宽均为9y cm ,左、右边衬的宽均为7y cm,
由题意得 (27-18y)(21-14y)=27
整理,得:16y 2 - 48y + 9 = 0
解方程,得y=
则y1=舍去)
答:上、下边衬的宽度为1.8cm,左、右边衬的宽度为1.4cm
所以9y=1.8 cm,7y=1.4 cm
【提问】为什么舍去2.8?请说明原因?
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
解法二:设正中央的矩形长和宽分别为9x cm,7x cm
由题意得 927
解方程,得x=
则x1=舍去)
答:上、下边衬的宽度为1.8cm,左、右边衬的宽度为1.4cm
故上、下边衬的宽度为≈1.8 cm,
左、右边衬的宽度为≈1.4 cm
如图,在一块长为 92m ,宽为 60m 的矩形耕地上挖三条水渠,水渠的宽都相等,水渠
把耕地分成面积均为 885m2 的 6 个小矩形,水渠应挖多宽?
【分析】设水渠宽为 x m,将所有耕地的面积拼在一起,变成一个新的矩形,它的长为 ___________m, 宽___________m.
60
92
60-x
92-2x
(92 – 2x )
(60-x)
解:设水渠的宽应挖 x m .
( 92 - 2x)(60 - x )= 6×885
解得 x1=105(舍去),x2=1
答:水渠应挖1米宽
如图,在一块长为 92m ,宽为 60m 的矩形耕地上挖三条水渠,水渠的宽都相等,水渠
把耕地分成面积均为 885m2 的 6 个小矩形,水渠应挖多宽?
【分析】设水渠宽为 x m,水渠的总面积为______________________________________________
92x
+260x
-2x2
解:设水渠的宽应挖 x m .
92×60 - 92x - 2×60x+ 2x2 = 6×885
解得 x1=105(舍去),x2=1
答:水渠应挖1米宽
例1 等腰梯形的面积为160cm2,上底比高多4cm,下底比上底多16cm,求这个梯形的高。
解:设这个梯形的高为 x cm,则上底为(x+4)cm,下底为(x+20)cm.
根据题意得(x+4+x+20)=160
整理,得x2 +12x -160= 0
解得 x1=8 , x2=-20 ( 不合题意,舍去 )
答:这个梯形的高为8cm.
1.如图,准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路,四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为_____米.
【详解】
设小路的宽度为,由题意得,由,可得.
2. 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,若墙长为18m,另三边用竹篱笆围成,篱笆总长35m,围成长方形的养鸡场四周不能有空隙.
(1)要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由.
【详解】
解:1)设养鸡场的宽为xm,根据题意得:x(35﹣2x)=150,
解得:x1=10,x2=7.5,
当x1=10时,35﹣2x=15<18,
当x2=7.5时35﹣2x=20>18,(舍去),
则养鸡场的宽是10m,长为15m.
2. 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,若墙长为18m,另三边用竹篱笆围成,篱笆总长35m,围成长方形的养鸡场四周不能有空隙.
(1)要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由.
【详解】
2)设养鸡场的宽为xm,根据题意得:x(35﹣2x)=200,
整理得:2x2﹣35x+200=0,
△=(﹣35)2﹣4×2×200=1225﹣1600=﹣375<0,
因为方程没有实数根,所以围成养鸡场的面积不能达到200m2.
几何问题
与一元二次方程
几何图形
常见几何图形周长或面积是等量关系.
类 型
课本封面问题
小路宽度问题
常采用图形平移,聚零为整方便列方程.
通过列方程式,算出周瑜去世时的年龄。
将题干内容转换为数学语言:
周瑜三十岁当东吴都督,去世时的年龄是两位数,十位数字比个位数字小三,个位数字的平方等于他去世时的年龄。
【详解】解:设周瑜去世时的年龄的个位数字为,则十位数字为,依题意得:
,
解得,,
当时,,(不合题意,舍去),
当时,(符合题意),
答:周瑜去世时的年龄为岁.
一个两位数的个位数字与十位数字的和为9,并且个位数字与十位数字的平方和为45,求这个两位数.
【详解】设个位数字为,则十位数字为.
得,
∴这个两位数为36或63.
【详解】设一位数为,则两位数为.
则根据题意可得:,
整理得:.
分解得:,
解得:,.
答:这个两位数为16或49.
典例2 一个两位数是一个一位数的平方,把这个一位数放在这个两位数的左边所成的三位数,比把这个一位数放在这个两位数的右边所成的三位数大,求这个两位数.
【详解】设其中较小的奇数为,则较大的奇数为,
根据题意,得,
解得,
当时,;
当时,.
故答案为:,或.
1 两个连续奇数的积为,若设其中较小的奇数为,则可列方程为_________________,这两个数分别为_______________.
1.第十四届国际数学教育大会(ICME—14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745,八进制是以8作为进位基数的数字系统,有0~7共8个基本数字,八进制数3745换算成十进制数是,表示ICME—14的举办年份.
(1)八进制数3747换算成十进制数是______;
(2)小华设计了一个n进制数234,换算成十进制数是193,求n的值.
【详解】(1)
(2)由题意,得,
解得,(舍负)
2 阅读材料,回答下列问题:
反序数:有这样一对数,一个数的数字排列完全颠倒过来变成另一个数,简单的说,就是顺序相反的两个数,我们把这样的一对数称为“反序数”,比如:的反序数是,的反序数是.
用方程知识解决问题:若一个两位数,其十位上的数字比个位上的数字大3,这个两位数与其反序数之积为,求这个两位数.
【详解】解:设这个两位数的个位数字为x,则十位数字为,
根据题意得:,
∴,即,
∴,
∴
解得x=2或(舍去),
∴,
∴这个两位数为.
3 如图,某中学课外兴题小组准备围建一个矩形花园 ABCD,其中一边靠墙,另外三边用总长为60 m的篱笆围成,与墙平行的一边 BC上要预留2 m宽的入口(如图中MN所示,不用篱笆),已知墙长为 28 m.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成500平方米的矩形花园 若能求出 BC长;若不能,说明理由.
【详解】(1)设矩形花园BC的长为x米,则其宽为(60﹣x+2)米,
依题意列方程得:(60﹣x+2)x=300,
解这个方程得:x1=12,x2=50,
∵28<50,∴x2=50(不合题意,舍去),
∴x=12.
答:当矩形的长BC为12米时,矩形花园的面积为300平方米;
3 如图,某中学课外兴题小组准备围建一个矩形花园 ABCD,其中一边靠墙,另外三边用总长为60 m的篱笆围成,与墙平行的一边 BC上要预留2 m宽的入口(如图中MN所示,不用篱笆),已知墙长为 28 m.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成500平方米的矩形花园 若能求出 BC长;若不能,说明理由.
(2)设矩形花园BC的长为x米,则其宽为(60﹣x+2)米,依题意列方程得:(60﹣x+2)x=500,
△=622﹣4000=﹣156<0,
则该方程无解,即不能围成500平方米的矩形花园.
答:不能围成500平方米的矩形花园.
1.如图,在长为50m,宽为38m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为1260m2,道路的宽应为多少?
【详解】解:设道路的宽应为x米,
由题意得 (50-2x)×(38-2x)=1260
解得:x1=4,x2=40(不符合题意,舍去)
答:道路的宽应为4m.
【详解】解:设这个最小数为.
根据题意,得x(x+8)=65.
解得,(不符合题意,舍去).
答:这个最小数为5.
2.2021年7日1日建党100周年纪念日,在本月日历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为65,求这个最小数(请用方程知识解答).
1. 本节课学习,你有哪些收获?请你用自己的语言简述一元二次方程解应用题的步骤?
2. 你知道解决“几何问题” 、“数字问题” 的关键步骤是什么?
第二十一章 一元二次方程
第一单元
21.3 实际问题与一元二次方程
第三课时 销售问题、图表问题、动点问题
1.根据实际问题中的数量关系,正确列出一元二次方程。
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识。
复习巩固
探究新知
典例分析
针对训练
探究新知
典例分析
针对训练
归纳小结
直击中考
布置作业
探究新知
典例分析
针对训练
【提问】回顾列方程解决实际问题的基本步骤
1)审:分清已知未知,明确数量关系;
2)设:设未知数;
3)列:列方程;
4)解:解方程;
5)验:根据实际验结果;
6) 答:写出答案。
九年级学生小明在暑假期间勤工俭学。
1)他每天在批发市场以每斤2.5元买进黄瓜,再到市场以每斤4元卖掉黄瓜,那么他每卖1斤黄瓜可以赚到 元;
2)如果他每天都能卖完50斤黄瓜,则他每天收入是 元。
3)他每天外面吃饭需花费20元,则他每天实际可以获得_____________元。
1.5
75
单件售价-单件进价=单件利润
单件利润×销量=总利润
50
总利润-支出=实际利润(或:销售总额-成本总额-支出=实际利润)
【提问】根据上述问题,你能售价、进价、利润、支出之间存在的关系吗
[补充]1)利润率=100% 2)商品售价=标价
3)商品售价=商品进价(1+利润率)
某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减小库存,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1200元,那么衬衫的单价降了多少元?
【分析】设衬衫单价应降x元,
单件利润 销量 总利润
降价前
降价后
40-x
20+2x
设衬衫单价应降x元
由题意得(40-x)(20+2x)=1200
解方程得x1=20,x2=10
【提问】站在商家角度你觉得如何降价合适?
40
20
800
1200
∵尽快减小库存∴ x=20
答:衬衫的单价降了20元
某商店进了一批服装,进货单价为50元,若按每件60元出售,则可销售800件;若每件再提价1元出售,则其销售量就减少20件。现在预算要获利润12000元且进货成本不超过24000元,应按每件多少元出售?
【分析】设应按每件 x 元出售
进价 售价 单件利润 销量 总利润
提价前 50 60 10 800 8000
提价后 50
x
x-50
800-20(x-60)
12000
设应按每件 x 元出售
由题意得(x-50)[ 800-20(x-60)]=12000
解方程得x1=70,x2=80
当x=70时,50 (800-20 10)=30000>24000 舍去
当x=80时,50 (800-20 20)=20000<24000
答:应按每件 80 元出售,进货数量400件
某商店进了一批服装,进货单价为50元,若按每件60元出售,则可销售800件;若每件再提价1元出售,则其销售量就减少20件。现在预算要获利润12000元且进货成本不超过24000元,应按每件多少元出售?
【提问】如果设提价x元,你能根据提示信息列出方程吗?
设提价x元
由题意得(10+x)(800-20x)=12000
解方程得x1=10,x2=20
当x=10时,50 (800-20 10)=30000>24000 舍去
当x=20时,50 (800-20 20)=20000<24000
当x=20时,60+x=60+20=80 元
答:应按每件 80 元出售,进货数量400件
例1 某工厂生产的某种产品按供需要求分为十个档次.若生产第一档次(最低档次)的产品,一天可生产76件,每件的利润为10元,每提高一个档次,每件的利润增加2元,每天的产量将减少4件.设该产品的档次(每天只生产一个档次的产品)为x,请解答下列问题.
1)用含x的代数式表示:一天生产的产品件数为_______件,每件产品的利润为________元;
档次 销售量(件) 单件利润(元)
1(最低) 76 10
2
3
4
... ... ...
10(最高)
x
12
72
14
68
16
64
28
40
10+2(x-1)
76-4(x-1)
解(1)一天生产的产品件数为[76-4(x-1)]=(80-4x)件,
每件产品的利润为[10+2(x-1)]=(8+2x)元,
例1 某工厂生产的某种产品按供需要求分为十个档次.若生产第一档次(最低档次)的产品,一天可生产76件,每件的利润为10元,每提高一个档次,每件的利润增加2元,每天的产量将减少4件.设产品的档次(每天只生产一个档次的产品)为x,请解答下列问题.
2)若该产品一天的总利润为1080元,求这天生产产品的档次x的值.
(2)当利润是1080元时,即:[10+2(x-1)][76-4(x-1)]=1080,
整理得:-8x2+128x+640=1080,
解得:x1=5,x2=11,
∵x=11>10,不符合题意,舍去。∴x=5,
答:当生产产品的质量档次是在第5档次时,一天的总利润为1080元。
【详解】解:设每副羽毛球拍降价x元,
由题意得:(40-x)(20+5x)=1700,
整理得:x2-36x+180=0,
解方程得:x1=6,x2=30,
因为 每副降价幅度不超过15元,
所以 x=6符合题意,故答案是:6.
1.李华在网上开了一家羽毛球拍专卖店,平均每天可销售副,每个盈利元,若每副降价元,则每天可多销售副.如果每天要盈利元,每副应降价______元(要求每个降价幅度不超过元)
【详解】解:1)设每千克核桃应降价x元
根据题意,得(60﹣x﹣40)(100+×20)=2240,
化简,得 x2﹣10x+24=0,
解得x1=4,x2=6.
答:每千克核桃应降价4元或6元.
2.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
1)每千克核桃应降价多少元?
2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
2)由1)可知每千克核桃可降价4元或6元.
∵要尽可能让利于顾客,
∴每千克核桃应降价6元
此时,售价为:60﹣6=54(元),
答:该店应按原售价的九折出售.
2.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
1)每千克核桃应降价多少元?
2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
某公司组织一批员工到龙湾风景区旅游,支付给旅行社28000元,你能确定参加这次旅游的人数吗?
解:设参加旅游人数共有x人,
∵800×30=24000<28000,∴参加人数x>30,
根据题意,得x× [800-10(x-30)]=28000.
整理,得
解得,x1=40,x2=70
当x=40时, [800-10(x-30)]=800-10 (40-30)=700>500
当x=70时, [800-10(x-30)]=800-10 (70-30)=400<500(不符合题意,舍去)
答:参加人数共有40人
【分析】设参加旅游人数共有x人,公司支付给旅行社28000元,说明__________,则人均收费__________________________元
x>30
[800-10(x-30)]
为了节约用水,某水厂规定:某单元居民如果一个月的用水量不超过吨,那么这个月该单元居民只交10元水费.如果超过吨,则这个月除了仍要交10元水费外,超过那部分按每吨元交费.
1)该单元居民8月份用水80吨,超过了“规定的吨”,则超过部分应交水费 元(用含x的式子表示).
2)下表是该单元居民9月、10月的用水情况和交费情况:
根据上表数据,求该x吨是多少?
月份 用水量(吨) 交费总数(元)
9月份 85 25
10月份 50 10
【详解】
解:(1)超过的用水量为(80-x)吨,所以,超过部分应交水费(80-x)元;
(2)根据表格提供的数据,可以知道,根据9月份用水情况可以列出方程:(85-x)=25
解得,x1=60,x2=25
因为,所以x=60
答:该水厂规定的x吨是60吨.
例2 某市出租车收费标准如下(规定:四舍五入,精确到元,N≤15)N是走步价,李先生乘坐出租车打出的电子收费单是:里程11公里,应收29.1元,你能依据以上信息,推算出起步价N的值吗
里程x(km) 0<x≤3 3<x≤6 x>6
单价y(元) N
【详解】
由题意,可列出方程
整理得N2—29.1N+191=0.
解方程得N1=10,N2=19.1(不合题意舍去)
答:起步价是10元.
某公司组织一批员工到该风景区旅游,支付给旅行社2800元.A公司参加这次旅游的员工有多少人?某风景区的旅游信息如下:
旅游人数 收费标准
不超过30人 人均收费80元
超过30人 每增加1人,人均收费降低1元,但人均收费不低于55元
设参加这次旅游的员工有x人,
∵30×80=2400<2800,∴x>30.
根据题意得:x[80-(x-30)]=2800,
解得:x1=40,x2=70.
当x=40时,80-(x-30)=70>55,
当x=70时,80-(x-30)=40<55,舍去.
答:A公司参加这次旅游的员工有40人.
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动.几秒钟后△DPQ的面积等于28cm2?
A
B
C
D
P
Q
【提示】设x s后△DPQ的面积等于28cm2,则AP、PB、BQ、QC的长度分别可用含x的代数式表示,从而Rt △DAP 、 Rt △PBQ、 Rt △QCD的面积也都可以用含x的代数式表示,于是可以列出方程。
x
6
12
12-2x
2x
6-x
设x s后△DPQ的面积等于28cm2,则S△APD =______________
S△PBQ =________________, S△DCQ =_________________
根据题意得,
+ +28=72
化简得,
解方程得, x1=2,x2=4
答:2s或4s后△DPQ的面积等于28cm2
例3 如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C出发,点P以3cm/s的速度向点B移动,一直到达B为止;点Q以2cm/s的速度向点D移动。经过多长时间P、Q两点之间的距离是10cm?
设经过x s时间P、Q两点之间的距离是10cm。
3x
2x
2x
16-5x
解方程得x1=1.6,x2=4.8
答:1.6s或4.8s后P、Q距离是10cm
3x
2x
2x
16-5x
E
x=2时,由运动可知AP=3×2=6 cm,CQ=2×2=4 cm,
∴四边形ABCD是矩形,
∴QE=AD=6,
∴PE=AB﹣BE﹣AP=16﹣6﹣4=6,
根据勾股定理得PQ=,
∴当x=2 s时,P,Q两点的距离为6 cm;
2x
如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C出发,点P以3cm/s的速度向点B移动,一直到达B为止;点Q以2cm/s的速度向点D移动。
1)当运动时间为2s时,P,Q两点的距离为多少?
2)当运动时间为4s时,P,Q两点的距离为多少?
P’
x=4时,由运动知AP′=3×4=12 cm,CQ′=2×4=8 cm,
∴四边形ABCD是矩形,
∴P′E=AD=6,
P′B=CE=AB-AP′=16-12=4
∴Q′E=Q′C﹣CE=8﹣4=4,
根据勾股定理得P′Q′=,
∴当x=4 s时,P,Q两点的距离为cm;
Q’
E
如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C出发,点P以3cm/s的速度向点B移动,一直到达B为止;点Q以2cm/s的速度向点D移动。
1)当运动时间为2s时,P,Q两点的距离为多少?
2)当运动时间为4s时,P,Q两点的距离为多少?
【详解】解:(1)设与销售单价之间的函数关系式为:y=kx+b,
将点(1,110)、(3,130)代入一次函数表达式得:
,解得:,故函数的表达式为:y=10x+100;
(2)由题意得:(10x+100)(55-x-35)=1760,
整理,得.
解得,(舍去).所以55-x=43.
答:这种消毒液每桶实际售价43元.
1.某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量(桶)与每桶降价(元)()之间满足一次函数关系,其图象如图所示:
(1)求与之间的函数关系式;
(2)在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?
【详解】(1)若降价3元,则平均每天销售数量为20+2×3=26件.
(2)设每件商品应降价x元时,该商店每天销售利润为1200元.
根据题意,得(40-x)(20+2x)=1200,
解得:x1=10,x2=20.
∵要求每件盈利不少于25元,∴x2=20应舍去,∴x=10.
答:每件商品应降价10元时,该商店每天销售利润为1200元.
2.某商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为________件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
【详解】解:设该水果每千克降价x(x>0)元,
则每千克的利润为:元,销售量为:千克,
根据
或,
要尽可能让顾客得到实惠,
即售价为(元)
答:该水果的销售价为每千克29元.
3.端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求该水果的销售价为每千克多少元?
1. 本节课学习,你有哪些收获?请你用自己的语言简述一元二次方程解应用题的步骤?
2. 你知道解决“销售问题” 、“图表问题” 、“动点问题” 的关键步骤是什么?
1.某演出团体准备在苏州文化艺术中心大剧院举办迎新演出,该剧院有1200个座位,如果票价定为每张100元,那么门票可以全部售出如果票价每增加1元,那么门票就减少2张,要使得门票收入为245000元,票价应该定为多少元?
2.某超市销售一种矿泉水,进价为每箱24元,现在的售价为每箱36元,每月可销售60箱。经市场调查发现:若这种矿泉水的售价每降价1元,则每月的销量将增加10箱.如果该超市想要每月销售这种矿泉水的利润为650元,那么每箱矿泉水需要降价多少元?
3.如图,已知AB⊥BC,AB=12 cm,BC=8 cm.动点M从点A沿AB方向以2 cm/s的速度向点B运动,同时动点N从点C沿CB方向以1 cm/s的速度也向点B运动,其中一点到达B点时另一点也随之停止.当△MNB的面积为24 cm2时,求它们运动的时间.
1.解:设应定为x元,
则由题意可得:
即解得:
答:定价定为350元.
2.设每箱降价元,则每月可销售(10 +60)箱,
依题意得:(36 x 24)(10x+60)=650,
解得: (舍去).
答:每箱矿泉水需要降价7元.
3.解:根据题意可知cm, cm,
∴cm, cm,
∵△MNB的面积为24cm2,
∴,
解得:t1=2,t2=12(不合题意,舍去)
∴运动的时间为2s.
第二十一章 一元二次方程
第一单元
21.3 实际问题与一元二次方程
第一课时 传播问题和变化率问题
1.根据实际问题中的数量关系,正确列出一元二次方程。
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识。
复习巩固
探究新知
典例分析
针对训练
探究新知
典例分析
针对训练
归纳小结
直击中考
布置作业
【提问】已经学过了哪些解一元二次方程的方法
x2=a (a≥0)
(x+m)2=n (n≥0)
直接开方法
配方法
公式法
因式分解法
(x-x1)(x-x2)=0
【提问】回顾列方程解决实际问题的基本步骤
1)审:分清已知未知,明确数量关系;
2)设:设未知数;
3)列:列方程;
4)解:解方程;
5)验:根据实际验结果;
6) 答:写出答案。
有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
[分析] 1)开始传染源_________人;
2)第一轮后有_________人患了流感;
3)第二轮传染中,已经患病的人平均又传染了x人,
第二轮后有___________人患了流感;
x+1
x(x + 1)
1
设每轮传染中平均一个人传染了x个人,
一轮传染
二轮传染
具体传播过程
…
……
……
……
……
…
x
x(x+1)
列方程 1+x+x(1+x) = 121
答:平均一个人传染了 10 个人.
解方程得x1=10,x2=-12 (不合题意,舍去)
有一个人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
一轮传染
二轮传染
具体传播过程
…
……
……
……
……
…
x
x(x+1)
【问题】如果按照这样的传播速度,第三轮传染过后总共会有多少人得流感?
[分析]经过两轮传染后共有_______个人患了流感,平均每轮传染________人,则第三轮有___________人患了流感。
121
10
1210
121+121×10 = 1 331(人)
前2轮患病人数
第三轮患病人数
三轮总共患病人数
【提问】若某人感染流感,假设每轮传染中平均一个人传染了x个人,填空:
起始人数 传播人数 传播后人数
第一轮 1 x
第二轮
第三轮
… … … …
第n轮 m
x+1
x+1
x(x+1)
x(x+1)+x+1=
x(x+1)+x+1
x[x(x+1)+x+1]
x[x(x+1)+x+1]+x(x+1)+x+1
=
mx
mx+m =
解决“传播问题”的关键步骤是:明确每轮传播中的传染源个数,以及这一轮被传染的总数。
【详解】
解:设每轮感染中平均一台电脑会感染x台电脑,
由题可知,
整理得,
解得,(舍),
则(1+x)2+x(1+x)2=(1+x)3=(1+11)3=1728>1700.
答:每轮感染中平均一台电脑会感染11台电脑.若病毒得不到有效控制,3轮感染后,被感染的电脑会超过1700台;
例1 某种电脑病毒传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有144台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过1700台?
【解析】
(1)解:由题意可知:第一轮传染后患病的人数人,
(2)解:设在每轮传染中一人将平均传给人,
根据题意得:,
整理得:,
解得:,,
∵,都不是正整数,
∴第二轮传染后共会有21人患病的情况不会发生.
例2 某种流感病毒,若有一人患了这种流感,则在每轮传染中一人将平均传染x人.
(1)现有一人患上这种流感,求第一轮传染后患病的人数(用含x的代数式表示);
(2)在进入第二轮传染前,有两位患者被及时隔离并治愈,问第二轮传染后患病的人数会有21人吗?
【详解】(1)解:第一轮被感染的人数为x,第二轮被传染上流感人数是,
(2)解:经过两轮传染后不会有63人患病的情况发生,理由如下:
依题意得:,
整理得:,
解得:,(不合题意,舍去),
∵不为正整数,
∴第二轮传染后不会有63人患病的情况发生.
1.有一个人患了流感,经过两轮传染后有若干人被传染上流感.假设在每轮的传染中平均一个人传染了x个人.
(1)第二轮被传染上流感人数是______;(用含x的代数式表示)
(2)在进入第二轮传染之前,如果有4名患者被及时隔离(未治愈),经过两轮传染后是否会有63人患病的情况发生,并说明理由.
【详解】解:(1) (场),答:共进行6场比赛;
(2)设有 支球队参加比赛,根据题意得: ,
解得: (不合题意,舍去),
答:有9支球队参加比赛.
2. 学生会要组织“西实杯”篮球赛,赛制为单循环形式(每两队之间都赛一场).
(1)如果有4支球队参加比赛,那么共进行______场比赛;
(2)如果全校一共进行36场比赛,那么有多少支球队参加比赛?
3 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少个小分支?
假设每个支干长出2枝
1+2+=7
假设每个支干长出3枝
1+3+=13
假设每个支干长出n枝
1+n+
3 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少个小分支?
解:设每个支干长出 x 个小分支,
则 1 + x + x2 = 91
解方程,得x1 = 9,x2 = -10(不合题意,舍去)
答:每个支干长出 9 个小分支
1.某农户的小麦产量年平均增长率为 x,第一年的产量为 50 000 kg,第二年的产量为____________ kg,第三年的产量为______________ kg.
50 000(1 + x )
2.某粮食厂2021年面粉产量为a吨,如果在以后两年平均减产的百分率为 x,那么预计 2022年的产量将是_________吨.2023年的产量将是__________吨.
a(1–x)
年平均增长率为 x
50000
50 000(1 + x )
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
【提问】什么是下降额?下降率如何计算?
下降额=下降前的量-下降后的量
增长额=增长后的量-增长前的量
下降率= =
【提问】什么是增长额?增长率如何计算?
增长率= =
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
乙种药品成本的年平均下降额为(6000-3600)÷2=1200(元).
甲种药品成本的年平均下降额为(5000-3000)÷2=1000(元),
显然,乙种药品的年平均下降额较大,但是年平均下降额(元)不等同于年平均下降率(百分率)。
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
解:设甲种药品成本的年平均下降率为 x
一年后甲种药品成本为____________元,
两年后甲种药品成本为____________元.
列方程得=3000
解方程得 x1≈0.225,x2≈1.775(舍去).
答:甲种药品成本的年平均下降率为22.5%
-x)
【补充】下降率是用减少的数除以原数,则所得结果必定小于1,因此不能大于或等于1。
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
解:设乙种药品成本的年平均下降率为 y
一年后乙种药品成本为____________元,
两年后乙种药品成本为____________元.
列方程得=3600
解方程得 x1≈0.225,x2≈1.775(舍去).
答:乙种药品成本的年平均下降率为22.5%
1-y)
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
【问题】经过计算,你能得出什么结论?
【问题】成本下降额大的药品,它的成本下降率一定也大吗?
【问题】应怎样全面地比较几个对象的变化状况?
成本下降额表示绝对变化量,
成本下降率表示相对变化量,
两者兼顾才能全面比较对象的变化状况。
两种药品成本的年平均下降率相等
成本下降额较大的产品,其成本下降率不一定较大。
【详解】(1)设每个月生产成本的下降率为x,
根据题意得:400(1﹣x)2=361,
解得:x1=0.05=5%,x2=1.95(不合题意,舍去).
答:每个月生产成本的下降率为5%;
(2)361×(1﹣5%)=342.95(万元),
答:预测4月份该公司的生产成本为342.95万元.
例3 某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司2、3、4月每个月生产成本的下降率都相同.
(1)求每个月生产成本的下降率;
(2)请你预测4月份该公司的生产成本.
【详解】(1)解:设这两个月参观人数的月平均增长率为,
由题意得:,
解得:,(不合题意,舍去),
答:这两个月参观人数的月平均增长率为.
(2)(万人),
答:六月份的参观人数为13.31万人.
1.2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.
(1)求这两个月参观人数的月平均增长率;
(2)按照这个增长率,预计6月份的参观人数是多少?
1.2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,共有多少支队伍参加比赛?( )
A.8 B.10 C.7 D.9
2.某县年人均可支配收入为万元,年达到万元,若年至年间每年人均可支配收入的增长率都为,则下面所列方程正确的是( )
A. B.
C. D.
【详解】设有x支队伍,根据题意,得,解方程,得x1=10,x2=-9(舍去),故选B.
【详解】解:设年至年间每年人均可支配收入的增长率都为,根据题意得,
,故选:B.
【详解】
第一个月新建了301个充电桩,该市新建智能充电桩个数的月平均增长率为.
第二个月新建了个充电桩,
第三个月新建了个充电桩,
第三个月新建了500个充电桩,于是有,
故答案为.
3.为了加快数字化城市建设,某市计划新建一批智能充电桩,第一个月新建了301个充电桩,第三个月新建了500个充电桩,设该市新建智能充电桩个数的月平均增长率为,根据题意,请列出方程________.
【详解】(1)解:设这两个月中该景区游客人数的月平均增长率为,
由题意,得:,解得:(负值已舍掉);
答:这两个月中该景区游客人数的月平均增长率为;
(2)设5月份后10天日均接待游客人数是y万人,
由题意,得:,解得:;
∴5月份后10天日均接待游客人数最多是1万人.
4.随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.
(1)求这两个月中该景区游客人数的月平均增长率;
(2)预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?
【详解】
解:(1)设亩产量的平均增长率为x,
根据题意得:, 解得:,(舍去),
答:亩产量的平均增长率为20%.
(2)第四阶段的亩产量为(公斤),
∵,∴他们的目标可以实现.
5.“杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.
1. 本节课学习,你有哪些收获?请你用自己的语言简述一元二次方程解应用题的步骤?
2. 你知道本节课研究“传播问题”的基本特征吗?解决此类问题的关键步骤是什么?
“传播问题”的基本特征:以相同的速度逐轮传播。
解决此类问题的关键步骤:明确每轮传播中的传染源个数,以及这一轮被传染的总数。
第二十一章 一元二次方程
第一单元
21.3 实际问题与一元二次方程
第二课时 几何问题和数字问题
1.根据实际问题中的数量关系,正确列出一元二次方程。
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识。
复习巩固
探究新知
典例分析
针对训练
归纳小结
探究新知
典例分析
归纳小结
直击中考
布置作业
针对训练
【提问】回顾列方程解决实际问题的基本步骤
1)审:分清已知未知,明确数量关系;
2)设:设未知数;
3)列:列方程;
4)解:解方程;
5)验:根据实际验结果;
6) 答:写出答案。
【提问】计算下列图形面积
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
【分析】封面的长宽之比是9∶7,中央的矩形的长宽之比也应是9∶7。
设中央的矩形的长和宽分别是 9a cm和 7a cm,由此得上、下边衬与左、右边衬的宽度之比是:
9a
7a
(27-9a): (21-7a)= 9(3-a):7(3-a)= 9:7
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
解法一:设上、下边衬的宽均为9y cm ,左、右边衬的宽均为7y cm,
由题意得 (27-18y)(21-14y)=27
整理,得:16y 2 - 48y + 9 = 0
解方程,得y=
则y1=舍去)
答:上、下边衬的宽度为1.8cm,左、右边衬的宽度为1.4cm
所以9y=1.8 cm,7y=1.4 cm
【提问】为什么舍去2.8?请说明原因?
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
解法二:设正中央的矩形长和宽分别为9x cm,7x cm
由题意得 927
解方程,得x=
则x1=舍去)
答:上、下边衬的宽度为1.8cm,左、右边衬的宽度为1.4cm
故上、下边衬的宽度为≈1.8 cm,
左、右边衬的宽度为≈1.4 cm
如图,在一块长为 92m ,宽为 60m 的矩形耕地上挖三条水渠,水渠的宽都相等,水渠
把耕地分成面积均为 885m2 的 6 个小矩形,水渠应挖多宽?
【分析】设水渠宽为 x m,将所有耕地的面积拼在一起,变成一个新的矩形,它的长为 ___________m, 宽___________m.
60
92
60-x
92-2x
(92 – 2x )
(60-x)
解:设水渠的宽应挖 x m .
( 92 - 2x)(60 - x )= 6×885
解得 x1=105(舍去),x2=1
答:水渠应挖1米宽
如图,在一块长为 92m ,宽为 60m 的矩形耕地上挖三条水渠,水渠的宽都相等,水渠
把耕地分成面积均为 885m2 的 6 个小矩形,水渠应挖多宽?
【分析】设水渠宽为 x m,水渠的总面积为______________________________________________
92x
+260x
-2x2
解:设水渠的宽应挖 x m .
92×60 - 92x - 2×60x+ 2x2 = 6×885
解得 x1=105(舍去),x2=1
答:水渠应挖1米宽
例1 等腰梯形的面积为160cm2,上底比高多4cm,下底比上底多16cm,求这个梯形的高。
解:设这个梯形的高为 x cm,则上底为(x+4)cm,下底为(x+20)cm.
根据题意得(x+4+x+20)=160
整理,得x2 +12x -160= 0
解得 x1=8 , x2=-20 ( 不合题意,舍去 )
答:这个梯形的高为8cm.
1.如图,准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路,四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为_____米.
【详解】
设小路的宽度为,由题意得,由,可得.
2. 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,若墙长为18m,另三边用竹篱笆围成,篱笆总长35m,围成长方形的养鸡场四周不能有空隙.
(1)要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由.
【详解】
解:1)设养鸡场的宽为xm,根据题意得:x(35﹣2x)=150,
解得:x1=10,x2=7.5,
当x1=10时,35﹣2x=15<18,
当x2=7.5时35﹣2x=20>18,(舍去),
则养鸡场的宽是10m,长为15m.
2. 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,若墙长为18m,另三边用竹篱笆围成,篱笆总长35m,围成长方形的养鸡场四周不能有空隙.
(1)要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由.
【详解】
2)设养鸡场的宽为xm,根据题意得:x(35﹣2x)=200,
整理得:2x2﹣35x+200=0,
△=(﹣35)2﹣4×2×200=1225﹣1600=﹣375<0,
因为方程没有实数根,所以围成养鸡场的面积不能达到200m2.
几何问题
与一元二次方程
几何图形
常见几何图形周长或面积是等量关系.
类 型
课本封面问题
小路宽度问题
常采用图形平移,聚零为整方便列方程.
通过列方程式,算出周瑜去世时的年龄。
将题干内容转换为数学语言:
周瑜三十岁当东吴都督,去世时的年龄是两位数,十位数字比个位数字小三,个位数字的平方等于他去世时的年龄。
【详解】解:设周瑜去世时的年龄的个位数字为,则十位数字为,依题意得:
,
解得,,
当时,,(不合题意,舍去),
当时,(符合题意),
答:周瑜去世时的年龄为岁.
一个两位数的个位数字与十位数字的和为9,并且个位数字与十位数字的平方和为45,求这个两位数.
【详解】设个位数字为,则十位数字为.
得,
∴这个两位数为36或63.
【详解】设一位数为,则两位数为.
则根据题意可得:,
整理得:.
分解得:,
解得:,.
答:这个两位数为16或49.
典例2 一个两位数是一个一位数的平方,把这个一位数放在这个两位数的左边所成的三位数,比把这个一位数放在这个两位数的右边所成的三位数大,求这个两位数.
【详解】设其中较小的奇数为,则较大的奇数为,
根据题意,得,
解得,
当时,;
当时,.
故答案为:,或.
1 两个连续奇数的积为,若设其中较小的奇数为,则可列方程为_________________,这两个数分别为_______________.
1.第十四届国际数学教育大会(ICME—14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745,八进制是以8作为进位基数的数字系统,有0~7共8个基本数字,八进制数3745换算成十进制数是,表示ICME—14的举办年份.
(1)八进制数3747换算成十进制数是______;
(2)小华设计了一个n进制数234,换算成十进制数是193,求n的值.
【详解】(1)
(2)由题意,得,
解得,(舍负)
2 阅读材料,回答下列问题:
反序数:有这样一对数,一个数的数字排列完全颠倒过来变成另一个数,简单的说,就是顺序相反的两个数,我们把这样的一对数称为“反序数”,比如:的反序数是,的反序数是.
用方程知识解决问题:若一个两位数,其十位上的数字比个位上的数字大3,这个两位数与其反序数之积为,求这个两位数.
【详解】解:设这个两位数的个位数字为x,则十位数字为,
根据题意得:,
∴,即,
∴,
∴
解得x=2或(舍去),
∴,
∴这个两位数为.
3 如图,某中学课外兴题小组准备围建一个矩形花园 ABCD,其中一边靠墙,另外三边用总长为60 m的篱笆围成,与墙平行的一边 BC上要预留2 m宽的入口(如图中MN所示,不用篱笆),已知墙长为 28 m.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成500平方米的矩形花园 若能求出 BC长;若不能,说明理由.
【详解】(1)设矩形花园BC的长为x米,则其宽为(60﹣x+2)米,
依题意列方程得:(60﹣x+2)x=300,
解这个方程得:x1=12,x2=50,
∵28<50,∴x2=50(不合题意,舍去),
∴x=12.
答:当矩形的长BC为12米时,矩形花园的面积为300平方米;
3 如图,某中学课外兴题小组准备围建一个矩形花园 ABCD,其中一边靠墙,另外三边用总长为60 m的篱笆围成,与墙平行的一边 BC上要预留2 m宽的入口(如图中MN所示,不用篱笆),已知墙长为 28 m.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成500平方米的矩形花园 若能求出 BC长;若不能,说明理由.
(2)设矩形花园BC的长为x米,则其宽为(60﹣x+2)米,依题意列方程得:(60﹣x+2)x=500,
△=622﹣4000=﹣156<0,
则该方程无解,即不能围成500平方米的矩形花园.
答:不能围成500平方米的矩形花园.
1.如图,在长为50m,宽为38m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为1260m2,道路的宽应为多少?
【详解】解:设道路的宽应为x米,
由题意得 (50-2x)×(38-2x)=1260
解得:x1=4,x2=40(不符合题意,舍去)
答:道路的宽应为4m.
【详解】解:设这个最小数为.
根据题意,得x(x+8)=65.
解得,(不符合题意,舍去).
答:这个最小数为5.
2.2021年7日1日建党100周年纪念日,在本月日历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为65,求这个最小数(请用方程知识解答).
1. 本节课学习,你有哪些收获?请你用自己的语言简述一元二次方程解应用题的步骤?
2. 你知道解决“几何问题” 、“数字问题” 的关键步骤是什么?
第二十一章 一元二次方程
第一单元
21.3 实际问题与一元二次方程
第三课时 销售问题、图表问题、动点问题
1.根据实际问题中的数量关系,正确列出一元二次方程。
2.通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识。
复习巩固
探究新知
典例分析
针对训练
探究新知
典例分析
针对训练
归纳小结
直击中考
布置作业
探究新知
典例分析
针对训练
【提问】回顾列方程解决实际问题的基本步骤
1)审:分清已知未知,明确数量关系;
2)设:设未知数;
3)列:列方程;
4)解:解方程;
5)验:根据实际验结果;
6) 答:写出答案。
九年级学生小明在暑假期间勤工俭学。
1)他每天在批发市场以每斤2.5元买进黄瓜,再到市场以每斤4元卖掉黄瓜,那么他每卖1斤黄瓜可以赚到 元;
2)如果他每天都能卖完50斤黄瓜,则他每天收入是 元。
3)他每天外面吃饭需花费20元,则他每天实际可以获得_____________元。
1.5
75
单件售价-单件进价=单件利润
单件利润×销量=总利润
50
总利润-支出=实际利润(或:销售总额-成本总额-支出=实际利润)
【提问】根据上述问题,你能售价、进价、利润、支出之间存在的关系吗
[补充]1)利润率=100% 2)商品售价=标价
3)商品售价=商品进价(1+利润率)
某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减小库存,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1200元,那么衬衫的单价降了多少元?
【分析】设衬衫单价应降x元,
单件利润 销量 总利润
降价前
降价后
40-x
20+2x
设衬衫单价应降x元
由题意得(40-x)(20+2x)=1200
解方程得x1=20,x2=10
【提问】站在商家角度你觉得如何降价合适?
40
20
800
1200
∵尽快减小库存∴ x=20
答:衬衫的单价降了20元
某商店进了一批服装,进货单价为50元,若按每件60元出售,则可销售800件;若每件再提价1元出售,则其销售量就减少20件。现在预算要获利润12000元且进货成本不超过24000元,应按每件多少元出售?
【分析】设应按每件 x 元出售
进价 售价 单件利润 销量 总利润
提价前 50 60 10 800 8000
提价后 50
x
x-50
800-20(x-60)
12000
设应按每件 x 元出售
由题意得(x-50)[ 800-20(x-60)]=12000
解方程得x1=70,x2=80
当x=70时,50 (800-20 10)=30000>24000 舍去
当x=80时,50 (800-20 20)=20000<24000
答:应按每件 80 元出售,进货数量400件
某商店进了一批服装,进货单价为50元,若按每件60元出售,则可销售800件;若每件再提价1元出售,则其销售量就减少20件。现在预算要获利润12000元且进货成本不超过24000元,应按每件多少元出售?
【提问】如果设提价x元,你能根据提示信息列出方程吗?
设提价x元
由题意得(10+x)(800-20x)=12000
解方程得x1=10,x2=20
当x=10时,50 (800-20 10)=30000>24000 舍去
当x=20时,50 (800-20 20)=20000<24000
当x=20时,60+x=60+20=80 元
答:应按每件 80 元出售,进货数量400件
例1 某工厂生产的某种产品按供需要求分为十个档次.若生产第一档次(最低档次)的产品,一天可生产76件,每件的利润为10元,每提高一个档次,每件的利润增加2元,每天的产量将减少4件.设该产品的档次(每天只生产一个档次的产品)为x,请解答下列问题.
1)用含x的代数式表示:一天生产的产品件数为_______件,每件产品的利润为________元;
档次 销售量(件) 单件利润(元)
1(最低) 76 10
2
3
4
... ... ...
10(最高)
x
12
72
14
68
16
64
28
40
10+2(x-1)
76-4(x-1)
解(1)一天生产的产品件数为[76-4(x-1)]=(80-4x)件,
每件产品的利润为[10+2(x-1)]=(8+2x)元,
例1 某工厂生产的某种产品按供需要求分为十个档次.若生产第一档次(最低档次)的产品,一天可生产76件,每件的利润为10元,每提高一个档次,每件的利润增加2元,每天的产量将减少4件.设产品的档次(每天只生产一个档次的产品)为x,请解答下列问题.
2)若该产品一天的总利润为1080元,求这天生产产品的档次x的值.
(2)当利润是1080元时,即:[10+2(x-1)][76-4(x-1)]=1080,
整理得:-8x2+128x+640=1080,
解得:x1=5,x2=11,
∵x=11>10,不符合题意,舍去。∴x=5,
答:当生产产品的质量档次是在第5档次时,一天的总利润为1080元。
【详解】解:设每副羽毛球拍降价x元,
由题意得:(40-x)(20+5x)=1700,
整理得:x2-36x+180=0,
解方程得:x1=6,x2=30,
因为 每副降价幅度不超过15元,
所以 x=6符合题意,故答案是:6.
1.李华在网上开了一家羽毛球拍专卖店,平均每天可销售副,每个盈利元,若每副降价元,则每天可多销售副.如果每天要盈利元,每副应降价______元(要求每个降价幅度不超过元)
【详解】解:1)设每千克核桃应降价x元
根据题意,得(60﹣x﹣40)(100+×20)=2240,
化简,得 x2﹣10x+24=0,
解得x1=4,x2=6.
答:每千克核桃应降价4元或6元.
2.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
1)每千克核桃应降价多少元?
2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
2)由1)可知每千克核桃可降价4元或6元.
∵要尽可能让利于顾客,
∴每千克核桃应降价6元
此时,售价为:60﹣6=54(元),
答:该店应按原售价的九折出售.
2.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
1)每千克核桃应降价多少元?
2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
某公司组织一批员工到龙湾风景区旅游,支付给旅行社28000元,你能确定参加这次旅游的人数吗?
解:设参加旅游人数共有x人,
∵800×30=24000<28000,∴参加人数x>30,
根据题意,得x× [800-10(x-30)]=28000.
整理,得
解得,x1=40,x2=70
当x=40时, [800-10(x-30)]=800-10 (40-30)=700>500
当x=70时, [800-10(x-30)]=800-10 (70-30)=400<500(不符合题意,舍去)
答:参加人数共有40人
【分析】设参加旅游人数共有x人,公司支付给旅行社28000元,说明__________,则人均收费__________________________元
x>30
[800-10(x-30)]
为了节约用水,某水厂规定:某单元居民如果一个月的用水量不超过吨,那么这个月该单元居民只交10元水费.如果超过吨,则这个月除了仍要交10元水费外,超过那部分按每吨元交费.
1)该单元居民8月份用水80吨,超过了“规定的吨”,则超过部分应交水费 元(用含x的式子表示).
2)下表是该单元居民9月、10月的用水情况和交费情况:
根据上表数据,求该x吨是多少?
月份 用水量(吨) 交费总数(元)
9月份 85 25
10月份 50 10
【详解】
解:(1)超过的用水量为(80-x)吨,所以,超过部分应交水费(80-x)元;
(2)根据表格提供的数据,可以知道,根据9月份用水情况可以列出方程:(85-x)=25
解得,x1=60,x2=25
因为,所以x=60
答:该水厂规定的x吨是60吨.
例2 某市出租车收费标准如下(规定:四舍五入,精确到元,N≤15)N是走步价,李先生乘坐出租车打出的电子收费单是:里程11公里,应收29.1元,你能依据以上信息,推算出起步价N的值吗
里程x(km) 0<x≤3 3<x≤6 x>6
单价y(元) N
【详解】
由题意,可列出方程
整理得N2—29.1N+191=0.
解方程得N1=10,N2=19.1(不合题意舍去)
答:起步价是10元.
某公司组织一批员工到该风景区旅游,支付给旅行社2800元.A公司参加这次旅游的员工有多少人?某风景区的旅游信息如下:
旅游人数 收费标准
不超过30人 人均收费80元
超过30人 每增加1人,人均收费降低1元,但人均收费不低于55元
设参加这次旅游的员工有x人,
∵30×80=2400<2800,∴x>30.
根据题意得:x[80-(x-30)]=2800,
解得:x1=40,x2=70.
当x=40时,80-(x-30)=70>55,
当x=70时,80-(x-30)=40<55,舍去.
答:A公司参加这次旅游的员工有40人.
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动.几秒钟后△DPQ的面积等于28cm2?
A
B
C
D
P
Q
【提示】设x s后△DPQ的面积等于28cm2,则AP、PB、BQ、QC的长度分别可用含x的代数式表示,从而Rt △DAP 、 Rt △PBQ、 Rt △QCD的面积也都可以用含x的代数式表示,于是可以列出方程。
x
6
12
12-2x
2x
6-x
设x s后△DPQ的面积等于28cm2,则S△APD =______________
S△PBQ =________________, S△DCQ =_________________
根据题意得,
+ +28=72
化简得,
解方程得, x1=2,x2=4
答:2s或4s后△DPQ的面积等于28cm2
例3 如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C出发,点P以3cm/s的速度向点B移动,一直到达B为止;点Q以2cm/s的速度向点D移动。经过多长时间P、Q两点之间的距离是10cm?
设经过x s时间P、Q两点之间的距离是10cm。
3x
2x
2x
16-5x
解方程得x1=1.6,x2=4.8
答:1.6s或4.8s后P、Q距离是10cm
3x
2x
2x
16-5x
E
x=2时,由运动可知AP=3×2=6 cm,CQ=2×2=4 cm,
∴四边形ABCD是矩形,
∴QE=AD=6,
∴PE=AB﹣BE﹣AP=16﹣6﹣4=6,
根据勾股定理得PQ=,
∴当x=2 s时,P,Q两点的距离为6 cm;
2x
如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C出发,点P以3cm/s的速度向点B移动,一直到达B为止;点Q以2cm/s的速度向点D移动。
1)当运动时间为2s时,P,Q两点的距离为多少?
2)当运动时间为4s时,P,Q两点的距离为多少?
P’
x=4时,由运动知AP′=3×4=12 cm,CQ′=2×4=8 cm,
∴四边形ABCD是矩形,
∴P′E=AD=6,
P′B=CE=AB-AP′=16-12=4
∴Q′E=Q′C﹣CE=8﹣4=4,
根据勾股定理得P′Q′=,
∴当x=4 s时,P,Q两点的距离为cm;
Q’
E
如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C出发,点P以3cm/s的速度向点B移动,一直到达B为止;点Q以2cm/s的速度向点D移动。
1)当运动时间为2s时,P,Q两点的距离为多少?
2)当运动时间为4s时,P,Q两点的距离为多少?
【详解】解:(1)设与销售单价之间的函数关系式为:y=kx+b,
将点(1,110)、(3,130)代入一次函数表达式得:
,解得:,故函数的表达式为:y=10x+100;
(2)由题意得:(10x+100)(55-x-35)=1760,
整理,得.
解得,(舍去).所以55-x=43.
答:这种消毒液每桶实际售价43元.
1.某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量(桶)与每桶降价(元)()之间满足一次函数关系,其图象如图所示:
(1)求与之间的函数关系式;
(2)在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?
【详解】(1)若降价3元,则平均每天销售数量为20+2×3=26件.
(2)设每件商品应降价x元时,该商店每天销售利润为1200元.
根据题意,得(40-x)(20+2x)=1200,
解得:x1=10,x2=20.
∵要求每件盈利不少于25元,∴x2=20应舍去,∴x=10.
答:每件商品应降价10元时,该商店每天销售利润为1200元.
2.某商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为________件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
【详解】解:设该水果每千克降价x(x>0)元,
则每千克的利润为:元,销售量为:千克,
根据
或,
要尽可能让顾客得到实惠,
即售价为(元)
答:该水果的销售价为每千克29元.
3.端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求该水果的销售价为每千克多少元?
1. 本节课学习,你有哪些收获?请你用自己的语言简述一元二次方程解应用题的步骤?
2. 你知道解决“销售问题” 、“图表问题” 、“动点问题” 的关键步骤是什么?
1.某演出团体准备在苏州文化艺术中心大剧院举办迎新演出,该剧院有1200个座位,如果票价定为每张100元,那么门票可以全部售出如果票价每增加1元,那么门票就减少2张,要使得门票收入为245000元,票价应该定为多少元?
2.某超市销售一种矿泉水,进价为每箱24元,现在的售价为每箱36元,每月可销售60箱。经市场调查发现:若这种矿泉水的售价每降价1元,则每月的销量将增加10箱.如果该超市想要每月销售这种矿泉水的利润为650元,那么每箱矿泉水需要降价多少元?
3.如图,已知AB⊥BC,AB=12 cm,BC=8 cm.动点M从点A沿AB方向以2 cm/s的速度向点B运动,同时动点N从点C沿CB方向以1 cm/s的速度也向点B运动,其中一点到达B点时另一点也随之停止.当△MNB的面积为24 cm2时,求它们运动的时间.
1.解:设应定为x元,
则由题意可得:
即解得:
答:定价定为350元.
2.设每箱降价元,则每月可销售(10 +60)箱,
依题意得:(36 x 24)(10x+60)=650,
解得: (舍去).
答:每箱矿泉水需要降价7元.
3.解:根据题意可知cm, cm,
∴cm, cm,
∵△MNB的面积为24cm2,
∴,
解得:t1=2,t2=12(不合题意,舍去)
∴运动的时间为2s.
同课章节目录
