2.2 基本不等式 课件(40张PPT) 高一数学人教A版2019必修第一册
文档属性
| 名称 | 2.2 基本不等式 课件(40张PPT) 高一数学人教A版2019必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 18:06:37 | ||
图片预览











文档简介
(共41张PPT)
Mathematics
第2讲 不等式初步
PART 1 常见不等式
●
●
学数学,认准小叶
倒数法则
1、如果a>b>0,那么
2、如果0>a>b,那么
结论:如果a>b,且ab>0,那么
母题逻辑
同类变式
精益求精
考法1 不等式的概念与性质
下列命题是真命题的是( )
A、0>a>b→a >b
B、a >b →a>b>0
C、a>b→
D、a>b→a >b
例 1
★★☆☆☆ 2022江苏徐州市检测
考法1 不等式的概念与性质
方法:
①判断命题的真假;
②利用不等式性质求参;
③实际应用
同类变式
精益求精
考法1 不等式的概念与性质
已知a,b,c∈R,且c≠0,则下列命题中是真命题的是( )
A、如果a>b,则
B、如果ac<bc,那么a<b
C、如果a>b,那么
D、如果c>a>b>0,那么
互动题
★★☆☆☆ 多选题
母题逻辑
考法1 不等式的概念与性质
方法:
①判断命题的真假;
②利用不等式性质求参;
③实际应用
母题逻辑
同类变式
精益求精
考法1 不等式的概念与性质
已知c>a>b>0,求证:
拓展1
★★★☆☆
考法1 不等式的概念与性质
方法:
①判断命题的真假;
②利用不等式性质求参;
③实际应用
母题逻辑
同类变式
精益求精
考法1 不等式的概念与性质
已知a>b>0,c<0,求证:
拓展2
★★★☆☆
考法1 不等式的概念与性质
方法:
①判断命题的真假;
②利用不等式性质求参;
③实际应用
●
●
学数学,认准小叶
十字相乘法
拆两边,除中间
分解因式
例1 x -2x-8 例2 2x -x-6
母题逻辑
同类变式
精益求精
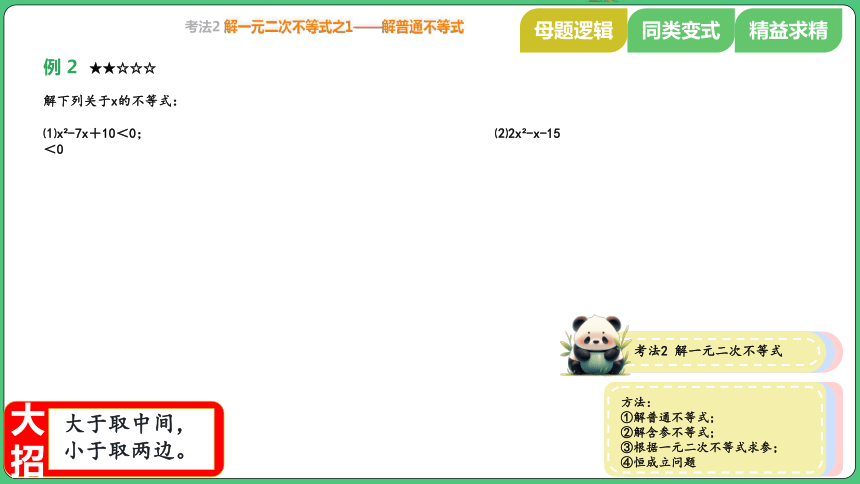
考法2 解一元二次不等式之1——解普通不等式
解下列关于x的不等式:
⑴x -7x+10<0; ⑵2x -x-15<0
例 2
★★☆☆☆
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
例 3
★★☆☆☆
解下列关于x的不等式:
⑴-2x -x+3≥0; ⑵-x +x+1≥0
考法2 解一元二次不等式之1——解普通不等式
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
考法2 解一元二次不等式之2——含参不等式恒成立
例 4
★★☆☆☆ 2022吉林吉林市月考
不等式x -kx+1>0对任意实数x都成立,则实数k的取值范围是____。
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2023陕西省汉中市期末
若关于x的不等式x +(k-1)x+4>0对一切实数恒成立,则实数k的取值范围是____。
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参
母题逻辑
同类变式
精益求精
例 5
★★☆☆☆ 2022西藏拉萨期末
若关于x的不等式x +ax+b>0的解集是{x∣x<-2或x>3},则a+b=( )
A、-7
B、-6
C、-5
D、1
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2023陕西省西安市期末
已知不等式ax -5x+b>0的解集是{x∣-3<x<-2},则a+b的值为( )
A、-7
B、7
C、
D、
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
例 6
★★☆☆☆ 2022辽宁锦州市期中
已知f(x)=(x-a)(x-2),解关于x的表达式f(x)<0.
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022广西钦州月考
求关于x的不等式x +(1-a)x-a<0的解集,其中a是常数。
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
考法3 解分式不等式
例 7
★★☆☆☆ 2022陕西咸阳市期中
不等式 的解集是( )
A、{x∣x<-1或x>3}
B、{x∣-1<x<3}
C、{x∣x<-3或x>1}
D、{x∣-3<x<1}
分式不等式:移项通分除化乘
考法3 解分式不等式
方法:移项通分除化乘
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022浙江温州月考
不等式 的解集是( )
A、{x∣ <x<1}
B、{x∣x<1}
C、{x∣x< 或x>1}
D、{x∣ <x<2}
考法3 解分式不等式
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022江苏常州月考
不等式 的解集是( )
A、{x∣ ≤x≤3}
B、{x∣ <x<3}
C、{x∣x≤ 或x>3}
D、{x∣x≥ }
考法3 解分式不等式
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
PART 2 基本不等式
●
●
学数学,认准小叶
基本不等式
如果a>0,b>0,那么 ,当且仅当a=b时,等号成立。
正
定
等
●
●
学数学,认准小叶
基本不等式推导——代数法
●
●
学数学,认准小叶
基本不等式推导——几何法
法1:赵爽弦图
●
●
学数学,认准小叶
基本不等式推导——几何法
法2:圆与半径
A
P
O
Q
B
C
学数学,认准小叶!
基本不等式必要点1
为什么a,b要为正数
完全平方差公式解释
学数学,认准小叶!
基本不等式必要点2
为什么有最值?
学数学,认准小叶!
基本不等式必要点2
为什么有最值?
一个x对应着唯一一个y
一个y可以对应着多个x
划
重
点
母题逻辑
同类变式
精益求精
考法4 基本不等式的直接应用
引例
★★☆☆☆ 北京西城区月考
已知正数x,y满足xy=16,则x+y( )
A、有最大值4 B、有最小值4 C、有最大值8 D、有最小值8
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
例8
★★☆☆☆
已知x>0,y>0,求:
⑴xy=12时,求3x+4y的最小值; ⑵2x+y=8时,xy的最大值。
考法4 基本不等式的直接应用
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022广东广州期中
已知x>0,y>0,且满足x+6y=6,则xy有( )
A、最大值
B、最小值
C、最大值1
D、最小值1
考法4 基本不等式的直接应用
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
精益求精
★★☆☆☆ 2023重庆期末
若正数a,b满足(a+1)(2b+1)=4,则a+2b+1的最小值为( )
A、2
B、3
C、
D、4
考法4 基本不等式的直接应用
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
考法5 基本不等式的必考模型之1——
例9
★★☆☆☆ 2022广东佛山市期中
若x>0,则 的最小值为____。
考法5 基本不等式必考模型
方法:
母题逻辑
同类变式
精益求精
考法5 基本不等式的必考模型之1——
互动题
★★☆☆☆ 2023江西上饶市模拟
的最小值为( )
A、 B、 C、 D、
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
精益求精
★★☆☆☆ 2022北京怀柔区期末
已知x>-1,则函数f(x)= 的最小值是____。
考法5 基本不等式的必考模型之1——
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
考法5 基本不等式的必考模型之1——
互动题
★★☆☆☆ 2020海南海口市月考
若x>1,则 的最小值等于( )
A、6 B、9 C、4 D、1
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
考法5 基本不等式的必考模型之2——换“1”模型
例10
★★☆☆☆ 2023吉林延边市期末
已知a>0,b>0,且 ,则4a+9b的最小值是( )
A、23
B、26
C、22
D、25
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022湖北模拟
已知正实数x,y满足x+y=2,则 的最小值为( )
A、 B、5 C、9 D、10
考法5 基本不等式的必考模型之2——换“1”模型
大招1:拖拽法
大招2:口诀——分子开根和平方,分母相加仍分母
母题逻辑
同类变式
精益求精
举一反三
★★☆☆☆ 黑龙江哈尔滨期末
已知a>0,b>0,且a+b=1,则 的最小值为____。
考法5 基本不等式的必考模型之2——换“1”模型
大招1:拖拽法
大招2:口诀——分子开根和平方,分母相加仍分母
母题逻辑
同类变式
精益求精
举一反三
★★☆☆☆ 2022四川模拟
已知ab为正实数,且 ,则a+b的最小值为____。
考法5 基本不等式的必考模型之2——换“1”模型
大招1:拖拽法
大招2:口诀——分子开根和平方,分母相加仍分母
母题逻辑
同类变式
精益求精
精益求精
★★☆☆☆ 2022四川模拟
若4m+n=1,其中mn>0,则 ____。
考法5 基本不等式的必考模型之2——换“1”模型
大招1:拖拽法
大招2:口诀——分子开根和平方,分母相加仍分母
母题逻辑
同类变式
精益求精
精益求精
★★☆☆☆ 2023湖南邵阳期中
若a>0,b>0,且(a-1)(b-1)=1,2a+8b的最小值为( )
A、12 B、14 C、16 D、18
考法5 基本不等式的必考模型之2——换“1”模型
口诀——分子开根和平方,分母相加仍分母
Mathematics
第2讲 不等式初步
PART 1 常见不等式
●
●
学数学,认准小叶
倒数法则
1、如果a>b>0,那么
2、如果0>a>b,那么
结论:如果a>b,且ab>0,那么
母题逻辑
同类变式
精益求精
考法1 不等式的概念与性质
下列命题是真命题的是( )
A、0>a>b→a >b
B、a >b →a>b>0
C、a>b→
D、a>b→a >b
例 1
★★☆☆☆ 2022江苏徐州市检测
考法1 不等式的概念与性质
方法:
①判断命题的真假;
②利用不等式性质求参;
③实际应用
同类变式
精益求精
考法1 不等式的概念与性质
已知a,b,c∈R,且c≠0,则下列命题中是真命题的是( )
A、如果a>b,则
B、如果ac<bc,那么a<b
C、如果a>b,那么
D、如果c>a>b>0,那么
互动题
★★☆☆☆ 多选题
母题逻辑
考法1 不等式的概念与性质
方法:
①判断命题的真假;
②利用不等式性质求参;
③实际应用
母题逻辑
同类变式
精益求精
考法1 不等式的概念与性质
已知c>a>b>0,求证:
拓展1
★★★☆☆
考法1 不等式的概念与性质
方法:
①判断命题的真假;
②利用不等式性质求参;
③实际应用
母题逻辑
同类变式
精益求精
考法1 不等式的概念与性质
已知a>b>0,c<0,求证:
拓展2
★★★☆☆
考法1 不等式的概念与性质
方法:
①判断命题的真假;
②利用不等式性质求参;
③实际应用
●
●
学数学,认准小叶
十字相乘法
拆两边,除中间
分解因式
例1 x -2x-8 例2 2x -x-6
母题逻辑
同类变式
精益求精
考法2 解一元二次不等式之1——解普通不等式
解下列关于x的不等式:
⑴x -7x+10<0; ⑵2x -x-15<0
例 2
★★☆☆☆
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
例 3
★★☆☆☆
解下列关于x的不等式:
⑴-2x -x+3≥0; ⑵-x +x+1≥0
考法2 解一元二次不等式之1——解普通不等式
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
考法2 解一元二次不等式之2——含参不等式恒成立
例 4
★★☆☆☆ 2022吉林吉林市月考
不等式x -kx+1>0对任意实数x都成立,则实数k的取值范围是____。
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2023陕西省汉中市期末
若关于x的不等式x +(k-1)x+4>0对一切实数恒成立,则实数k的取值范围是____。
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参
母题逻辑
同类变式
精益求精
例 5
★★☆☆☆ 2022西藏拉萨期末
若关于x的不等式x +ax+b>0的解集是{x∣x<-2或x>3},则a+b=( )
A、-7
B、-6
C、-5
D、1
大
招
大于取中间,
小于取两边。
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2023陕西省西安市期末
已知不等式ax -5x+b>0的解集是{x∣-3<x<-2},则a+b的值为( )
A、-7
B、7
C、
D、
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
例 6
★★☆☆☆ 2022辽宁锦州市期中
已知f(x)=(x-a)(x-2),解关于x的表达式f(x)<0.
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022广西钦州月考
求关于x的不等式x +(1-a)x-a<0的解集,其中a是常数。
考法2 解一元二次不等式之2——含参不等式恒成立
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
考法3 解分式不等式
例 7
★★☆☆☆ 2022陕西咸阳市期中
不等式 的解集是( )
A、{x∣x<-1或x>3}
B、{x∣-1<x<3}
C、{x∣x<-3或x>1}
D、{x∣-3<x<1}
分式不等式:移项通分除化乘
考法3 解分式不等式
方法:移项通分除化乘
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022浙江温州月考
不等式 的解集是( )
A、{x∣ <x<1}
B、{x∣x<1}
C、{x∣x< 或x>1}
D、{x∣ <x<2}
考法3 解分式不等式
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022江苏常州月考
不等式 的解集是( )
A、{x∣ ≤x≤3}
B、{x∣ <x<3}
C、{x∣x≤ 或x>3}
D、{x∣x≥ }
考法3 解分式不等式
考法2 解一元二次不等式
方法:
①解普通不等式;
②解含参不等式;
③根据一元二次不等式求参;
④恒成立问题
PART 2 基本不等式
●
●
学数学,认准小叶
基本不等式
如果a>0,b>0,那么 ,当且仅当a=b时,等号成立。
正
定
等
●
●
学数学,认准小叶
基本不等式推导——代数法
●
●
学数学,认准小叶
基本不等式推导——几何法
法1:赵爽弦图
●
●
学数学,认准小叶
基本不等式推导——几何法
法2:圆与半径
A
P
O
Q
B
C
学数学,认准小叶!
基本不等式必要点1
为什么a,b要为正数
完全平方差公式解释
学数学,认准小叶!
基本不等式必要点2
为什么有最值?
学数学,认准小叶!
基本不等式必要点2
为什么有最值?
一个x对应着唯一一个y
一个y可以对应着多个x
划
重
点
母题逻辑
同类变式
精益求精
考法4 基本不等式的直接应用
引例
★★☆☆☆ 北京西城区月考
已知正数x,y满足xy=16,则x+y( )
A、有最大值4 B、有最小值4 C、有最大值8 D、有最小值8
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
例8
★★☆☆☆
已知x>0,y>0,求:
⑴xy=12时,求3x+4y的最小值; ⑵2x+y=8时,xy的最大值。
考法4 基本不等式的直接应用
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022广东广州期中
已知x>0,y>0,且满足x+6y=6,则xy有( )
A、最大值
B、最小值
C、最大值1
D、最小值1
考法4 基本不等式的直接应用
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
精益求精
★★☆☆☆ 2023重庆期末
若正数a,b满足(a+1)(2b+1)=4,则a+2b+1的最小值为( )
A、2
B、3
C、
D、4
考法4 基本不等式的直接应用
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
考法5 基本不等式的必考模型之1——
例9
★★☆☆☆ 2022广东佛山市期中
若x>0,则 的最小值为____。
考法5 基本不等式必考模型
方法:
母题逻辑
同类变式
精益求精
考法5 基本不等式的必考模型之1——
互动题
★★☆☆☆ 2023江西上饶市模拟
的最小值为( )
A、 B、 C、 D、
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
精益求精
★★☆☆☆ 2022北京怀柔区期末
已知x>-1,则函数f(x)= 的最小值是____。
考法5 基本不等式的必考模型之1——
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
考法5 基本不等式的必考模型之1——
互动题
★★☆☆☆ 2020海南海口市月考
若x>1,则 的最小值等于( )
A、6 B、9 C、4 D、1
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
考法5 基本不等式的必考模型之2——换“1”模型
例10
★★☆☆☆ 2023吉林延边市期末
已知a>0,b>0,且 ,则4a+9b的最小值是( )
A、23
B、26
C、22
D、25
考法4 基本不等式的直接应用
方法:
①积定求和;
②和定求积
母题逻辑
同类变式
精益求精
互动题
★★☆☆☆ 2022湖北模拟
已知正实数x,y满足x+y=2,则 的最小值为( )
A、 B、5 C、9 D、10
考法5 基本不等式的必考模型之2——换“1”模型
大招1:拖拽法
大招2:口诀——分子开根和平方,分母相加仍分母
母题逻辑
同类变式
精益求精
举一反三
★★☆☆☆ 黑龙江哈尔滨期末
已知a>0,b>0,且a+b=1,则 的最小值为____。
考法5 基本不等式的必考模型之2——换“1”模型
大招1:拖拽法
大招2:口诀——分子开根和平方,分母相加仍分母
母题逻辑
同类变式
精益求精
举一反三
★★☆☆☆ 2022四川模拟
已知ab为正实数,且 ,则a+b的最小值为____。
考法5 基本不等式的必考模型之2——换“1”模型
大招1:拖拽法
大招2:口诀——分子开根和平方,分母相加仍分母
母题逻辑
同类变式
精益求精
精益求精
★★☆☆☆ 2022四川模拟
若4m+n=1,其中mn>0,则 ____。
考法5 基本不等式的必考模型之2——换“1”模型
大招1:拖拽法
大招2:口诀——分子开根和平方,分母相加仍分母
母题逻辑
同类变式
精益求精
精益求精
★★☆☆☆ 2023湖南邵阳期中
若a>0,b>0,且(a-1)(b-1)=1,2a+8b的最小值为( )
A、12 B、14 C、16 D、18
考法5 基本不等式的必考模型之2——换“1”模型
口诀——分子开根和平方,分母相加仍分母
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
