期末专题训练(二) 圆 同步练(含答案) 2025-2026学年数学苏科版(2024)九年级上册
文档属性
| 名称 | 期末专题训练(二) 圆 同步练(含答案) 2025-2026学年数学苏科版(2024)九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 445.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 22:18:05 | ||
图片预览


文档简介
期末专题训练(二) 圆
考点一 圆心角、弧、弦之间的关系定理与垂径定理
1 (2024镇江月考)如图,AB,CD是⊙O的弦,且AB=CD,若∠BOD=84°,则∠ACO的度数为( )
A. 42° B. 44° C. 46° D. 48°
(第1题) (第2题) (第3题) (第4题) (第5题)
2 (2024凉山州)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点A,B,连接AB,作AB的垂直平分线CD交AB于点D,交于点C,测出AB=40 cm,CD=10 cm,则圆形工件的半径为( )
A. 50 cm B. 35 cm C. 25 cm D. 20 cm
3 如图,AB是⊙O的弦,OC⊥AB,垂足为C,将劣弧AB沿弦AB折叠交于OC的中点D,若AB=2,则⊙O的半径为 .
4 如图,AB是⊙O的直径,弦CD交AB于点E,BE=1,AE=5,∠AEC=30°,则CD的长为 .
5 如图,在以点O为圆心的两个圆中,大圆的半径是小圆半径的2倍,大圆的弦AB和小圆交于C,D两点,若AC=CD=4,则小圆的半径是 .
考点二 圆周角定理及其推论
6 (2024海南)如图,AD是半圆O的直径,点B,C在半圆上,且==,点P在上,若∠PCB=130°,则∠PBA等于( )
A. 105° B. 100° C. 90° D. 70°
(第6题) (第8题) (第9题)
7 若圆O中弦AB等于半径R,则这条弦所对的圆周角度数为 .
8 (2024徐州新沂月考)如图,在圆内接四边形ABCD中,∠C=135°,AB⊥BD,以AB为y轴,BD为x轴,建立如图所示的平面直角坐标系,若点A的坐标为(0,3),则圆的直径为 .
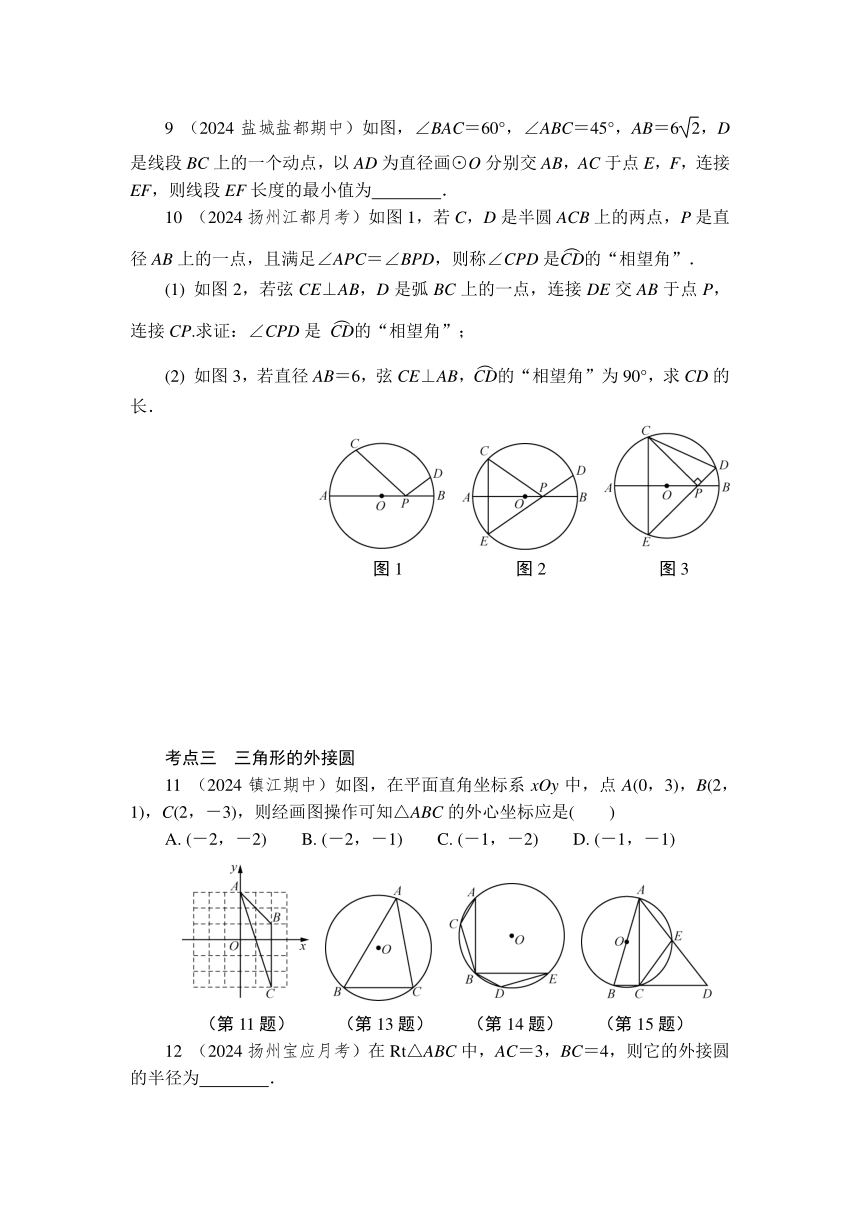
9 (2024盐城盐都期中)如图,∠BAC=60°,∠ABC=45°,AB=6,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于点E,F,连接EF,则线段EF长度的最小值为 .
10 (2024扬州江都月考)如图1,若C,D是半圆ACB上的两点,P是直径AB上的一点,且满足∠APC=∠BPD,则称∠CPD是的“相望角”.
(1) 如图2,若弦CE⊥AB,D是弧BC上的一点,连接DE交AB于点P,连接CP.求证:∠CPD是 的“相望角”;
(2) 如图3,若直径AB=6,弦CE⊥AB,的“相望角”为90°,求CD的长.
图1 图2 图3
考点三 三角形的外接圆
11 (2024镇江期中)如图,在平面直角坐标系xOy中,点A(0,3),B(2,1),C(2,-3),则经画图操作可知△ABC的外心坐标应是( )
A. (-2,-2) B. (-2,-1) C. (-1,-2) D. (-1,-1)
(第11题) (第13题) (第14题) (第15题)
12 (2024扬州宝应月考)在Rt△ABC中,AC=3,BC=4,则它的外接圆的半径为 .
13 (2024盐城东台月考)如图,⊙O是△ABC的外接圆,∠A=45°,BC=3,则⊙O的直径为 .
14 (2024南京月考)如图,△ABC是⊙O的内接三角形,∠A=30°,BC=,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C,D之间的距离为 .
15 (2024无锡宜兴期中)如图,在△ABC中,∠ACB=90°,BC=,△ABC的外接圆⊙O的半径为3,D是边BC的延长线上一点,连接AD,交⊙O于点E,连接CE.若△CED为等腰三角形,则线段BD的长度为 .
考点四 切线的性质及其判定
16 (2024福建)如图,点A,B在⊙O上,∠AOB=72°,直线MN与⊙O相切,切点为C,且C为 的中点,则∠ACM等于( )
A. 18° B. 30° C. 36° D. 72°
(第16题) (第17题) (第18题)
17 (2024常州溧阳期中)如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=24°,过点C作⊙O的切线交AB的延长线于点E,则∠E= .
18 (2024扬州邗江月考)如图,在Rt△ABC中,∠ACB=90°,AC=4,AB=5,D是AC上一点,E是BC上一点,DE=3,若以DE为直径的圆交AB于点M,N,则MN的最大值为 .
19 (2024镇江句容期中)如图,在△ABC中,AB=BC,AB为⊙O的直径,AC与⊙O相交于点D,过点D作DE⊥BC于点E,CB的延长线交⊙O于点F.
(1) 求证:DE为⊙O的切线;
(2) 若BE=1,BF=2,求AD的长.
考点五 三角形的内切圆
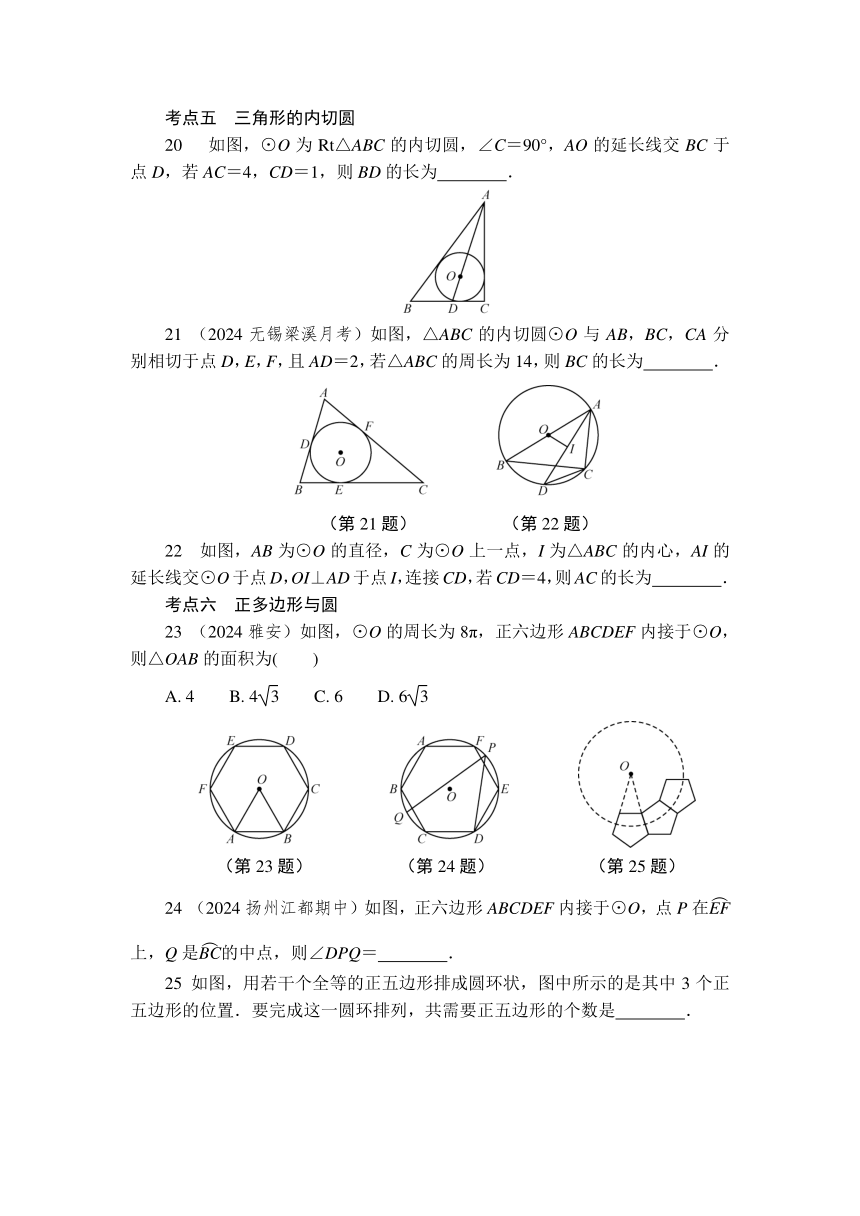
20 如图,⊙O为Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=4,CD=1,则BD的长为 .
21 (2024无锡梁溪月考)如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,若△ABC的周长为14,则BC的长为 .
(第21题) (第22题)
22 如图,AB为⊙O的直径,C为⊙O上一点,I为△ABC的内心,AI的延长线交⊙O于点D,OI⊥AD于点I,连接CD,若CD=4,则AC的长为 .
考点六 正多边形与圆
23 (2024雅安)如图,⊙O的周长为8π,正六边形ABCDEF内接于⊙O,则△OAB的面积为( )
A. 4 B. 4 C. 6 D. 6
(第23题) (第24题) (第25题)
24 (2024扬州江都期中)如图,正六边形ABCDEF内接于⊙O,点P在上,Q是的中点,则∠DPQ= .
25 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 .
考点七 弧长与扇形面积的计算
26 (2024青岛)如图,A,B,C,D是⊙O上的点,半径OA=3,=,∠DBC=25°,连接AD,则扇形AOB的面积为( )
A. B. C. D.
(第26题) (第27题) (第28题)
27 (2024吉林)某新建学校因场地限制,要合理规划体育场地.小明绘制的铅球场地设计图如图所示,该场地由⊙O和扇形OBC组成,OB,OC分别与⊙O交于点A,D. OA=1 m,OB=10 m,∠AOD=40°,则阴影部分的面积为
m2.(结果保留π)
28 (2024淮安盱眙期中)如图,AB为半圆O的直径,AB=12,BC为弦,若将沿弦BC翻折后恰好经过圆心O,则图中阴影部分的面积为 .
29 (2024无锡期中)如图,在△ABC中,AB=AC,以AB为直径的⊙O交边AC,BC于点D,H,连接BD,过点C作CE∥AB.连接AH,OC,AH与OC的交点G恰好落在BD上,若AB=40,则弦AD,AH和围成的图形的面积是 .
30 如图1,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E,F都在直线l上,且AB=7,EF=10,BC>5.点B以每秒1个单位长度的速度从点E处出发,沿射线EF的方向运动,矩形ABCD随之运动,运动时间为t s.如图2,当t=2.5 s时,求半圆O在矩形ABCD内的弧的长度.
图1 图2
考点八 圆锥的侧面积
31 (2024广州)如图,圆锥的侧面展开图是一个圆心角为72°的扇形,若扇形的半径l是5,则该圆锥的体积是( )
A. B. C. 2π D.
(第31题) (第33题) (第35题) (第36题)
32 (2024盐城)已知圆锥的底面半径为4,母线长为5,则该圆锥的侧面积为 .
33 (2024南京秦淮期中)如图,△ABC是一个圆锥的主视图,若AB=AC=5,BC=6,则该圆锥的侧面展开图的圆心角的度数为 .
34 沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若母线长l为6 cm,扇形的圆心角θ为120°,则圆锥的底面圆的半径r为 cm.
35 (2024苏州工业园区月考)如图,有一半径为1的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC,用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .
36 如图,在平行四边形ABCD中,AB=+1,BC=2,AH⊥CD,垂足为H,AH=.以点A为圆心,AH的长为半径画弧,与AB,AC,AD分别交于点E,F,G.若用扇形AEF围成一个圆锥的侧面,记这个圆锥底面圆的半径为r1;用扇形AHG围成另一个圆锥的侧面,记这个圆锥底面圆的半径为r2,则r1-r2= .
期末专题训练(二) 圆
1. D 2. C 3. 3 4. 4 5.
6. B 7. 30°或150° 8. 3 9. 3
10. (1) 证明:因为AB是直径,弦CE⊥AB,
所以AB垂直平分CE,
所以∠APC=∠APE.
因为∠APE=∠BPD,
所以∠APC=∠BPD,
所以∠CPD是的“相望角”.
(2) 解:由题意知,∠CPD是的“相望角”,∠CPD=90°,
所以∠CPE=90°,
因为直径AB=6,弦CE⊥AB,
所以∠PEC=∠PCE=45°.
如图,记圆心为O,连接OC,OD,则OC=OD=AB=3.
易得∠COD=2∠PEC=90°,
在Rt△COD中,由勾股定理,得CD==3,
所以CD的长为3.
11. B 12. 或2 13. 3 14. 2 15. 6或6或2
16. A 17. 42° 18.
19. (1) 证明:因为OA=OD,
所以∠A=∠ADO.
因为AB=BC,
所以∠A=∠C,
所以∠ADO=∠C,
所以OD∥BC.
因为DE⊥BC,
所以DE⊥OD.
因为OD是⊙O的半径,
所以DE是⊙O的切线.
(2) 解:如图,过点O作OH⊥CF于点H,则∠ODE=∠DEH=∠OHE=90°,
所以四边形ODEH是矩形,
所以OD=EH,OH=DE.
因为OF=OB,
所以BH=FH=1,
所以OD=EH=2,
所以AB=2OD=4,OH==,
所以DE=OH=,
所以BD==2,
所以AD===2.
20. 21. 5 22. 23. B 24. 45° 25. 10
26. A 27. 11π 28. 6π-9 29.
30. 解:设BC与半圆O交于点M.
当t=2.5 s时,BE=2.5.
因为EF=10,所以OE=EF=5,
所以OB=2.5,所以EB=OB.
在矩形ABCD中,∠ABC=90°,所以ME=MO.
又因为MO=EO,所以ME=EO=MO,
所以△MOE是等边三角形,所以∠EOM=60°,
所以的长为=,
所以半圆O在矩形ABCD内的弧的长度为.
31. D 32. 20π 33. 216° 34. 2 35. 36.
考点一 圆心角、弧、弦之间的关系定理与垂径定理
1 (2024镇江月考)如图,AB,CD是⊙O的弦,且AB=CD,若∠BOD=84°,则∠ACO的度数为( )
A. 42° B. 44° C. 46° D. 48°
(第1题) (第2题) (第3题) (第4题) (第5题)
2 (2024凉山州)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点A,B,连接AB,作AB的垂直平分线CD交AB于点D,交于点C,测出AB=40 cm,CD=10 cm,则圆形工件的半径为( )
A. 50 cm B. 35 cm C. 25 cm D. 20 cm
3 如图,AB是⊙O的弦,OC⊥AB,垂足为C,将劣弧AB沿弦AB折叠交于OC的中点D,若AB=2,则⊙O的半径为 .
4 如图,AB是⊙O的直径,弦CD交AB于点E,BE=1,AE=5,∠AEC=30°,则CD的长为 .
5 如图,在以点O为圆心的两个圆中,大圆的半径是小圆半径的2倍,大圆的弦AB和小圆交于C,D两点,若AC=CD=4,则小圆的半径是 .
考点二 圆周角定理及其推论
6 (2024海南)如图,AD是半圆O的直径,点B,C在半圆上,且==,点P在上,若∠PCB=130°,则∠PBA等于( )
A. 105° B. 100° C. 90° D. 70°
(第6题) (第8题) (第9题)
7 若圆O中弦AB等于半径R,则这条弦所对的圆周角度数为 .
8 (2024徐州新沂月考)如图,在圆内接四边形ABCD中,∠C=135°,AB⊥BD,以AB为y轴,BD为x轴,建立如图所示的平面直角坐标系,若点A的坐标为(0,3),则圆的直径为 .
9 (2024盐城盐都期中)如图,∠BAC=60°,∠ABC=45°,AB=6,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于点E,F,连接EF,则线段EF长度的最小值为 .
10 (2024扬州江都月考)如图1,若C,D是半圆ACB上的两点,P是直径AB上的一点,且满足∠APC=∠BPD,则称∠CPD是的“相望角”.
(1) 如图2,若弦CE⊥AB,D是弧BC上的一点,连接DE交AB于点P,连接CP.求证:∠CPD是 的“相望角”;
(2) 如图3,若直径AB=6,弦CE⊥AB,的“相望角”为90°,求CD的长.
图1 图2 图3
考点三 三角形的外接圆
11 (2024镇江期中)如图,在平面直角坐标系xOy中,点A(0,3),B(2,1),C(2,-3),则经画图操作可知△ABC的外心坐标应是( )
A. (-2,-2) B. (-2,-1) C. (-1,-2) D. (-1,-1)
(第11题) (第13题) (第14题) (第15题)
12 (2024扬州宝应月考)在Rt△ABC中,AC=3,BC=4,则它的外接圆的半径为 .
13 (2024盐城东台月考)如图,⊙O是△ABC的外接圆,∠A=45°,BC=3,则⊙O的直径为 .
14 (2024南京月考)如图,△ABC是⊙O的内接三角形,∠A=30°,BC=,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C,D之间的距离为 .
15 (2024无锡宜兴期中)如图,在△ABC中,∠ACB=90°,BC=,△ABC的外接圆⊙O的半径为3,D是边BC的延长线上一点,连接AD,交⊙O于点E,连接CE.若△CED为等腰三角形,则线段BD的长度为 .
考点四 切线的性质及其判定
16 (2024福建)如图,点A,B在⊙O上,∠AOB=72°,直线MN与⊙O相切,切点为C,且C为 的中点,则∠ACM等于( )
A. 18° B. 30° C. 36° D. 72°
(第16题) (第17题) (第18题)
17 (2024常州溧阳期中)如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=24°,过点C作⊙O的切线交AB的延长线于点E,则∠E= .
18 (2024扬州邗江月考)如图,在Rt△ABC中,∠ACB=90°,AC=4,AB=5,D是AC上一点,E是BC上一点,DE=3,若以DE为直径的圆交AB于点M,N,则MN的最大值为 .
19 (2024镇江句容期中)如图,在△ABC中,AB=BC,AB为⊙O的直径,AC与⊙O相交于点D,过点D作DE⊥BC于点E,CB的延长线交⊙O于点F.
(1) 求证:DE为⊙O的切线;
(2) 若BE=1,BF=2,求AD的长.
考点五 三角形的内切圆
20 如图,⊙O为Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=4,CD=1,则BD的长为 .
21 (2024无锡梁溪月考)如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,若△ABC的周长为14,则BC的长为 .
(第21题) (第22题)
22 如图,AB为⊙O的直径,C为⊙O上一点,I为△ABC的内心,AI的延长线交⊙O于点D,OI⊥AD于点I,连接CD,若CD=4,则AC的长为 .
考点六 正多边形与圆
23 (2024雅安)如图,⊙O的周长为8π,正六边形ABCDEF内接于⊙O,则△OAB的面积为( )
A. 4 B. 4 C. 6 D. 6
(第23题) (第24题) (第25题)
24 (2024扬州江都期中)如图,正六边形ABCDEF内接于⊙O,点P在上,Q是的中点,则∠DPQ= .
25 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 .
考点七 弧长与扇形面积的计算
26 (2024青岛)如图,A,B,C,D是⊙O上的点,半径OA=3,=,∠DBC=25°,连接AD,则扇形AOB的面积为( )
A. B. C. D.
(第26题) (第27题) (第28题)
27 (2024吉林)某新建学校因场地限制,要合理规划体育场地.小明绘制的铅球场地设计图如图所示,该场地由⊙O和扇形OBC组成,OB,OC分别与⊙O交于点A,D. OA=1 m,OB=10 m,∠AOD=40°,则阴影部分的面积为
m2.(结果保留π)
28 (2024淮安盱眙期中)如图,AB为半圆O的直径,AB=12,BC为弦,若将沿弦BC翻折后恰好经过圆心O,则图中阴影部分的面积为 .
29 (2024无锡期中)如图,在△ABC中,AB=AC,以AB为直径的⊙O交边AC,BC于点D,H,连接BD,过点C作CE∥AB.连接AH,OC,AH与OC的交点G恰好落在BD上,若AB=40,则弦AD,AH和围成的图形的面积是 .
30 如图1,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E,F都在直线l上,且AB=7,EF=10,BC>5.点B以每秒1个单位长度的速度从点E处出发,沿射线EF的方向运动,矩形ABCD随之运动,运动时间为t s.如图2,当t=2.5 s时,求半圆O在矩形ABCD内的弧的长度.
图1 图2
考点八 圆锥的侧面积
31 (2024广州)如图,圆锥的侧面展开图是一个圆心角为72°的扇形,若扇形的半径l是5,则该圆锥的体积是( )
A. B. C. 2π D.
(第31题) (第33题) (第35题) (第36题)
32 (2024盐城)已知圆锥的底面半径为4,母线长为5,则该圆锥的侧面积为 .
33 (2024南京秦淮期中)如图,△ABC是一个圆锥的主视图,若AB=AC=5,BC=6,则该圆锥的侧面展开图的圆心角的度数为 .
34 沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若母线长l为6 cm,扇形的圆心角θ为120°,则圆锥的底面圆的半径r为 cm.
35 (2024苏州工业园区月考)如图,有一半径为1的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC,用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .
36 如图,在平行四边形ABCD中,AB=+1,BC=2,AH⊥CD,垂足为H,AH=.以点A为圆心,AH的长为半径画弧,与AB,AC,AD分别交于点E,F,G.若用扇形AEF围成一个圆锥的侧面,记这个圆锥底面圆的半径为r1;用扇形AHG围成另一个圆锥的侧面,记这个圆锥底面圆的半径为r2,则r1-r2= .
期末专题训练(二) 圆
1. D 2. C 3. 3 4. 4 5.
6. B 7. 30°或150° 8. 3 9. 3
10. (1) 证明:因为AB是直径,弦CE⊥AB,
所以AB垂直平分CE,
所以∠APC=∠APE.
因为∠APE=∠BPD,
所以∠APC=∠BPD,
所以∠CPD是的“相望角”.
(2) 解:由题意知,∠CPD是的“相望角”,∠CPD=90°,
所以∠CPE=90°,
因为直径AB=6,弦CE⊥AB,
所以∠PEC=∠PCE=45°.
如图,记圆心为O,连接OC,OD,则OC=OD=AB=3.
易得∠COD=2∠PEC=90°,
在Rt△COD中,由勾股定理,得CD==3,
所以CD的长为3.
11. B 12. 或2 13. 3 14. 2 15. 6或6或2
16. A 17. 42° 18.
19. (1) 证明:因为OA=OD,
所以∠A=∠ADO.
因为AB=BC,
所以∠A=∠C,
所以∠ADO=∠C,
所以OD∥BC.
因为DE⊥BC,
所以DE⊥OD.
因为OD是⊙O的半径,
所以DE是⊙O的切线.
(2) 解:如图,过点O作OH⊥CF于点H,则∠ODE=∠DEH=∠OHE=90°,
所以四边形ODEH是矩形,
所以OD=EH,OH=DE.
因为OF=OB,
所以BH=FH=1,
所以OD=EH=2,
所以AB=2OD=4,OH==,
所以DE=OH=,
所以BD==2,
所以AD===2.
20. 21. 5 22. 23. B 24. 45° 25. 10
26. A 27. 11π 28. 6π-9 29.
30. 解:设BC与半圆O交于点M.
当t=2.5 s时,BE=2.5.
因为EF=10,所以OE=EF=5,
所以OB=2.5,所以EB=OB.
在矩形ABCD中,∠ABC=90°,所以ME=MO.
又因为MO=EO,所以ME=EO=MO,
所以△MOE是等边三角形,所以∠EOM=60°,
所以的长为=,
所以半圆O在矩形ABCD内的弧的长度为.
31. D 32. 20π 33. 216° 34. 2 35. 36.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
