期末综合测试卷 同步练 (含答案) 2025-2026学年数学苏科版(2024)九年级上册
文档属性
| 名称 | 期末综合测试卷 同步练 (含答案) 2025-2026学年数学苏科版(2024)九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 324.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 23:03:14 | ||
图片预览



文档简介
期末综合测试卷
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. 用配方法解方程x2+4x-1=0,变形正确的是( )
A. (x+2)2=5 B. (x+4)2=5
C. (x+2)2=1 D. (x+4)2=1
2. (2024连云港海州月考)一组数据3,2,4,2,5的中位数和众数分别是( )
A. 3,2 B. 3,3 C. 4,2 D. 4,3
3. 若关于x的一元二次方程x2-3x+m=0有两个相等的实数根,则实数m的值为( )
A. -9 B. - C. D. 9
4. 如图,已知点A,B,C在⊙O上,C为的中点.若∠BAC=35°,则∠AOB等于( )
A. 140° B. 120° C. 110° D. 70°
(第4题) (第6题) (第7题) (第8题)
5. (2024盐城大丰月考)某机械厂一月份生产零件50万个,三月份生产零件72万个,则该机械厂二、三月份生产零件数量的月平均增长率为( )
A. 2% B. 5% C. 10% D. 20%
6. 如图,O为正六边形ABCDEF对角线FD上一点,假设可以随机在正六边形中取点,那么这个点取在阴影部分的概率是( )
A. B. C. D.
7. 如图,I为△ABC的内心,有一直线通过点I且分别与AB,AC相交于点D,E.若AD=DE=5,AE=6,则点I到BC的距离为( )
A. B. C. 2 D. 3
8. (2024南通海门月考)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A. 0 B. 1 C. 2 D. 3
二、 填空题(每小题3分,共24分)
9. 一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n=________.
10. 学校举行科技创新比赛,各项成绩均按百分制计,再按照创新设计占60%,现场展示占40%计算选手的综合成绩(百分制).小华本次比赛的各项成绩分别是:创新设计85分,现场展示90分,则他的综合成绩是________分.
11. 用圆心角为120°,半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是________.
12. 如图,边长为的正方形ABCD内接于⊙O,分别过点A,D作⊙O的切线,两条切线交于点P,则图中阴影部分的面积是________.
(第12题) (第14题) (第16题)
13. (2024南通崇川月考)若关于x的方程x2+(a-1)x+a2=0的两根互为倒数,则a=________.
14. 如图,△ABC内接于⊙O且∠ACB=90°,弦CD平分∠ACB,连接AD,BD.若AB=5,AC=4,则BD=________,CD=________.
15. 定义新运算:对于两个不相等的实数a,b,我们规定符号max{a,b}表示a,b中的较大值,如:max{2,4}=4,max{-2,-4}=-2.按照这个规定,若max{x,-x}=,则x的值是________.
16. (2024盐城盐都月考)如图,在矩形ABCD中,AB=3,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为________.
三、 解答题(共102分)
17. (12分)用适当方法解下列方程:
(1) 4(x-5)2=16; (2) 3x2+2x-3=0;
(1) 3(x-1)2=x(x-1); (4) 3x2-6x-2=0.
18. (8分)(2024常州)在3张相同的小纸条上分别写有“石头”“剪子”“布”.将这3张小纸条做成3支签,放在不透明的盒子中搅匀.
(1) 从盒子中任意抽出1支签,抽到“石头”的概率是________;
(2) 甲、乙两人通过抽签分胜负,规定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”.甲先从盒子中任意抽出1支签(不放回),乙再从余下的2支签中任意抽出1支签,求甲取胜的概率.
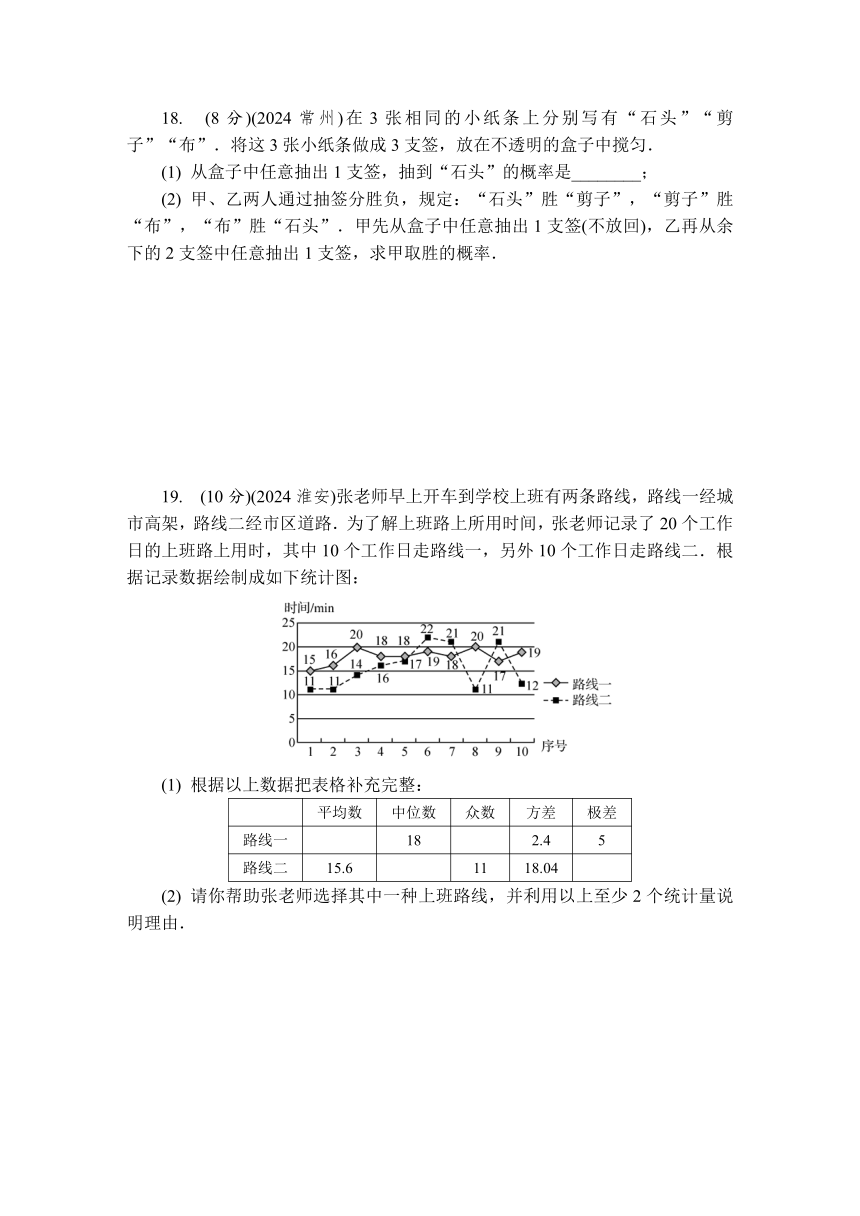
19. (10分)(2024淮安)张老师早上开车到学校上班有两条路线,路线一经城市高架,路线二经市区道路.为了解上班路上所用时间,张老师记录了20个工作日的上班路上用时,其中10个工作日走路线一,另外10个工作日走路线二.根据记录数据绘制成如下统计图:
(1) 根据以上数据把表格补充完整:
平均数 中位数 众数 方差 极差
路线一 18 2.4 5
路线二 15.6 11 18.04
(2) 请你帮助张老师选择其中一种上班路线,并利用以上至少2个统计量说明理由.
20. (10分)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的⊙O与AC相交于点D,E为上的一点,且∠ADE=40°.
(1) 求的长;
(2) 若∠EAD=76°,求证:CB为⊙O的切线.
21. (8分)已知关于x的一元二次方程x2-(2m-1)x-3m2+m=0.
(1) 求证:无论m为何值,方程总有实数根;
(2) 若x1,x2是方程的两个实数根,且+=-,求m的值.
22. (10分)某宾馆共有房间40间,当每间房间定价为300元/天时,可全部住满. 每间房间定价每增加10元/天,未入住的房间将增加1间. 入住的房间的维护费为20元/天,未入住的房间的维护费为5元/天.
(1) 当每间房间定价为360元/天时,入住的房间有________间;
(2) 若该宾馆每天的收入要达到11 350元,每间房间定价为多少元/天?(宾馆每天的收入=入住的房费-维护费)
23. (10分)如图,AB是⊙O的直径,过点A作⊙O的切线AC,P是射线AC上的动点,连接OP,过点B作BD∥OP,交⊙O于点D,连接PD.
(1) 求证:PD是⊙O的切线;
(2) 当四边形POBD是平行四边形时,求∠APO的度数.
备用图
24. (10分)(2024常州天宁期中)如图,AB是⊙O的直径,点C在⊙O上,请用无刻度直尺画图(保留作图痕迹,不写画法).
(1) 如图1,若M是半圆的中点,且与点C在同一侧,画出∠ACB的平分线CN.并说明理由;
(2) 如图2,若DE∥AB,画出∠ACB的平分线CP;
(3) 在(2)的作图下,已知AC=4,BC=3,CP交直径AB于点F,则AF= .
图1 图2
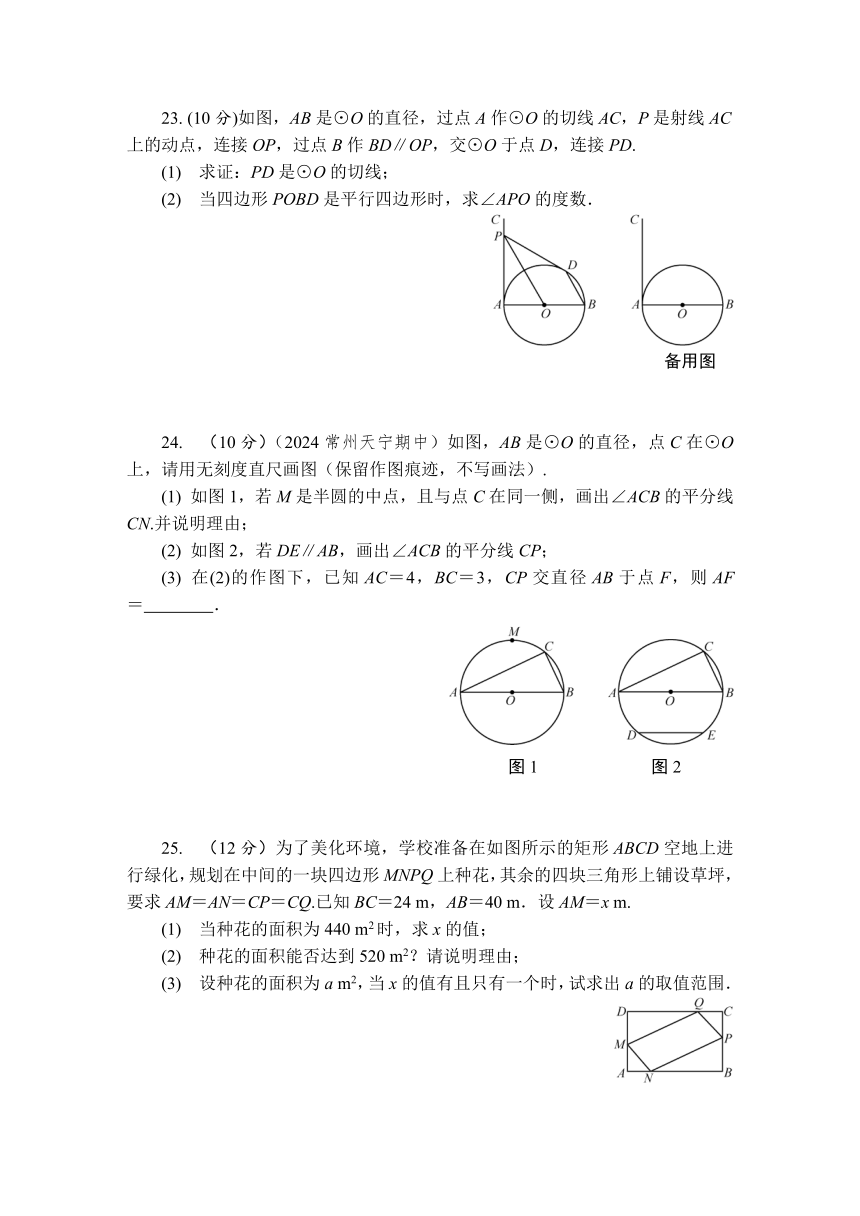
25. (12分)为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNPQ上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24 m,AB=40 m.设AM=x m.
(1) 当种花的面积为440 m2时,求x的值;
(2) 种花的面积能否达到520 m2?请说明理由;
(3) 设种花的面积为a m2,当x的值有且只有一个时,试求出a的取值范围.
26. (12分)(2024盐城盐都期中)
【发现结论】
一元二次方程的几何解法最早可以追溯到古希腊,小聪同学在了解到英格兰著名文学家卡莱尔给出的几何解法后,也有了他自己的新发现:如图1,在平面直角坐标系中,已知点A(0,a),B(-b,c),以AB为直径作⊙M.若⊙M与x轴交于点P(s,0),Q(t,0),则s,t为关于x的方程x2+bx+ac=0的两个实数根.
【探究思考】
(1) 由题意,得∠APB=90°,AP2=s2+a2,BP2=(-b-s)2+c2,AB2=b2+(a-c)2.
在Rt△ABP中,由AP2+BP2=AB2,得s2+a2+(-b-s)2+c2=b2+(a-c)2,
化简,得 ,同理可得 .
所以s,t为方程x2+bx+ac=0的两个实数根.
【灵活运用】
(2) 如图2,x1,x2为方程 的两个实数根.
(3) 在图3中所给网格图的x轴上画出以方程x2-3x-2=0两根为横坐标的点P,Q.
(4) 已知点A(0,-8),B(8,-2),以AB为直径作⊙C.根据小聪的发现判断⊙C与x轴的位置关系,并说明理由.
图1 图2 图3
期末综合测试卷
1. A 2. A 3. C 4. A 5. D 6. B 7. A 8. B
9. 9 10. 87 11. 4 12. 1- 13. -1
14. 15. -1或 16. 6-3
17. (1) x1=7,x2=3
(2) x1=,x2=
(3) x1=1,x2=
(4) x1=1+,x2=1-
18. 解:(1)
(2) 列表如下:
甲 乙
石头 剪子 布
石头 (石头,剪子) (石头,布)
剪子 (剪子,石头) (剪子,布)
布 (布,石头) (布,剪子)
共有6种等可能的结果,其中甲取胜的结果有:(石头,剪子),(剪子,布),(布,石头),共3种,
所以甲取胜的概率为=.
19. 解:(1) 路线一:18,18;
路线二:15,11.
(2) 路线二的平均数小于路线一,路线二的中位数小于路线一,路线二的众数小于路线一,则选路线二.(答案不唯一,合理即可)
20. (1) 解:如图,连接OE.
因为∠ADE=40°,
所以∠AOE=2∠ADE=80°,
所以∠EOB=180°-∠AOE=100°.
因为AB=4,所以⊙O半径长是2,
所以的长==.
(2) 证明:因为∠EAB=∠EOB=50°,
所以∠BAC=∠EAD-∠EAB=76°-50°=26°.
因为∠C=64°,所以∠C+∠BAC=90°,
所以∠ABC=180°-(∠C+∠BAC)=90°,
所以AB⊥BC,又AB为⊙O的直径,
所以CB为⊙O的切线.
21. (1) 证明:因为Δ=[-(2m-1)]2-4×1×(-3m2+m)=4m2-4m+1+12m2-4m=16m2-8m+1=(4m-1)2≥0,
所以方程总有实数根.
(2) 解:由题意知,x1+x2=2m-1,x1x2=-3m2+m.
因为+==-2=-,
所以-2=-,
整理,得5m2-7m+2=0,解得m=1或m=.
22. 解:(1) 34
(2) 设每间房间定价为x元/天.
根据题意,得x(40-)-20×(40-)-5×=11 350,
整理,得x2-715x+126 000=0,
解得x1=315,x2=400.
当x=315时,未入住房间为1.5间,不符合题意,
故每间房间定价为400元/天.
23. (1) 证明:如图1,连接OD.
因为PA切⊙O于点A,
所以PA⊥AB,即∠PAO=90°.
因为BD∥OP,
所以∠DBO=∠AOP,∠BDO=∠DOP.
因为OD=OB,所以∠BDO=∠DBO,
所以∠DOP=∠AOP.
在△AOP和△DOP中,
所以△AOP≌△DOP(SAS),所以∠PDO=∠PAO.
因为∠PAO=90°,所以∠PDO=90°,即OD⊥PD.
因为OD为⊙O的半径,所以PD是⊙O的切线.
(2) 解:由(1),得△AOP≌△DOP,则PA=PD.
如图2,因为四边形POBD是平行四边形,所以PD=OB.
因为OB=OA,所以PA=OA,所以∠APO=∠AOP.
因为∠PAO=90°,所以∠APO=∠AOP=45°.
图1 图2
24. 解:(1) 如图1,射线CN即为所求.理由如下:
因为=,MN是直径,
所以=,
所以∠ACN=∠BCN,
即CN平分∠ACB.
(2) 如图2,射线CP即为所求.
(3) 解析:如图2,过点F作FM⊥BC于点M,FN⊥AC于点N.因为AB是⊙O的直径,所以∠ACB=90°,所以AB===5.因为CF平分∠ACB,FM⊥BC,FN⊥AC,所以FM=FN.因为===,所以AF=AB=.
图1 图2
25. 解:(1) 根据题意,得24×40-2×(40-x)(24-x)-2×x2=440,
整理,得x2-32x+220=0,即(x-22)(x-10)=0,
解得x1=22,x2=10,
则x的值为22或10.
(2) 种花的面积不能达到520 m2,理由如下:
根据题意,得24×40-2×(40-x)(24-x)-2×x2=520,
整理,得x2-32x+260=0.
因为b2-4ac=322-4×260=1 024-1 040=-16<0,
所以此方程无解,故种花面积不能达到520 m2.
(3) 根据题意,得24×40-2×(40-x)(24-x)-2×x2=a,
整理,得x2-32x+=0.
①当方程有两个相等根时,满足x的值有且只有一个,
所以Δ=322-4×=0,
即2a=1 024,解得a=512;
②当方程有两个不等根时,0<x<24,a为面积,
所以Δ=322-4×>0,解得0<a<512,
解得x1=16+,x2=16-,
所以x1≥24,
所以≥8,解得0<a≤384.
综上,a=512或0<a≤384.
26. 解:(1) s2+bs+ac=0 t2+bt+ac=0
(2) x2-5x+3=0
(3) 由题意,得-b=3,ac=-2,
取a=1,则c=-2,
即点A(0,1),B(3,-2),
以AB为对角线作正方形ATBS,正方形对角线的交点为圆心R,
以AR为半径作圆R,交x轴于点P,Q即为所求点.
(4) ⊙C与x轴的位置关系为相切,理由如下:
由点A,B的坐标知,a=-8,b=-8,c=-2,
则对应的方程为x2-8x+16=0,
解得x=4,
即方程有两个相等的解,
故⊙C与x轴的位置关系为相切.
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. 用配方法解方程x2+4x-1=0,变形正确的是( )
A. (x+2)2=5 B. (x+4)2=5
C. (x+2)2=1 D. (x+4)2=1
2. (2024连云港海州月考)一组数据3,2,4,2,5的中位数和众数分别是( )
A. 3,2 B. 3,3 C. 4,2 D. 4,3
3. 若关于x的一元二次方程x2-3x+m=0有两个相等的实数根,则实数m的值为( )
A. -9 B. - C. D. 9
4. 如图,已知点A,B,C在⊙O上,C为的中点.若∠BAC=35°,则∠AOB等于( )
A. 140° B. 120° C. 110° D. 70°
(第4题) (第6题) (第7题) (第8题)
5. (2024盐城大丰月考)某机械厂一月份生产零件50万个,三月份生产零件72万个,则该机械厂二、三月份生产零件数量的月平均增长率为( )
A. 2% B. 5% C. 10% D. 20%
6. 如图,O为正六边形ABCDEF对角线FD上一点,假设可以随机在正六边形中取点,那么这个点取在阴影部分的概率是( )
A. B. C. D.
7. 如图,I为△ABC的内心,有一直线通过点I且分别与AB,AC相交于点D,E.若AD=DE=5,AE=6,则点I到BC的距离为( )
A. B. C. 2 D. 3
8. (2024南通海门月考)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A. 0 B. 1 C. 2 D. 3
二、 填空题(每小题3分,共24分)
9. 一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n=________.
10. 学校举行科技创新比赛,各项成绩均按百分制计,再按照创新设计占60%,现场展示占40%计算选手的综合成绩(百分制).小华本次比赛的各项成绩分别是:创新设计85分,现场展示90分,则他的综合成绩是________分.
11. 用圆心角为120°,半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是________.
12. 如图,边长为的正方形ABCD内接于⊙O,分别过点A,D作⊙O的切线,两条切线交于点P,则图中阴影部分的面积是________.
(第12题) (第14题) (第16题)
13. (2024南通崇川月考)若关于x的方程x2+(a-1)x+a2=0的两根互为倒数,则a=________.
14. 如图,△ABC内接于⊙O且∠ACB=90°,弦CD平分∠ACB,连接AD,BD.若AB=5,AC=4,则BD=________,CD=________.
15. 定义新运算:对于两个不相等的实数a,b,我们规定符号max{a,b}表示a,b中的较大值,如:max{2,4}=4,max{-2,-4}=-2.按照这个规定,若max{x,-x}=,则x的值是________.
16. (2024盐城盐都月考)如图,在矩形ABCD中,AB=3,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为________.
三、 解答题(共102分)
17. (12分)用适当方法解下列方程:
(1) 4(x-5)2=16; (2) 3x2+2x-3=0;
(1) 3(x-1)2=x(x-1); (4) 3x2-6x-2=0.
18. (8分)(2024常州)在3张相同的小纸条上分别写有“石头”“剪子”“布”.将这3张小纸条做成3支签,放在不透明的盒子中搅匀.
(1) 从盒子中任意抽出1支签,抽到“石头”的概率是________;
(2) 甲、乙两人通过抽签分胜负,规定:“石头”胜“剪子”,“剪子”胜“布”,“布”胜“石头”.甲先从盒子中任意抽出1支签(不放回),乙再从余下的2支签中任意抽出1支签,求甲取胜的概率.
19. (10分)(2024淮安)张老师早上开车到学校上班有两条路线,路线一经城市高架,路线二经市区道路.为了解上班路上所用时间,张老师记录了20个工作日的上班路上用时,其中10个工作日走路线一,另外10个工作日走路线二.根据记录数据绘制成如下统计图:
(1) 根据以上数据把表格补充完整:
平均数 中位数 众数 方差 极差
路线一 18 2.4 5
路线二 15.6 11 18.04
(2) 请你帮助张老师选择其中一种上班路线,并利用以上至少2个统计量说明理由.
20. (10分)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的⊙O与AC相交于点D,E为上的一点,且∠ADE=40°.
(1) 求的长;
(2) 若∠EAD=76°,求证:CB为⊙O的切线.
21. (8分)已知关于x的一元二次方程x2-(2m-1)x-3m2+m=0.
(1) 求证:无论m为何值,方程总有实数根;
(2) 若x1,x2是方程的两个实数根,且+=-,求m的值.
22. (10分)某宾馆共有房间40间,当每间房间定价为300元/天时,可全部住满. 每间房间定价每增加10元/天,未入住的房间将增加1间. 入住的房间的维护费为20元/天,未入住的房间的维护费为5元/天.
(1) 当每间房间定价为360元/天时,入住的房间有________间;
(2) 若该宾馆每天的收入要达到11 350元,每间房间定价为多少元/天?(宾馆每天的收入=入住的房费-维护费)
23. (10分)如图,AB是⊙O的直径,过点A作⊙O的切线AC,P是射线AC上的动点,连接OP,过点B作BD∥OP,交⊙O于点D,连接PD.
(1) 求证:PD是⊙O的切线;
(2) 当四边形POBD是平行四边形时,求∠APO的度数.
备用图
24. (10分)(2024常州天宁期中)如图,AB是⊙O的直径,点C在⊙O上,请用无刻度直尺画图(保留作图痕迹,不写画法).
(1) 如图1,若M是半圆的中点,且与点C在同一侧,画出∠ACB的平分线CN.并说明理由;
(2) 如图2,若DE∥AB,画出∠ACB的平分线CP;
(3) 在(2)的作图下,已知AC=4,BC=3,CP交直径AB于点F,则AF= .
图1 图2
25. (12分)为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNPQ上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24 m,AB=40 m.设AM=x m.
(1) 当种花的面积为440 m2时,求x的值;
(2) 种花的面积能否达到520 m2?请说明理由;
(3) 设种花的面积为a m2,当x的值有且只有一个时,试求出a的取值范围.
26. (12分)(2024盐城盐都期中)
【发现结论】
一元二次方程的几何解法最早可以追溯到古希腊,小聪同学在了解到英格兰著名文学家卡莱尔给出的几何解法后,也有了他自己的新发现:如图1,在平面直角坐标系中,已知点A(0,a),B(-b,c),以AB为直径作⊙M.若⊙M与x轴交于点P(s,0),Q(t,0),则s,t为关于x的方程x2+bx+ac=0的两个实数根.
【探究思考】
(1) 由题意,得∠APB=90°,AP2=s2+a2,BP2=(-b-s)2+c2,AB2=b2+(a-c)2.
在Rt△ABP中,由AP2+BP2=AB2,得s2+a2+(-b-s)2+c2=b2+(a-c)2,
化简,得 ,同理可得 .
所以s,t为方程x2+bx+ac=0的两个实数根.
【灵活运用】
(2) 如图2,x1,x2为方程 的两个实数根.
(3) 在图3中所给网格图的x轴上画出以方程x2-3x-2=0两根为横坐标的点P,Q.
(4) 已知点A(0,-8),B(8,-2),以AB为直径作⊙C.根据小聪的发现判断⊙C与x轴的位置关系,并说明理由.
图1 图2 图3
期末综合测试卷
1. A 2. A 3. C 4. A 5. D 6. B 7. A 8. B
9. 9 10. 87 11. 4 12. 1- 13. -1
14. 15. -1或 16. 6-3
17. (1) x1=7,x2=3
(2) x1=,x2=
(3) x1=1,x2=
(4) x1=1+,x2=1-
18. 解:(1)
(2) 列表如下:
甲 乙
石头 剪子 布
石头 (石头,剪子) (石头,布)
剪子 (剪子,石头) (剪子,布)
布 (布,石头) (布,剪子)
共有6种等可能的结果,其中甲取胜的结果有:(石头,剪子),(剪子,布),(布,石头),共3种,
所以甲取胜的概率为=.
19. 解:(1) 路线一:18,18;
路线二:15,11.
(2) 路线二的平均数小于路线一,路线二的中位数小于路线一,路线二的众数小于路线一,则选路线二.(答案不唯一,合理即可)
20. (1) 解:如图,连接OE.
因为∠ADE=40°,
所以∠AOE=2∠ADE=80°,
所以∠EOB=180°-∠AOE=100°.
因为AB=4,所以⊙O半径长是2,
所以的长==.
(2) 证明:因为∠EAB=∠EOB=50°,
所以∠BAC=∠EAD-∠EAB=76°-50°=26°.
因为∠C=64°,所以∠C+∠BAC=90°,
所以∠ABC=180°-(∠C+∠BAC)=90°,
所以AB⊥BC,又AB为⊙O的直径,
所以CB为⊙O的切线.
21. (1) 证明:因为Δ=[-(2m-1)]2-4×1×(-3m2+m)=4m2-4m+1+12m2-4m=16m2-8m+1=(4m-1)2≥0,
所以方程总有实数根.
(2) 解:由题意知,x1+x2=2m-1,x1x2=-3m2+m.
因为+==-2=-,
所以-2=-,
整理,得5m2-7m+2=0,解得m=1或m=.
22. 解:(1) 34
(2) 设每间房间定价为x元/天.
根据题意,得x(40-)-20×(40-)-5×=11 350,
整理,得x2-715x+126 000=0,
解得x1=315,x2=400.
当x=315时,未入住房间为1.5间,不符合题意,
故每间房间定价为400元/天.
23. (1) 证明:如图1,连接OD.
因为PA切⊙O于点A,
所以PA⊥AB,即∠PAO=90°.
因为BD∥OP,
所以∠DBO=∠AOP,∠BDO=∠DOP.
因为OD=OB,所以∠BDO=∠DBO,
所以∠DOP=∠AOP.
在△AOP和△DOP中,
所以△AOP≌△DOP(SAS),所以∠PDO=∠PAO.
因为∠PAO=90°,所以∠PDO=90°,即OD⊥PD.
因为OD为⊙O的半径,所以PD是⊙O的切线.
(2) 解:由(1),得△AOP≌△DOP,则PA=PD.
如图2,因为四边形POBD是平行四边形,所以PD=OB.
因为OB=OA,所以PA=OA,所以∠APO=∠AOP.
因为∠PAO=90°,所以∠APO=∠AOP=45°.
图1 图2
24. 解:(1) 如图1,射线CN即为所求.理由如下:
因为=,MN是直径,
所以=,
所以∠ACN=∠BCN,
即CN平分∠ACB.
(2) 如图2,射线CP即为所求.
(3) 解析:如图2,过点F作FM⊥BC于点M,FN⊥AC于点N.因为AB是⊙O的直径,所以∠ACB=90°,所以AB===5.因为CF平分∠ACB,FM⊥BC,FN⊥AC,所以FM=FN.因为===,所以AF=AB=.
图1 图2
25. 解:(1) 根据题意,得24×40-2×(40-x)(24-x)-2×x2=440,
整理,得x2-32x+220=0,即(x-22)(x-10)=0,
解得x1=22,x2=10,
则x的值为22或10.
(2) 种花的面积不能达到520 m2,理由如下:
根据题意,得24×40-2×(40-x)(24-x)-2×x2=520,
整理,得x2-32x+260=0.
因为b2-4ac=322-4×260=1 024-1 040=-16<0,
所以此方程无解,故种花面积不能达到520 m2.
(3) 根据题意,得24×40-2×(40-x)(24-x)-2×x2=a,
整理,得x2-32x+=0.
①当方程有两个相等根时,满足x的值有且只有一个,
所以Δ=322-4×=0,
即2a=1 024,解得a=512;
②当方程有两个不等根时,0<x<24,a为面积,
所以Δ=322-4×>0,解得0<a<512,
解得x1=16+,x2=16-,
所以x1≥24,
所以≥8,解得0<a≤384.
综上,a=512或0<a≤384.
26. 解:(1) s2+bs+ac=0 t2+bt+ac=0
(2) x2-5x+3=0
(3) 由题意,得-b=3,ac=-2,
取a=1,则c=-2,
即点A(0,1),B(3,-2),
以AB为对角线作正方形ATBS,正方形对角线的交点为圆心R,
以AR为半径作圆R,交x轴于点P,Q即为所求点.
(4) ⊙C与x轴的位置关系为相切,理由如下:
由点A,B的坐标知,a=-8,b=-8,c=-2,
则对应的方程为x2-8x+16=0,
解得x=4,
即方程有两个相等的解,
故⊙C与x轴的位置关系为相切.
同课章节目录
