微专题3求不规则图形的阴影面积 同步练 (含答案) 2025-2026学年数学苏科版(2024)九年级上册
文档属性
| 名称 | 微专题3求不规则图形的阴影面积 同步练 (含答案) 2025-2026学年数学苏科版(2024)九年级上册 | 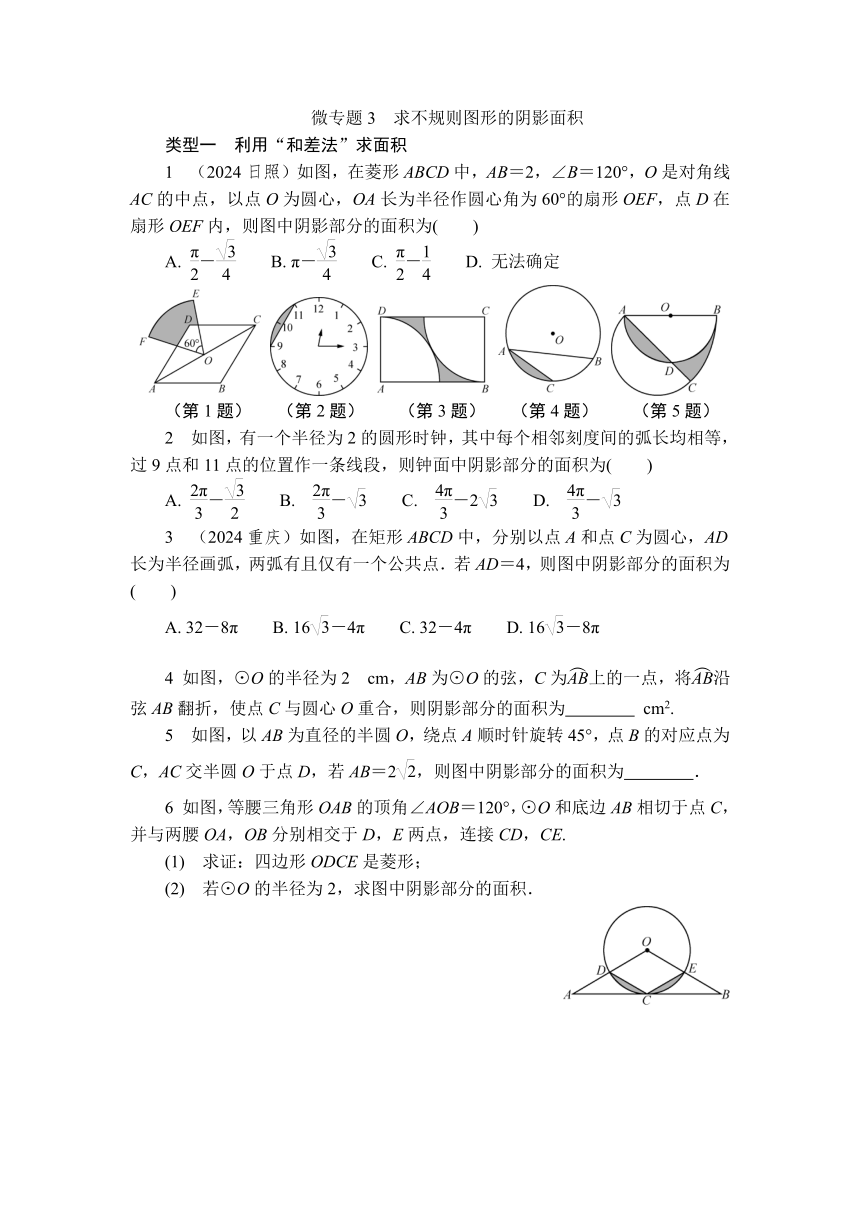 | |
| 格式 | docx | ||
| 文件大小 | 174.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 23:04:20 | ||
图片预览



文档简介
微专题3 求不规则图形的阴影面积
类型一 利用“和差法”求面积
1 (2024日照)如图,在菱形ABCD中,AB=2,∠B=120°,O是对角线AC的中点,以点O为圆心,OA长为半径作圆心角为60°的扇形OEF,点D在扇形OEF内,则图中阴影部分的面积为( )
A. - B. π- C. - D. 无法确定
(第1题) (第2题) (第3题) (第4题) (第5题)
2 如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A. - B. - C. -2 D. -
3 (2024重庆)如图,在矩形ABCD中,分别以点A和点C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A. 32-8π B. 16-4π C. 32-4π D. 16-8π
4 如图,⊙O的半径为2 cm,AB为⊙O的弦,C为上的一点,将沿弦AB翻折,使点C与圆心O重合,则阴影部分的面积为 cm2.
5 如图,以AB为直径的半圆O,绕点A顺时针旋转45°,点B的对应点为C,AC交半圆O于点D,若AB=2,则图中阴影部分的面积为 .
6 如图,等腰三角形OAB的顶角∠AOB=120°,⊙O和底边AB相切于点C,并与两腰OA,OB分别相交于D,E两点,连接CD,CE.
(1) 求证:四边形ODCE是菱形;
(2) 若⊙O的半径为2,求图中阴影部分的面积.
类型二 利用“割补法”求面积
7 如图,某玩具品牌的标志由半径为1 cm的三个等圆构成,且三个等圆⊙O1,⊙O2,⊙O3相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A. cm2 B. cm2 C. cm2 D. π cm2
(第7题) (第8题) (第9题) (第10题)
8 (2024泰安)两个半径相等的半圆按如图方式放置,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A. - B. C. - D. -
9 (2024宿迁沭阳期中)如图,将半径OB=6的半圆绕点B按顺时针方向旋转30°,此时点A到了点A′,则图中阴影部分的面积为 .(结果保留π)
10 如图,正方形ABCD的边长为2,O为对角线的交点,E,F分别为BC,AD的中点.以点C为圆心,2为半径作,再分别以点E,F为圆心,1为半径作,,则图中阴影部分的面积为 .(结果保留π)
类型三 利用“等积法”求面积
11 如图,半圆的直径AB=40,C,D是半圆上的三等分点,E是OA的中点,则阴影部分的面积为 .(结果保留π)
(第11题) (第12题) (第13题) (第14题)
12 如图是两个半圆,点O为大半圆的圆心,AB是大半圆的弦且与小半圆相切,且AB=24,则图中阴影部分的面积为 .(结果保留π)
13 (2024扬州邗江期中)如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若∠BED=45°,AB=2,则阴影部分的面积为 .(结果保留π)
14 如图,AB为⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=8,CD=5,图中阴影部分的面积为8π,则EF= .
微专题3 求不规则图形的阴影面积
类型一 利用“和差法”求面积
1 (2024日照)如图,在菱形ABCD中,AB=2,∠B=120°,O是对角线AC的中点,以点O为圆心,OA长为半径作圆心角为60°的扇形OEF,点D在扇形OEF内,则图中阴影部分的面积为( )
A. - B. π- C. - D. 无法确定
(第1题) (第2题) (第3题) (第4题) (第5题)
2 如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A. - B. - C. -2 D. -
3 (2024重庆)如图,在矩形ABCD中,分别以点A和点C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A. 32-8π B. 16-4π C. 32-4π D. 16-8π
4 如图,⊙O的半径为2 cm,AB为⊙O的弦,C为上的一点,将沿弦AB翻折,使点C与圆心O重合,则阴影部分的面积为 cm2.
5 如图,以AB为直径的半圆O,绕点A顺时针旋转45°,点B的对应点为C,AC交半圆O于点D,若AB=2,则图中阴影部分的面积为 .
6 如图,等腰三角形OAB的顶角∠AOB=120°,⊙O和底边AB相切于点C,并与两腰OA,OB分别相交于D,E两点,连接CD,CE.
(1) 求证:四边形ODCE是菱形;
(2) 若⊙O的半径为2,求图中阴影部分的面积.
类型二 利用“割补法”求面积
7 如图,某玩具品牌的标志由半径为1 cm的三个等圆构成,且三个等圆⊙O1,⊙O2,⊙O3相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A. cm2 B. cm2 C. cm2 D. π cm2
(第7题) (第8题) (第9题) (第10题)
8 (2024泰安)两个半径相等的半圆按如图方式放置,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A. - B. C. - D. -
9 (2024宿迁沭阳期中)如图,将半径OB=6的半圆绕点B按顺时针方向旋转30°,此时点A到了点A′,则图中阴影部分的面积为 .(结果保留π)
10 如图,正方形ABCD的边长为2,O为对角线的交点,E,F分别为BC,AD的中点.以点C为圆心,2为半径作,再分别以点E,F为圆心,1为半径作,,则图中阴影部分的面积为 .(结果保留π)
类型三 利用“等积法”求面积
11 如图,半圆的直径AB=40,C,D是半圆上的三等分点,E是OA的中点,则阴影部分的面积为 .(结果保留π)
(第11题) (第12题) (第13题) (第14题)
12 如图是两个半圆,点O为大半圆的圆心,AB是大半圆的弦且与小半圆相切,且AB=24,则图中阴影部分的面积为 .(结果保留π)
13 (2024扬州邗江期中)如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若∠BED=45°,AB=2,则阴影部分的面积为 .(结果保留π)
14 如图,AB为⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=8,CD=5,图中阴影部分的面积为8π,则EF= .
微专题3 求不规则图形的阴影面积
1. A 2. B 3. D 4. - 5. π-2
6. (1) 证明:连接OC.
因为⊙O和底边AB相切于点C,所以OC⊥AB.
因为OA=OB,∠AOB=120°,
所以∠AOC=∠BOC=∠AOB=60°.
因为OD=OC,OC=OE,
所以△ODC和△OCE都是等边三角形,
所以OD=OC=DC,OC=OE=CE,
所以OD=CD=CE=OE,
所以四边形ODCE是菱形.
(2) 解:连接DE交OC于点F.
因为四边形ODCE是菱形,
所以OF=OC=1,DE=2DF,∠OFD=90°.
在Rt△ODF中,OD=2,
所以DF===,
所以DE=2DF=2,
所以图中阴影部分的面积=扇形ODE的面积-菱形ODCE的面积=-OC·DE=-×2×2=-2,
所以图中阴影部分的面积为-2.
7. C 8. A 9. 12π 10. π-2 11. 12. 72π
13. 14.
类型一 利用“和差法”求面积
1 (2024日照)如图,在菱形ABCD中,AB=2,∠B=120°,O是对角线AC的中点,以点O为圆心,OA长为半径作圆心角为60°的扇形OEF,点D在扇形OEF内,则图中阴影部分的面积为( )
A. - B. π- C. - D. 无法确定
(第1题) (第2题) (第3题) (第4题) (第5题)
2 如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A. - B. - C. -2 D. -
3 (2024重庆)如图,在矩形ABCD中,分别以点A和点C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A. 32-8π B. 16-4π C. 32-4π D. 16-8π
4 如图,⊙O的半径为2 cm,AB为⊙O的弦,C为上的一点,将沿弦AB翻折,使点C与圆心O重合,则阴影部分的面积为 cm2.
5 如图,以AB为直径的半圆O,绕点A顺时针旋转45°,点B的对应点为C,AC交半圆O于点D,若AB=2,则图中阴影部分的面积为 .
6 如图,等腰三角形OAB的顶角∠AOB=120°,⊙O和底边AB相切于点C,并与两腰OA,OB分别相交于D,E两点,连接CD,CE.
(1) 求证:四边形ODCE是菱形;
(2) 若⊙O的半径为2,求图中阴影部分的面积.
类型二 利用“割补法”求面积
7 如图,某玩具品牌的标志由半径为1 cm的三个等圆构成,且三个等圆⊙O1,⊙O2,⊙O3相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A. cm2 B. cm2 C. cm2 D. π cm2
(第7题) (第8题) (第9题) (第10题)
8 (2024泰安)两个半径相等的半圆按如图方式放置,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A. - B. C. - D. -
9 (2024宿迁沭阳期中)如图,将半径OB=6的半圆绕点B按顺时针方向旋转30°,此时点A到了点A′,则图中阴影部分的面积为 .(结果保留π)
10 如图,正方形ABCD的边长为2,O为对角线的交点,E,F分别为BC,AD的中点.以点C为圆心,2为半径作,再分别以点E,F为圆心,1为半径作,,则图中阴影部分的面积为 .(结果保留π)
类型三 利用“等积法”求面积
11 如图,半圆的直径AB=40,C,D是半圆上的三等分点,E是OA的中点,则阴影部分的面积为 .(结果保留π)
(第11题) (第12题) (第13题) (第14题)
12 如图是两个半圆,点O为大半圆的圆心,AB是大半圆的弦且与小半圆相切,且AB=24,则图中阴影部分的面积为 .(结果保留π)
13 (2024扬州邗江期中)如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若∠BED=45°,AB=2,则阴影部分的面积为 .(结果保留π)
14 如图,AB为⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=8,CD=5,图中阴影部分的面积为8π,则EF= .
微专题3 求不规则图形的阴影面积
类型一 利用“和差法”求面积
1 (2024日照)如图,在菱形ABCD中,AB=2,∠B=120°,O是对角线AC的中点,以点O为圆心,OA长为半径作圆心角为60°的扇形OEF,点D在扇形OEF内,则图中阴影部分的面积为( )
A. - B. π- C. - D. 无法确定
(第1题) (第2题) (第3题) (第4题) (第5题)
2 如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A. - B. - C. -2 D. -
3 (2024重庆)如图,在矩形ABCD中,分别以点A和点C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A. 32-8π B. 16-4π C. 32-4π D. 16-8π
4 如图,⊙O的半径为2 cm,AB为⊙O的弦,C为上的一点,将沿弦AB翻折,使点C与圆心O重合,则阴影部分的面积为 cm2.
5 如图,以AB为直径的半圆O,绕点A顺时针旋转45°,点B的对应点为C,AC交半圆O于点D,若AB=2,则图中阴影部分的面积为 .
6 如图,等腰三角形OAB的顶角∠AOB=120°,⊙O和底边AB相切于点C,并与两腰OA,OB分别相交于D,E两点,连接CD,CE.
(1) 求证:四边形ODCE是菱形;
(2) 若⊙O的半径为2,求图中阴影部分的面积.
类型二 利用“割补法”求面积
7 如图,某玩具品牌的标志由半径为1 cm的三个等圆构成,且三个等圆⊙O1,⊙O2,⊙O3相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A. cm2 B. cm2 C. cm2 D. π cm2
(第7题) (第8题) (第9题) (第10题)
8 (2024泰安)两个半径相等的半圆按如图方式放置,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A. - B. C. - D. -
9 (2024宿迁沭阳期中)如图,将半径OB=6的半圆绕点B按顺时针方向旋转30°,此时点A到了点A′,则图中阴影部分的面积为 .(结果保留π)
10 如图,正方形ABCD的边长为2,O为对角线的交点,E,F分别为BC,AD的中点.以点C为圆心,2为半径作,再分别以点E,F为圆心,1为半径作,,则图中阴影部分的面积为 .(结果保留π)
类型三 利用“等积法”求面积
11 如图,半圆的直径AB=40,C,D是半圆上的三等分点,E是OA的中点,则阴影部分的面积为 .(结果保留π)
(第11题) (第12题) (第13题) (第14题)
12 如图是两个半圆,点O为大半圆的圆心,AB是大半圆的弦且与小半圆相切,且AB=24,则图中阴影部分的面积为 .(结果保留π)
13 (2024扬州邗江期中)如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若∠BED=45°,AB=2,则阴影部分的面积为 .(结果保留π)
14 如图,AB为⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=8,CD=5,图中阴影部分的面积为8π,则EF= .
微专题3 求不规则图形的阴影面积
1. A 2. B 3. D 4. - 5. π-2
6. (1) 证明:连接OC.
因为⊙O和底边AB相切于点C,所以OC⊥AB.
因为OA=OB,∠AOB=120°,
所以∠AOC=∠BOC=∠AOB=60°.
因为OD=OC,OC=OE,
所以△ODC和△OCE都是等边三角形,
所以OD=OC=DC,OC=OE=CE,
所以OD=CD=CE=OE,
所以四边形ODCE是菱形.
(2) 解:连接DE交OC于点F.
因为四边形ODCE是菱形,
所以OF=OC=1,DE=2DF,∠OFD=90°.
在Rt△ODF中,OD=2,
所以DF===,
所以DE=2DF=2,
所以图中阴影部分的面积=扇形ODE的面积-菱形ODCE的面积=-OC·DE=-×2×2=-2,
所以图中阴影部分的面积为-2.
7. C 8. A 9. 12π 10. π-2 11. 12. 72π
13. 14.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
