1.4 用一元二次方程解决问题 同步练(含答案) 2025-2026学年数学苏科版(2024)九年级上册
文档属性
| 名称 | 1.4 用一元二次方程解决问题 同步练(含答案) 2025-2026学年数学苏科版(2024)九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 281.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 00:00:00 | ||
图片预览





文档简介
1.4 用一元二次方程解决问题
第1课时 数字与面积问题
许多实际问题可通过建立一元二次方程数学模型求解,然后回到实际问题中进行解释和检验,列一元二次方程解决实际问题的步骤可归结为六个字:
(1) 设:用字母x(或其他字母)表示未知数;(2) 找:找出题目所涉及的各个量之间的相等关系;(3) 列:列出方程;(4) 解:解所列方程;(5) 验:检验解出的数值是不是方程的解,检验方程的解是否符合实际情况;(6) 答:书写答案.
建议用时:20分钟
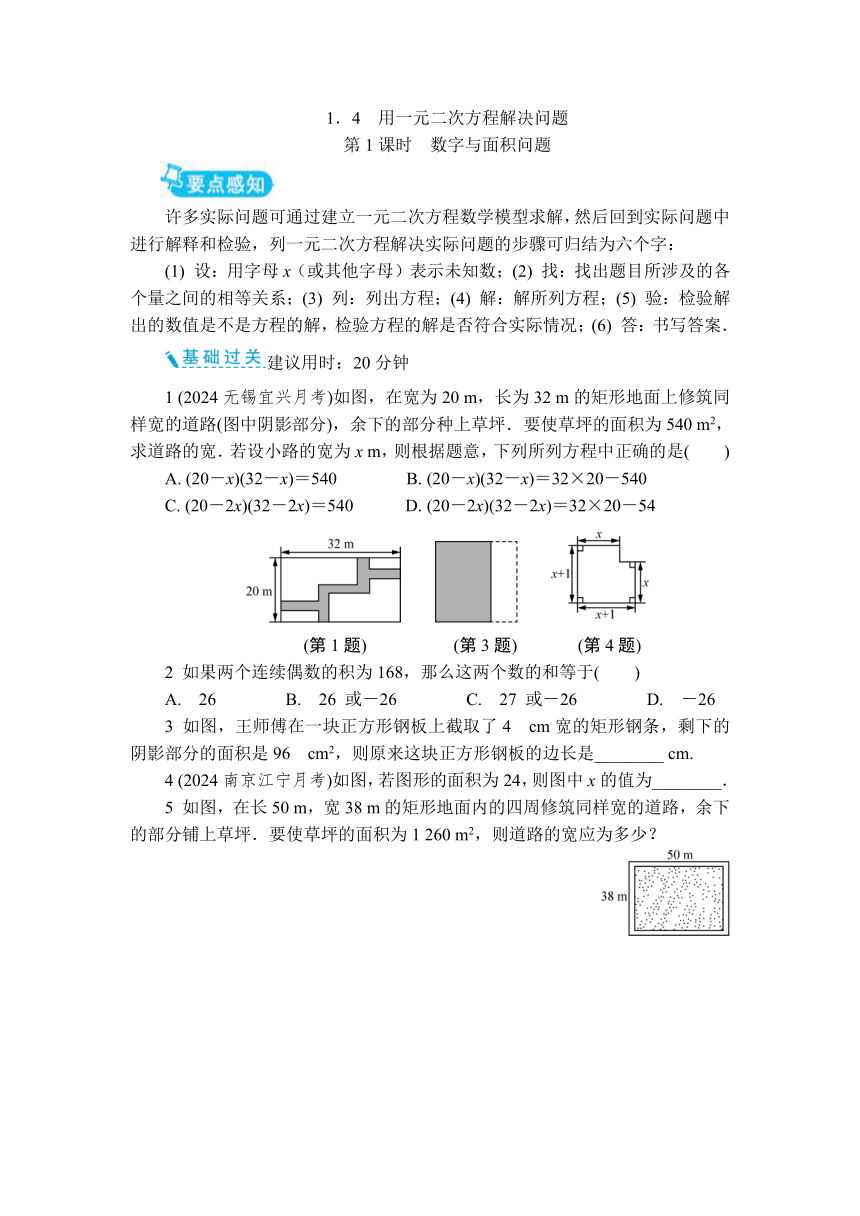
1 (2024无锡宜兴月考)如图,在宽为20 m,长为32 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540 m2,求道路的宽.若设小路的宽为x m,则根据题意,下列所列方程中正确的是( )
A. (20-x)(32-x)=540 B. (20-x)(32-x)=32×20-540
C. (20-2x)(32-2x)=540 D. (20-2x)(32-2x)=32×20-54
(第1题) (第3题) (第4题)
2 如果两个连续偶数的积为168,那么这两个数的和等于( )
A. 26 B. 26 或-26 C. 27 或-26 D. -26
3 如图,王师傅在一块正方形钢板上截取了4 cm宽的矩形钢条,剩下的阴影部分的面积是96 cm2,则原来这块正方形钢板的边长是________ cm.
4 (2024南京江宁月考)如图,若图形的面积为24,则图中x的值为________.
5 如图,在长50 m,宽38 m的矩形地面内的四周修筑同样宽的道路,余下的部分铺上草坪.要使草坪的面积为1 260 m2,则道路的宽应为多少?
6 一个两位数的个位数字比十位数字大1,如果将个位数字与十位数字对调,那么所得的两位数与原数的积比原数的平方大108,求这个两位数.
7 端午节是中国民间的传统节日,已有两千多年的历史.如图,在该月日历表上可以用一个方框圈出四个数,若将圈出的四个数按从小到大排列,中间两数的乘积为112,求这两个数.
建议用时:25+5分钟
8 (2024镇江期中)公元9世纪,阿拉伯数学家花拉子米在其著作《代数学》中提到构造图形来寻找某个一元二次方程的解方法:先构造边长为x的正方形ABCD,再分别以BC,CD为边做另一边长5的长方形,最后得到四边形AIFH是面积为64的正方形,如图所示,则下列一元二次方程中满足花拉子米寻找的解的是( )
A. x2+10x=25 B. x2+10x=64 C. x2+10x=39 D. x2+10x=89
(第8题) (第9题) (第10题)
9 如图,在长为100 m,宽为50 m的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是3 600 m2,则小路的宽是________m.
10 如图,把长为40 cm,宽为30 cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),把剩余部分折成一个有盖的长方体盒子,记剪掉的小的正方形边长为x cm(纸板的厚度忽略不计),若折成的长方体盒子表面积为950 cm2,则此时长方体盒子的体积为________cm3.
11 (2024常州期末)如图,某小区内有一块长20 m、宽18 m的矩形空地,物业打算在空地内铺设两条同样宽度的鹅卵石道路,余下部分铺上草坪.若草坪的面积为288 m2,求道路的宽度.
12 小林准备进行如下操作:把一根长为40 cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1) 要使这两个正方形的面积之和等于52 cm2,小林该怎么剪?
(2) 小峰对小林说:“这两个正方形的面积之和不可能等于44 cm2.”他的说法对吗?请说明理由.
13 某校计划利用如图所示的直角墙角(阴影部分,两边足够长),用20 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,AD两边).
(1) 若花园的面积为75 m2,求AB的长;
(2) 若在直角墙角内点P处有一棵桂花树,且到墙CD的距离为12 m,若要将这棵树围在矩形花园内(含边界,不考虑树的粗细),问该花园的面积能否为100 m2?若能,求出AB的长;若不能,请说明理由.
第2课时 增长率与计数问题
某商品经过连续两次降价(或涨价),每件售价由原来的a元降到(或涨到)了b元,设平均每次降价(或涨价)的百分率为x,则可列方程为a(1-x)2=b(或a(1+x)2=b).
建议用时:20分钟
1 (2024南通)红星村种的水稻2021年平均每公顷产7 200 kg,2023年平均每公顷产8 450 kg.求水稻每公顷产量的年平均增长率.设水稻每公顷产量的年平均增长率为x,则下列方程中正确的是( )
A. 7 200(1+x)2=8 450 B. 7 200(1+2x)=8 450
C. 8 450(1-x)2=7 200 D. 8 450(1-2x)=7 200
2 (2024南京栖霞月考)某校七年级组织一次篮球赛,各班均组队参赛,赛制为每两班之间赛两场,共需安排42场比赛.设七年级共有x个班,则下列方程中正确的是( )
A. x(x-1)=42 B. x(x+1)=42
C. x(x+1)=42 D. x(x-1)=42
3 张师傅去年开了一家超市,今年2月份开始盈利,3月份盈利5 000元,5月份盈利7 200元,从3月到5月,每月盈利的平均增长率都相同,则每月盈利的平均增长率是________.
4 某次商品交易会上,所有参加会议的任意两个商家之间都签订了一份合同,共签订合同45份,则共有________个商家参加了交易会.
5 (2024建邺区期末)我国通过药品集中采购,大大减轻了百姓的医药负担.某种药品经过两次降价,药价从每盒200元下调至72元,平均每次降价的百分率是多少?
6 某地有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
7 某校团体操表演队伍有6行8列,后又增加了51人,使得团体操表演队伍增加的行数、列数相同,求增加了多少行或多少列?
8 (2024连云港东海期中)某品牌服装店以900元/件的价格销售一款服装,“双11”期间,服装店连续两次下调销售价格后,最终以729元/件的价格销售该款服装.
(1) 求平均每次下调的百分率;
(2) 小明给服装店提出如下建议:先公布下调5%,再下调15%,这样更有吸引力,请问小明建议的方案对购买者是否更优惠?为什么?
建议用时:25+5分钟
9 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分枝,主干、枝干和小分枝的总数是43,则这种植物每个枝干长出的小分枝个数是( )
A. 4 B. 5 C. 6 D. 7
10 (2024常州期中)俗语有云:“一天不练手脚慢,两天不练丢一半,三天不练门外汉,四天不练瞪眼看.”其意思是知识和技艺在学习后,如果不及时复习,那么学习过的东西就会被遗忘.假设每天“遗忘”的百分比是一样的,根据“两天不练丢一半”,则每天“遗忘”的百分比约为(参考数据:≈1.414)( )
A. 20.3% B. 25.2% C. 29.3% D. 50%
11 (2024无锡锡山月考)电脑病毒传播速度快,如果一台电脑被感染,那么经过两轮感染后就会有121台电脑被感染,若每轮感染中平均一台电脑会感染x台电脑,则x=________.
12 (2024苏州工业园区月考)“秋风起,蟹脚痒”,随着大闸蟹的大量上市,某大闸蟹销售公司前三个月的月销售利润逐月增长,第1个月的销售利润为20万元,第3个月的销售利润为28.8万元.假设从第1个月到第3个月每月销售利润的平均增长率相同.
(1) 求从第1个月到第3个月每月销售利润的平均增长率;
(2) 进入第4个月,大闸蟹产量逐渐下降,第4个月的销售利润比第3个月的销售利润下降了20%,求从第1个月到第4个月的销售利润之和.
13 我们知道,计算n边形的对角线条数公式为n(n-3).如果一个n边形共有20条对角线,那么可以得到方程n(n-3)=20.解得n=8或n=-5(舍去),所以这个n边形是八边形.根据以上内容,问:
(1) 若一个多边形共有9条对角线,求这个多边形的边数;
(2) 小明说:“我求得一个n边形共有10条对角线”,你认为小明同学的说法正确吗?为什么?
14 “民以食为天,食以粮为先”,粮食安全事关国计民生.为了确保粮食安全,优选品种,某农业科技公司对原有小麦进行改良种植研究,在保持种植面积不变的情况下,今年小麦平均亩产量在去年的基础上增加了a%,每千克售价也在去年的基础上上涨了2a%,全部售出后总收入将增加15.5%.
(1) 求a的值;
(2) 如果明年的种植面积仍然不变,预计明年小麦平均亩产量将在今年的基础上增加a%,每千克售价将在今年的基础上上涨a%,求全部售出后明年的总收入将在今年的基础上增加的百分数.
第3课时 市场营销问题
在市场销售中,单件商品的利润、进价与售价之间存在的相等关系式为:利润=售价-进价;总利润、单件商品的利润与销售量之间的相等关系式为:总利润=单件商品的利润×销售的商品件数.
建议用时:20分钟
1 某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株的盈利为4元.若每盆增加1株,则平均每株的盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A. (x+1)(4-0.5x)=15 B. (x+3)(4+0.5x)=15
C. (x+4)(3-0.5x)=15 D. (3+x)(4-0.5x)=15
2 (2024常州新北月考)某超市销售一种饮料,平均每天可售出100箱,每箱利润为12元,为扩大销量,增加利润,超市准备适当降价,据测算,每箱每降价1元平均每天可多售出20箱,若要使每天销售饮料获利1 440元,则每箱应降价________元.
3 (2024泰州期末)某品牌纪念品每套成本为30元,当售价为40元时,平均每天的销售量为500套,经试销统计发现,如果该品牌纪念品的售价每上涨1元,那么平均每天的销售量将减少10套.为了维护消费者利益,物价部门规定:该品牌纪念品售价不能超过进价的200%,设这种纪念品每套上涨x元.
(1) 平均每天的销售量为________套(用含x的代数式表示);
(2) 商家想要使这种纪念品的销售利润平均每天达到8 000元,求每套纪念品应定价多少元?
4 某市茶叶专卖店销售某品牌茶叶,其进价为每千克240元,按每千克400元出售,平均每周可售出200 kg,后来经过市场调查发现,每降低10元/kg,则平均每周的销售量可增加40 kg,若该专卖店销售这种品牌茶叶要想平均每周获利41 600元,请回答:
(1) 每千克茶叶应降价多少元?
(2) 在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该品牌茶叶应按原售价的几折出售?
5 某商店购进600个旅游纪念品,进价为每个6元.第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1 250元,那么第二周每个旅游纪念品的销售价格为多少元?
6 某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产56件,每件的利润为10元.调查表明:每生产高一个档次的蛋糕产品,该产品每件的利润增加2元.
(1) 若生产的某批次蛋糕每件的利润为16元,此批次蛋糕提高了几个档次?属于第几档次的产品?
(2) 由于生产工序不同,蛋糕产品每提高一个档次,一天的产量会减少4件.若生产的某档次产品一天的总利润为720元,为尽量提高档次,该烘焙店生产的是第几档次的产品?
7 某商店销售甲、乙两种商品,甲的成本为5元/个,乙的成本为7元/个.甲现在的售价为10元/个,每天卖出30个,售价每提高1元,每天少卖出2个;乙现在的售价为14元/个,每天卖出6个,售价每降低1元,每天多卖出4个.假定甲、乙两种商品每天卖出的数量和不变(和为36个),且售价均为整数.
(1) 当甲的售价提高x元时,乙的售价为________元(用含x的代数式表示);
(2) 当甲的售价提高多少元时,销售这两种商品当天的总利润是268元?
第4课时 质点运动问题
1. 涉及几何图形的问题,根据图形的相关性质,灵活地找出相等关系,从而建立适当的方程解决问题.特别要注意的是,对于求得的方程的解要能够根据实际意义进行检验,选择符合实际意义的正确答案.
2. 根据实际问题建立的一元二次方程,若该方程有解,则需要检验后说明实际问题是否有符合条件的答案;若该方程没有解,则说明实际问题没有符合条件的答案.
建议用时:20分钟
1 如图,甲自西向东以4 m/s的速度行进,乙由南向北以3 m/s的速度行进,当乙到达点O时,甲已到达点O以东16 m处,如果两人继续前进,求两人相距39 m时各自的位置.
2 (2024宿迁泗洪期中)如图,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A出发,沿AB以1 cm/s的速度向点B匀速移动,同时点Q从点B出发,沿BC以2 cm/s的速度向点C匀速移动,设运动的时间为t s.
(1) PB=________cm,QC=________cm;
(2) 当t为何值时,△DPQ的面积等于28 cm2
3 如图,在△ABC中,∠C=90°,AC=6 cm,BC=8 cm,点P从点A出发沿边AC向点C以1 cm/s的速度移动,点Q从点C出发沿边CB向点B以2 cm/s的速度移动.
(1) 若P,Q两点同时出发,则几秒后可使△PQC的面积为8 cm2
(2) 若P,Q两点同时出发,则几秒后PQ的长度为 cm
(3) △PCQ的面积能否等于△ABC面积的一半?若能,求出运动的时间;若不能,请说明理由.
建议用时:25+5分钟
4 如图,长方形草坪ABCD的长AD为40 m,宽AB为30 m,草坪内有3条直的道路EC,EF和FC,ED=AF.小丽在点E处沿E→D→C方向步行,与此同时小明在点F处沿FC方向以相同的速度步行,经过26 s后两人刚好在点C处相遇,求小明步行的速度.
5 某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A,B,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(单位:cm)与时间t(单位:s)满足关系式l=t2+3t(t≥0),乙以8 cm/s的速度匀速运动,半圆的长度为42 cm.
(1) 甲运动4 s后的路程是多少?
(2) 甲、乙从开始运动到第一次相遇时,它们运动了多少秒?
(3) 甲、乙从开始运动到第二次相遇时,它们运动了多少秒?
6 如图,菱形ABCD的对角线AC,BD交于点O,AC=16 cm,BD=12 cm,动点M从点A出发沿AC方向以2 cm/s的速度运动到点C,动点N从点B出发沿BD方向以1 cm/s的速度运动到点D.若点M,N同时出发,其中一个点停止运动时,另一个点也停止运动.
(1) 出发1 s后,△MON的面积为________cm2;
(2) 出发几秒后,△MON的面积为1 cm2
1.4 用一元二次方程解决问题
第1课时 数字与面积问题
1. A 2. B 3. 12 4. 4
5. 解:设道路的宽为x m.
根据题意,得(50-2x)(38-2x)=1 260,
解得x1=4,x2=40(不符合题意,舍去).
答:道路的宽应为4 m.
6. 解:设这个数的个位数字为x,则十位数字为x-1.
根据题意,得(10x+x-1)[10(x-1)+x]-108=[10(x-1)+x]2,
解得x=2.
答:这个两位数是12.
7. 解:设方框圈出四个数中最小的为x,则中间两个数分别是x+1,x+7.
根据题意,得(x+1)(x+7)=112,
解得x1=7,x2=-15(不符合题意,舍去),
所以x+1=7+1=8,x+7=7+7=14.
答:这两个数为8和14.
8. C 9. 5 10. 1 500
11. 解:设道路的宽度为x m,则草坪的长为(20-x)m,宽为(18-x)m,
根据题意,得(20-x)(18-x)=288,
整理,得x2-38x+72=0,
解得x1=2,x2=36(不符合题意,舍去),
答:道路的宽度为2 m.
12. 解:(1) 设剪成的较短的铁丝为x cm,则较长的铁丝为(40-x)cm.
根据题意,得()2+()2=52,
解得x1=16,x2=24.
当x=16时,较长的铁丝为40-16=24;
当x=24时,较长的铁丝为40-24=16<24(舍去),
所以较短的铁丝为16 cm,较长的铁丝为24 cm.
(2) 小峰的说法正确.理由如下:
设剪成的较短的铁丝为m cm,则较长的铁丝为(40-m)cm.
根据题意,得()2+()2=44,
化简,得m2-40m+448=0.
因为b2-4ac=-192<0,所以原方程无解,
所以小峰的说法正确,这两个正方形的面积之和不可能等于44 cm2.
13. 解:(1) 设AB=x m,则x(20-x)=75,
解得x1=5,x2=15,
故AB的长为5 m或15 m.
(2) 假设将这棵树围在矩形花园内,面积能为100 m2.
设AD的长为y m,则y(20-y)=100,解得y=10.
因为10<12,
故将这棵树围在矩形花园内,花园的面积不能为100 m2.
第2课时 增长率与计数问题
1. A 2. A 3. 20% 4. 10
5. 解:设平均每次降价的百分率是x,
由题意,得200(1-x)2=72,
解得x1=0.4=40%,x2=1.6(不合题意,舍去),
答:平均每次降价的百分率是40%.
6. 解:设每轮传染中平均每个人传染了x人,
由题意,得1+x+x(1+x)=121,
解得x=10或x=-12(不合题意,舍去).
答:每轮传染中平均一个人传染了10个人.
7. 解:设增加了x行,则增加的列数为x.
根据题意,得(6+x)(8+x)-6×8=51,
整理,得x2+14x-51=0,
解得x1=3,x2=-17(不符合题意,舍去).
答:增加了3行3列.
8. 解:(1) 设平均每次下调的百分率为x,
则根据题意,得900(1-x)2=729,
解得x1=0.1=10%,x2=1.9(不符合题意,舍去),
答:平均每次下调10%.
(2) 小明建议的方案对购买者更优惠.理由如下:
根据题意,得900×(1-5%)(1-15%)=726.75.
因为726.75<729,
所以小明建议的方案对购买者更优惠.
9. C 10. C 11. 10
12 解:(1) 设从第1个月到第3个月每月销售利润的平均增长率为x.
因为第1个月的销售利润为20万元,第3个月的销售利润为28.8万元.
所以20(1+x)2=28.8,
解得x1=0.2=20%,x2=-2.2(舍去),
答:从第1个月到第3个月每月销售利润的平均增长率为20%.
(2) 20+20×(1+20%)+28.8+28.8×(1-20%)
=20+24+28.8+23.04
=95.84(万元).
答:从第1个月到第4个月的销售利润之和为95.84万元.
13. 解:(1) 根据题意,得n(n-3)=9,
解得n=6或n=-3(舍去),
答:这个多边形的边数是6.
(2) 小明同学的说法不正确,理由如下:
根据题意,得n(n-3)=10,
解得n=,
因为n的值不是正整数,
所以小明同学的说法不正确.
14. 解:(1) 根据题意,得(1+a%)(1+2a%)=1+15.5%,
整理,得a2+150a-775=0,
解得a1=5,a2=-155(不符合题意,舍去).
答:a的值为5.
(2) (1+5%)×(1+×5%)-1=0.134=13.4%.
答:全部售出后明年的总收入将在今年的基础上增加的百分数为13.4%.
第3课时 市场营销问题
1. D 2. 3或4
3. 解:(1) 500-10x
(2) 每套纪念品应定价为(40+x)元,平均每天的销售量为(500-10x)套,
根据题意,得(40+x-30)(500-10x)=8 000,
40+x≤30×200%,
整理,得x2-40x+300=0,x≤20,
解得x1=10,x2=30(不符合题意,舍去),
所以40+x=50.
答:每套纪念品应定价50元.
4. 解:(1) 设每千克茶叶应降价x元,则平均每周可售出(200+) kg.
根据题意,得(400-240-x)(200+)=41 600,
整理,得x2-110x+2 400=0,解得x1=30,x2=80.
答:每千克茶叶应降价30元或80元.
(2) 因为尽可能让利于顾客,所以x=80,
所以×10=8.
答:该品牌茶叶应按原售价的八折出售.
5. 解:由题意,得第二周每个旅游纪念品的销售价格为(10-x)元,第二周的销售量为(200+50x)个,清仓处理了600-200-(200+50x)=(200-50x)个.
根据题意,得10×200+(10-x)(200+50x)+4(200-50x)-6×600=1 250,
整理,得x2-2x+1=0,解得x1=x2=1,
所以10-x=9.
答:第二周每个旅游纪念品的销售价格为 9元.
6. 解:(1) (16-10)÷2=3(个),3+1=4.
答:提高了三个档次,属于第四档次的产品.
(2) 设提高了x个档次,则每天可生产(56-4x)件,每件的利润为(10+2x)元.
根据题意,得(10+2x)(56-4x)=720,
整理,得x2-9x+20=0,
解得x1=4,x2=5.
因为尽量提高档次,所以x=5.
答:提高了五个档次,该烘焙店生产的是第六档次的产品.
7. 解:(1) 14-
(2) 设当甲商品的售价提高x元时,销售这两种商品当天的总利润是268元,
根据题意,得(5+x)(30-2x)+(6+2x)(14--7)=268,
整理,得3x2-31x+76=0,解得x1=4,x2=.
因为售价均为整数,所以x=4.
答:当甲商品的售价提高4元时,销售这两种商品当天的总利润是268元.
第4课时 质点运动问题
1. 解:设乙到达点O后经过t s两人相距39 m.
根据题意,得(3t)2+(16+4t)2=392,
整理,得25t2+128t-1 265=0,
解得t1=5,t2=-10.12(不符合题意,舍去),
当t=5时,3t=15,16+4t=16+20=36.
答:当两人相距39 m时,甲在点O以东36 m处,乙在点O以北15 m处.
2. 解:(1) 6-t 12-2t
(2) 因为AP=t cm,QB=2t cm,PB=(6-t) cm,QC=(12-2t) cm,
根据题意,得S△DPQ=S矩形ABCD-S△APD-S△BPQ-S△DCQ=28,
所以AB·BC-AP·AD-PB·BQ-QC·CD=28,
所以12×6-×12t-×2t×(6-t)-×6×(12-2t)=28,
所以t2-6t+8=0,
解得t1=2,t2=4.
答:当t为2或4时,△DPQ的面积等于28 cm2.
3. 解:因为点P的移动速度为1 cm/s,点Q的移动速度为2 cm/s,
所以设CP=6-x,则CQ=2x.
(1) △PQC的面积为8 cm2,即(6-x)·2x=8,
解得x1=2,x2=4,
故若P,Q两点同时出发,则2 s或4 s后△PQC的面积为8 cm2.
(2) PQ的长度为 cm,即(2x)2+(6-x)2=,
解得x1=x2=1.2,
故若P,Q两点同时出发,则1.2 s后PQ的长度为 cm.
(3) 根据题意,得S△ABC=AC·BC=×6×8=24,
则×2x×(6-x)=×24,即x2-6x+12=0.
因为62-4×12=-12<0,所以该方程无实数解,
所以不存在使得△PCQ的面积等于△ABC面积的一半的时刻.
4. 解:因为四边形ABCD是矩形,
所以CD=AB=30 m,BC=AD=40 m,∠B=90°.
设DE=AF=x m,则CF=DE+CD=(x+30)m.
在Rt△BCF中,BF=AB-AF=(30-x)m,
所以(x+30)2=(30-x)2+402,
解得x=,所以CF=+30=(m),
所以小明步行的速度为÷26=(m/s).
答:小明步行的速度为 m/s.
5. 解:(1) 当t=4 s时,l=t2+3t=16+12=28(cm).
故甲运动4 s后的路程是28 cm.
(2) 由图可知,甲、乙第一次相遇时走过的总路程为半圆42 cm,甲走过的路程为 t2+3t,乙走过的路程为8t,
则t2+3t+8t=42,
解得t1=3,t2=-14(不符合题意,舍去).
故甲、乙从开始运动到第一次相遇时,它们运动了3 s.
(3) 由图可知,甲、乙第二次相遇时走过的总路程为三个半圆3×42=126(cm),
则t2+3t+8t=126,
解得t3=7,t4=-18(不符合题意,舍去).
故甲、乙从开始运动到第二次相遇时,它们运动了7 s.
6. 解:(1) 15
(2) 设出发t s后,△MON的面积为1 cm2,则AM=2t,BN=t.
当点M在AO上,点N在BO上时,即0≤t≤4,
则MO=8-2t,NO=6-t,
所以×(8-2t)×(6-t)=1,
解得t1=5+(不符合题意,舍去),t2=5-;
当点M在OC上,点N在BO上时,即4<t≤6,
则MO=2t-8,NO=6-t,
所以×(2t-8)×(6-t)=1,解得t3=t4=5;
当点M在OC上,点N在OD上时,即6<t≤8,
则MO=2t-8,NO=t-6,
所以×(2t-8)×(t-6)=1,
解得t5=5+,t6=5-(不符合题意,舍去).
综上,出发(5+)s或(5-)s或5 s后,△MON的面积为1 cm2.
第1课时 数字与面积问题
许多实际问题可通过建立一元二次方程数学模型求解,然后回到实际问题中进行解释和检验,列一元二次方程解决实际问题的步骤可归结为六个字:
(1) 设:用字母x(或其他字母)表示未知数;(2) 找:找出题目所涉及的各个量之间的相等关系;(3) 列:列出方程;(4) 解:解所列方程;(5) 验:检验解出的数值是不是方程的解,检验方程的解是否符合实际情况;(6) 答:书写答案.
建议用时:20分钟
1 (2024无锡宜兴月考)如图,在宽为20 m,长为32 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540 m2,求道路的宽.若设小路的宽为x m,则根据题意,下列所列方程中正确的是( )
A. (20-x)(32-x)=540 B. (20-x)(32-x)=32×20-540
C. (20-2x)(32-2x)=540 D. (20-2x)(32-2x)=32×20-54
(第1题) (第3题) (第4题)
2 如果两个连续偶数的积为168,那么这两个数的和等于( )
A. 26 B. 26 或-26 C. 27 或-26 D. -26
3 如图,王师傅在一块正方形钢板上截取了4 cm宽的矩形钢条,剩下的阴影部分的面积是96 cm2,则原来这块正方形钢板的边长是________ cm.
4 (2024南京江宁月考)如图,若图形的面积为24,则图中x的值为________.
5 如图,在长50 m,宽38 m的矩形地面内的四周修筑同样宽的道路,余下的部分铺上草坪.要使草坪的面积为1 260 m2,则道路的宽应为多少?
6 一个两位数的个位数字比十位数字大1,如果将个位数字与十位数字对调,那么所得的两位数与原数的积比原数的平方大108,求这个两位数.
7 端午节是中国民间的传统节日,已有两千多年的历史.如图,在该月日历表上可以用一个方框圈出四个数,若将圈出的四个数按从小到大排列,中间两数的乘积为112,求这两个数.
建议用时:25+5分钟
8 (2024镇江期中)公元9世纪,阿拉伯数学家花拉子米在其著作《代数学》中提到构造图形来寻找某个一元二次方程的解方法:先构造边长为x的正方形ABCD,再分别以BC,CD为边做另一边长5的长方形,最后得到四边形AIFH是面积为64的正方形,如图所示,则下列一元二次方程中满足花拉子米寻找的解的是( )
A. x2+10x=25 B. x2+10x=64 C. x2+10x=39 D. x2+10x=89
(第8题) (第9题) (第10题)
9 如图,在长为100 m,宽为50 m的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是3 600 m2,则小路的宽是________m.
10 如图,把长为40 cm,宽为30 cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),把剩余部分折成一个有盖的长方体盒子,记剪掉的小的正方形边长为x cm(纸板的厚度忽略不计),若折成的长方体盒子表面积为950 cm2,则此时长方体盒子的体积为________cm3.
11 (2024常州期末)如图,某小区内有一块长20 m、宽18 m的矩形空地,物业打算在空地内铺设两条同样宽度的鹅卵石道路,余下部分铺上草坪.若草坪的面积为288 m2,求道路的宽度.
12 小林准备进行如下操作:把一根长为40 cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1) 要使这两个正方形的面积之和等于52 cm2,小林该怎么剪?
(2) 小峰对小林说:“这两个正方形的面积之和不可能等于44 cm2.”他的说法对吗?请说明理由.
13 某校计划利用如图所示的直角墙角(阴影部分,两边足够长),用20 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,AD两边).
(1) 若花园的面积为75 m2,求AB的长;
(2) 若在直角墙角内点P处有一棵桂花树,且到墙CD的距离为12 m,若要将这棵树围在矩形花园内(含边界,不考虑树的粗细),问该花园的面积能否为100 m2?若能,求出AB的长;若不能,请说明理由.
第2课时 增长率与计数问题
某商品经过连续两次降价(或涨价),每件售价由原来的a元降到(或涨到)了b元,设平均每次降价(或涨价)的百分率为x,则可列方程为a(1-x)2=b(或a(1+x)2=b).
建议用时:20分钟
1 (2024南通)红星村种的水稻2021年平均每公顷产7 200 kg,2023年平均每公顷产8 450 kg.求水稻每公顷产量的年平均增长率.设水稻每公顷产量的年平均增长率为x,则下列方程中正确的是( )
A. 7 200(1+x)2=8 450 B. 7 200(1+2x)=8 450
C. 8 450(1-x)2=7 200 D. 8 450(1-2x)=7 200
2 (2024南京栖霞月考)某校七年级组织一次篮球赛,各班均组队参赛,赛制为每两班之间赛两场,共需安排42场比赛.设七年级共有x个班,则下列方程中正确的是( )
A. x(x-1)=42 B. x(x+1)=42
C. x(x+1)=42 D. x(x-1)=42
3 张师傅去年开了一家超市,今年2月份开始盈利,3月份盈利5 000元,5月份盈利7 200元,从3月到5月,每月盈利的平均增长率都相同,则每月盈利的平均增长率是________.
4 某次商品交易会上,所有参加会议的任意两个商家之间都签订了一份合同,共签订合同45份,则共有________个商家参加了交易会.
5 (2024建邺区期末)我国通过药品集中采购,大大减轻了百姓的医药负担.某种药品经过两次降价,药价从每盒200元下调至72元,平均每次降价的百分率是多少?
6 某地有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
7 某校团体操表演队伍有6行8列,后又增加了51人,使得团体操表演队伍增加的行数、列数相同,求增加了多少行或多少列?
8 (2024连云港东海期中)某品牌服装店以900元/件的价格销售一款服装,“双11”期间,服装店连续两次下调销售价格后,最终以729元/件的价格销售该款服装.
(1) 求平均每次下调的百分率;
(2) 小明给服装店提出如下建议:先公布下调5%,再下调15%,这样更有吸引力,请问小明建议的方案对购买者是否更优惠?为什么?
建议用时:25+5分钟
9 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分枝,主干、枝干和小分枝的总数是43,则这种植物每个枝干长出的小分枝个数是( )
A. 4 B. 5 C. 6 D. 7
10 (2024常州期中)俗语有云:“一天不练手脚慢,两天不练丢一半,三天不练门外汉,四天不练瞪眼看.”其意思是知识和技艺在学习后,如果不及时复习,那么学习过的东西就会被遗忘.假设每天“遗忘”的百分比是一样的,根据“两天不练丢一半”,则每天“遗忘”的百分比约为(参考数据:≈1.414)( )
A. 20.3% B. 25.2% C. 29.3% D. 50%
11 (2024无锡锡山月考)电脑病毒传播速度快,如果一台电脑被感染,那么经过两轮感染后就会有121台电脑被感染,若每轮感染中平均一台电脑会感染x台电脑,则x=________.
12 (2024苏州工业园区月考)“秋风起,蟹脚痒”,随着大闸蟹的大量上市,某大闸蟹销售公司前三个月的月销售利润逐月增长,第1个月的销售利润为20万元,第3个月的销售利润为28.8万元.假设从第1个月到第3个月每月销售利润的平均增长率相同.
(1) 求从第1个月到第3个月每月销售利润的平均增长率;
(2) 进入第4个月,大闸蟹产量逐渐下降,第4个月的销售利润比第3个月的销售利润下降了20%,求从第1个月到第4个月的销售利润之和.
13 我们知道,计算n边形的对角线条数公式为n(n-3).如果一个n边形共有20条对角线,那么可以得到方程n(n-3)=20.解得n=8或n=-5(舍去),所以这个n边形是八边形.根据以上内容,问:
(1) 若一个多边形共有9条对角线,求这个多边形的边数;
(2) 小明说:“我求得一个n边形共有10条对角线”,你认为小明同学的说法正确吗?为什么?
14 “民以食为天,食以粮为先”,粮食安全事关国计民生.为了确保粮食安全,优选品种,某农业科技公司对原有小麦进行改良种植研究,在保持种植面积不变的情况下,今年小麦平均亩产量在去年的基础上增加了a%,每千克售价也在去年的基础上上涨了2a%,全部售出后总收入将增加15.5%.
(1) 求a的值;
(2) 如果明年的种植面积仍然不变,预计明年小麦平均亩产量将在今年的基础上增加a%,每千克售价将在今年的基础上上涨a%,求全部售出后明年的总收入将在今年的基础上增加的百分数.
第3课时 市场营销问题
在市场销售中,单件商品的利润、进价与售价之间存在的相等关系式为:利润=售价-进价;总利润、单件商品的利润与销售量之间的相等关系式为:总利润=单件商品的利润×销售的商品件数.
建议用时:20分钟
1 某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株的盈利为4元.若每盆增加1株,则平均每株的盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A. (x+1)(4-0.5x)=15 B. (x+3)(4+0.5x)=15
C. (x+4)(3-0.5x)=15 D. (3+x)(4-0.5x)=15
2 (2024常州新北月考)某超市销售一种饮料,平均每天可售出100箱,每箱利润为12元,为扩大销量,增加利润,超市准备适当降价,据测算,每箱每降价1元平均每天可多售出20箱,若要使每天销售饮料获利1 440元,则每箱应降价________元.
3 (2024泰州期末)某品牌纪念品每套成本为30元,当售价为40元时,平均每天的销售量为500套,经试销统计发现,如果该品牌纪念品的售价每上涨1元,那么平均每天的销售量将减少10套.为了维护消费者利益,物价部门规定:该品牌纪念品售价不能超过进价的200%,设这种纪念品每套上涨x元.
(1) 平均每天的销售量为________套(用含x的代数式表示);
(2) 商家想要使这种纪念品的销售利润平均每天达到8 000元,求每套纪念品应定价多少元?
4 某市茶叶专卖店销售某品牌茶叶,其进价为每千克240元,按每千克400元出售,平均每周可售出200 kg,后来经过市场调查发现,每降低10元/kg,则平均每周的销售量可增加40 kg,若该专卖店销售这种品牌茶叶要想平均每周获利41 600元,请回答:
(1) 每千克茶叶应降价多少元?
(2) 在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该品牌茶叶应按原售价的几折出售?
5 某商店购进600个旅游纪念品,进价为每个6元.第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1 250元,那么第二周每个旅游纪念品的销售价格为多少元?
6 某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产56件,每件的利润为10元.调查表明:每生产高一个档次的蛋糕产品,该产品每件的利润增加2元.
(1) 若生产的某批次蛋糕每件的利润为16元,此批次蛋糕提高了几个档次?属于第几档次的产品?
(2) 由于生产工序不同,蛋糕产品每提高一个档次,一天的产量会减少4件.若生产的某档次产品一天的总利润为720元,为尽量提高档次,该烘焙店生产的是第几档次的产品?
7 某商店销售甲、乙两种商品,甲的成本为5元/个,乙的成本为7元/个.甲现在的售价为10元/个,每天卖出30个,售价每提高1元,每天少卖出2个;乙现在的售价为14元/个,每天卖出6个,售价每降低1元,每天多卖出4个.假定甲、乙两种商品每天卖出的数量和不变(和为36个),且售价均为整数.
(1) 当甲的售价提高x元时,乙的售价为________元(用含x的代数式表示);
(2) 当甲的售价提高多少元时,销售这两种商品当天的总利润是268元?
第4课时 质点运动问题
1. 涉及几何图形的问题,根据图形的相关性质,灵活地找出相等关系,从而建立适当的方程解决问题.特别要注意的是,对于求得的方程的解要能够根据实际意义进行检验,选择符合实际意义的正确答案.
2. 根据实际问题建立的一元二次方程,若该方程有解,则需要检验后说明实际问题是否有符合条件的答案;若该方程没有解,则说明实际问题没有符合条件的答案.
建议用时:20分钟
1 如图,甲自西向东以4 m/s的速度行进,乙由南向北以3 m/s的速度行进,当乙到达点O时,甲已到达点O以东16 m处,如果两人继续前进,求两人相距39 m时各自的位置.
2 (2024宿迁泗洪期中)如图,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A出发,沿AB以1 cm/s的速度向点B匀速移动,同时点Q从点B出发,沿BC以2 cm/s的速度向点C匀速移动,设运动的时间为t s.
(1) PB=________cm,QC=________cm;
(2) 当t为何值时,△DPQ的面积等于28 cm2
3 如图,在△ABC中,∠C=90°,AC=6 cm,BC=8 cm,点P从点A出发沿边AC向点C以1 cm/s的速度移动,点Q从点C出发沿边CB向点B以2 cm/s的速度移动.
(1) 若P,Q两点同时出发,则几秒后可使△PQC的面积为8 cm2
(2) 若P,Q两点同时出发,则几秒后PQ的长度为 cm
(3) △PCQ的面积能否等于△ABC面积的一半?若能,求出运动的时间;若不能,请说明理由.
建议用时:25+5分钟
4 如图,长方形草坪ABCD的长AD为40 m,宽AB为30 m,草坪内有3条直的道路EC,EF和FC,ED=AF.小丽在点E处沿E→D→C方向步行,与此同时小明在点F处沿FC方向以相同的速度步行,经过26 s后两人刚好在点C处相遇,求小明步行的速度.
5 某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A,B,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(单位:cm)与时间t(单位:s)满足关系式l=t2+3t(t≥0),乙以8 cm/s的速度匀速运动,半圆的长度为42 cm.
(1) 甲运动4 s后的路程是多少?
(2) 甲、乙从开始运动到第一次相遇时,它们运动了多少秒?
(3) 甲、乙从开始运动到第二次相遇时,它们运动了多少秒?
6 如图,菱形ABCD的对角线AC,BD交于点O,AC=16 cm,BD=12 cm,动点M从点A出发沿AC方向以2 cm/s的速度运动到点C,动点N从点B出发沿BD方向以1 cm/s的速度运动到点D.若点M,N同时出发,其中一个点停止运动时,另一个点也停止运动.
(1) 出发1 s后,△MON的面积为________cm2;
(2) 出发几秒后,△MON的面积为1 cm2
1.4 用一元二次方程解决问题
第1课时 数字与面积问题
1. A 2. B 3. 12 4. 4
5. 解:设道路的宽为x m.
根据题意,得(50-2x)(38-2x)=1 260,
解得x1=4,x2=40(不符合题意,舍去).
答:道路的宽应为4 m.
6. 解:设这个数的个位数字为x,则十位数字为x-1.
根据题意,得(10x+x-1)[10(x-1)+x]-108=[10(x-1)+x]2,
解得x=2.
答:这个两位数是12.
7. 解:设方框圈出四个数中最小的为x,则中间两个数分别是x+1,x+7.
根据题意,得(x+1)(x+7)=112,
解得x1=7,x2=-15(不符合题意,舍去),
所以x+1=7+1=8,x+7=7+7=14.
答:这两个数为8和14.
8. C 9. 5 10. 1 500
11. 解:设道路的宽度为x m,则草坪的长为(20-x)m,宽为(18-x)m,
根据题意,得(20-x)(18-x)=288,
整理,得x2-38x+72=0,
解得x1=2,x2=36(不符合题意,舍去),
答:道路的宽度为2 m.
12. 解:(1) 设剪成的较短的铁丝为x cm,则较长的铁丝为(40-x)cm.
根据题意,得()2+()2=52,
解得x1=16,x2=24.
当x=16时,较长的铁丝为40-16=24;
当x=24时,较长的铁丝为40-24=16<24(舍去),
所以较短的铁丝为16 cm,较长的铁丝为24 cm.
(2) 小峰的说法正确.理由如下:
设剪成的较短的铁丝为m cm,则较长的铁丝为(40-m)cm.
根据题意,得()2+()2=44,
化简,得m2-40m+448=0.
因为b2-4ac=-192<0,所以原方程无解,
所以小峰的说法正确,这两个正方形的面积之和不可能等于44 cm2.
13. 解:(1) 设AB=x m,则x(20-x)=75,
解得x1=5,x2=15,
故AB的长为5 m或15 m.
(2) 假设将这棵树围在矩形花园内,面积能为100 m2.
设AD的长为y m,则y(20-y)=100,解得y=10.
因为10<12,
故将这棵树围在矩形花园内,花园的面积不能为100 m2.
第2课时 增长率与计数问题
1. A 2. A 3. 20% 4. 10
5. 解:设平均每次降价的百分率是x,
由题意,得200(1-x)2=72,
解得x1=0.4=40%,x2=1.6(不合题意,舍去),
答:平均每次降价的百分率是40%.
6. 解:设每轮传染中平均每个人传染了x人,
由题意,得1+x+x(1+x)=121,
解得x=10或x=-12(不合题意,舍去).
答:每轮传染中平均一个人传染了10个人.
7. 解:设增加了x行,则增加的列数为x.
根据题意,得(6+x)(8+x)-6×8=51,
整理,得x2+14x-51=0,
解得x1=3,x2=-17(不符合题意,舍去).
答:增加了3行3列.
8. 解:(1) 设平均每次下调的百分率为x,
则根据题意,得900(1-x)2=729,
解得x1=0.1=10%,x2=1.9(不符合题意,舍去),
答:平均每次下调10%.
(2) 小明建议的方案对购买者更优惠.理由如下:
根据题意,得900×(1-5%)(1-15%)=726.75.
因为726.75<729,
所以小明建议的方案对购买者更优惠.
9. C 10. C 11. 10
12 解:(1) 设从第1个月到第3个月每月销售利润的平均增长率为x.
因为第1个月的销售利润为20万元,第3个月的销售利润为28.8万元.
所以20(1+x)2=28.8,
解得x1=0.2=20%,x2=-2.2(舍去),
答:从第1个月到第3个月每月销售利润的平均增长率为20%.
(2) 20+20×(1+20%)+28.8+28.8×(1-20%)
=20+24+28.8+23.04
=95.84(万元).
答:从第1个月到第4个月的销售利润之和为95.84万元.
13. 解:(1) 根据题意,得n(n-3)=9,
解得n=6或n=-3(舍去),
答:这个多边形的边数是6.
(2) 小明同学的说法不正确,理由如下:
根据题意,得n(n-3)=10,
解得n=,
因为n的值不是正整数,
所以小明同学的说法不正确.
14. 解:(1) 根据题意,得(1+a%)(1+2a%)=1+15.5%,
整理,得a2+150a-775=0,
解得a1=5,a2=-155(不符合题意,舍去).
答:a的值为5.
(2) (1+5%)×(1+×5%)-1=0.134=13.4%.
答:全部售出后明年的总收入将在今年的基础上增加的百分数为13.4%.
第3课时 市场营销问题
1. D 2. 3或4
3. 解:(1) 500-10x
(2) 每套纪念品应定价为(40+x)元,平均每天的销售量为(500-10x)套,
根据题意,得(40+x-30)(500-10x)=8 000,
40+x≤30×200%,
整理,得x2-40x+300=0,x≤20,
解得x1=10,x2=30(不符合题意,舍去),
所以40+x=50.
答:每套纪念品应定价50元.
4. 解:(1) 设每千克茶叶应降价x元,则平均每周可售出(200+) kg.
根据题意,得(400-240-x)(200+)=41 600,
整理,得x2-110x+2 400=0,解得x1=30,x2=80.
答:每千克茶叶应降价30元或80元.
(2) 因为尽可能让利于顾客,所以x=80,
所以×10=8.
答:该品牌茶叶应按原售价的八折出售.
5. 解:由题意,得第二周每个旅游纪念品的销售价格为(10-x)元,第二周的销售量为(200+50x)个,清仓处理了600-200-(200+50x)=(200-50x)个.
根据题意,得10×200+(10-x)(200+50x)+4(200-50x)-6×600=1 250,
整理,得x2-2x+1=0,解得x1=x2=1,
所以10-x=9.
答:第二周每个旅游纪念品的销售价格为 9元.
6. 解:(1) (16-10)÷2=3(个),3+1=4.
答:提高了三个档次,属于第四档次的产品.
(2) 设提高了x个档次,则每天可生产(56-4x)件,每件的利润为(10+2x)元.
根据题意,得(10+2x)(56-4x)=720,
整理,得x2-9x+20=0,
解得x1=4,x2=5.
因为尽量提高档次,所以x=5.
答:提高了五个档次,该烘焙店生产的是第六档次的产品.
7. 解:(1) 14-
(2) 设当甲商品的售价提高x元时,销售这两种商品当天的总利润是268元,
根据题意,得(5+x)(30-2x)+(6+2x)(14--7)=268,
整理,得3x2-31x+76=0,解得x1=4,x2=.
因为售价均为整数,所以x=4.
答:当甲商品的售价提高4元时,销售这两种商品当天的总利润是268元.
第4课时 质点运动问题
1. 解:设乙到达点O后经过t s两人相距39 m.
根据题意,得(3t)2+(16+4t)2=392,
整理,得25t2+128t-1 265=0,
解得t1=5,t2=-10.12(不符合题意,舍去),
当t=5时,3t=15,16+4t=16+20=36.
答:当两人相距39 m时,甲在点O以东36 m处,乙在点O以北15 m处.
2. 解:(1) 6-t 12-2t
(2) 因为AP=t cm,QB=2t cm,PB=(6-t) cm,QC=(12-2t) cm,
根据题意,得S△DPQ=S矩形ABCD-S△APD-S△BPQ-S△DCQ=28,
所以AB·BC-AP·AD-PB·BQ-QC·CD=28,
所以12×6-×12t-×2t×(6-t)-×6×(12-2t)=28,
所以t2-6t+8=0,
解得t1=2,t2=4.
答:当t为2或4时,△DPQ的面积等于28 cm2.
3. 解:因为点P的移动速度为1 cm/s,点Q的移动速度为2 cm/s,
所以设CP=6-x,则CQ=2x.
(1) △PQC的面积为8 cm2,即(6-x)·2x=8,
解得x1=2,x2=4,
故若P,Q两点同时出发,则2 s或4 s后△PQC的面积为8 cm2.
(2) PQ的长度为 cm,即(2x)2+(6-x)2=,
解得x1=x2=1.2,
故若P,Q两点同时出发,则1.2 s后PQ的长度为 cm.
(3) 根据题意,得S△ABC=AC·BC=×6×8=24,
则×2x×(6-x)=×24,即x2-6x+12=0.
因为62-4×12=-12<0,所以该方程无实数解,
所以不存在使得△PCQ的面积等于△ABC面积的一半的时刻.
4. 解:因为四边形ABCD是矩形,
所以CD=AB=30 m,BC=AD=40 m,∠B=90°.
设DE=AF=x m,则CF=DE+CD=(x+30)m.
在Rt△BCF中,BF=AB-AF=(30-x)m,
所以(x+30)2=(30-x)2+402,
解得x=,所以CF=+30=(m),
所以小明步行的速度为÷26=(m/s).
答:小明步行的速度为 m/s.
5. 解:(1) 当t=4 s时,l=t2+3t=16+12=28(cm).
故甲运动4 s后的路程是28 cm.
(2) 由图可知,甲、乙第一次相遇时走过的总路程为半圆42 cm,甲走过的路程为 t2+3t,乙走过的路程为8t,
则t2+3t+8t=42,
解得t1=3,t2=-14(不符合题意,舍去).
故甲、乙从开始运动到第一次相遇时,它们运动了3 s.
(3) 由图可知,甲、乙第二次相遇时走过的总路程为三个半圆3×42=126(cm),
则t2+3t+8t=126,
解得t3=7,t4=-18(不符合题意,舍去).
故甲、乙从开始运动到第二次相遇时,它们运动了7 s.
6. 解:(1) 15
(2) 设出发t s后,△MON的面积为1 cm2,则AM=2t,BN=t.
当点M在AO上,点N在BO上时,即0≤t≤4,
则MO=8-2t,NO=6-t,
所以×(8-2t)×(6-t)=1,
解得t1=5+(不符合题意,舍去),t2=5-;
当点M在OC上,点N在BO上时,即4<t≤6,
则MO=2t-8,NO=6-t,
所以×(2t-8)×(6-t)=1,解得t3=t4=5;
当点M在OC上,点N在OD上时,即6<t≤8,
则MO=2t-8,NO=t-6,
所以×(2t-8)×(t-6)=1,
解得t5=5+,t6=5-(不符合题意,舍去).
综上,出发(5+)s或(5-)s或5 s后,△MON的面积为1 cm2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
