2.1 圆 同步练 (含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 2.1 圆 同步练 (含答案) 2025-2026学年数学苏科版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 349.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 00:00:00 | ||
图片预览


文档简介
2.1 圆
第1课时 圆 的 概 念
1. (1) 圆是到定点的距离等于定长的点的集合,定点就是圆心,定长就是半径;
(2) 圆上各点到圆心的距离都等于半径;到圆心的距离等于半径的点都在圆上.
2. 已知⊙O的半径为r,点P到圆心O的距离为d,则
(1) 点P在⊙O上 d=r;(2) 点P在⊙O外 d>r;(3) 点P在⊙O内 d建议用时:20分钟
1 (2024南京鼓楼月考)在△ABC中,AB=AC,若以点A为圆心,以AB为半径作圆,则点C与⊙A的位置关系为( )
A. 点C在⊙A内 B. 点C在⊙A上
C. 点C在⊙A外 D. 点C在⊙A内或⊙A外
2 (2024南京江宁月考)若⊙O的半径为3 cm,点A不在⊙O内,则OA的长( )
A. 大于3 cm B. 不小于3 cm C. 大于6 cm D. 不小于6 cm
3 在平面直角坐标系中,圆心O为坐标原点,⊙O的半径为5,则点P(3,4)与⊙O的位置关系为( )
A. 点P在⊙O上 B. 点P在⊙O外
C. 点P在⊙O内 D. 无法确定
4 早在2 000多年前的战国时期,《墨经》一书中就给出了圆的描述性定义:“圜(这里读yuan),一中同长也”这就是说,圆是平面内到定点的距离等于定长的点的集合.其中,定点是________,定长是________.
5 (2024无锡江阴月考)若⊙O的半径为4 cm,点P到圆心O的距离为5 cm,则点P与⊙O的位置关系是________.
6 (2024盐城射阳月考)到点O的距离等于7 cm的点的集合是________.
7 (2024扬州江都月考)已知⊙O的半径是8,点P到圆心O的距离d为方程x2-4x-5=0的一个根,则点P与⊙O的位置关系是________.
8 作线段AB=3 cm,按下列要求作图:
(1) 到点A的距离等于2 cm的点的集合;
(2) 到点B的距离等于1.5 cm的点的集合;
(3) 到点A的距离大于2 cm且到点B的距离小于1.5 cm的点的集合.(用阴影部分表示)
建议用时:25+5分钟
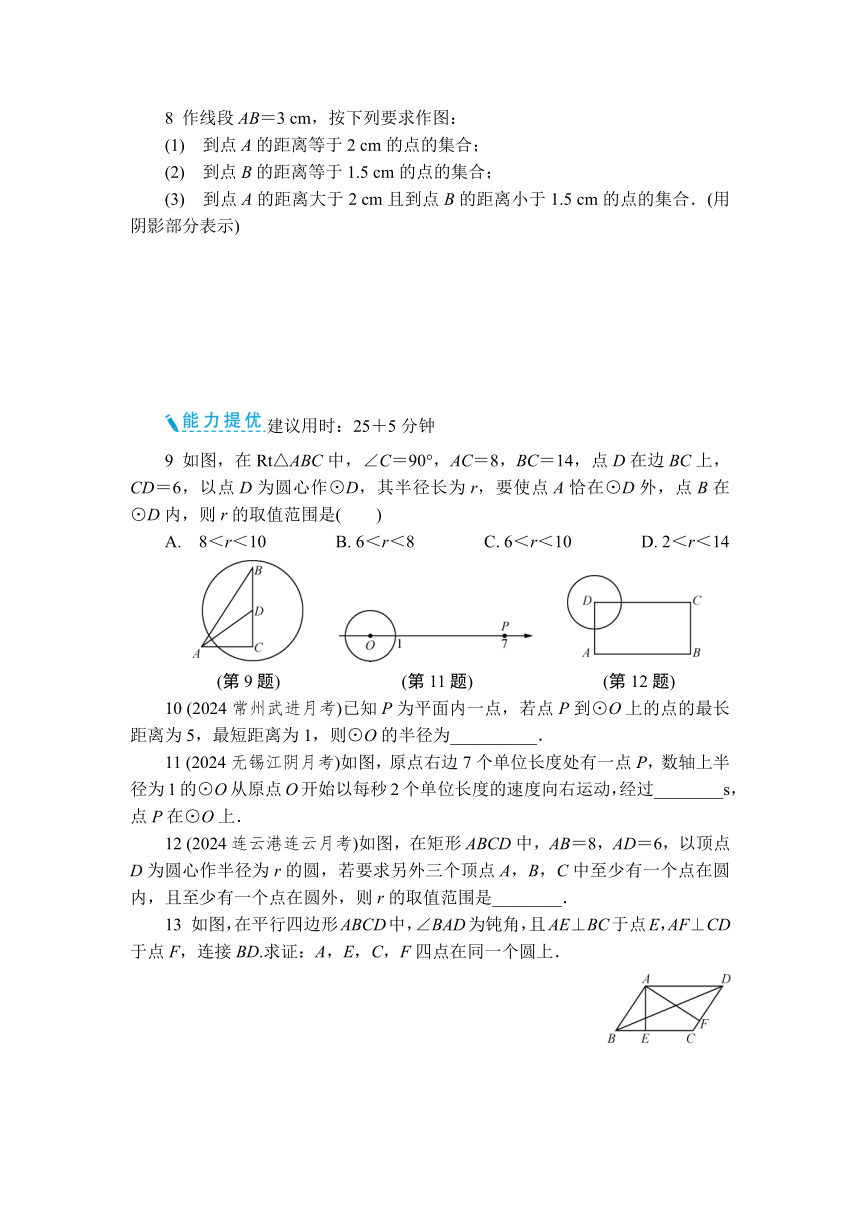
9 如图,在Rt△ABC中,∠C=90°,AC=8,BC=14,点D在边BC上,CD=6,以点D为圆心作⊙D,其半径长为r,要使点A恰在⊙D外,点B在⊙D内,则r的取值范围是( )
A. 8<r<10 B. 6<r<8 C. 6<r<10 D. 2<r<14
(第9题) (第11题) (第12题)
10 (2024常州武进月考)已知P为平面内一点,若点P到⊙O上的点的最长距离为5,最短距离为1,则⊙O的半径为__________.
11 (2024无锡江阴月考)如图,原点右边7个单位长度处有一点P,数轴上半径为1的⊙O从原点O开始以每秒2个单位长度的速度向右运动,经过________s,点P在⊙O上.
12 (2024连云港连云月考)如图,在矩形ABCD中,AB=8,AD=6,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是________.
13 如图,在平行四边形ABCD中,∠BAD为钝角,且AE⊥BC于点E,AF⊥CD于点F,连接BD.求证:A,E,C,F四点在同一个圆上.
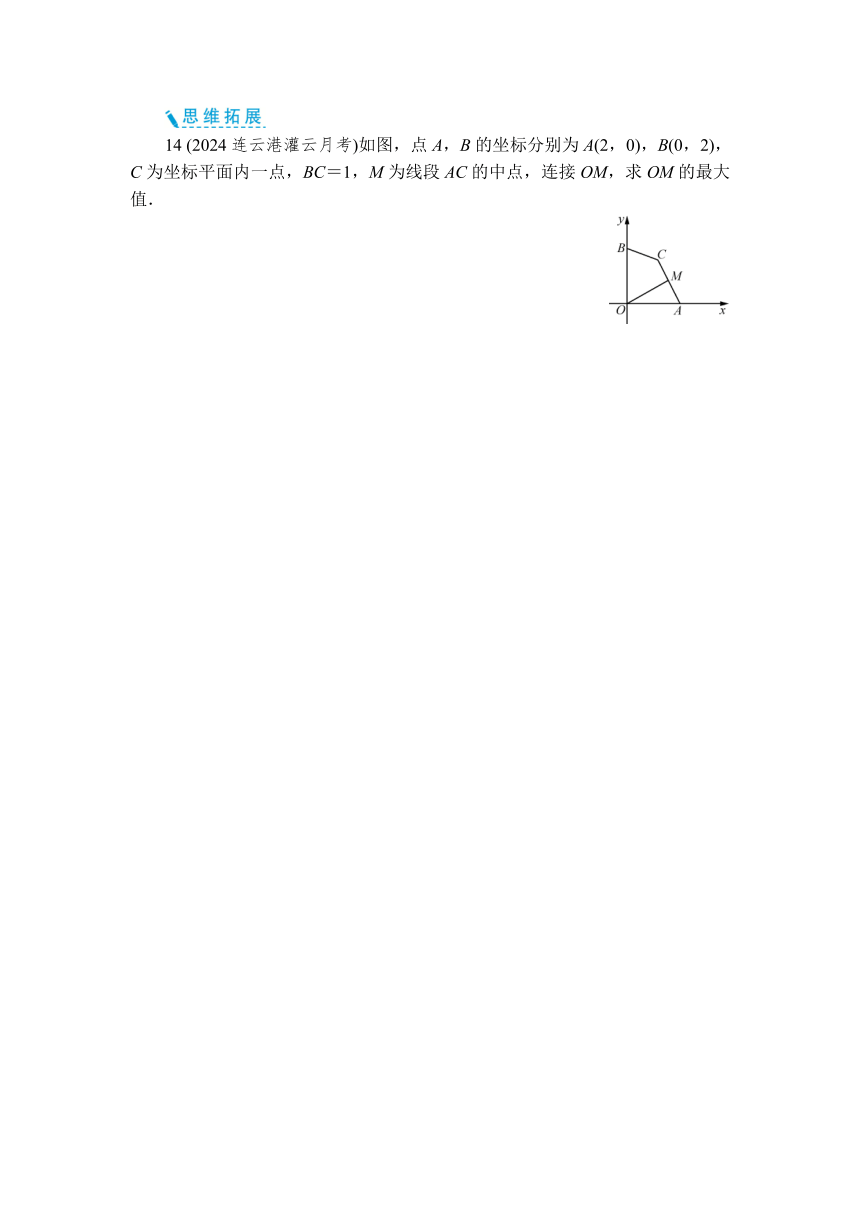
14 (2024连云港灌云月考)如图,点A,B的坐标分别为A(2,0),B(0,2),C为坐标平面内一点,BC=1,M为线段AC的中点,连接OM,求OM的最大值.
第2课时 与圆有关的概念
1. (1) 连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径,圆上任意两点间的部分叫做圆弧;
(2) 圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆.大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧;
(3) 顶点在圆心的角叫做圆心角;圆心相同,半径不相等的两个圆叫做同心圆;能够互相重合的两个圆叫做等圆;能够互相重合的弧叫做等弧.
2. 同圆或等圆的半径相等.
建议用时:20分钟
1 (2024无锡梁溪期中)下列说法中,正确的是( )
A. 弦是直径 B. 弧是半圆
C. 半圆是圆中最长的弧 D. 直径是圆中最长的弦
2 如图,在⊙O中,点A,O,D以及点E,D,C分别在同一直线上,则图中弦的条数为( )
A. 2 B. 3 C. 4 D. 5
(第2题) (第3题) (第4题) (第6题)
3 如图,图中的直径是________,非直径的弦有________;图中以A为端点的弧中,优弧有________,劣弧有________.
4 (2024南京栖霞月考)如图,AB是⊙O的直径,∠C=20°,则∠BOC的度数是________.
5 在平面直角坐标系xOy中,以点(4,0)为圆心,5为半径画圆,则圆与y轴的交点坐标为________.
6 如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,且CD=4,BD=2,则直径AB的长为________.
7 如图,BD=OD,∠B=38°,求∠AOD的度数.
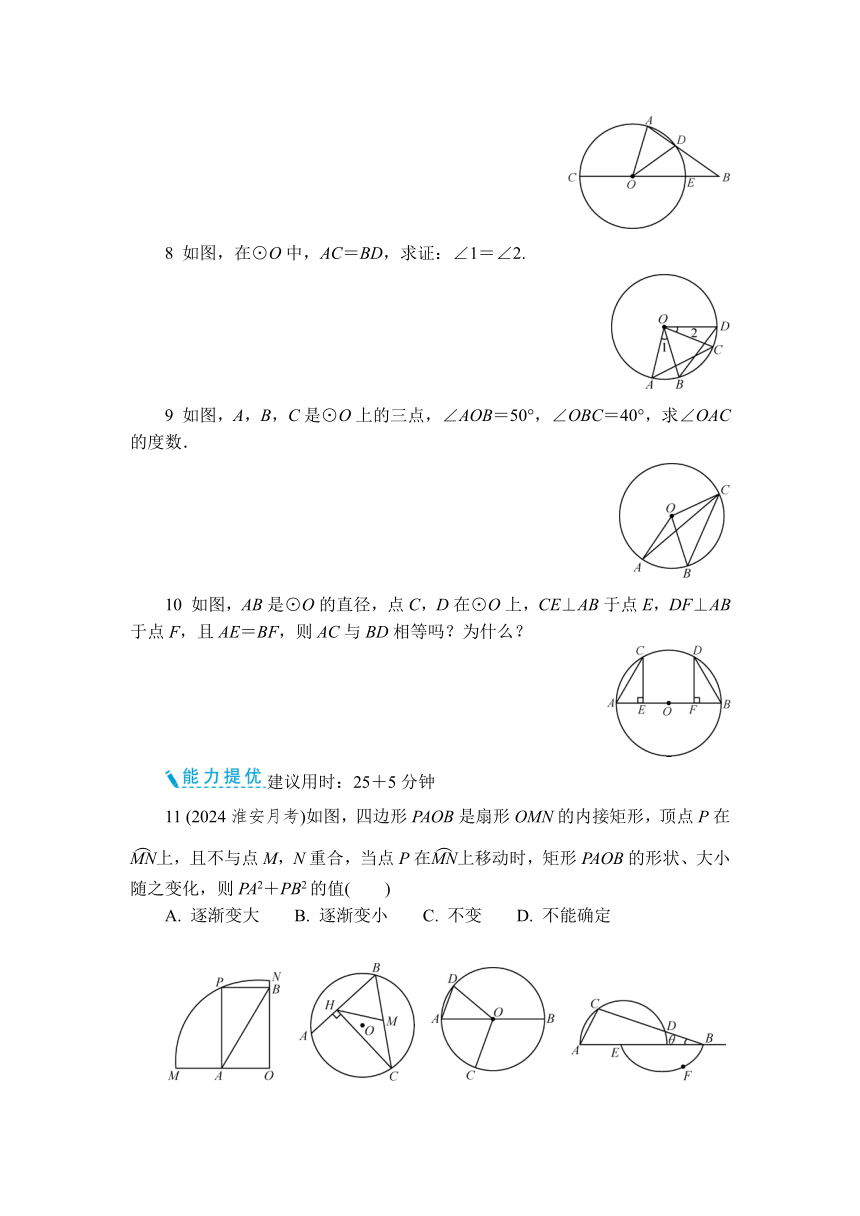
8 如图,在⊙O中,AC=BD,求证:∠1=∠2.
9 如图,A,B,C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
10 如图,AB是⊙O的直径,点C,D在⊙O上,CE⊥AB于点E,DF⊥AB于点F,且AE=BF,则AC与BD相等吗?为什么?
建议用时:25+5分钟
11 (2024淮安月考)如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与点M,N重合,当点P在上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
A. 逐渐变大 B. 逐渐变小 C. 不变 D. 不能确定
(第11题) (第12题) (第13题) (第14题)
12 (2024南京栖霞月考)如图,AB是⊙O的弦,C是优弧AB上的动点(点C不与点A,B重合),CH⊥AB,垂足为H,M是BC的中点.若⊙O的半径是3,则MH长的最大值是( )
A. 3 B. 4 C. 5 D. 6
13 (2024苏州常熟期中)如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD=________.
14 如图,过A,C,D三点的圆的圆心为点E,过B,F,E三点的圆的圆心为点D,如果∠A=72°,那么∠θ=________.
15 如图,在△ABC中,以点A为圆心画弧分别交BA的延长线,AC于点E,F,连接EF并延长交BC于点G,EG⊥BC.求证:AB=AC.
16 如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于点D,AD<BD,若CD=2 cm,AB=5 cm,求AD,AC的长.
17 如图,在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM,OP上,且∠POM=45°,求正方形ABCD的边长.
18 在⊙O中,直径AB=10,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1) 如图1,当PQ∥AB时,求PQ的长度;
(2) 如图2,当点P在BC上移动时,求PQ长度的最大值.
图1 图2
2.1 圆
第1课时 圆 的 概 念
1. B 2. B 3. A 4. 圆心 半径 5. 点P在圆外 6. 以点O为圆心,半径为7 cm的圆 7. 点P在⊙O内
8. 略 9. A 10. 2或3 11. 3或4 12. 6<r<10
13. 证明:如图,连接AC,交BD于点O,连接EO,FO.
因为四边形ABCD是平行四边形,所以O为AC的中点,所以AO=CO=AC.
因为AE⊥BC,AF⊥CD,所以∠AEC=∠AFC=90°,
所以EO=AC,FO=AC,所以AO=CO=EO=FO,
所以A,E,C,F四点在以点O为圆心,AC长为半径的圆上.
14. 解:如图,因为C为坐标平面内一点,BC=1,
所以点C在⊙B上,且半径为1.
在x轴负半轴上取一点D,令OD=OA=2,连接CD,
因为AM=CM,OD=OA,
所以OM是△ACD的中位线,
所以OM=CD,
故当OM最大时,CD最大,而当D,B,C三点共线,点C在DB的延长线上时,CD最大.
因为OB=OD=2,∠BOD=90°,
所以BD=2,
所以CD=2+1,
所以OM=CD=+,即OM的最大值为+.
第2课时 与圆有关的概念
1. D 2. B 3. AB CD,EF ,,, ,,, 4. 40° 5. (0,3),(0,-3) 6. 10
7. 解:因为BD=OD,∠B=38°,
所以∠DOB=∠B=38°,
所以∠ADO=∠DOB+∠B=2×38°=76°.
因为OA=OD,
所以∠A=∠ADO=76°,
所以∠AOD=180°-∠A-∠ADO=180°-76°-76°=28°.
8. 证明:因为在⊙O中,AC=BD,OA=OB=OC=OD,
所以△OAC≌△OBD(SSS),
所以∠AOC=∠BOD,
所以∠1+∠BOC=∠2+∠BOC,
所以∠1=∠2.
9. 解:因为OB=OC,所以∠OCB=∠OBC=40°,
所以∠BOC=180°-∠OBC-∠OCB=100°,
所以∠AOC=∠AOB+∠BOC=150°.
因为OA=OC,所以∠OAC==15°.
10. 解:AC与BD相等.理由如下:
如图,连接OC,OD.
因为OA=OB,AE=BF,
所以OE=OF.
因为CE⊥AB,DF⊥AB,
所以∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
所以Rt△OEC≌Rt△OFD(HL),
所以∠COE=∠DOF.
在△OAC和△OBD中,
所以△OAC≌△OBD,
所以AC=BD.
11. C 12. A 13. 40° 14. 12°
15. 证明:因为AE=AF,
所以∠AEF=∠AFE.
因为∠AFE=∠CFG,
所以∠AEF=∠CFG.
因为EG⊥BC,
所以∠AEF+∠B=90°,∠C+∠CFG=90°,
所以∠B=∠C,
所以AB=AC.
16. 解:如图,连接OC.
因为AB=5 cm,
所以OC=OA=AB= cm,
在Rt△CDO中,由勾股定理,得DO==(cm),
所以AD=AO-DO=-=1(cm),
在Rt△ADC中,由勾股定理,得AC==(cm),
故AD的长为1 cm,AC的长为 cm.
17. 解:连接AO.
因为四边形ABCD是正方形,
所以∠ABC=∠BCD=90°,AB=BC=CD,
所以∠DCO=90°.
因为∠POM=45°,所以∠CDO=45°,
所以CD=CO,
所以BO=BC+CO=BC+CD,所以BO=2AB.
因为MN=10,所以AO=5.
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,解得AB=,
所以正方形ABCD的边长为 .
18. 解:(1) 如图1,连接OQ.
因为PQ∥AB,OP⊥PQ,
所以OP⊥AB.
在Rt△OBP中,因为∠ABC=30°,所以BP=2OP,
所以OP2+OB2=BP2=4OP2.又OB=5,
所以OP=.
在Rt△OPQ中,因为OP=,OQ=5,
所以PQ==.
(2) 如图2,连接OQ.
当OP的长最小时,PQ的长最大,此时OP⊥BC,
则OP=OB=,
所以PQ===,
所以PQ长度的最大值为.
图1 图2
第1课时 圆 的 概 念
1. (1) 圆是到定点的距离等于定长的点的集合,定点就是圆心,定长就是半径;
(2) 圆上各点到圆心的距离都等于半径;到圆心的距离等于半径的点都在圆上.
2. 已知⊙O的半径为r,点P到圆心O的距离为d,则
(1) 点P在⊙O上 d=r;(2) 点P在⊙O外 d>r;(3) 点P在⊙O内 d
1 (2024南京鼓楼月考)在△ABC中,AB=AC,若以点A为圆心,以AB为半径作圆,则点C与⊙A的位置关系为( )
A. 点C在⊙A内 B. 点C在⊙A上
C. 点C在⊙A外 D. 点C在⊙A内或⊙A外
2 (2024南京江宁月考)若⊙O的半径为3 cm,点A不在⊙O内,则OA的长( )
A. 大于3 cm B. 不小于3 cm C. 大于6 cm D. 不小于6 cm
3 在平面直角坐标系中,圆心O为坐标原点,⊙O的半径为5,则点P(3,4)与⊙O的位置关系为( )
A. 点P在⊙O上 B. 点P在⊙O外
C. 点P在⊙O内 D. 无法确定
4 早在2 000多年前的战国时期,《墨经》一书中就给出了圆的描述性定义:“圜(这里读yuan),一中同长也”这就是说,圆是平面内到定点的距离等于定长的点的集合.其中,定点是________,定长是________.
5 (2024无锡江阴月考)若⊙O的半径为4 cm,点P到圆心O的距离为5 cm,则点P与⊙O的位置关系是________.
6 (2024盐城射阳月考)到点O的距离等于7 cm的点的集合是________.
7 (2024扬州江都月考)已知⊙O的半径是8,点P到圆心O的距离d为方程x2-4x-5=0的一个根,则点P与⊙O的位置关系是________.
8 作线段AB=3 cm,按下列要求作图:
(1) 到点A的距离等于2 cm的点的集合;
(2) 到点B的距离等于1.5 cm的点的集合;
(3) 到点A的距离大于2 cm且到点B的距离小于1.5 cm的点的集合.(用阴影部分表示)
建议用时:25+5分钟
9 如图,在Rt△ABC中,∠C=90°,AC=8,BC=14,点D在边BC上,CD=6,以点D为圆心作⊙D,其半径长为r,要使点A恰在⊙D外,点B在⊙D内,则r的取值范围是( )
A. 8<r<10 B. 6<r<8 C. 6<r<10 D. 2<r<14
(第9题) (第11题) (第12题)
10 (2024常州武进月考)已知P为平面内一点,若点P到⊙O上的点的最长距离为5,最短距离为1,则⊙O的半径为__________.
11 (2024无锡江阴月考)如图,原点右边7个单位长度处有一点P,数轴上半径为1的⊙O从原点O开始以每秒2个单位长度的速度向右运动,经过________s,点P在⊙O上.
12 (2024连云港连云月考)如图,在矩形ABCD中,AB=8,AD=6,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是________.
13 如图,在平行四边形ABCD中,∠BAD为钝角,且AE⊥BC于点E,AF⊥CD于点F,连接BD.求证:A,E,C,F四点在同一个圆上.
14 (2024连云港灌云月考)如图,点A,B的坐标分别为A(2,0),B(0,2),C为坐标平面内一点,BC=1,M为线段AC的中点,连接OM,求OM的最大值.
第2课时 与圆有关的概念
1. (1) 连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径,圆上任意两点间的部分叫做圆弧;
(2) 圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆.大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧;
(3) 顶点在圆心的角叫做圆心角;圆心相同,半径不相等的两个圆叫做同心圆;能够互相重合的两个圆叫做等圆;能够互相重合的弧叫做等弧.
2. 同圆或等圆的半径相等.
建议用时:20分钟
1 (2024无锡梁溪期中)下列说法中,正确的是( )
A. 弦是直径 B. 弧是半圆
C. 半圆是圆中最长的弧 D. 直径是圆中最长的弦
2 如图,在⊙O中,点A,O,D以及点E,D,C分别在同一直线上,则图中弦的条数为( )
A. 2 B. 3 C. 4 D. 5
(第2题) (第3题) (第4题) (第6题)
3 如图,图中的直径是________,非直径的弦有________;图中以A为端点的弧中,优弧有________,劣弧有________.
4 (2024南京栖霞月考)如图,AB是⊙O的直径,∠C=20°,则∠BOC的度数是________.
5 在平面直角坐标系xOy中,以点(4,0)为圆心,5为半径画圆,则圆与y轴的交点坐标为________.
6 如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,且CD=4,BD=2,则直径AB的长为________.
7 如图,BD=OD,∠B=38°,求∠AOD的度数.
8 如图,在⊙O中,AC=BD,求证:∠1=∠2.
9 如图,A,B,C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
10 如图,AB是⊙O的直径,点C,D在⊙O上,CE⊥AB于点E,DF⊥AB于点F,且AE=BF,则AC与BD相等吗?为什么?
建议用时:25+5分钟
11 (2024淮安月考)如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与点M,N重合,当点P在上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
A. 逐渐变大 B. 逐渐变小 C. 不变 D. 不能确定
(第11题) (第12题) (第13题) (第14题)
12 (2024南京栖霞月考)如图,AB是⊙O的弦,C是优弧AB上的动点(点C不与点A,B重合),CH⊥AB,垂足为H,M是BC的中点.若⊙O的半径是3,则MH长的最大值是( )
A. 3 B. 4 C. 5 D. 6
13 (2024苏州常熟期中)如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD=________.
14 如图,过A,C,D三点的圆的圆心为点E,过B,F,E三点的圆的圆心为点D,如果∠A=72°,那么∠θ=________.
15 如图,在△ABC中,以点A为圆心画弧分别交BA的延长线,AC于点E,F,连接EF并延长交BC于点G,EG⊥BC.求证:AB=AC.
16 如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于点D,AD<BD,若CD=2 cm,AB=5 cm,求AD,AC的长.
17 如图,在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM,OP上,且∠POM=45°,求正方形ABCD的边长.
18 在⊙O中,直径AB=10,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1) 如图1,当PQ∥AB时,求PQ的长度;
(2) 如图2,当点P在BC上移动时,求PQ长度的最大值.
图1 图2
2.1 圆
第1课时 圆 的 概 念
1. B 2. B 3. A 4. 圆心 半径 5. 点P在圆外 6. 以点O为圆心,半径为7 cm的圆 7. 点P在⊙O内
8. 略 9. A 10. 2或3 11. 3或4 12. 6<r<10
13. 证明:如图,连接AC,交BD于点O,连接EO,FO.
因为四边形ABCD是平行四边形,所以O为AC的中点,所以AO=CO=AC.
因为AE⊥BC,AF⊥CD,所以∠AEC=∠AFC=90°,
所以EO=AC,FO=AC,所以AO=CO=EO=FO,
所以A,E,C,F四点在以点O为圆心,AC长为半径的圆上.
14. 解:如图,因为C为坐标平面内一点,BC=1,
所以点C在⊙B上,且半径为1.
在x轴负半轴上取一点D,令OD=OA=2,连接CD,
因为AM=CM,OD=OA,
所以OM是△ACD的中位线,
所以OM=CD,
故当OM最大时,CD最大,而当D,B,C三点共线,点C在DB的延长线上时,CD最大.
因为OB=OD=2,∠BOD=90°,
所以BD=2,
所以CD=2+1,
所以OM=CD=+,即OM的最大值为+.
第2课时 与圆有关的概念
1. D 2. B 3. AB CD,EF ,,, ,,, 4. 40° 5. (0,3),(0,-3) 6. 10
7. 解:因为BD=OD,∠B=38°,
所以∠DOB=∠B=38°,
所以∠ADO=∠DOB+∠B=2×38°=76°.
因为OA=OD,
所以∠A=∠ADO=76°,
所以∠AOD=180°-∠A-∠ADO=180°-76°-76°=28°.
8. 证明:因为在⊙O中,AC=BD,OA=OB=OC=OD,
所以△OAC≌△OBD(SSS),
所以∠AOC=∠BOD,
所以∠1+∠BOC=∠2+∠BOC,
所以∠1=∠2.
9. 解:因为OB=OC,所以∠OCB=∠OBC=40°,
所以∠BOC=180°-∠OBC-∠OCB=100°,
所以∠AOC=∠AOB+∠BOC=150°.
因为OA=OC,所以∠OAC==15°.
10. 解:AC与BD相等.理由如下:
如图,连接OC,OD.
因为OA=OB,AE=BF,
所以OE=OF.
因为CE⊥AB,DF⊥AB,
所以∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
所以Rt△OEC≌Rt△OFD(HL),
所以∠COE=∠DOF.
在△OAC和△OBD中,
所以△OAC≌△OBD,
所以AC=BD.
11. C 12. A 13. 40° 14. 12°
15. 证明:因为AE=AF,
所以∠AEF=∠AFE.
因为∠AFE=∠CFG,
所以∠AEF=∠CFG.
因为EG⊥BC,
所以∠AEF+∠B=90°,∠C+∠CFG=90°,
所以∠B=∠C,
所以AB=AC.
16. 解:如图,连接OC.
因为AB=5 cm,
所以OC=OA=AB= cm,
在Rt△CDO中,由勾股定理,得DO==(cm),
所以AD=AO-DO=-=1(cm),
在Rt△ADC中,由勾股定理,得AC==(cm),
故AD的长为1 cm,AC的长为 cm.
17. 解:连接AO.
因为四边形ABCD是正方形,
所以∠ABC=∠BCD=90°,AB=BC=CD,
所以∠DCO=90°.
因为∠POM=45°,所以∠CDO=45°,
所以CD=CO,
所以BO=BC+CO=BC+CD,所以BO=2AB.
因为MN=10,所以AO=5.
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,解得AB=,
所以正方形ABCD的边长为 .
18. 解:(1) 如图1,连接OQ.
因为PQ∥AB,OP⊥PQ,
所以OP⊥AB.
在Rt△OBP中,因为∠ABC=30°,所以BP=2OP,
所以OP2+OB2=BP2=4OP2.又OB=5,
所以OP=.
在Rt△OPQ中,因为OP=,OQ=5,
所以PQ==.
(2) 如图2,连接OQ.
当OP的长最小时,PQ的长最大,此时OP⊥BC,
则OP=OB=,
所以PQ===,
所以PQ长度的最大值为.
图1 图2
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
