2.1~2.4 阶 段 提 优 同步练(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 2.1~2.4 阶 段 提 优 同步练(含答案) 2025-2026学年数学苏科版九年级上册 | 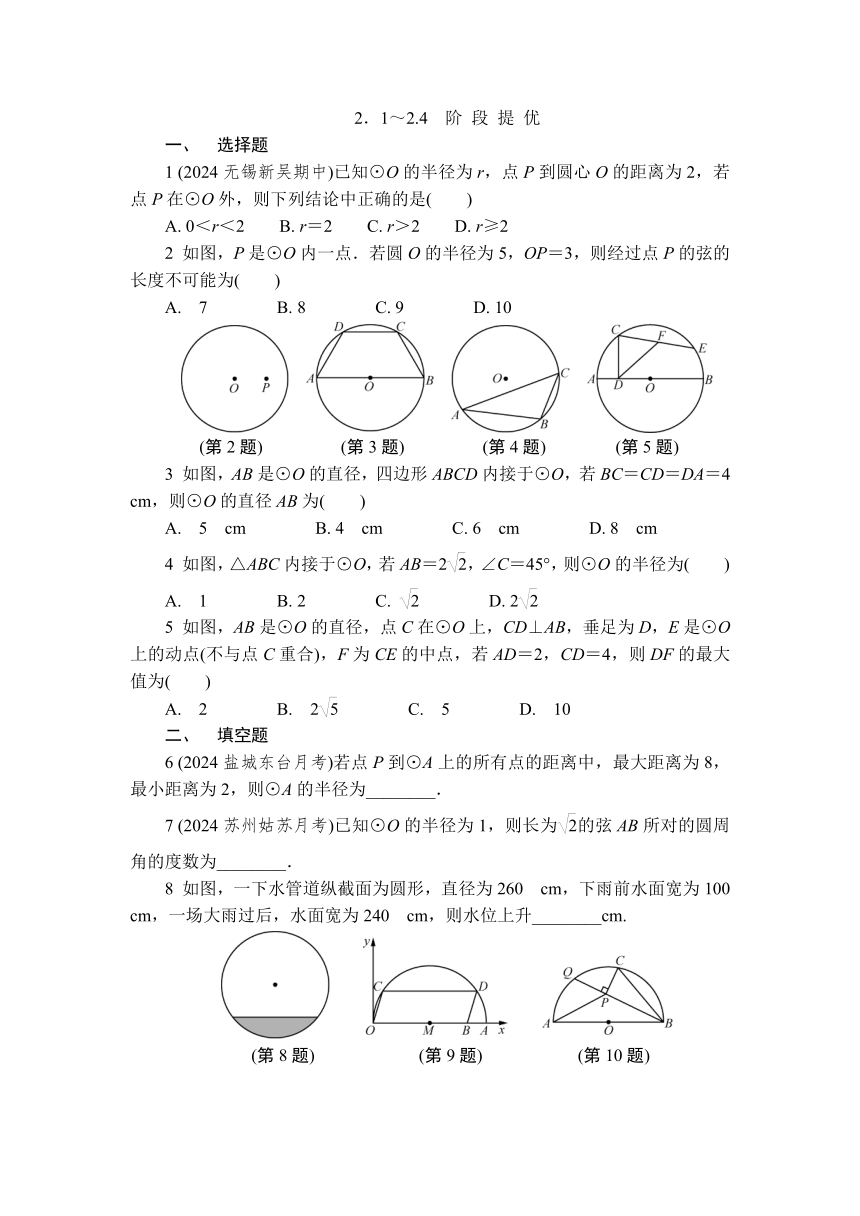 | |
| 格式 | docx | ||
| 文件大小 | 207.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 23:08:16 | ||
图片预览


文档简介
2.1~2.4 阶 段 提 优
一、 选择题
1 (2024无锡新吴期中)已知⊙O的半径为r,点P到圆心O的距离为2,若点P在⊙O外,则下列结论中正确的是( )
A. 0<r<2 B. r=2 C. r>2 D. r≥2
2 如图,P是⊙O内一点.若圆O的半径为5,OP=3,则经过点P的弦的长度不可能为( )
A. 7 B. 8 C. 9 D. 10
(第2题) (第3题) (第4题) (第5题)
3 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4 cm,则⊙O的直径AB为( )
A. 5 cm B. 4 cm C. 6 cm D. 8 cm
4 如图,△ABC内接于⊙O,若AB=2,∠C=45°,则⊙O的半径为( )
A. 1 B. 2 C. D. 2
5 如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,E是⊙O上的动点(不与点C重合),F为CE的中点,若AD=2,CD=4,则DF的最大值为( )
A. 2 B. 2 C. 5 D. 10
二、 填空题
6 (2024盐城东台月考)若点P到⊙A上的所有点的距离中,最大距离为8,最小距离为2,则⊙A的半径为________.
7 (2024苏州姑苏月考)已知⊙O的半径为1,则长为的弦AB所对的圆周角的度数为________.
8 如图,一下水管道纵截面为圆形,直径为260 cm,下雨前水面宽为100 cm,一场大雨过后,水面宽为240 cm,则水位上升________cm.
(第8题) (第9题) (第10题)
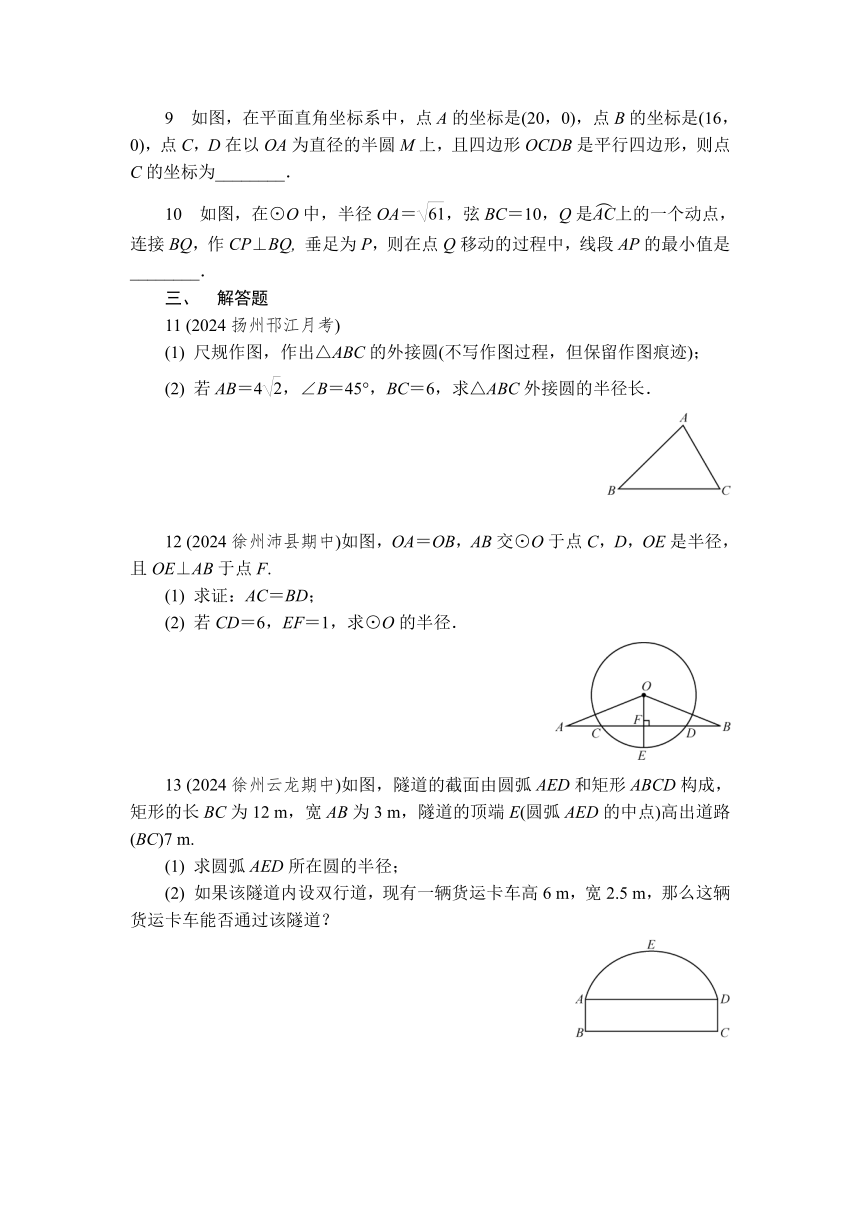
9 如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为________.
10 如图,在⊙O中,半径OA=,弦BC=10,Q是上的一个动点,连接BQ,作CP⊥BQ, 垂足为P,则在点Q移动的过程中,线段AP的最小值是________.
三、 解答题
11 (2024扬州邗江月考)
(1) 尺规作图,作出△ABC的外接圆(不写作图过程,但保留作图痕迹);
(2) 若AB=4,∠B=45°,BC=6,求△ABC外接圆的半径长.
12 (2024徐州沛县期中)如图,OA=OB,AB交⊙O于点C,D,OE是半径,且OE⊥AB于点F.
(1) 求证:AC=BD;
(2) 若CD=6,EF=1,求⊙O的半径.
13 (2024徐州云龙期中)如图,隧道的截面由圆弧AED和矩形ABCD构成,矩形的长BC为12 m,宽AB为3 m,隧道的顶端E(圆弧AED的中点)高出道路(BC)7 m.
(1) 求圆弧AED所在圆的半径;
(2) 如果该隧道内设双行道,现有一辆货运卡车高6 m,宽2.5 m,那么这辆货运卡车能否通过该隧道?
14 (2024浙江)如图,在圆内接四边形ABCD中,AD<AC,∠ADC<∠BAD,延长AD至点E,使AE=AC,延长BA至点F,连接EF,使∠AFE=∠ADC.
(1) 若∠AFE=60°,CD为直径,求∠ABD的度数;
(2) 求证:①EF∥BC;
②EF=BD.
2.1~2.4 阶 段 提 优
1. A 2. A 3. D 4. B 5. C
6. 5或3 7. 45°或135° 8. 70或170 9. (2,6) 10. 8
11. 解:(1) 尺规作图,如图1.
(2) 如图2,连接OB.
因为DH,OE分别垂直平分AB,BC,AB=4,BC=6,
所以BD=2,BE=3.
又因为∠ABC=45°,∠BDO=90°,
所以BH=4,∠EHO=45°,
所以OE=EH=BH-BE=4-3=1,
所以BO==,
所以△ABC外接圆的半径长为.
图1 图2
12. (1) 证明:因为OE⊥AB,CD为⊙O的弦,
所以CF=DF.
因为OA=OB,OE⊥AB,
所以AF=BF,
所以AF-CF=BF-DF,
所以AC=BD.
(2) 解:如图,连接OC.
因为OE⊥AB,CD为⊙O的弦,
所以CF=CD=3,∠OFC=90°,
所以CO2=CF2+OF2.
设⊙O的半径为r,
则r2=32+(r-1)2,
解得r=5,
所以⊙O的半径是5.
13. 解:(1) 设圆心为点O,半径为R,如图,连接OA,OE,设OE与AD交于点F.
因为隧道的顶端E是圆弧AED的中点,高出道路(BC)7 m,
所以AD⊥OE,AF=DF=AD.
因为矩形的长BC为12 m,宽AB为3 m,
所以AD∥BC,且AD,BC之间的距离为3 m,AD=BC=12 m,
所以EF=7-3=4(m),AF=DF=6 m,
所以OF=(R-4)m,
所以R2=(R-4)2+62,
解得R=6.5 m,
故圆弧AED所在圆的半径为6.5 m.
(2) 如图,在圆弧AED上取一点H,过点H作HG⊥OE于点G,且使得HG=2.5,
所以OG===6(m).
因为点O到BC的距离为7-6.5=0.5(m),
所以点G到BC的距离为6+0.5=6.5(m)>6m,
故这辆货运卡车能通过该隧道.
14. (1) 解:因为CD为直径,
所以∠CAD=90°.
因为∠AFE=∠ADC=60°,
所以∠ACD=90°-60°=30°,
所以∠ABD=∠ACD=30°.
(2) 证明:①如图,延长AB至点M.
因为四边形ABCD是圆内接四边形,
所以∠CBM=∠ADC.
又因为∠AFE=∠ADC,
所以∠AFE=∠CBM,
所以EF∥BC.
②过点D作DG∥BC交⊙O于点G,连接AG,CG.
因为DG∥BC,所以=,
所以BD=CG.
因为四边形ACGD是圆内接四边形,
所以∠GDE=∠ACG.
因为EF∥DG,
所以∠DEF=∠GDE,
所以∠DEF=∠ACG.
因为∠AFE=∠ADC,∠ADC=∠AGC,
所以∠AFE=∠AGC.
因为AE=AC,
所以△AEF≌△ACG(AAS),
所以EF=CG,
所以EF=BD.
一、 选择题
1 (2024无锡新吴期中)已知⊙O的半径为r,点P到圆心O的距离为2,若点P在⊙O外,则下列结论中正确的是( )
A. 0<r<2 B. r=2 C. r>2 D. r≥2
2 如图,P是⊙O内一点.若圆O的半径为5,OP=3,则经过点P的弦的长度不可能为( )
A. 7 B. 8 C. 9 D. 10
(第2题) (第3题) (第4题) (第5题)
3 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4 cm,则⊙O的直径AB为( )
A. 5 cm B. 4 cm C. 6 cm D. 8 cm
4 如图,△ABC内接于⊙O,若AB=2,∠C=45°,则⊙O的半径为( )
A. 1 B. 2 C. D. 2
5 如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,E是⊙O上的动点(不与点C重合),F为CE的中点,若AD=2,CD=4,则DF的最大值为( )
A. 2 B. 2 C. 5 D. 10
二、 填空题
6 (2024盐城东台月考)若点P到⊙A上的所有点的距离中,最大距离为8,最小距离为2,则⊙A的半径为________.
7 (2024苏州姑苏月考)已知⊙O的半径为1,则长为的弦AB所对的圆周角的度数为________.
8 如图,一下水管道纵截面为圆形,直径为260 cm,下雨前水面宽为100 cm,一场大雨过后,水面宽为240 cm,则水位上升________cm.
(第8题) (第9题) (第10题)
9 如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为________.
10 如图,在⊙O中,半径OA=,弦BC=10,Q是上的一个动点,连接BQ,作CP⊥BQ, 垂足为P,则在点Q移动的过程中,线段AP的最小值是________.
三、 解答题
11 (2024扬州邗江月考)
(1) 尺规作图,作出△ABC的外接圆(不写作图过程,但保留作图痕迹);
(2) 若AB=4,∠B=45°,BC=6,求△ABC外接圆的半径长.
12 (2024徐州沛县期中)如图,OA=OB,AB交⊙O于点C,D,OE是半径,且OE⊥AB于点F.
(1) 求证:AC=BD;
(2) 若CD=6,EF=1,求⊙O的半径.
13 (2024徐州云龙期中)如图,隧道的截面由圆弧AED和矩形ABCD构成,矩形的长BC为12 m,宽AB为3 m,隧道的顶端E(圆弧AED的中点)高出道路(BC)7 m.
(1) 求圆弧AED所在圆的半径;
(2) 如果该隧道内设双行道,现有一辆货运卡车高6 m,宽2.5 m,那么这辆货运卡车能否通过该隧道?
14 (2024浙江)如图,在圆内接四边形ABCD中,AD<AC,∠ADC<∠BAD,延长AD至点E,使AE=AC,延长BA至点F,连接EF,使∠AFE=∠ADC.
(1) 若∠AFE=60°,CD为直径,求∠ABD的度数;
(2) 求证:①EF∥BC;
②EF=BD.
2.1~2.4 阶 段 提 优
1. A 2. A 3. D 4. B 5. C
6. 5或3 7. 45°或135° 8. 70或170 9. (2,6) 10. 8
11. 解:(1) 尺规作图,如图1.
(2) 如图2,连接OB.
因为DH,OE分别垂直平分AB,BC,AB=4,BC=6,
所以BD=2,BE=3.
又因为∠ABC=45°,∠BDO=90°,
所以BH=4,∠EHO=45°,
所以OE=EH=BH-BE=4-3=1,
所以BO==,
所以△ABC外接圆的半径长为.
图1 图2
12. (1) 证明:因为OE⊥AB,CD为⊙O的弦,
所以CF=DF.
因为OA=OB,OE⊥AB,
所以AF=BF,
所以AF-CF=BF-DF,
所以AC=BD.
(2) 解:如图,连接OC.
因为OE⊥AB,CD为⊙O的弦,
所以CF=CD=3,∠OFC=90°,
所以CO2=CF2+OF2.
设⊙O的半径为r,
则r2=32+(r-1)2,
解得r=5,
所以⊙O的半径是5.
13. 解:(1) 设圆心为点O,半径为R,如图,连接OA,OE,设OE与AD交于点F.
因为隧道的顶端E是圆弧AED的中点,高出道路(BC)7 m,
所以AD⊥OE,AF=DF=AD.
因为矩形的长BC为12 m,宽AB为3 m,
所以AD∥BC,且AD,BC之间的距离为3 m,AD=BC=12 m,
所以EF=7-3=4(m),AF=DF=6 m,
所以OF=(R-4)m,
所以R2=(R-4)2+62,
解得R=6.5 m,
故圆弧AED所在圆的半径为6.5 m.
(2) 如图,在圆弧AED上取一点H,过点H作HG⊥OE于点G,且使得HG=2.5,
所以OG===6(m).
因为点O到BC的距离为7-6.5=0.5(m),
所以点G到BC的距离为6+0.5=6.5(m)>6m,
故这辆货运卡车能通过该隧道.
14. (1) 解:因为CD为直径,
所以∠CAD=90°.
因为∠AFE=∠ADC=60°,
所以∠ACD=90°-60°=30°,
所以∠ABD=∠ACD=30°.
(2) 证明:①如图,延长AB至点M.
因为四边形ABCD是圆内接四边形,
所以∠CBM=∠ADC.
又因为∠AFE=∠ADC,
所以∠AFE=∠CBM,
所以EF∥BC.
②过点D作DG∥BC交⊙O于点G,连接AG,CG.
因为DG∥BC,所以=,
所以BD=CG.
因为四边形ACGD是圆内接四边形,
所以∠GDE=∠ACG.
因为EF∥DG,
所以∠DEF=∠GDE,
所以∠DEF=∠ACG.
因为∠AFE=∠ADC,∠ADC=∠AGC,
所以∠AFE=∠AGC.
因为AE=AC,
所以△AEF≌△ACG(AAS),
所以EF=CG,
所以EF=BD.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
