2.2 圆的对称性 同步练 (含答案) 2025-2026学年数学苏科版(2024)九年级上册
文档属性
| 名称 | 2.2 圆的对称性 同步练 (含答案) 2025-2026学年数学苏科版(2024)九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 409.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 00:00:00 | ||
图片预览



文档简介
2.2 圆的对称性
第1课时 圆心角、弧、弦之间的关系
1. 圆是中心对称图形,圆心是它的对称中心.
2. 圆心角、弧、弦之间的关系:
(1) 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;
(2) 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
3. 圆心角的度数与它所对的弧的度数相等.
建议用时:20分钟
1 下列说法中,正确的是( )
A. 等弦所对的弧相等 B. 等弧所对的弦相等
C. 圆心角相等,所对的弦相等 D. 相等的弦所对的圆心角相等
2 (2024苏州高新区月考)如图,A,B,C,D都是⊙O上的点,若CD=BD,∠AOC=108°,则∠AOD等于( )
A. 140° B. 144° C. 146° D. 150°
(第2题) (第3题) (第5题)
3 (2024南京期中)如图,点A,B,C,D都在⊙O上,OB⊥AC,BC=CD,则下列说法中错误的是( )
A. = B. ∠AOC=∠BOD C. AC=2CD D. OC⊥BD
4 已知⊙O的半径为12 cm,弦AB将圆分成的两段弧所对的圆心角度数之比为1∶5,则∠AOB的度数为________,弦AB的长为________cm.
5 如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为________,的度数为________.
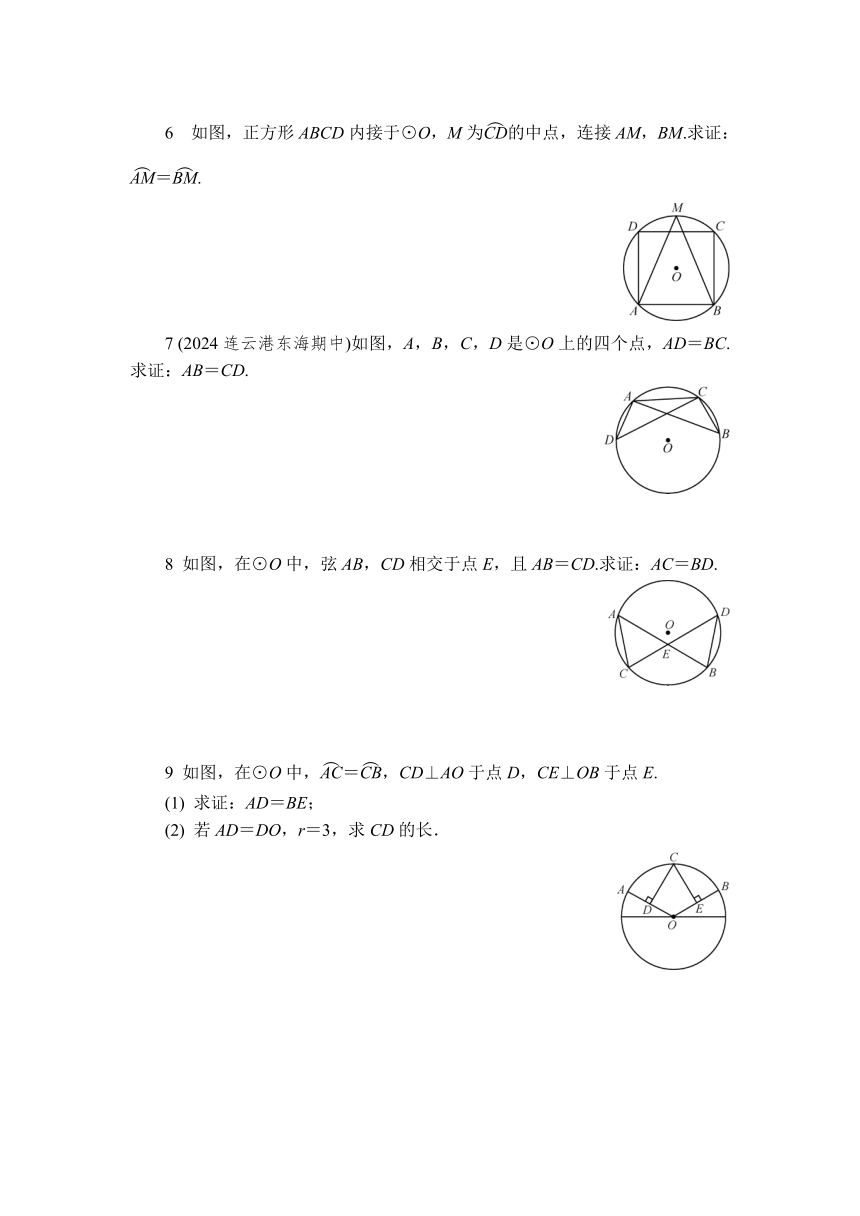
6 如图,正方形ABCD内接于⊙O,M为的中点,连接AM,BM.求证:=.
7 (2024连云港东海期中)如图,A,B,C,D是⊙O上的四个点,AD=BC.求证:AB=CD.
8 如图,在⊙O中,弦AB,CD相交于点E,且AB=CD.求证:AC=BD.
9 如图,在⊙O中,=,CD⊥AO于点D,CE⊥OB于点E.
(1) 求证:AD=BE;
(2) 若AD=DO,r=3,求CD的长.
10 如图,AC,BD是⊙O的弦,分别连接OA,OB,OC,OD,∠AOB=∠COD,AC与OB交于点E,⊙O的半径为6.
(1) 求证:=;
(2) 若BD=10,E为AC的中点,求OE的长.
建议用时:25+5分钟
11 (2024扬州宝应期中)如图,在⊙O中,点A,B,C在圆上,且弧AB的长等于弧AC长的2倍,则下列结论中正确的是( )
A. AB=2AC B. AB>2AC
C. AB<2AC D. 以上结论都不对
(第11题) (第12题) (第13题) (第14题)
12 如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为( )
A. 30° B. 40° C. 50° D. 60°
13 如图,已知C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是________.
14 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则的度数为________.
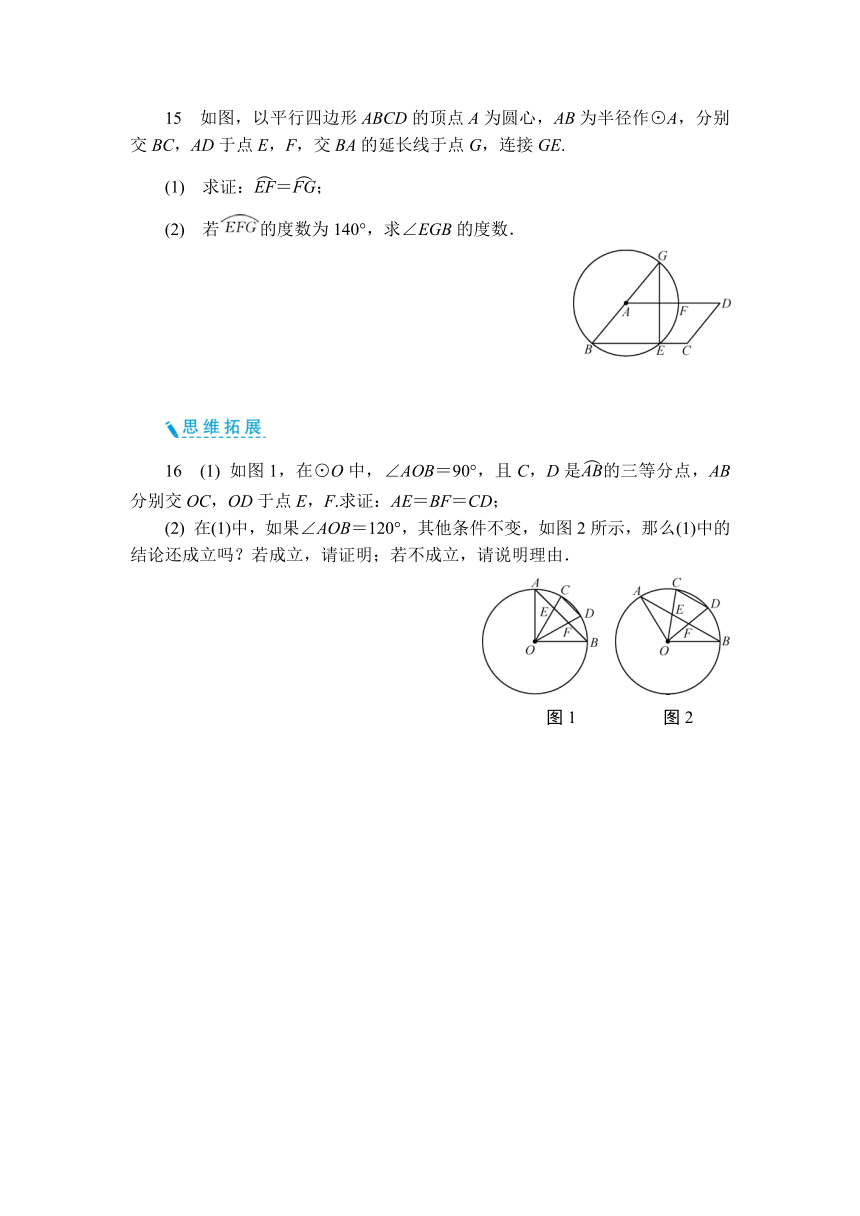
15 如图,以平行四边形ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于点E,F,交BA的延长线于点G,连接GE.
(1) 求证:=;
(2) 若的度数为140°,求∠EGB的度数.
16 (1) 如图1,在⊙O中,∠AOB=90°,且C,D是的三等分点,AB分别交OC,OD于点E,F.求证:AE=BF=CD;
(2) 在(1)中,如果∠AOB=120°,其他条件不变,如图2所示,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
图1 图2
第2课时 垂径定理及推论
1. 圆是轴对称图形,经过圆心的任意一条直线都是它的对称轴.
2. 垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧.
建议用时:20分钟
1 (2024长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为( )
A. 4 B. 4 C. 5 D. 5
(第1题) (第2题) (第3题) (第4题) (第5题)
2 如图,CD是⊙O的弦,AB是⊙O的直径,AB⊥CD,垂足为E,则下列结论中不一定成立的是( )
A. = B. = C. EO=EB D. EC=ED
3 (2024南京江宁月考)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5,CD=6,则AE=________.
4 如图,A,B,C是⊙O上的点,OC⊥AB于点D,且D为OC的中点,若OA=7,则BC的长为________.
5 如图,⊙O是一个盛有水的容器的纵截面,⊙O的半径为10 cm,水的最深处到水面AB的距离为4 cm,则水面AB的宽度为________ cm.
6 如图,A,B是⊙O上的两点,弦AB=a,P是⊙O上不与点A,B重合的一个动点,连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.(用含a的代数式表示)
7 (2024沛县期中)如图,OA=OB,AB交⊙O于点C,D,OE是半径,且OE⊥AB于点F.
(1) 求证:AC=BD;
(2) 若CD=6,EF=1,求⊙O的半径.
建议用时:25+5分钟
8 (2024通辽)如图,圆形拱门的最下端AB在地面上,D为AB的中点,C为拱门的最高点,线段CD经过拱门所在圆的圆心,若AB=1 m,CD=2.5 m,则拱门所在圆的半径为( )
A. 1.25 m B. 1.3 m C. 1.4 m D. 1.45 m
(第8题) (第11题) (第12题)
9 已知⊙O的半径为5,两条弦AB与CD平行,AB=6,CD=8,则AB与CD间的距离为________.
10 已知⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AC的长为________.
11 如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A,B,C,D四点.已知A(6,0),B(-2,0),C(0,3),则点D的坐标为________.
12 如图,在⊙O中,弦AB=6,点C在AB上移动,连接OC,过点C作DE⊥OC交⊙O于点D,E,则DE的最大值为________.
13 如图,在⊙O中,=2,AD⊥OC于点D.求证:AB=2AD.
14 如图,有一座拱桥的形状是圆弧形,它的跨度AB=60 m,拱高PD=18 m.
(1) 求圆弧所在圆的半径r的长;
(2) 当洪水泛滥到跨度只有30 m时,要采取紧急措施.若拱顶离水面只有4 m,即PE=4 m时,是否要采取紧急措施?
2.2 圆的对称性
第1课时 圆心角、弧、弦之间的关系
1. B 2. B 3. C 4. 60° 12 5. 52° 38°
6. 证明:因为四边形ABCD是正方形,
所以AD=BC,所以=.
因为M为的中点,所以=,
所以+=+,所以=.
7. 证明:因为AD=BC,
所以=,
所以+=+,
即=,
所以AB=CD.
8. 证明:因为AB=CD,
所以=,
所以=,
所以AC=BD.
9. (1) 证明:连接OC.
因为= ,
所以∠AOC=∠BOC.
又CD⊥OA,CE⊥OB,
所以CD=CE,
在△COD和△COE中,
所以△COD≌△COE(AAS),
所以OD=OE.
因为OA=OB,
所以AD=BE.
(2) 解:因为AD=DO,r=3,
所以AD=DO= .
又因为CD⊥OA,
所以在Rt△CDO中,CD===.
10. (1) 证明:因为∠AOB=∠COD,
所以=.
又因为= + ,= + ,
所以=.
(2) 解:因为=,
所以AC=BD=10.
因为OA=OC,E为AC的中点,
所以OE⊥AC,
所以AE=AC=5,
在Rt△AEO中,由勾股定理,得OE===,
所以OE的长是 .
11. C 12. A 13. 105° 14. 50°
15. (1) 证明:连接AE.
因为四边形ABCD是平行四边形,
所以AD∥BC,所以∠EAF=∠AEB,∠GAF=∠B.
因为AE=AB,所以∠B=∠AEB,
所以∠EAF=∠GAF,所以=.
(2) 解:因为的度数为140°,所以∠EAG=140°.
因为AE=AG,所以∠EGB=20°.
16. (1) 证明:如图1,连接AC,BD.
因为C,D是的三等分点,
所以==,
所以AC=CD=BD.
因为∠AOB=90°,
所以∠AOC=∠COD=∠BOD=30°.
因为OA=OB,
所以∠OAB=∠OBA=45°,
所以∠AEC=∠AOC+∠OAB=75°.
因为OA=OC,∠AOC=30°,
所以∠ACE=×(180°-30°)=75°=∠AEC,
所以AE=AC.
同理可得BF=BD,
所以AE=BF=CD.
(2) 解:成立.理由如下:
如图2,连接AC,BD.
因为C,D是的三等分点,
所以==,
所以AC=CD=BD.
因为∠AOB=120°,
所以∠AOC=∠COD=∠BOD=40°.
因为OA=OB,
所以∠OAB=∠OBA=30°,
所以∠AEC=∠AOC+∠OAB=70°.
因为OA=OC,∠AOC=40°,
所以∠ACE=×(180°-40°)=70°=∠AEC,
所以AE=AC.
同理可得BF=BD,
所以AE=BF=CD.
图1 图2
第2课时 垂径定理及推论
1. B 2. C 3. 9 4. 7 5. 16 6. a
7. (1) 证明:因为OE⊥AB,CD为⊙O的弦,
所以CF=DF.
因为OA=OB,OE⊥AB,
所以AF=BF,
所以AF-CF=BF-DF,
所以AC=BD.
(2) 解:如图,连接OC.
因为OE⊥AB,CD为⊙O的弦,
所以CF=CD=3,∠OFC=90°,
所以CO2=CF2+OF2.
设⊙O的半径是r,
则r2=32+(r-1)2,
解得r=5,
所以⊙O的半径是5.
8. B 9. 1或7 10. 2或4 11. (0,-4) 12. 6
13. 证明:如图,延长AD交⊙O于点E.
因为OC⊥AD,
所以=2,AE=2AD.
因为=2,
所以=,
所以AB=AE,所以AB=2AD.
14. 解:(1) 连接OA.
根据题意,得AD=AB=30 m,OD=(r-18)m.
在Rt△ADO中,由勾股定理,得r2=302+(r-18)2,
解得r=34.
故圆弧所在圆的半径r的长为34 m.
(2) 连接OA′.
因为OE=OP-PE=30 m,
所以在Rt△A′EO中,由勾股定理,得A′E2=A′O2-OE2,
解得A′E=16 m,所以A′B′=32 m.
因为A′B′=32 m>30 m,所以不需要采取紧急措施.
第1课时 圆心角、弧、弦之间的关系
1. 圆是中心对称图形,圆心是它的对称中心.
2. 圆心角、弧、弦之间的关系:
(1) 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;
(2) 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
3. 圆心角的度数与它所对的弧的度数相等.
建议用时:20分钟
1 下列说法中,正确的是( )
A. 等弦所对的弧相等 B. 等弧所对的弦相等
C. 圆心角相等,所对的弦相等 D. 相等的弦所对的圆心角相等
2 (2024苏州高新区月考)如图,A,B,C,D都是⊙O上的点,若CD=BD,∠AOC=108°,则∠AOD等于( )
A. 140° B. 144° C. 146° D. 150°
(第2题) (第3题) (第5题)
3 (2024南京期中)如图,点A,B,C,D都在⊙O上,OB⊥AC,BC=CD,则下列说法中错误的是( )
A. = B. ∠AOC=∠BOD C. AC=2CD D. OC⊥BD
4 已知⊙O的半径为12 cm,弦AB将圆分成的两段弧所对的圆心角度数之比为1∶5,则∠AOB的度数为________,弦AB的长为________cm.
5 如图,在Rt△ABC中,∠C=90°,∠A=26°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为________,的度数为________.
6 如图,正方形ABCD内接于⊙O,M为的中点,连接AM,BM.求证:=.
7 (2024连云港东海期中)如图,A,B,C,D是⊙O上的四个点,AD=BC.求证:AB=CD.
8 如图,在⊙O中,弦AB,CD相交于点E,且AB=CD.求证:AC=BD.
9 如图,在⊙O中,=,CD⊥AO于点D,CE⊥OB于点E.
(1) 求证:AD=BE;
(2) 若AD=DO,r=3,求CD的长.
10 如图,AC,BD是⊙O的弦,分别连接OA,OB,OC,OD,∠AOB=∠COD,AC与OB交于点E,⊙O的半径为6.
(1) 求证:=;
(2) 若BD=10,E为AC的中点,求OE的长.
建议用时:25+5分钟
11 (2024扬州宝应期中)如图,在⊙O中,点A,B,C在圆上,且弧AB的长等于弧AC长的2倍,则下列结论中正确的是( )
A. AB=2AC B. AB>2AC
C. AB<2AC D. 以上结论都不对
(第11题) (第12题) (第13题) (第14题)
12 如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为( )
A. 30° B. 40° C. 50° D. 60°
13 如图,已知C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是________.
14 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则的度数为________.
15 如图,以平行四边形ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于点E,F,交BA的延长线于点G,连接GE.
(1) 求证:=;
(2) 若的度数为140°,求∠EGB的度数.
16 (1) 如图1,在⊙O中,∠AOB=90°,且C,D是的三等分点,AB分别交OC,OD于点E,F.求证:AE=BF=CD;
(2) 在(1)中,如果∠AOB=120°,其他条件不变,如图2所示,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
图1 图2
第2课时 垂径定理及推论
1. 圆是轴对称图形,经过圆心的任意一条直线都是它的对称轴.
2. 垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧.
建议用时:20分钟
1 (2024长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为( )
A. 4 B. 4 C. 5 D. 5
(第1题) (第2题) (第3题) (第4题) (第5题)
2 如图,CD是⊙O的弦,AB是⊙O的直径,AB⊥CD,垂足为E,则下列结论中不一定成立的是( )
A. = B. = C. EO=EB D. EC=ED
3 (2024南京江宁月考)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5,CD=6,则AE=________.
4 如图,A,B,C是⊙O上的点,OC⊥AB于点D,且D为OC的中点,若OA=7,则BC的长为________.
5 如图,⊙O是一个盛有水的容器的纵截面,⊙O的半径为10 cm,水的最深处到水面AB的距离为4 cm,则水面AB的宽度为________ cm.
6 如图,A,B是⊙O上的两点,弦AB=a,P是⊙O上不与点A,B重合的一个动点,连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.(用含a的代数式表示)
7 (2024沛县期中)如图,OA=OB,AB交⊙O于点C,D,OE是半径,且OE⊥AB于点F.
(1) 求证:AC=BD;
(2) 若CD=6,EF=1,求⊙O的半径.
建议用时:25+5分钟
8 (2024通辽)如图,圆形拱门的最下端AB在地面上,D为AB的中点,C为拱门的最高点,线段CD经过拱门所在圆的圆心,若AB=1 m,CD=2.5 m,则拱门所在圆的半径为( )
A. 1.25 m B. 1.3 m C. 1.4 m D. 1.45 m
(第8题) (第11题) (第12题)
9 已知⊙O的半径为5,两条弦AB与CD平行,AB=6,CD=8,则AB与CD间的距离为________.
10 已知⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AC的长为________.
11 如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A,B,C,D四点.已知A(6,0),B(-2,0),C(0,3),则点D的坐标为________.
12 如图,在⊙O中,弦AB=6,点C在AB上移动,连接OC,过点C作DE⊥OC交⊙O于点D,E,则DE的最大值为________.
13 如图,在⊙O中,=2,AD⊥OC于点D.求证:AB=2AD.
14 如图,有一座拱桥的形状是圆弧形,它的跨度AB=60 m,拱高PD=18 m.
(1) 求圆弧所在圆的半径r的长;
(2) 当洪水泛滥到跨度只有30 m时,要采取紧急措施.若拱顶离水面只有4 m,即PE=4 m时,是否要采取紧急措施?
2.2 圆的对称性
第1课时 圆心角、弧、弦之间的关系
1. B 2. B 3. C 4. 60° 12 5. 52° 38°
6. 证明:因为四边形ABCD是正方形,
所以AD=BC,所以=.
因为M为的中点,所以=,
所以+=+,所以=.
7. 证明:因为AD=BC,
所以=,
所以+=+,
即=,
所以AB=CD.
8. 证明:因为AB=CD,
所以=,
所以=,
所以AC=BD.
9. (1) 证明:连接OC.
因为= ,
所以∠AOC=∠BOC.
又CD⊥OA,CE⊥OB,
所以CD=CE,
在△COD和△COE中,
所以△COD≌△COE(AAS),
所以OD=OE.
因为OA=OB,
所以AD=BE.
(2) 解:因为AD=DO,r=3,
所以AD=DO= .
又因为CD⊥OA,
所以在Rt△CDO中,CD===.
10. (1) 证明:因为∠AOB=∠COD,
所以=.
又因为= + ,= + ,
所以=.
(2) 解:因为=,
所以AC=BD=10.
因为OA=OC,E为AC的中点,
所以OE⊥AC,
所以AE=AC=5,
在Rt△AEO中,由勾股定理,得OE===,
所以OE的长是 .
11. C 12. A 13. 105° 14. 50°
15. (1) 证明:连接AE.
因为四边形ABCD是平行四边形,
所以AD∥BC,所以∠EAF=∠AEB,∠GAF=∠B.
因为AE=AB,所以∠B=∠AEB,
所以∠EAF=∠GAF,所以=.
(2) 解:因为的度数为140°,所以∠EAG=140°.
因为AE=AG,所以∠EGB=20°.
16. (1) 证明:如图1,连接AC,BD.
因为C,D是的三等分点,
所以==,
所以AC=CD=BD.
因为∠AOB=90°,
所以∠AOC=∠COD=∠BOD=30°.
因为OA=OB,
所以∠OAB=∠OBA=45°,
所以∠AEC=∠AOC+∠OAB=75°.
因为OA=OC,∠AOC=30°,
所以∠ACE=×(180°-30°)=75°=∠AEC,
所以AE=AC.
同理可得BF=BD,
所以AE=BF=CD.
(2) 解:成立.理由如下:
如图2,连接AC,BD.
因为C,D是的三等分点,
所以==,
所以AC=CD=BD.
因为∠AOB=120°,
所以∠AOC=∠COD=∠BOD=40°.
因为OA=OB,
所以∠OAB=∠OBA=30°,
所以∠AEC=∠AOC+∠OAB=70°.
因为OA=OC,∠AOC=40°,
所以∠ACE=×(180°-40°)=70°=∠AEC,
所以AE=AC.
同理可得BF=BD,
所以AE=BF=CD.
图1 图2
第2课时 垂径定理及推论
1. B 2. C 3. 9 4. 7 5. 16 6. a
7. (1) 证明:因为OE⊥AB,CD为⊙O的弦,
所以CF=DF.
因为OA=OB,OE⊥AB,
所以AF=BF,
所以AF-CF=BF-DF,
所以AC=BD.
(2) 解:如图,连接OC.
因为OE⊥AB,CD为⊙O的弦,
所以CF=CD=3,∠OFC=90°,
所以CO2=CF2+OF2.
设⊙O的半径是r,
则r2=32+(r-1)2,
解得r=5,
所以⊙O的半径是5.
8. B 9. 1或7 10. 2或4 11. (0,-4) 12. 6
13. 证明:如图,延长AD交⊙O于点E.
因为OC⊥AD,
所以=2,AE=2AD.
因为=2,
所以=,
所以AB=AE,所以AB=2AD.
14. 解:(1) 连接OA.
根据题意,得AD=AB=30 m,OD=(r-18)m.
在Rt△ADO中,由勾股定理,得r2=302+(r-18)2,
解得r=34.
故圆弧所在圆的半径r的长为34 m.
(2) 连接OA′.
因为OE=OP-PE=30 m,
所以在Rt△A′EO中,由勾股定理,得A′E2=A′O2-OE2,
解得A′E=16 m,所以A′B′=32 m.
因为A′B′=32 m>30 m,所以不需要采取紧急措施.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
