2.3 确定圆的条件 同步练 (含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 2.3 确定圆的条件 同步练 (含答案) 2025-2026学年数学苏科版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 00:00:00 | ||
图片预览

文档简介
2.3 确定圆的条件
1. 不在同一条直线上的三点确定一个圆.
2. 三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆;外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
3. 三角形的外心是三角形外接圆的圆心,是三角形三边的垂直平分线的交点,它到三个顶点的距离相等.
建议用时:20分钟
1 下列说法中,正确的是( )
A. 三个点确定一个圆
B. 一个圆有且只有一个内接三角形
C. 一个三角形有且只有一个外接圆
D. 三角形的外心到该三角形三边的距离相等
2 如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A. 3 B. 4 C. 5 D. 6
(第2题) (第3题) (第5题)
3 如图,在方格纸中,每个方格的边长为1,A,O两点都在格点上,在此方格纸格点上另外找两点B,C,使得△ABC的外心为O,则BC的长度为( )
A. 4 B. 5 C. D. 2
4 已知△ABC的三边长分别为5 cm,12 cm,13 cm,则这个三角形的外接圆的半径为________cm.
5 (2024宿迁沭阳月考)如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,若点A的坐标为(-1,-1),则△ABC的外心的坐标是________.
6 (2024南京建邺月考)若过平面直角坐标系中的三个点A(1,0),B(0,2),C(-1,m)能确定一个圆,则m的值不可能为________.
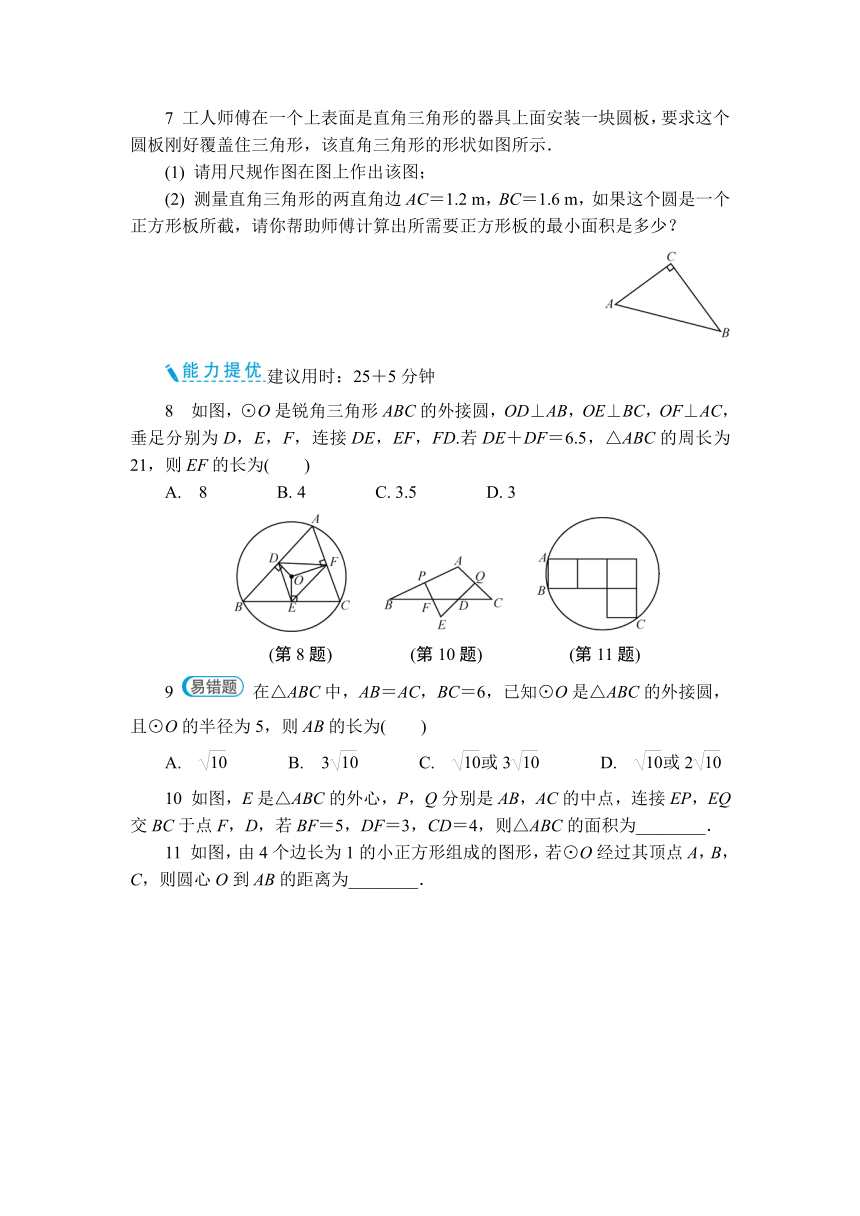
7 工人师傅在一个上表面是直角三角形的器具上面安装一块圆板,要求这个圆板刚好覆盖住三角形,该直角三角形的形状如图所示.
(1) 请用尺规作图在图上作出该图;
(2) 测量直角三角形的两直角边AC=1.2 m,BC=1.6 m,如果这个圆是一个正方形板所截,请你帮助师傅计算出所需要正方形板的最小面积是多少?
建议用时:25+5分钟
8 如图,⊙O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,连接DE,EF,FD.若DE+DF=6.5,△ABC的周长为21,则EF的长为( )
A. 8 B. 4 C. 3.5 D. 3
(第8题) (第10题) (第11题)
9 在△ABC中,AB=AC,BC=6,已知⊙O是△ABC的外接圆,且⊙O的半径为5,则AB的长为( )
A. B. 3 C. 或3 D. 或2
10 如图,E是△ABC的外心,P,Q分别是AB,AC的中点,连接EP,EQ交BC于点F,D,若BF=5,DF=3,CD=4,则△ABC的面积为________.
11 如图,由4个边长为1的小正方形组成的图形,若⊙O经过其顶点A,B,C,则圆心O到AB的距离为________.
12 如图,要把残破的图片恢复完整,已知弧上的三点A,B,C.
(1) 用尺规作图找出所在圆的圆心;
(2) 在△ABC中,若BC=8 cm,AB=AC=5 cm,求图片的半径r的长.
13 如图,在半径为8的⊙O中,弦AB=8,C是劣弧AB上的一个动点,D是弦AC的中点,E是弦BC的中点,P是半径OC的中点.
(1) 求∠AOB的度数,并说明点P为△ODE的外心;
(2) 当点C沿着劣弧AB从点A开始,逆时针运动到点B时,请直接写出△ODE面积的取值范围.
2.3 确定圆的条件
1. C 2. D 3. D 4. 5. (0,1) 6. 4
7. 解:(1) 作图如下:
(2) 因为AC=1.2 m,BC=1.6 m,∠ACB=90°,
所以AB===2(m),
所以所需要正方形板的最小面积是22=4(m2).
8. B 9. C 10. 24 11.
12. 解:(1) 分别作AB,AC的垂直平分线,交点即为圆心.
(2) 设圆的圆心为点O,连接AO交BC于点D.
易得D为BC的中点,且AD⊥BC,
则在Rt△ABD中,AB=5 cm,BD=BC=4 cm,
所以AD=3 cm.
连接BO,在Rt△BDO中,BO2=BD2+OD2,
即r2=42+(r-3)2,
解得r= cm,故图片的半径r为 cm.
13. 解:(1) 根据题意,得(8)2=82+82,
所以AB2=OA2+OB2,所以∠AOB=90°.
因为D是弦AC的中点,E是弦BC的中点,OA=OB=OC,
所以OD⊥AC,OE⊥BC,所以∠ODC=∠OEC=90°.
因为P是OC的中点,所以PD=PO=PE,
所以点P为△ODE的外心.
(2) 16<S△ODE≤8+8.
1. 不在同一条直线上的三点确定一个圆.
2. 三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆;外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
3. 三角形的外心是三角形外接圆的圆心,是三角形三边的垂直平分线的交点,它到三个顶点的距离相等.
建议用时:20分钟
1 下列说法中,正确的是( )
A. 三个点确定一个圆
B. 一个圆有且只有一个内接三角形
C. 一个三角形有且只有一个外接圆
D. 三角形的外心到该三角形三边的距离相等
2 如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A. 3 B. 4 C. 5 D. 6
(第2题) (第3题) (第5题)
3 如图,在方格纸中,每个方格的边长为1,A,O两点都在格点上,在此方格纸格点上另外找两点B,C,使得△ABC的外心为O,则BC的长度为( )
A. 4 B. 5 C. D. 2
4 已知△ABC的三边长分别为5 cm,12 cm,13 cm,则这个三角形的外接圆的半径为________cm.
5 (2024宿迁沭阳月考)如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,若点A的坐标为(-1,-1),则△ABC的外心的坐标是________.
6 (2024南京建邺月考)若过平面直角坐标系中的三个点A(1,0),B(0,2),C(-1,m)能确定一个圆,则m的值不可能为________.
7 工人师傅在一个上表面是直角三角形的器具上面安装一块圆板,要求这个圆板刚好覆盖住三角形,该直角三角形的形状如图所示.
(1) 请用尺规作图在图上作出该图;
(2) 测量直角三角形的两直角边AC=1.2 m,BC=1.6 m,如果这个圆是一个正方形板所截,请你帮助师傅计算出所需要正方形板的最小面积是多少?
建议用时:25+5分钟
8 如图,⊙O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,连接DE,EF,FD.若DE+DF=6.5,△ABC的周长为21,则EF的长为( )
A. 8 B. 4 C. 3.5 D. 3
(第8题) (第10题) (第11题)
9 在△ABC中,AB=AC,BC=6,已知⊙O是△ABC的外接圆,且⊙O的半径为5,则AB的长为( )
A. B. 3 C. 或3 D. 或2
10 如图,E是△ABC的外心,P,Q分别是AB,AC的中点,连接EP,EQ交BC于点F,D,若BF=5,DF=3,CD=4,则△ABC的面积为________.
11 如图,由4个边长为1的小正方形组成的图形,若⊙O经过其顶点A,B,C,则圆心O到AB的距离为________.
12 如图,要把残破的图片恢复完整,已知弧上的三点A,B,C.
(1) 用尺规作图找出所在圆的圆心;
(2) 在△ABC中,若BC=8 cm,AB=AC=5 cm,求图片的半径r的长.
13 如图,在半径为8的⊙O中,弦AB=8,C是劣弧AB上的一个动点,D是弦AC的中点,E是弦BC的中点,P是半径OC的中点.
(1) 求∠AOB的度数,并说明点P为△ODE的外心;
(2) 当点C沿着劣弧AB从点A开始,逆时针运动到点B时,请直接写出△ODE面积的取值范围.
2.3 确定圆的条件
1. C 2. D 3. D 4. 5. (0,1) 6. 4
7. 解:(1) 作图如下:
(2) 因为AC=1.2 m,BC=1.6 m,∠ACB=90°,
所以AB===2(m),
所以所需要正方形板的最小面积是22=4(m2).
8. B 9. C 10. 24 11.
12. 解:(1) 分别作AB,AC的垂直平分线,交点即为圆心.
(2) 设圆的圆心为点O,连接AO交BC于点D.
易得D为BC的中点,且AD⊥BC,
则在Rt△ABD中,AB=5 cm,BD=BC=4 cm,
所以AD=3 cm.
连接BO,在Rt△BDO中,BO2=BD2+OD2,
即r2=42+(r-3)2,
解得r= cm,故图片的半径r为 cm.
13. 解:(1) 根据题意,得(8)2=82+82,
所以AB2=OA2+OB2,所以∠AOB=90°.
因为D是弦AC的中点,E是弦BC的中点,OA=OB=OC,
所以OD⊥AC,OE⊥BC,所以∠ODC=∠OEC=90°.
因为P是OC的中点,所以PD=PO=PE,
所以点P为△ODE的外心.
(2) 16<S△ODE≤8+8.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
